Exam 12: Simple Linear Regression and Correlation

A procedure used to estimate the regression parameters $\beta _ { 1 } \text { and } \beta _ { 2 }$ and to find the least squares line which provides the best approximation for the relationship between the explanatory variable x and the response variable Y is known as the

Which of the following statements are not true?

Which of the following statements are true?

If $S _ { x ,y } = - 289.17 \text { and } S _ { xx} = 340.2 \text {, }$ then the least squares estimate of the slope coefficient $\beta _ { 1 }$ of the true regression line $y = \beta _ { 0 } + \beta _ { 1 } x \text { is } \hat { \beta } _ { 1 }$ = __________.

Which of the following statements are true?

If the $100 ( 1 - \alpha ) \%$ confidence interval $\left( \hat { \beta } _ { 0 } + \hat { \beta } _ { 1 } x ^ { + } \right) \pm t _ { \alpha/2 , n - 2 }$ . For the expected value of Y when $x = x ^ { +}$ is computed both for x = a and for x = b to obtain joint confidence intervals for 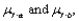then the joint confidence coefficient on the resulting pair of intervals is at least __________ %.

The accompanying data was read from a graph that appeared in a recent study. The independent variable is $\mathrm { SO } _ { 2 } \text { deposition rate } \left( \mathrm { mg } / \mathrm { m } ^ { 2 } / \right. \text { day) }$ and the dependent variable is steel weight loss (g/m $2$ ). x 14 18 40 43 45 112 y 280 350 470 500 560 1200 a. Construct a scatter plot. Does the simple linear regression model appear to be reasonable in this situation? b. Calculate the equation of the estimated regression line. c. What percentage of observed variation in steel weight loss can be attributed to the model relationship in combination with variation in deposition rate? d. Because the largest x value in the sample greatly exceeds the others, this observation may have been very influential in determining the equation of the estimated line. Delete this observation and recalculate the equation. Does the new equation appear to differ substantially from the original one (you might consider predicted values)?

A sample of n = 10,000 (x, y) pairs resulted in r = .022. Test $H _ { o } : \rho = 0 \text { versus } H _ { \pm} : \rho \neq 0$ at level .05. Is the result statistically significant? Comment on the practical significance of your analysis.

In the simple linear regression model $Y = \beta _ { 0 } + \beta _ { 1 } x + E ,$ the quantity E is a random variable, assumed to be normally distributed with E( $\varepsilon$ ) = 0 and V( $\varepsilon$ ) = $\sigma ^ { 2}$ . The estimator $\hat { \beta } _ { 1 }$ has a __________ distribution, because it is a linear function of independent __________ random variables.

If $\sum \left( x _ { i} - \bar { x } \right) \left( y _ { i } - \bar { y } \right) = 128 \text { and } \sum \left( x _ { i } - \bar { x } \right) ^ { 2 } = 80$ then the least squares estimate of the slope coefficient $\beta _ { 1 }$ of the true regression line $y = \beta _ { 0 } + \beta _ { 1 } x$ is

Which of the following statements are not true?

In a simple linear regression, the most commonly encountered pair of hypotheses about $\beta _ { 1 }$ is $H _ { 0 } : \beta _ { 1 } = 0 \text { versus } H _ { \pm} : \beta _ { 1 } \pm 0 \text {. }$ A test of these two hypotheses is often referred to as the __________.

Which of the following statements are true?

The principle of least squares results in values of $\hat { \beta } _ { 0 } \text { and } \hat { \beta } _ { 1 }$ that minimizes the sum of squared deviations between

Which of the following statements are true?

The t critical value for a confidence level of 90% for the slope $\beta _ { 1 }$ of the regression line, based on a sample of size 20, is t = __________.

A study reports the results of a regression analysis based on n = 15 observations in which x = filter application temperature ( $\degree$ C) and y = % efficiency of BOD removal. Calculated quantities include $\sum x _ { 1 } = 402 , \sum x _ { l } ^ { 2 } = 11,098 , s = 3.725 , \text { and } \hat { \beta } _ { 1 } = 1.7035$ a. Test at level .01 $H _ { 0 } : \beta _ { 1 } = 1$ which states that the expected increase in % BOD removal is 1 when filter application temperature increases by 1 $\degree$ C, against the alternative $H _ { \pm } : \beta _ { 1 } > 1$ b. Compute a 99% CI for $\beta _ { 1 } ,$ the expected increase in % BOD removal for a 1 $\degree$ C increase in filter application temperature.

The Turbine Oil Oxidation Test (TOST) and the Rotating Bomb Oxidation Test (RBOT) are two different procedures for evaluating the oxidation stability of steam turbine oils. The accompanying observations on x = TOST time (hr) and y = RBOT time (min) for 12 oil specimens have been reported: TOST 4200 3600 3750 3675 4050 2770 RBOT 370 340 375 310 350 200 TOST 4870 4500 3450 2700 3750 3300 RBOT 400 375 285 225 345 285 a. Calculate and interpret the value of the sample correlation coefficient . b. How would the value of r be affected if we had let x = RBOT time and y = TOST time? c. How would the value of r be affected if RBOT time were expressed in hours? d. Normal probability plots indicate that Both TOST and ROBT time appear to have come from normally distributed populations. Carry out a test of hypotheses to decide whether RBOT time and TOST time are linearly related.

Which of the above statements are not true?

Which of the following statements are true?