Deck 14: Markov Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/103
Play
Full screen (f)
Deck 14: Markov Analysis
1
For any absorbing state, the probability that a state will remain unchanged in the future is one.
True
2
In Markov analysis, the row elements of the transition matrix must sum to 1.
True
3
Once a Markov process is in equilibrium, it stays in equilibrium.
True
4
Markov analysis assumes that while a member of one state may move to a different state over time, the overall makeup of the system will remain the same.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
5
In Markov analysis it is assumed that states are both mutually exclusive and collectively exhaustive.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
6
(n + 1)= nP

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
7
Markov analysis assumes that there are a limited number of states in the system.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
8
Equilibrium state probabilities may be estimated by using Markov analysis for a large number of periods.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
9
In Markov analysis, initial-state probability values determine equilibrium conditions.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
10
In Markov analysis, the transition probability Pij represents the conditional probability of being in state i in the future given the current state of j.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
11
Creating the fundamental matrix requires a partition of the matrix of transition.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
12
An equilibrium condition exists if the state probabilities for a future period are the same as the state probabilities for a previous period.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
13
The vector of state probabilities gives the probability of being in particular states at a particular point in time.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
14
Markov analysis is a technique that deals with the probabilities of future occurrences by analyzing currently known probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
15
The probabilities in any column of the matrix of transition probabilities will always sum to one.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
16
The vector of state probabilities for any period is equal to the vector of state probabilities for the preceding period multiplied by the matrix of transition probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
17
When absorbing states exist, the fundamental matrix is used to compute equilibrium conditions.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
18
The four basic assumptions of Markov analysis are:
There are a limited or finite number of possible states.
The probability of changing states remains the same over time.
A future state is predictable from previous state and transition matrix.
The size and makeup of the system are constant during analysis.
There are a limited or finite number of possible states.
The probability of changing states remains the same over time.
A future state is predictable from previous state and transition matrix.
The size and makeup of the system are constant during analysis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
19
"Events" are used to identify all possible conditions of a process or a system.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
20
In the matrix of transition probabilities, Pij is the conditional probability of being in state i in the future, given the current state j.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
21
In Markov analysis, the vector of state probabilities represents the market shares.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
22
One of the purposes of Markov analysis is to predict the future.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
23
One of the problems with using the Markov model to study population shifts is that we must assume that the reasons for moving from one state to another remain the same over time.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
24
A matrix of transition probabilities is of dimension Pmn.The vector of current market share must be of dimension πm1.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
25
The matrix of transition probabilities gives the conditional probabilities of moving from one state to another.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
26
Occasionally, a state is entered that will not allow going to any other state in the future.This is called
A)stability dependency.
B)market saturation.
C)incidental mobility.
D)an absorbing state.
A)stability dependency.
B)market saturation.
C)incidental mobility.
D)an absorbing state.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
27
A collection of all state probabilities for a given system at any given period of time is called the
A)transition probabilities.
B)vector of state probabilities.
C)fundamental matrix.
D)equilibrium condition.
A)transition probabilities.
B)vector of state probabilities.
C)fundamental matrix.
D)equilibrium condition.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
28
If we are in any period n, we can compute the state probabilities for period n + 1 as π(n + 1)= π(n)P

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
29
In Markov analysis, we also assume that the states are
A)collectively exhaustive.
B)mutually exclusive.
C)independent.
D)Both collectively exhaustive and mutually exclusive.
A)collectively exhaustive.
B)mutually exclusive.
C)independent.
D)Both collectively exhaustive and mutually exclusive.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
30
Markov analysis is a technique that deals with the probabilities of future occurrences by
A)using the simplex solution method.
B)analyzing currently known probabilities.
C)statistical sampling.
D)the minimal spanning tree.
A)using the simplex solution method.
B)analyzing currently known probabilities.
C)statistical sampling.
D)the minimal spanning tree.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
31
A Markov process could be used as a model of how a disease progresses from one set of symptoms to another.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
32
In Markov analysis, the likelihood that any system will change from one period to the next is revealed by the
A)cross-elasticities.
B)fundamental matrix.
C)matrix of transition probabilities.
D)vector of state probabilities.
A)cross-elasticities.
B)fundamental matrix.
C)matrix of transition probabilities.
D)vector of state probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
33
In a matrix of transition probabilities
A)the probabilities for any column will sum to 1.
B)the probabilities for any row will sum to 1.
C)the probabilities for any column are mutually exclusive and collectively exhaustive.
D)the probabilities of all columns will sum to 1.
A)the probabilities for any column will sum to 1.
B)the probabilities for any row will sum to 1.
C)the probabilities for any column are mutually exclusive and collectively exhaustive.
D)the probabilities of all columns will sum to 1.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
34
A state probability when equilibrium has been reached is called
A)state probability.
B)prior probability.
C)steady state probability.
D)joint probability.
A)state probability.
B)prior probability.
C)steady state probability.
D)joint probability.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
35
In a tree diagram, the numbers associated with the arcs moving from one state to the next would be represented in the matrix of transition probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
36
The probability that we will be in a future state, given a current or existing state, is called
A)state probability.
B)prior probability.
C)steady state probability.
D)transition probability.
A)state probability.
B)prior probability.
C)steady state probability.
D)transition probability.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
37
The state probabilities for n periods in the future can be obtained from the current state probabilities and the matrix of equilibrium probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
38
Collectively exhaustive means that a system can be in only one state at any point in time.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
39
If you are in an absorbing state, you cannot go to another state in the future.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following is not an assumption of Markov processes?
A)The state variable is discrete.
B)There are a limited number of possible states.
C)The probability of changing states remains the same over time.
D)We can predict any future state from the previous state and the matrix of transition probabilities.
A)The state variable is discrete.
B)There are a limited number of possible states.
C)The probability of changing states remains the same over time.
D)We can predict any future state from the previous state and the matrix of transition probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
41
The copy machine in an office is very unreliable.If it was working yesterday, there is an 80% chance it will work today.If it was not working yesterday, there is a 10% chance it will work today.If it is not working today, what is the probability that it will be working 2 days from now?
A)0.16
B)0.17
C)0.34
D)0.66
A)0.16
B)0.17
C)0.34
D)0.66

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
42
The initial values for the state probabilities
A)are always greater than the equilibrium state probabilities.
B)are always less than the equilibrium state probabilities.
C)do not influence the equilibrium state probabilities.
D)heavily influence the equilibrium state probabilities.
A)are always greater than the equilibrium state probabilities.
B)are always less than the equilibrium state probabilities.
C)do not influence the equilibrium state probabilities.
D)heavily influence the equilibrium state probabilities.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
43
What do we do when solving for equilibrium conditions?
A)conduct a statistical t-test
B)drop one equation
C)partition the matrix of transition probabilities
D)subtract matrix B from the identity matrix
A)conduct a statistical t-test
B)drop one equation
C)partition the matrix of transition probabilities
D)subtract matrix B from the identity matrix

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
44
If we want to use Markov analysis to study market shares for competitive businesses
A)it is an inappropriate study.
B)simply replace the probabilities with market shares.
C)it can only accommodate one new business each period.
D)only constant changes in the matrix of transition probabilities can be handled in the simple model.
A)it is an inappropriate study.
B)simply replace the probabilities with market shares.
C)it can only accommodate one new business each period.
D)only constant changes in the matrix of transition probabilities can be handled in the simple model.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
45
The weather is becoming important to you since you would like to go on a picnic today.If it was sunny yesterday, there is a 70% chance it will be sunny today.If it was raining yesterday, there is a 30% chance it will be sunny today.What is the probability it will be rainy today, if it was sunny yesterday?
A)0.1
B)0.2
C)0.3
D)0.4
A)0.1
B)0.2
C)0.3
D)0.4

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
46
The copy machine in an office is very unreliable.If it was working yesterday, there is an 80% chance it will work today.If it was not working yesterday, there is a 10% chance it will work today.If it is working today, what is the probability that it will be working 2 days from now?
A)0.16
B)0.64
C)0.66
D)0.80
A)0.16
B)0.64
C)0.66
D)0.80

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
47
Table 14-1
The following data consists of a matrix of transition probabilities (P)of three competing companies, and the initial market share π(0).Assume that each state represents a company (Company 1, Company 2, Company 3, respectively)and the transition probabilities represent changes from one month to the next.
P = π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)
Using the data in Table 14-1, and assuming that the transition probabilities do not change, in the long run what market share would Company 2 expect to reach? (Rounded to two decimal places.)
A)0.30
B)0.32
C)0.39
D)0.60
The following data consists of a matrix of transition probabilities (P)of three competing companies, and the initial market share π(0).Assume that each state represents a company (Company 1, Company 2, Company 3, respectively)and the transition probabilities represent changes from one month to the next.
P =
 π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)Using the data in Table 14-1, and assuming that the transition probabilities do not change, in the long run what market share would Company 2 expect to reach? (Rounded to two decimal places.)
A)0.30
B)0.32
C)0.39
D)0.60

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
48
In Markov analysis, to find the vector of state probabilities for any period
A)one should find them empirically.
B)subtract the product of the numbers on the primary diagonal from the product of the numbers on the secondary diagonal.
C)find the product of the vector of state probabilities for the preceding period and the matrix of transition probabilities.
D)find the product of the vectors of state probabilities for the two preceding periods.
A)one should find them empirically.
B)subtract the product of the numbers on the primary diagonal from the product of the numbers on the secondary diagonal.
C)find the product of the vector of state probabilities for the preceding period and the matrix of transition probabilities.
D)find the product of the vectors of state probabilities for the two preceding periods.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
49
In a(n)________ state, you cannot go to another state in the future.
A)transition
B)equilibrium
C)locked
D)absorbing
A)transition
B)equilibrium
C)locked
D)absorbing

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
50
The matrix that is needed to compute equilibrium conditions when absorbing states are involved is called a(n)
A)transition matrix.
B)fundamental matrix.
C)equilibrium matrix.
D)absorbing matrix.
A)transition matrix.
B)fundamental matrix.
C)equilibrium matrix.
D)absorbing matrix.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
51
If in an absorbing state, the probability of being in an absorbing state in the future is
A)25%.
B)50%.
C)75%.
D)100%.
A)25%.
B)50%.
C)75%.
D)100%.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
52
To find the equilibrium state in Markov analysis
A)it is necessary to know both the vector of state probabilities and the matrix of transition probabilities.
B)it is necessary only to know the matrix of transition probabilities.
C)it is necessary only to know the vector of state probabilities for the initial period.
D)one should develop a table of state probabilities over time and then determine the equilibrium conditions empirically.
A)it is necessary to know both the vector of state probabilities and the matrix of transition probabilities.
B)it is necessary only to know the matrix of transition probabilities.
C)it is necessary only to know the vector of state probabilities for the initial period.
D)one should develop a table of state probabilities over time and then determine the equilibrium conditions empirically.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
53
At equilibrium
A)state probabilities for the next period equal the state probabilities for this period.
B)the state probabilities are all equal to each other.
C)the matrix of transition probabilities is symmetrical.
D)the vector of state probabilities is symmetrical.
A)state probabilities for the next period equal the state probabilities for this period.
B)the state probabilities are all equal to each other.
C)the matrix of transition probabilities is symmetrical.
D)the vector of state probabilities is symmetrical.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
54
Where P is the matrix of transition probabilities, π(4)=
A)π(3)P P P.
B)π(3)P P.
C)π(2)P P P.
D)π(1)P P P.
A)π(3)P P P.
B)π(3)P P.
C)π(2)P P P.
D)π(1)P P P.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
55
Table 14-1
The following data consists of a matrix of transition probabilities (P)of three competing companies, and the initial market share π(0).Assume that each state represents a company (Company 1, Company 2, Company 3, respectively)and the transition probabilities represent changes from one month to the next.
P = π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)
Using the data in Table 14-1, determine Company 2's estimated market share in the next period.
A)0.26
B)0.27
C)0.28
D)0.29
The following data consists of a matrix of transition probabilities (P)of three competing companies, and the initial market share π(0).Assume that each state represents a company (Company 1, Company 2, Company 3, respectively)and the transition probabilities represent changes from one month to the next.
P =
 π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)Using the data in Table 14-1, determine Company 2's estimated market share in the next period.
A)0.26
B)0.27
C)0.28
D)0.29

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
56
The weather is becoming important to you since you would like to go on a picnic today.If it was sunny yesterday, there is a 70% chance it will be sunny today.If it was raining yesterday, there is a 30% chance it will be sunny today.If the probability that it was raining yesterday is 0.25, what is the probability that it will rain today?
A)0.1
B)0.3
C)0.4
D)0.7
A)0.1
B)0.3
C)0.4
D)0.7

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
57
Table 14-1
The following data consists of a matrix of transition probabilities (P)of three competing companies, and the initial market share π(0).Assume that each state represents a company (Company 1, Company 2, Company 3, respectively)and the transition probabilities represent changes from one month to the next.
P = π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)
Using the data in Table 14-1, determine Company 1's estimated market share in the next period.
A)0.10
B)0.20
C)0.42
D)0.47
The following data consists of a matrix of transition probabilities (P)of three competing companies, and the initial market share π(0).Assume that each state represents a company (Company 1, Company 2, Company 3, respectively)and the transition probabilities represent changes from one month to the next.
P =
 π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)Using the data in Table 14-1, determine Company 1's estimated market share in the next period.
A)0.10
B)0.20
C)0.42
D)0.47

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
58
The weather is becoming important to you since you would like to go on a picnic today.If it was sunny yesterday, there is a 65% chance it will be sunny today.If it was raining yesterday, there is a 30% chance it will be sunny today.If the probability that it was raining yesterday is 0.4, what is the probability that it will be sunny today?
A)0.650
B)0.390
C)0.510
D)0.490
A)0.650
B)0.390
C)0.510
D)0.490

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
59
A state that when entered, cannot be left is called
A)transient.
B)recurrent.
C)absorbing.
D)steady.
A)transient.
B)recurrent.
C)absorbing.
D)steady.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
60
In the long run, in Markov analysis
A)all state probabilities will eventually become zeros or ones.
B)generally, the vector of state probabilities, when multiplied by the matrix of transition probabilities, will yield the same vector of state probabilities.
C)the matrix of transition probabilities will change to an equilibrium state.
D)the matrices will become inverted.
A)all state probabilities will eventually become zeros or ones.
B)generally, the vector of state probabilities, when multiplied by the matrix of transition probabilities, will yield the same vector of state probabilities.
C)the matrix of transition probabilities will change to an equilibrium state.
D)the matrices will become inverted.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
61
Table 14-4
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).</strong> A)126 B)95 C)79 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).</strong> A)126 B)95 C)79 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).
A)126
B)95
C)79
D)100
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).</strong> A)126 B)95 C)79 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).</strong> A)126 B)95 C)79 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).
A)126
B)95
C)79
D)100

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
62
Table 14-4
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many people can we expect to find in each city tomorrow evening?</strong> A)Chaos = 90, Frenzy = 110, Tremor = 100 B)Chaos = 110, Frenzy = 100, Tremor = 90 C)Chaos = 80, Frenzy = 90, Tremor = 130 D)Chaos = 100, Frenzy = 130, Tremor = 70](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many people can we expect to find in each city tomorrow evening?</strong> A)Chaos = 90, Frenzy = 110, Tremor = 100 B)Chaos = 110, Frenzy = 100, Tremor = 90 C)Chaos = 80, Frenzy = 90, Tremor = 130 D)Chaos = 100, Frenzy = 130, Tremor = 70](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, how many people can we expect to find in each city tomorrow evening?
A)Chaos = 90, Frenzy = 110, Tremor = 100
B)Chaos = 110, Frenzy = 100, Tremor = 90
C)Chaos = 80, Frenzy = 90, Tremor = 130
D)Chaos = 100, Frenzy = 130, Tremor = 70
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many people can we expect to find in each city tomorrow evening?</strong> A)Chaos = 90, Frenzy = 110, Tremor = 100 B)Chaos = 110, Frenzy = 100, Tremor = 90 C)Chaos = 80, Frenzy = 90, Tremor = 130 D)Chaos = 100, Frenzy = 130, Tremor = 70](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many people can we expect to find in each city tomorrow evening?</strong> A)Chaos = 90, Frenzy = 110, Tremor = 100 B)Chaos = 110, Frenzy = 100, Tremor = 90 C)Chaos = 80, Frenzy = 90, Tremor = 130 D)Chaos = 100, Frenzy = 130, Tremor = 70](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, how many people can we expect to find in each city tomorrow evening?
A)Chaos = 90, Frenzy = 110, Tremor = 100
B)Chaos = 110, Frenzy = 100, Tremor = 90
C)Chaos = 80, Frenzy = 90, Tremor = 130
D)Chaos = 100, Frenzy = 130, Tremor = 70

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
63
Table 14-5
The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next.
P =

π(0)= (.3, .3, .4)
Using the data in Table 14-5, determine Disease 1's estimated incidence in the next period.
A)0.32
B)0.34
C)0.36
D)0.38
The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next.
P =

π(0)= (.3, .3, .4)
Using the data in Table 14-5, determine Disease 1's estimated incidence in the next period.
A)0.32
B)0.34
C)0.36
D)0.38

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
64
Table 14-6
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, which major will end up with the greatest proportion of students?
A)Major 1
B)Major 2
C)Major 3
D)Major 4
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, which major will end up with the greatest proportion of students?
A)Major 1
B)Major 2
C)Major 3
D)Major 4

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
65
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =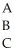
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)
Using the data given in Table 14-3, how many employees do we expect in location B one year from now?
A)1000
B)1400
C)1500
D)800
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =
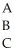
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)Using the data given in Table 14-3, how many employees do we expect in location B one year from now?
A)1000
B)1400
C)1500
D)800

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
66
Table 14-2
The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next.
P = π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)
Using the data given in Table 14-2, what is the equilibrium market share?
A)(0.55, 0.33, 0.12)
B)(0.44, 0.43, 0.12
C)(0.55, 0.12, 0.33)
D)(0.47, 0.40, 0.13)
The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next.
P =
 π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)Using the data given in Table 14-2, what is the equilibrium market share?
A)(0.55, 0.33, 0.12)
B)(0.44, 0.43, 0.12
C)(0.55, 0.12, 0.33)
D)(0.47, 0.40, 0.13)

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
67
Table 14-5
The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next.
P =

π(0)= (.3, .3, .4)
Using the data in Table 14-5, which disease will have the highest incidence when absorbing states are reached?
A)Disease 1
B)Disease 2
C)Disease 3
D)Disease 1 and Disease 3 are tied for the highest incidence
The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next.
P =

π(0)= (.3, .3, .4)
Using the data in Table 14-5, which disease will have the highest incidence when absorbing states are reached?
A)Disease 1
B)Disease 2
C)Disease 3
D)Disease 1 and Disease 3 are tied for the highest incidence

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
68
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =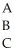
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)
Using the data given in Table 14-3, how many employees do we expect in location B two years from now?
A)1420
B)1400
C)10090
D)820
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =
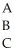
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)Using the data given in Table 14-3, how many employees do we expect in location B two years from now?
A)1420
B)1400
C)10090
D)820

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
69
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =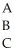
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)
Using the data given in Table 14-3, how many employees do we expect in location A one year from now?
A)1000
B)1400
C)1500
D)800
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =
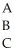
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)Using the data given in Table 14-3, how many employees do we expect in location A one year from now?
A)1000
B)1400
C)1500
D)800

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
70
Table 14-6
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 1's estimated popularity after students have taken the first introductory course.
A)0.425
B)0.385
C)0.365
D)0.415
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 1's estimated popularity after students have taken the first introductory course.
A)0.425
B)0.385
C)0.365
D)0.415

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
71
Table 14-2
The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next.
P = π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)
Using the data given in Table 14-2, find the market shares for the three retailers in month 1.
A)π(1)= (0.09, 0.42, 0.49)
B)π(1)= (0.55, 0.33, 0.12)
C)π(1)= (0.18, 0.12, 0.70)
D)π(1)= (0.55, 0.12, 0.33)
The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next.
P =
 π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)Using the data given in Table 14-2, find the market shares for the three retailers in month 1.
A)π(1)= (0.09, 0.42, 0.49)
B)π(1)= (0.55, 0.33, 0.12)
C)π(1)= (0.18, 0.12, 0.70)
D)π(1)= (0.55, 0.12, 0.33)

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
72
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =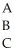
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)
Using the data given in Table 14-3, what is the long run number of employees expected in location C?
A)1400
B)1000
C)800
D)750
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =
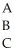
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)Using the data given in Table 14-3, what is the long run number of employees expected in location C?
A)1400
B)1000
C)800
D)750

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
73
Table 14-5
The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next.
P =

π(0)= (.3, .3, .4)
Using the data in Table 14-5, determine Disease 3's estimated incidence in the next period.
A)0.32
B)0.34
C)0.36
D)0.38
The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next.
P =

π(0)= (.3, .3, .4)
Using the data in Table 14-5, determine Disease 3's estimated incidence in the next period.
A)0.32
B)0.34
C)0.36
D)0.38

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
74
Table 14-4
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many seats should Cuthbert schedule for travel from Chaos to Frenzy for tomorrow?</strong> A)110 B)100 C)90 D)80](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many seats should Cuthbert schedule for travel from Chaos to Frenzy for tomorrow?</strong> A)110 B)100 C)90 D)80](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, how many seats should Cuthbert schedule for travel from Chaos to Frenzy for tomorrow?
A)110
B)100
C)90
D)80
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many seats should Cuthbert schedule for travel from Chaos to Frenzy for tomorrow?</strong> A)110 B)100 C)90 D)80](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, how many seats should Cuthbert schedule for travel from Chaos to Frenzy for tomorrow?</strong> A)110 B)100 C)90 D)80](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, how many seats should Cuthbert schedule for travel from Chaos to Frenzy for tomorrow?
A)110
B)100
C)90
D)80

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
75
Table 14-6
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 3's estimated popularity after students have taken the first two introductory courses.
A)0.232
B)0.220
C)0.356
D)0.191
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 3's estimated popularity after students have taken the first two introductory courses.
A)0.232
B)0.220
C)0.356
D)0.191

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
76
Table 14-2
The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next.
P = π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)
Using the data given in Table 14-2, find the market shares for the three retailers in month 2.
A)π(2)= (0.30, 0.60, 0.10)
B)π(2)= (0.55, 0.33, 0.12)
C)π(2)= (0.44, 0.43, 0.12)
D)π(2)= (0.55, 0.12, 0.33)
The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next.
P =
 π(0)= (0.3, 0.6, 0.1)
π(0)= (0.3, 0.6, 0.1)Using the data given in Table 14-2, find the market shares for the three retailers in month 2.
A)π(2)= (0.30, 0.60, 0.10)
B)π(2)= (0.55, 0.33, 0.12)
C)π(2)= (0.44, 0.43, 0.12)
D)π(2)= (0.55, 0.12, 0.33)

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
77
Table 14-4
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?</strong> A)79 B)95 C)126 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?</strong> A)79 B)95 C)126 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?
A)79
B)95
C)126
D)100
Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis.
C F T
Transition matrix:
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?</strong> A)79 B)95 C)126 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5265_b53a_594c8c547055_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
![<strong>Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?</strong> A)79 B)95 C)126 D)100](https://storage.examlex.com/TB5481/11eab9ea_e5cc_5266_b53a_3ba57bc18d64_TB5481_11_TB5481_11_TB5481_11_TB5481_11.jpg)
π(0)= [100, 100, 100]
Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?
A)79
B)95
C)126
D)100

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
78
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =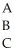
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)
Using the data given in Table 14-3, how many employees do we expect in location A two years from now?
A)1000
B)1400
C)1420
D)1500
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P =
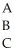
 π(0)= [1000, 1000, 1000)
π(0)= [1000, 1000, 1000)Using the data given in Table 14-3, how many employees do we expect in location A two years from now?
A)1000
B)1400
C)1420
D)1500

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
79
Table 14-6
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 4's estimated popularity after students have taken the first two introductory courses.
A)0.232
B)0.220
C)0.356
D)0.191
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 4's estimated popularity after students have taken the first two introductory courses.
A)0.232
B)0.220
C)0.356
D)0.191

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
80
Table 14-6
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 2's estimated popularity after students have taken the first introductory course.
A)0.225
B)0.305
C)0.245
D)0.205
The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline.
P =

π(0)= (.4, .3, .2, .1)
Using the data in Table 14-6, determine Major 2's estimated popularity after students have taken the first introductory course.
A)0.225
B)0.305
C)0.245
D)0.205

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck


