Deck 5: Linear Regression As a Fundamental Descriptive Tool
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/53
Play
Full screen (f)
Deck 5: Linear Regression As a Fundamental Descriptive Tool
1
If one was estimating a simple regression of Earnings (Y) on Height of individuals (X), and got a coefficient on the Height variable of 30, what would the coefficient on Height be if you added 3 inches to every individual in the sample but kept their earnings the same?
A) 30
B) Above 30
C) Below 30
D) Not enough information.
A) 30
B) Above 30
C) Below 30
D) Not enough information.
A
2
For the simple linear regression, Y = b + mX, which variable is considered the intercept?
A) Y
B) b
C) m
D) X
A) Y
B) b
C) m
D) X
B
3
In a dichotomous regression all of the following conditions must hold except for what?
A) The sum of residuals for the treated group must equal zero.
B) The sum of residuals for the untreated group must equal zero.
C) An equal number of positive and negative residuals.
D) The regression line must go through the mean of the outcomes for the treated.
A) The sum of residuals for the treated group must equal zero.
B) The sum of residuals for the untreated group must equal zero.
C) An equal number of positive and negative residuals.
D) The regression line must go through the mean of the outcomes for the treated.
C
4
How many regression parameters will be estimated in a simple linear regression model?
A) 1
B) 2
C) 3
D) 1 + number of observations
A) 1
B) 2
C) 3
D) 1 + number of observations

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
5
If we wish to use a regression line to determine the effect of multiple treatment levels , why can't we just plot the average outcome for each treatment level and "connect the dots?"
A) Connecting the dots generally will not form a line.
B) Using averages for each treatment level will generally create bias.
C) This will cause us to have too few equations to solve for our unknown parameters.
D) We cannot use a regression line to measure the effects of multiple treatments.
A) Connecting the dots generally will not form a line.
B) Using averages for each treatment level will generally create bias.
C) This will cause us to have too few equations to solve for our unknown parameters.
D) We cannot use a regression line to measure the effects of multiple treatments.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
6
If one was estimating a simple regression of Earnings (Y) on Height of individuals (X), and got a coefficient on the Height variable of 30, what would the intercept be if you added 3 inches to every individual in the sample but kept their earnings the same?
A) 30
B) Above 30, but not enough information to tell exactly.
C) Below 30, but not enough information to tell exactly.
D) None of these choices are correct.
A) 30
B) Above 30, but not enough information to tell exactly.
C) Below 30, but not enough information to tell exactly.
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
7
The difference between the observed outcome and the corresponding point on the regression line for a given observation is a:
A) regression line prediction.
B) heteroskedasticity.
C) residual.
D) mean squared error.
A) regression line prediction.
B) heteroskedasticity.
C) residual.
D) mean squared error.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
8
The process of using a function to describe the relationship among variables is known as:
A) regression analysis.
B) big data.
C) business analytics.
D) cross validation.
A) regression analysis.
B) big data.
C) business analytics.
D) cross validation.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
9
A treatment that only undergoes two statuses - treated and untreated-is known as this kind of treatment?
A) Biased
B) Random assignment
C) Dichotomous
D) Attenuated
A) Biased
B) Random assignment
C) Dichotomous
D) Attenuated

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
10
In the dichotomous regression if one was to replace the regression line prediction of the outcome means (for treated/untreated) with medians, which of the following conditions would hold?
A) The sum of all the residuals would equal zero.
B) The sum of the residuals for the treated observations would equal zero.
C) The slope of the regression line would be positive.
D) The number of strictly positive residuals would equal the number of strictly negative residuals.
A) The sum of all the residuals would equal zero.
B) The sum of the residuals for the treated observations would equal zero.
C) The slope of the regression line would be positive.
D) The number of strictly positive residuals would equal the number of strictly negative residuals.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
11
For a dichotomous treatment regression (X = 1 or 0), the mean outcome for the treated group (X = 1) is 35 and the mean outcome for the untreated group is 67. What will the slope of the regression line be?
A) 67
B) 35
C) 67/2 = 33.5
D) -32
A) 67
B) 35
C) 67/2 = 33.5
D) -32

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
12
In a dichotomous regression which condition must hold?
A) For the treated observations, an equal number of positive and negative residuals.
B) For the untreated observations, an equal number of positive and negative residuals.
C) Across all of the observations, an equal number positive and negative residuals.
D) The sum of the residuals for treated and untreated groups must be equal.
A) For the treated observations, an equal number of positive and negative residuals.
B) For the untreated observations, an equal number of positive and negative residuals.
C) Across all of the observations, an equal number positive and negative residuals.
D) The sum of the residuals for treated and untreated groups must be equal.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following treatments is a multi-level treatment?
A) Receiving a cancer drug or a placebo
B) A product is advertised or it isn't
C) Employees receive bonus levels based on years of service
D) None of the answers is correct.
A) Receiving a cancer drug or a placebo
B) A product is advertised or it isn't
C) Employees receive bonus levels based on years of service
D) None of the answers is correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose the regression line to describe the relationship between Y and a dichotomous treatment (X = 1 for treated, = 0 untreated) is given by Y = 4 + 3X. Suppose that one of the observations that was treated was observed to have an outcome, Y = 8. For this observation, what is the residual?
A) 0
B) 7
C) 1
D) -1
A) 0
B) 7
C) 1
D) -1

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
15
In the simple linear regression case, (for Y and X) with a multi-level treatment X, the line to be estimated is given by:
A) Y = b + mX
B) Y = mX
C) Y = mX2
D) None of the answers is correct.
A) Y = b + mX
B) Y = mX
C) Y = mX2
D) None of the answers is correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
16
In relating a variable X to a variable Y with the regression line Y = b + mX, what value would be reported for Y when X = 0?
A) b
B) b + m
C) b ± m
D) m
A) b
B) b + m
C) b ± m
D) m

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
17
Why is Line B a better fit for the data in this graph? 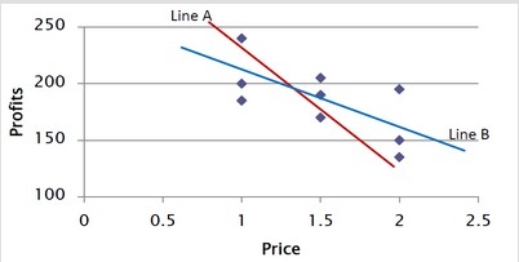
A) For Line B, the average residual (difference between the actual Profits and point on the line) is zero.
B) For Line B, the residuals (difference between the actual Profits and point on the line) are uncorrelated with Price.
C) Line B's slope is less steep than the slope of Line A.
D) Line B's intercept is smaller than Line A's intercept.

A) For Line B, the average residual (difference between the actual Profits and point on the line) is zero.
B) For Line B, the residuals (difference between the actual Profits and point on the line) are uncorrelated with Price.
C) Line B's slope is less steep than the slope of Line A.
D) Line B's intercept is smaller than Line A's intercept.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose your lead analyst runs a simple regression of Profits (Y) on price (X). You know that the average profit in the sample was $1,000 and the average price was $25. If your analyst reports that the intercept from the simple regression is 900, what can you infer about the estimated slope?
A) The estimated slope is 4.
B) The estimated slope is -4.
C) The estimated slope is 2.
D) None of these choices are correct.
A) The estimated slope is 4.
B) The estimated slope is -4.
C) The estimated slope is 2.
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
19
Why is Line A a better fit for the data in this graph? 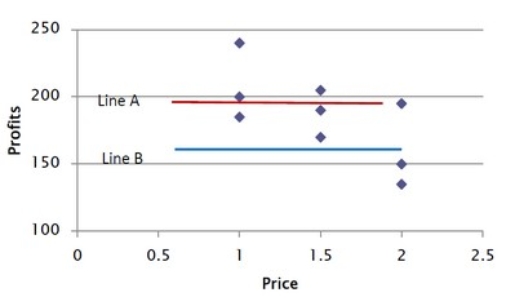
A) For Line B, the average error (difference between the actual Profits and point on the line) is zero.
B) For Line A, the errors (difference between the actual Profits and point on the line) are uncorrelated with Price.
C) For Line A, the average error (difference between the actual Profits and point on the line) is zero.
D) Line B's intercept is smaller than Line A's intercept.

A) For Line B, the average error (difference between the actual Profits and point on the line) is zero.
B) For Line A, the errors (difference between the actual Profits and point on the line) are uncorrelated with Price.
C) For Line A, the average error (difference between the actual Profits and point on the line) is zero.
D) Line B's intercept is smaller than Line A's intercept.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
20
When a treatment can be administered in more than one quantity it is known as a:
A) randomly assigned treatment.
B) dichotomous treatment.
C) multi-level treatment.
D) multiple regression.
A) randomly assigned treatment.
B) dichotomous treatment.
C) multi-level treatment.
D) multiple regression.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
21
In the simple linear regression, the intercept will equal the sample average of the outcome (Y) variable if which of the following is true?
A) sVar(X) > 0
B) = 0
C) sCov(X, Y) > 0
D) sCov(X, Y) < 0
A) sVar(X) > 0
B) = 0
C) sCov(X, Y) > 0
D) sCov(X, Y) < 0

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
22
In the simple linear regression, the intercept will equal the sample average of the outcome (Y) variable if which of the following is true?
A) sCov(X,Y) = 0
B) sVar(X) > 0
C) sCov(X,Y) < 0
D) sVar(Y) > 0
A) sCov(X,Y) = 0
B) sVar(X) > 0
C) sCov(X,Y) < 0
D) sVar(Y) > 0

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
23
In running the simple linear regression of Y on X, if you know that no observation in your sample has an X value that is equal to , what condition might not be true?
A) The regression line's prediction at is .
B) The sum of the residuals equals zero.
C) The average of the residuals equals zero.
D) The residual for the observation closest to will be zero.
A) The regression line's prediction at is .
B) The sum of the residuals equals zero.
C) The average of the residuals equals zero.
D) The residual for the observation closest to will be zero.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
24
In the event that you are trying to explain the variation in Y using the variables X and Z in a linear regression, the multiple regression line would be given by which of the following?
A) Y = b + m1X
B) Y = b + m1Z
C) Y = b + m1X + m2Z
D) Y = b + m1X and Y = b + m1Z
A) Y = b + m1X
B) Y = b + m1Z
C) Y = b + m1X + m2Z
D) Y = b + m1X and Y = b + m1Z

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
25
Which of the following is a reason why estimating the slope and intercept of a simple linear regression line using the least absolute deviations (LAD) approach is not as common as OLS?
A) The objective function for LAD is less intuitive than for OLS.
B) LAD suffers from heteroskedasticity.
C) Taking the absolute value of residuals in most software programs is difficult.
D) The solution for LAD isn't always unique.
A) The objective function for LAD is less intuitive than for OLS.
B) LAD suffers from heteroskedasticity.
C) Taking the absolute value of residuals in most software programs is difficult.
D) The solution for LAD isn't always unique.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
26
Using OLS to solve for the slope and intercept of a simple linear regression will yield a regression line that satisfies which of the following conditions?
A) = 0
B) =
C) Sum of squared residuals equals 0.
D) None of the answers is correct.
A) = 0
B) =
C) Sum of squared residuals equals 0.
D) None of the answers is correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
27
For the simple linear regression, Y = b + mX, which variable is considered the slope coefficient?
A) Y
B) b
C) m
D) X
A) Y
B) b
C) m
D) X

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
28
Why is it helpful to think about the moment conditions of a simple linear regression even if OLS yields the same estimates?
A) The moment conditions are easier to program in Excel.
B) The moment conditions will get the smaller standard errors.
C) The moment conditions establish causality whereas OLS just estimates correlation.
D) The moment conditions facilitate assessing assumptions about causality.
A) The moment conditions are easier to program in Excel.
B) The moment conditions will get the smaller standard errors.
C) The moment conditions establish causality whereas OLS just estimates correlation.
D) The moment conditions facilitate assessing assumptions about causality.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
29
To determine the intercept and slope coefficient in a simple linear regression line of Y on X, all the following conditions will be used except for what?
A) = 0
B) = 0
C) = 0
D) = 0
A) = 0
B) = 0
C) = 0
D) = 0

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
30
All of the following are statements of the criteria used to find the line that "best" describes the data in a multiple regression except for what?
A) The residuals for all data points average to zero.
B) The size of the residuals is not correlated with the treatment level for any treatment.
C) The sum of the residuals for all data points sum to zero.
D) The size of the residuals is not correlated with the outcome level.
A) The residuals for all data points average to zero.
B) The size of the residuals is not correlated with the treatment level for any treatment.
C) The sum of the residuals for all data points sum to zero.
D) The size of the residuals is not correlated with the outcome level.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following sample statistics influences the sign of the slope coefficient in the simple linear regression (of Y on X)?
A) sVar(X)
B) sVar(Y)
C) sCov(X,Y)
D)
A) sVar(X)
B) sVar(Y)
C) sCov(X,Y)
D)

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
32
The methods for solving for the intercept and slope of all of the following procedures will yield identical estimates except for which procedure?
A) Solution to = 0 and = 0
B) Solving minb,m
C) Solution to = 0 and = 0
D) Solving minb,m
A) Solution to = 0 and = 0
B) Solving minb,m
C) Solution to = 0 and = 0
D) Solving minb,m

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
33
Solving for a function that best describes the data that implies the use of OLS (or equivalently, the sample moment equations) potentially in the presence of several treatments is known as:
A) multiple regression.
B) least absolute deviations.
C) instrumental variables regression.
D) two-stage least squares.
A) multiple regression.
B) least absolute deviations.
C) instrumental variables regression.
D) two-stage least squares.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
34
The mean of a function of a random variable(s) for a given sample is known as a(n):
A) sample moment.
B) regression line.
C) heteroskedasticity.
D) unbiased coefficient estimates.
A) sample moment.
B) regression line.
C) heteroskedasticity.
D) unbiased coefficient estimates.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
35
Why is it helpful to think about the moment conditions of a simple linear regression even if OLS yields the same estimates?
A) The moment conditions are easier to program in Excel.
B) The moment conditions will get the smaller standard errors.
C) The moment conditions establish causality whereas OLS just estimates correlation.
D) The moment conditions are used directly to produce the slope and intercept.
A) The moment conditions are easier to program in Excel.
B) The moment conditions will get the smaller standard errors.
C) The moment conditions establish causality whereas OLS just estimates correlation.
D) The moment conditions are used directly to produce the slope and intercept.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
36
The process of solving for the slope and intercept that minimize the sum of squared residuals is a process known as:
A) least absolute deviations.
B) mode estimation.
C) mean squared error.
D) ordinary least squares.
A) least absolute deviations.
B) mode estimation.
C) mean squared error.
D) ordinary least squares.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
37
Using OLS to solve for the slope and intercept of a simple linear regression will yield a regression line that satisfies which of the following conditions?
A) = 0
B) =
C) Sum of squared residuals equals 0
D) None of the answers is correct.
A) = 0
B) =
C) Sum of squared residuals equals 0
D) None of the answers is correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
38
All of the following are conditions that will hold at the estimated coefficients for the simple linear regression line (of Y on X) except for what?
A) Sum of the residuals equals zero.
B) Covariance between the residuals and X is zero.
C) Average of the residuals equals zero.
D) Covariance between Y and the residuals is zero.
A) Sum of the residuals equals zero.
B) Covariance between the residuals and X is zero.
C) Average of the residuals equals zero.
D) Covariance between Y and the residuals is zero.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following settings would require the use of multiple regression (as opposed to simple regression)?
A) Predicting grocery sales as a function of price and local population.
B) Predicting grocery sales as a function of being a weekend day, or a weekday day.
C) Predicting grocery sales as a function of being an AM hour or a PM hour.
D) Predicting grocery sales as a function of local number of competitors.
A) Predicting grocery sales as a function of price and local population.
B) Predicting grocery sales as a function of being a weekend day, or a weekday day.
C) Predicting grocery sales as a function of being an AM hour or a PM hour.
D) Predicting grocery sales as a function of local number of competitors.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
40
An objective function is best described as:
A) the line associating how treatment and outcome variables move together.
B) a function ultimately wished to be maximized or minimized.
C) the function relating the degree of support for a sufficient statistic.
D) the function that determines the degree of freedom.
A) the line associating how treatment and outcome variables move together.
B) a function ultimately wished to be maximized or minimized.
C) the function relating the degree of support for a sufficient statistic.
D) the function that determines the degree of freedom.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
41
If one is planning to use multiple regression to summarize how the variables X1, X2, X3 explain the variation in Y, how many parameters are involved in estimating the linear regression?
A) 2
B) 3
C) 4
D) 5
A) 2
B) 3
C) 4
D) 5

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
42
A critical aspect of linear regression is that:
A) the regression line is linear in parameters.
B) the regression line only involves parameters that are positive.
C) None of the observed variables in the regression have been transformed using the logarithm function.
D) None of the answers is correct.
A) the regression line is linear in parameters.
B) the regression line only involves parameters that are positive.
C) None of the observed variables in the regression have been transformed using the logarithm function.
D) None of the answers is correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
43
If you're running a multiple regression of employee Hours Worked on Tenure (in number of years) and MBA (a binary variable equal to 1 for an employee with an MBA, 0 otherwise), what moment conditions would not be used?
A)
= 0
B)
= 0
C)
= 0
D) = 0
A)
= 0
B)
= 0
C)
= 0
D) = 0

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
44
Which of the following equations cannot be estimated using linear regression techniques?
A) Y = b + m[log(X)]
B) Log(Y) = b + m[log(X)]
C) Y = m1X × m2Z
D) Y = b + mX 2
A) Y = b + m[log(X)]
B) Log(Y) = b + m[log(X)]
C) Y = m1X × m2Z
D) Y = b + mX 2

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
45
If you're running a multiple regression of employee Hours Worked on Tenure (in number of years) and MBA (a binary variable equal to 1 for an employee with an MBA, 0 otherwise), which moment conditions would be used?
A)
= 0
B) = 0
C)
= 0
D) The first two answer options are correct.
A)
= 0
B) = 0
C)
= 0
D) The first two answer options are correct.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
46
If one was attempting to estimate the parameter, b, that best explains the relationship between Sales and price using the following equation Sales = (Price - b)2. Which of the following methods would be the most appropriate to estimate b?
A) Simple linear regression
B) Multiple linear regression
C) Nonlinear regression
D) Probit
A) Simple linear regression
B) Multiple linear regression
C) Nonlinear regression
D) Probit

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
47
If one is trying to explain the time series variation in a stock price for a company by using the number of Twitter mentions that day, which method is most appropriate?
A) Dichotomous treatment regression
B) Simple regression
C) Two stage least squares
D) Probit
A) Dichotomous treatment regression
B) Simple regression
C) Two stage least squares
D) Probit

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
48
If one is planning to use multiple regression to summarize how the variables X1, X2, X3 explain the variation in Y, how many moment conditions are involved in estimating the linear regression?
A) 2
B) 3
C) 4
D) 5
A) 2
B) 3
C) 4
D) 5

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
49
If one is trying to explain the cross-sectional variation in prices for milk across grocery stores in the country using commercial rental prices and a binary variable for if the grocery store chain owns a dairy farm, which method is most appropriate?
A) Multiple regression
B) Simple regression
C) Two stage least squares
D) Probit
A) Multiple regression
B) Simple regression
C) Two stage least squares
D) Probit

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose you're running a multiple regression of Home Prices (in thousands of $) on five different treatment variables including number of bedrooms, number of bathrooms, total square feet, total lot size, and garage size, where all the treatment variables have been standardized . If the coefficient on number of bedrooms is estimated to be 3, how would you interpret the coefficient on the number of bedrooms?
A) Increasing the number of bedrooms by 1, holding number of bathrooms, total square feet, lot and garage size fixed increases the average home price by three thousand dollars.
B) Increasing the number of bedrooms by 3, holding number of bathrooms, total square feet, lot and garage size fixed increases the average home price by a thousand dollars.
C) Increasing the number of bedrooms by 1, increases the average home price by three thousand dollars.
D) Increasing the number of bedrooms by 1 standard deviation, holding number of bathrooms, total square feet, lot and garage size fixed increases the average home price by three thousand dollars.
A) Increasing the number of bedrooms by 1, holding number of bathrooms, total square feet, lot and garage size fixed increases the average home price by three thousand dollars.
B) Increasing the number of bedrooms by 3, holding number of bathrooms, total square feet, lot and garage size fixed increases the average home price by a thousand dollars.
C) Increasing the number of bedrooms by 1, increases the average home price by three thousand dollars.
D) Increasing the number of bedrooms by 1 standard deviation, holding number of bathrooms, total square feet, lot and garage size fixed increases the average home price by three thousand dollars.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose you're running a multiple regression of Home Prices on two treatment variables, City, which is a binary variable for whether or not the home is located in a city or not, and Finished Basement, which is a binary variable for whether or not the home has a finished basement. If you solve for the multiple regression using the moment conditions all of the following conditions must hold except for what?
A) The sum of residuals must equal zero.
B) The correlation between the residuals and Home Prices must be equal to zero.
C) The correlation between the residuals and City must be equal to zero.
D) The correlation between the residuals and Finished Basement must be equal to zero.
A) The sum of residuals must equal zero.
B) The correlation between the residuals and Home Prices must be equal to zero.
C) The correlation between the residuals and City must be equal to zero.
D) The correlation between the residuals and Finished Basement must be equal to zero.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose you're running a multiple regression of Home Prices on two treatment variables, City, which is a binary variable for whether or not the home is located in a city or not, and Finished Basement, which is a binary variable for whether or not the home has a finished basement. If you solve for the multiple regression using the moment conditions which condition must hold?
A) The sum of squared residuals must equal zero.
B) The sum of absolute residuals must equal zero.
C) The sum of the residuals for the observations with Finished Basements (=1) must be zero.
D) The correlation between the residuals and Home Prices must be equal to zero.
A) The sum of squared residuals must equal zero.
B) The sum of absolute residuals must equal zero.
C) The sum of the residuals for the observations with Finished Basements (=1) must be zero.
D) The correlation between the residuals and Home Prices must be equal to zero.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose you're running a multiple regression of Home Prices on five different treatment variables including number of bedrooms, number of bathrooms, total square feet, total lot size, and garage size, where all the treatment variables have been standardized . Which conditions about the multiple regression must hold?
A) Correlation between each of the treatment variables equals 0.
B) Correlation between each of the treatment variables equals 1.
C) Intercept for the multiple linear regression equals the sample average home price.
D) Correlation between the residuals and home price equals 0.
A) Correlation between each of the treatment variables equals 0.
B) Correlation between each of the treatment variables equals 1.
C) Intercept for the multiple linear regression equals the sample average home price.
D) Correlation between the residuals and home price equals 0.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck


