Deck 10: Derivatives: Risk Management With Speculation, Hedging, and Risk Transfer
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 10: Derivatives: Risk Management With Speculation, Hedging, and Risk Transfer
1
Why are futures contracts commonly believed to be less subject to default risk than forward contracts?
Futures markets have put in place successful procedures to protect clients from the default of
a counterparty:
The counterparty is always the clearinghouse, not a private party.
A centralized margin deposit system.
Guarantees posted by all members who are collectively responsible.
Daily marking-to-market. Variation limits can make this process take place during the day if needed.
Liquidity of an organized market for standardized contracts.
a counterparty:
The counterparty is always the clearinghouse, not a private party.
A centralized margin deposit system.
Guarantees posted by all members who are collectively responsible.
Daily marking-to-market. Variation limits can make this process take place during the day if needed.
Liquidity of an organized market for standardized contracts.
2
You wish to establish the theoretical futures price on a Euribor contract quoted on the London International Financial Futures Exchange (LIFFE) in London. The futures contract is for a 90-day Euribor rate at expiration of the futures contract. You look at the current term structure of Euribor interest rates. Following the standard conventions for short-term rates, all interest rates are quoted as annualized linear rates. In other words, the interest paid for a maturity of T days is equal to the annualized rate quoted, divided by 360 and multiplied by T. The observed rates are as follows:
a. What should be the Euribor futures price quoted today with an expiration date in exactly
90 days?
b. What should be the Euribor futures price quoted today with an expiration date in exactly
60 days?
a. What should be the Euribor futures price quoted today with an expiration date in exactly
90 days?
b. What should be the Euribor futures price quoted today with an expiration date in exactly
60 days?
a. This futures contract is for a 90-day bill issued in 90 days and maturing in 180 days. The annualized forward interest rate rF is given by: rF =4.80%
F=100% - 4.80% = 95.20%.
b. This futures contract is for a 90-day bill issued in 60 days and maturing in 150 days. The annualized forward interest rate rF is given by: rF = 4.72%
F = 100% - 4.72% = 95.28%.
F=100% - 4.80% = 95.20%.
b. This futures contract is for a 90-day bill issued in 60 days and maturing in 150 days. The annualized forward interest rate rF is given by: rF = 4.72%
F = 100% - 4.72% = 95.28%.
3
To capitalize on your expectation of a 10% gold price appreciation, you consider buying futures or option contracts to speculate. The spot price of gold is $400. Near-delivery futures contracts are quoted at $410 per ounce with a margin of $1,000 per contract of 100 ounces. Call options on gold are quoted with the same delivery date. A call with an exercise price of $400 costs $20 per ounce. The rate of return on your speculation will be the return on your invested capital, which is the initial margin for futures and the option premium for options.
a. Based on your expectation of a 10% rise in gold price, what is your expected return at maturity on futures contracts?
b. Based on your expectation of a 10% rise in gold price, what is your expected return at maturity on option contracts?
c. Simulate the return of the two investments for various movements in the price of gold.
a. Based on your expectation of a 10% rise in gold price, what is your expected return at maturity on futures contracts?
b. Based on your expectation of a 10% rise in gold price, what is your expected return at maturity on option contracts?
c. Simulate the return of the two investments for various movements in the price of gold.
a The expected rate of return on the futures margin deposit is equal to 300%. This is found by observing that the margin per ounce of gold is $10($1,000 for contract of 100 ounces). With a 10% gold price appreciation of $40, the spot price of gold will rise to $440, which will also be the futures price on delivery date. Hence, a profit of $440 - $410 = $30, for an initial investment of $10.
b. At expiration, the option is expected to be worth $40 per ounce, since the gold price is expected to be $440 and the exercise price is $400 per ounce. This leads to a net profit of $20 and a rate of return on the initial $20 investment of 100%.
c. Gold Price Simulation
b. At expiration, the option is expected to be worth $40 per ounce, since the gold price is expected to be $440 and the exercise price is $400 per ounce. This leads to a net profit of $20 and a rate of return on the initial $20 investment of 100%.
c. Gold Price Simulation
4
A German investor holds a portfolio of British stocks. The market value of the portfolio is £20 million, with a of 1.5 relative to the FTSE index. In November, the spot value of the FTSE index is 4,000. The dividend yield, euro interest rates, and pound interest rates are all equal to 4% (flat yield curves).
a. The German investor fears a drop in the British stock market (but not in the British pound).
The size of FTSE stock index contracts is 10 pounds times the FTSE index. There are futures contracts quoted with December delivery. Calculate the futures price of the index.
b. How many contracts should you buy or sell to hedge the British stock market risk?
c. You believe that the capital asset pricing model (CAPM) applies to British stocks. The expected stock market return is 10%. What is the expected return on this portfolio before and after hedging?
d. You now fear a depreciation of the British pound relative to the euro. Will the strategies above protect you against this depreciation? (Assume that the margin on the futures contract is deposited in euros.)
e. The forward exchange rate is equal to 1.4 € per £. How many pounds should you sell forward?
a. The German investor fears a drop in the British stock market (but not in the British pound).
The size of FTSE stock index contracts is 10 pounds times the FTSE index. There are futures contracts quoted with December delivery. Calculate the futures price of the index.
b. How many contracts should you buy or sell to hedge the British stock market risk?
c. You believe that the capital asset pricing model (CAPM) applies to British stocks. The expected stock market return is 10%. What is the expected return on this portfolio before and after hedging?
d. You now fear a depreciation of the British pound relative to the euro. Will the strategies above protect you against this depreciation? (Assume that the margin on the futures contract is deposited in euros.)
e. The forward exchange rate is equal to 1.4 € per £. How many pounds should you sell forward?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
Derive a theoretical price for each of the following futures contracts quoted in the United States and indicate why and how the market price should deviate from this theoretical value. In each case, consider one unit of underlying asset. The contract expires in exactly three months, and the annualized interest rate on three-month dollar London InterBank Offered Rate (LIBOR) is 12%.
All interest rates quoted are annualized.
All interest rates quoted are annualized.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
A few years ago when the French franc (FF) still existed, the MATIF futures exchange in Paris had a very active market for the French government bond contract. The underlying asset is a notional long-term government bond with a yield of 10%. The size of the contract is FF 500,000 of nominal value. Futures prices are quoted in percentage of the nominal value. On April 1, the French term structure of interest rate is flat. The bond futures price for delivery in June is equal to 106.21%. The three French government bonds that can be used for delivery have the following characteristics:
a. Is the futures price consistent with the spot bond prices? (Find the bond cheapest to deliver.)
b. Estimate the interest rate sensitivity (duration) of the futures price.
c. You are an insurance company with a portfolio of French government bonds. The portfolio has a nominal value of FF 100 million and a market value of FF 110 million. Its average duration is 3.5. You are worried that social unrest in France could lead to an increase in French interest rates. Rather than selling the bonds, you wish to temporarily hedge the French interest rate risk. How many futures contracts would you sell and why?
Note to the instructor: The section on optimal hedge ratios for bond portfolios has been removed from the 5th edition. We include a brief summary of the theoretical derivations
given at the end of the solution.
a. Is the futures price consistent with the spot bond prices? (Find the bond cheapest to deliver.)
b. Estimate the interest rate sensitivity (duration) of the futures price.
c. You are an insurance company with a portfolio of French government bonds. The portfolio has a nominal value of FF 100 million and a market value of FF 110 million. Its average duration is 3.5. You are worried that social unrest in France could lead to an increase in French interest rates. Rather than selling the bonds, you wish to temporarily hedge the French interest rate risk. How many futures contracts would you sell and why?
Note to the instructor: The section on optimal hedge ratios for bond portfolios has been removed from the 5th edition. We include a brief summary of the theoretical derivations
given at the end of the solution.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
An Italian corporation enters into a two-year interest rate swap in euros on April 1, 2000. The swap is based on a principal of €100 million, and the corporation will receive 7% fixed and pay six-month Euribor. Swap payments are semiannual. The 7% fixed rate is quoted as an annual rate using the European method, so the implied semiannual coupon is 3.44% [since (1.0344)2 = 1.07]. Two years later, the swap is finally settled, and the following Euribor rates have been observed:
a. What have the swap payments or receipts for the corporation been on each swap payment date?
b. The same Italian corporation also entered another two-year interest rate swap in euros on April 1, 2000. The swap is based on a principal of €100 million, and the corporation contracted to receive 7% fixed and pay six-month Euribor. On this swap, the payments are annual. Hence, the two successive six-month Euribor are compounded. Assuming that the Euribor rates given in the previous problem have been observed, what have the two annual swap payments been?
a. What have the swap payments or receipts for the corporation been on each swap payment date?
b. The same Italian corporation also entered another two-year interest rate swap in euros on April 1, 2000. The swap is based on a principal of €100 million, and the corporation contracted to receive 7% fixed and pay six-month Euribor. On this swap, the payments are annual. Hence, the two successive six-month Euribor are compounded. Assuming that the Euribor rates given in the previous problem have been observed, what have the two annual swap payments been?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
A swap dealer provides the following quotations for a yen/$ currency swap. The quotes are for a yen fixed rate against the U.S. Treasury yield flat, with annual payments.
 A client wishes to enter a five-year swap, paying yen and receiving $. The current yield on five-year U.S. Treasury bonds is 7.20%, using the semiannual method, which amounts to 7.33%, using the annual European method.
A client wishes to enter a five-year swap, paying yen and receiving $. The current yield on five-year U.S. Treasury bonds is 7.20%, using the semiannual method, which amounts to 7.33%, using the annual European method.
What will the exact terms of the swap be if the client accepts these quotations?
 A client wishes to enter a five-year swap, paying yen and receiving $. The current yield on five-year U.S. Treasury bonds is 7.20%, using the semiannual method, which amounts to 7.33%, using the annual European method.
A client wishes to enter a five-year swap, paying yen and receiving $. The current yield on five-year U.S. Treasury bonds is 7.20%, using the semiannual method, which amounts to 7.33%, using the annual European method.What will the exact terms of the swap be if the client accepts these quotations?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
You specialize in arbitrage between the futures and the cash market on the Paris Bourse. The CAC stock index is made up of 40 leading stocks. The futures price of the CAC contract with delivery in a month is 2,120. The size of the contract is €10 times the index. The spot value of the index is given as 2,000. Actually, there are transaction costs in the cash market; the bid-ask spread is around 40 points. You can buy a basket of stocks representing the index for 2,020 and sell the same basket for 1,980. Transaction costs on the futures contracts are assumed to be negligible. During the next month, the stocks in the index will pay dividends amounting to 5 per index. These dividends have already been announced, so there is no uncertainty about this cash flow. The current one-month interest rate in euros is 61/2 -5/8%.
a. Do you detect any arbitrage opportunity?
b. What profit could you make per contract?
c. What is the theoretical value of the futures bid and ask prices?
a. Do you detect any arbitrage opportunity?
b. What profit could you make per contract?
c. What is the theoretical value of the futures bid and ask prices?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
In Hong Kong, the size of a futures contract on the Hang Seng stock index is HK $50 times the index. The margin (initial and maintenance) is set at HK $32,500. You predict a drop in the Hong Kong stock market following some economic problems in China and decide to sell one June futures contract on April 1. The current futures price is 7,200. The contract expires on the second-to-last business day of the delivery month (expiration date: June 27). Today is April 1, and the current spot value of the stock market index is 7,140.
a. Why is the spot value of the index lower than the futures value of the index?
b. Indicate the cash flows that affect your position if the following prices are subsequently observed:

a. Why is the spot value of the index lower than the futures value of the index?
b. Indicate the cash flows that affect your position if the following prices are subsequently observed:


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
A money manager holds $50 million worth of top-quality international bonds denominated in dollars. Their face value is $40 million, and most issues are highly illiquid. She fears a rise in U.S. interest rates and decides to hedge, using U.S. Treasury bond futures. Why would it be difficult to achieve a perfect hedge (list the various reasons)?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
Let's consider a Swiss franc futures contract traded in the United States. On February 18 (a Friday), the March contract closed at 0.7049 dollar per Swiss franc. The size of the contract is 125,000 Swiss francs. The initial margin is $2,600 per contract and the maintenance margin is $1,600. Assume that you buy one March contract on February 19 at 0.7049 $/SFr and you deposit, in cash, an initial margin of $2,600. Listed below are the futures quotations (settlement prices) observed on three successive days:
What are the cash flows associated with the marking-to-market procedure?
What are the cash flows associated with the marking-to-market procedure?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
Pouf is a rapidly growing and pleasant country in the Austral hemisphere. Its inhabitants are called Poufans, and its currency is the pof. The bond market is fairly active with many issues by Poufan companies, but there are no foreign investors or issuers. The current yield on pof bonds is 10%. Poufan investors have to pay a 15% tax on interest income received. The newly elected Poufan government wishes to internationalize its bond market and attract foreign issuers. To do so, it decides to remove any taxation of income on bonds issued by foreign corporations in Pouf. Several changes take place after the enactment of this tax provision:
Several well-known foreign corporations issue pof-denominated bonds in the Poufan bond market.
Several well-known Poufan corporations issue international bonds denominated in U.S. dollars.
Several dollar/pof swaps are arranged.
Try to provide a sensible explanation for this phenomenon.
Several well-known foreign corporations issue pof-denominated bonds in the Poufan bond market.
Several well-known Poufan corporations issue international bonds denominated in U.S. dollars.
Several dollar/pof swaps are arranged.
Try to provide a sensible explanation for this phenomenon.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
A manager holds a diversified portfolio of British stocks worth £5 million. He has short-term fears about the market but feels that it is a sound long-term investment. He is a firm believer in betas, and his portfolio's is equal to 0.8. What are the alternatives open to temporarily reduce the risk on his British portfolio?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
A Swiss portfolio manager has a significant portion of the portfolio invested in dollar-denominated assets. The money manager is worried about the political situation surrounding the next U.S. presidential election and fears a potential drop in the value of the dollar. The manager decides to
sell the dollars forward against Swiss francs.
a. Give some reasons why the Swiss money manager should use futures rather than forward currency contracts?
b. Give some reasons why the Swiss money manager should use forward currency contracts rather than futures?
sell the dollars forward against Swiss francs.
a. Give some reasons why the Swiss money manager should use futures rather than forward currency contracts?
b. Give some reasons why the Swiss money manager should use forward currency contracts rather than futures?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
A dollar-Swiss franc swap with a maturity of five years was contracted by Papaf Inc. three years ago. Papaf swapped $100 million for CHF 250 million. The swap payments were annual, based on market interest rates of 8% in dollars and 4% in CHF. In other words, Papaf Inc. contracted to pay dollars and receive CHF. The current spot exchange rate is 2 CHF/$, and the current interest rates are 6% in CHF and 10% in $ (the term structures are flat).
a. What is the swap payment at the end of year three? Does Papaf pay or receive?
b. On the final date of the swap, the spot exchange rate is 1.5 CHF/$.
What is the final swap payment at the end of year five?
a. What is the swap payment at the end of year three? Does Papaf pay or receive?
b. On the final date of the swap, the spot exchange rate is 1.5 CHF/$.
What is the final swap payment at the end of year five?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
A Dutch institutional investor has decided to bet on a drop in U.S. dollar bond yields. It engages in a leveraged strategy, borrowing $100 million at LIBOR plus 0.25% and investing the proceeds in attractive, newly issued, long-term dollar international bonds. Suddenly, the investor becomes worried that bond yields have hit bottom and will rise because of inflationary pressures. The investor wishes to keep the specific international bonds that have been selected, partly because of their attractiveness and partly because of their lack of market liquidity. What kind of swap could be arranged to hedge this U.S. dollar bond yield risk?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
You are the treasurer of a major Japanese construction company. Today is January 15. You expect to receive €10 million at the end of March, as payment from a client on some construction work in France. You know that you will need this sum somewhere else in Europe at the end of June. Meanwhile, you wish to invest these €10 million for three months. The current three-month interest rate in euros is 4%, but you are worried that it will quickly drop. Listed below are Euribor futures quotations on EUREX:
a. Knowing that Euribor contracts have a size of €1 million, what should you do to freeze a lending rate when you will receive the money?
b. At the end of March, when you receive the money, the three-month Euribor is equal to 3%.
How much money (number of euros) have you gained by engaging in the above transaction
(as opposed to doing nothing on January 15)?
a. Knowing that Euribor contracts have a size of €1 million, what should you do to freeze a lending rate when you will receive the money?
b. At the end of March, when you receive the money, the three-month Euribor is equal to 3%.
How much money (number of euros) have you gained by engaging in the above transaction
(as opposed to doing nothing on January 15)?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
An American investor wants to invest in a diversified portfolio of Japanese stocks but can invest only a rather small sum. The investor also worries about fiscal and transaction cost considerations. Why would futures contracts on the Nikkei index be an attractive alternative?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
You hold a portfolio made of French stocks and worth €10 million. The beta ( ) of this portfolio relative to the CAC index is 1.5. The interest rate for the euro is 4% for all maturities and the annual dividend yield is 2%. The spot value of the CAC index on January 1, 2000, is 5,000. A CAC contract has a size of €10 for each index point.
a. What should be the future price of the CAC contract with a three-month maturity?
b. You fear a fall in the French stock market. What should be your hedge ratio? How many contracts do you buy/sell?
a. What should be the future price of the CAC contract with a three-month maturity?
b. You fear a fall in the French stock market. What should be your hedge ratio? How many contracts do you buy/sell?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
If the average premium on gold call options declines, does this mean that they are becoming undervalued and, therefore, should be bought? Using valuation models, give at least two possible reasons for this decline.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
The average premium on currency calls has decreased, whereas the premium on currency puts has increased. What explanations can you provide?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
You will receive $10 million at the end of June and will invest it for three months on the Eurodollar market. The current three-month Eurodollar rate is 6%, and you are worried that the rate will drop by the end of June. Here are some market quotes:
Eurodollar LIBOR futures, June delivery: Price 94%.
Call eurodollar, June expiration, strike price 94%: Premium 0.4%.
Put Eurodollar, June expiration, strike price 94%: Premium 0.4%.
The contract sizes are $1 million.
a. Should you buy or sell futures to hedge your interest rate risk?
b. Should you buy (or sell) calls (or puts) to insure a minimum rate at the time you will invest your money? What is this rate?
c. In June, the Eurodollar rate has moved to 4%. What is the result of your strategies using futures and using options?
d. What if the rate is equal to 8% in June?
Eurodollar LIBOR futures, June delivery: Price 94%.
Call eurodollar, June expiration, strike price 94%: Premium 0.4%.
Put Eurodollar, June expiration, strike price 94%: Premium 0.4%.
The contract sizes are $1 million.
a. Should you buy or sell futures to hedge your interest rate risk?
b. Should you buy (or sell) calls (or puts) to insure a minimum rate at the time you will invest your money? What is this rate?
c. In June, the Eurodollar rate has moved to 4%. What is the result of your strategies using futures and using options?
d. What if the rate is equal to 8% in June?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
The current yield curve on the international bond market in euro is flat at 4% for top-quality borrowers. A French company of good standing can issue plain-vanilla straight and floating-rate bonds at the following conditions:
Bond A: Straight Bond. Five-year straight bond with a fixed coupon of 4%.
Bond B: FRN. Five-year dollar FRN with a semiannual coupon set at LIBOR.
An investment banker proposes to the French company to issue bull and/or bear FRNs at the following conditions:
Bond C: Bull FRN. Five-year FRN with a semiannual coupon set at:
7.60% - LIBOR.
Bond D: Bear FRN. Five-year FRN with a semiannual coupon set at:
2*LIBOR - 4.2%.
The floor on all coupons is zero. The investment bank also proposes a five-year floor option at a strike of 2.1%. This floor will pay to the French company the difference between 2.1% and LIBOR, if it is positive, or zero if LIBOR is above 2.1%. The cost of this floor is spread over the payment dates and set at an annual 0.05%. The bank also proposes a five-year cap at a strike of 7.60%. The annual premium on the cap is 0.1%. The company can also enter in a five-year interest-rate swap 4% fixed against LIBOR.
a. Assume that the French company issues Bonds C and D in equal proportions. Is it more advantageous than issuing Bonds A and B in equal proportion and why?
b. Find out the borrowing cost reduction that can be achieved by issuing the bull note compared to issuing a fixed-coupon straight bond at 4%.
c. Find out the borrowing cost reduction that can be achieved by issuing the bull note compared to issuing a plain-vanilla FRN at LIBOR.
d. Find out the borrowing cost reduction that can be achieved by issuing the bear note compared to issuing a fixed-coupon straight bond at 4%.
e. Find out the borrowing cost reduction that can be achieved by issuing the bear note compared to issuing a plain-vanilla FRN at LIBOR.
Bond A: Straight Bond. Five-year straight bond with a fixed coupon of 4%.
Bond B: FRN. Five-year dollar FRN with a semiannual coupon set at LIBOR.
An investment banker proposes to the French company to issue bull and/or bear FRNs at the following conditions:
Bond C: Bull FRN. Five-year FRN with a semiannual coupon set at:
7.60% - LIBOR.
Bond D: Bear FRN. Five-year FRN with a semiannual coupon set at:
2*LIBOR - 4.2%.
The floor on all coupons is zero. The investment bank also proposes a five-year floor option at a strike of 2.1%. This floor will pay to the French company the difference between 2.1% and LIBOR, if it is positive, or zero if LIBOR is above 2.1%. The cost of this floor is spread over the payment dates and set at an annual 0.05%. The bank also proposes a five-year cap at a strike of 7.60%. The annual premium on the cap is 0.1%. The company can also enter in a five-year interest-rate swap 4% fixed against LIBOR.
a. Assume that the French company issues Bonds C and D in equal proportions. Is it more advantageous than issuing Bonds A and B in equal proportion and why?
b. Find out the borrowing cost reduction that can be achieved by issuing the bull note compared to issuing a fixed-coupon straight bond at 4%.
c. Find out the borrowing cost reduction that can be achieved by issuing the bull note compared to issuing a plain-vanilla FRN at LIBOR.
d. Find out the borrowing cost reduction that can be achieved by issuing the bear note compared to issuing a fixed-coupon straight bond at 4%.
e. Find out the borrowing cost reduction that can be achieved by issuing the bear note compared to issuing a plain-vanilla FRN at LIBOR.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
A small German bank has the following portfolio of loans in U.S. dollars, valued at market value:
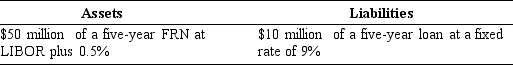 The German bank fears a long-term depreciation of the U.S. dollar relative to the euro and believes in stable U.S. interest rates.
The German bank fears a long-term depreciation of the U.S. dollar relative to the euro and believes in stable U.S. interest rates.
a. What is its currency exposure?
b. What type of swap arrangements should it contract?
c. What should the principal of the swaps be?
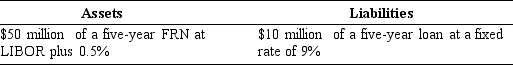 The German bank fears a long-term depreciation of the U.S. dollar relative to the euro and believes in stable U.S. interest rates.
The German bank fears a long-term depreciation of the U.S. dollar relative to the euro and believes in stable U.S. interest rates.a. What is its currency exposure?
b. What type of swap arrangements should it contract?
c. What should the principal of the swaps be?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
Assume that an AAA customer pays 8% on a five-year loan and can contract a five-year interest
rate swap (paying fixed) at 8% against LIBOR. Assume that a BBB customer pays (8 +0 m)% on a
five-year loan and can contract a five-year interest rate swap (paying fixed) at (8 + µ)% against LIBOR. Should a customer pay the same credit-quality spread (m and µ) on a loan and on a swap?
rate swap (paying fixed) at 8% against LIBOR. Assume that a BBB customer pays (8 +0 m)% on a
five-year loan and can contract a five-year interest rate swap (paying fixed) at (8 + µ)% against LIBOR. Should a customer pay the same credit-quality spread (m and µ) on a loan and on a swap?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
The French futures market, MATIF, trades Euribor contracts. The Euribor is the three-month interbank interest rate on euros. The contract size is €1 million, and the margin is €3,000. On
January 10, March futures trade at 90.74%. Options on the Euribor futures contract are also listed. The premiums (in %) on March options are as follows:
A few days later (January 14), the futures price moves to 89.50.
a. What is the gain or loss, in euros, for someone who sold a futures contract on January 10?
b. What is the return, as a percentage of the initial investment (margin)?
c. Are all option premiums quoted on January 10 reasonable?
d. You know that you will have to borrow €10 million in March and fear a rise in interest rates. What are the maximum borrowing rates that you can insure using the various options?
e. To cap your borrowing rate, you decide to use options with a strike price of 90.80. How many calls (or puts) should you buy (or sell)?
On January 14, the premium on the call March 90.80 moves to 0.02, and the premium on the put March 90.80 moves to 1.33.
f. What is the € profit (or loss) on your option position?
g. What is the rate of return on your option position?
January 10, March futures trade at 90.74%. Options on the Euribor futures contract are also listed. The premiums (in %) on March options are as follows:
A few days later (January 14), the futures price moves to 89.50.
a. What is the gain or loss, in euros, for someone who sold a futures contract on January 10?
b. What is the return, as a percentage of the initial investment (margin)?
c. Are all option premiums quoted on January 10 reasonable?
d. You know that you will have to borrow €10 million in March and fear a rise in interest rates. What are the maximum borrowing rates that you can insure using the various options?
e. To cap your borrowing rate, you decide to use options with a strike price of 90.80. How many calls (or puts) should you buy (or sell)?
On January 14, the premium on the call March 90.80 moves to 0.02, and the premium on the put March 90.80 moves to 1.33.
f. What is the € profit (or loss) on your option position?
g. What is the rate of return on your option position?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
Four years ago, a Swiss firm contracted a currency swap of US$100 million for 250 million Swiss francs (SFr), with a maturity of seven years. The swap fixed rates are 8% in dollars and 4% in francs, and swap payments are annual. The Swiss firm contracted to pay dollars and receive francs. The market conditions are now (exactly four years later) as follows:
Spot exchange rate: 2.00 Swiss francs/U.S. dollar.
Term structure of zero swap rates:
a. What should the swap payment (receipt) be at the end of the fourth year, that is, today?
b. Right after this payment, what is the swap market value for the Swiss firm?
Spot exchange rate: 2.00 Swiss francs/U.S. dollar.
Term structure of zero swap rates:
a. What should the swap payment (receipt) be at the end of the fourth year, that is, today?
b. Right after this payment, what is the swap market value for the Swiss firm?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
A small French bank has the following balance sheet, based on historical (nominal) values.
All assets and liabilities are denominated in euros. The net worth is calculated as the difference between the value of assets and liabilities. The current interest rate term structure in euro is flat at 8%. The risk premium over Euribor required on the loan to a client remains at 50 basis points.
a. Value the balance sheet based on market value.
b. The bank anticipates a sharp drop in French interest rates. Would this drop be good for the bank?
The current market conditions for interest rate swaps with a maturity of three or five years are 8% against Euribor.
c. Assume that the bank simply wishes to immunize its market value against any movements in interest rates (drop or rise). What swap would you make to hedge this interest rate risk?
d. Assume that the bank is quite confident in its interest rate prediction (a drop). What would you suggest?
The next day, all interest rates drop to 7%.
e. Value the balance sheet again, assuming that the floating rate debt remains at 100% and that the bank has undertaken the swap that you recommended. How much did the bank save by undertaking this swap?
All assets and liabilities are denominated in euros. The net worth is calculated as the difference between the value of assets and liabilities. The current interest rate term structure in euro is flat at 8%. The risk premium over Euribor required on the loan to a client remains at 50 basis points.
a. Value the balance sheet based on market value.
b. The bank anticipates a sharp drop in French interest rates. Would this drop be good for the bank?
The current market conditions for interest rate swaps with a maturity of three or five years are 8% against Euribor.
c. Assume that the bank simply wishes to immunize its market value against any movements in interest rates (drop or rise). What swap would you make to hedge this interest rate risk?
d. Assume that the bank is quite confident in its interest rate prediction (a drop). What would you suggest?
The next day, all interest rates drop to 7%.
e. Value the balance sheet again, assuming that the floating rate debt remains at 100% and that the bank has undertaken the swap that you recommended. How much did the bank save by undertaking this swap?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
You are an investment banker working in Switzerland where yields are very low (1% for all maturities). You are planning to offer a five-year Swiss franc/British pound bond with the following characteristics:
Issuer: Brit Ltd., a top-quality British company.
Issue amount: SFr 100 million.
Coupon in SFr: 5% (or SFr 5 million).
Reimbursed value: £40 million.
This bond qualifies as a Swiss franc bond for the portfolio of a Swiss insurance company.
The current spot exchange rate is 2.5 Swiss francs per British pound. The yield curve in British pounds is flat at 7%. The pound/franc swap rates are 7% in pounds against 1% in francs for all maturities.
a. Assume that Swiss insurance companies can account for their Swiss franc bond holdings
at historical costs. Give a reason why it would be attractive to invest in this bond.
b. Is the coupon rate set at fair pricing (i.e., consistent with current market conditions)?
c. The British company desires to borrow in pounds and does not wish to carry any currency risk on its debt. The investment banker needs to design a coupon swap that would hedge the currency risk on that dual-currency bond for Brit Ltd. The designed swap should have a zero value at time of contracting. Give one possible design for the swap and calculate its associated swap rate.
d. What is the pound yield paid by the British company, once it has hedged its currency risk on the dual-currency bond using the swap described above? What is the annual cost-saving in British pounds compared to a straight pound bond?
Issuer: Brit Ltd., a top-quality British company.
Issue amount: SFr 100 million.
Coupon in SFr: 5% (or SFr 5 million).
Reimbursed value: £40 million.
This bond qualifies as a Swiss franc bond for the portfolio of a Swiss insurance company.
The current spot exchange rate is 2.5 Swiss francs per British pound. The yield curve in British pounds is flat at 7%. The pound/franc swap rates are 7% in pounds against 1% in francs for all maturities.
a. Assume that Swiss insurance companies can account for their Swiss franc bond holdings
at historical costs. Give a reason why it would be attractive to invest in this bond.
b. Is the coupon rate set at fair pricing (i.e., consistent with current market conditions)?
c. The British company desires to borrow in pounds and does not wish to carry any currency risk on its debt. The investment banker needs to design a coupon swap that would hedge the currency risk on that dual-currency bond for Brit Ltd. The designed swap should have a zero value at time of contracting. Give one possible design for the swap and calculate its associated swap rate.
d. What is the pound yield paid by the British company, once it has hedged its currency risk on the dual-currency bond using the swap described above? What is the annual cost-saving in British pounds compared to a straight pound bond?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
You are currently borrowing €10 million at three-month Euribor + 75 basis points. The Euribor is
at 3%. You expect to borrow this amount for five years but are worried that Euribor will rise in the future. You can buy a 4% cap on three-month Euribor over the next five years with an annual cost of 0.75% (paid quarterly). Describe the evolution of your borrowing costs under various interest rate scenarios (i.e., above and below 4%).
at 3%. You expect to borrow this amount for five years but are worried that Euribor will rise in the future. You can buy a 4% cap on three-month Euribor over the next five years with an annual cost of 0.75% (paid quarterly). Describe the evolution of your borrowing costs under various interest rate scenarios (i.e., above and below 4%).

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
The current market conditions for an AAA client are 8% on a one-year dollar loan, and 8% fixed U.S. dollars for 9% fixed British pounds on a one-year dollar/pound currency swap. Let's consider a BBB client borrowing at (8 + m)% on a one-year dollar loan. The same client can enter a dollar/pound currency swap, paying (8 + µ)% fixed dollars and receiving 9% fixed pounds. Assume that the customer has a probability of p% to default within a year. In case of default, the bank knows that it will recover nothing on either transaction. The probability of default p (e.g., 5%) is known and independent of movements in interest and exchange rates. The spot exchange rate is S0 = 1 $/£.
Assuming that you can observe the prices of $/£ currency options, suggest some approach to determine the fair values of m and µ. (Assume that the bank has a large number of clients whose probabilities of default are independent; therefore, the bank can diversify away the uncertainty of default on this specific client.)
Assuming that you can observe the prices of $/£ currency options, suggest some approach to determine the fair values of m and µ. (Assume that the bank has a large number of clients whose probabilities of default are independent; therefore, the bank can diversify away the uncertainty of default on this specific client.)

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
A differential swap, or switch LIBOR swap, involves the LIBOR rates in two different currencies but with both legs denominated in the same currency. A Japanese insurance company engages in a differential swap whereby it receives the six-month Japanese yen LIBOR and pays the six-month U.S. dollar LIBOR plus 50 bp but with both legs denominated in yen. No principal is exchanged at the end. The current LIBOR for the yen and the dollar are 6% and 4%, respectively, and the principal is 100 million yen. Hence, the first swap payment will be based on a differential of 1.5% in yen [6% = (4%-0.5%)]. The current yield pick-up is 150 bp. There is no currency risk on this swap.
Provide some intuitive explanation for the pricing of such a swap, knowing that at the time, the dollar yield curve was very steep (long-term rates are much higher than short-term rates) and the yen yield curve was almost flat.
Provide some intuitive explanation for the pricing of such a swap, knowing that at the time, the dollar yield curve was very steep (long-term rates are much higher than short-term rates) and the yen yield curve was almost flat.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
A five-year currency swap involves two AAA borrowers and has been set at current market interest rates. The swap is for US$100 million against AUD 200 million at the current spot exchange rate of AUD/$ 2.00. The interest rates are 4% in U.S. dollars and 7% in Australian dollars, or annual swaps of $4 million for AUD 14 million. A year later, the interest rates have dropped to 3% in U.S. dollars and 6% in Australian dollars, and the exchange rate is now AUD/$ 1.9.
a. What should the market value of the swap be in the secondary market?
Assume now that the swap is instead a currency-interest rate swap whereby the dollar interest is set at LIBOR.
b. What would the market value of the currency-interest rate swap be if these conditions prevailed a year later?
a. What should the market value of the swap be in the secondary market?
Assume now that the swap is instead a currency-interest rate swap whereby the dollar interest is set at LIBOR.
b. What would the market value of the currency-interest rate swap be if these conditions prevailed a year later?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
The current dollar yield curve on the dollar international bond market is flat at 7% for top-quality borrowers. A company of good standing can issue plain-vanilla straight and floating-rate dollar bonds under the following conditions:
Bond A: Straight bond. Five-year straight dollar bond with a coupon of 7.25%.
Bond B: FRN. Five-year dollar FRN with a semiannual coupon set at LIBOR plus 0.25% and
a cap of 14%. The cap means that the coupon rate is limited to 14% even if the LIBOR passes 13.75%.
An investment banker proposes to a French company to issue bull and/or bear FRNs under the following conditions:
Bond C: Bull FRN. Five-year FRN with a semiannual coupon set at: 13.75% - LIBOR.
Bond D: Bear FRN. Five-year FRN with a semiannual coupon set at: 2 * LIBOR - 7% and a cap of 20.5%.
Coupons on all bonds cannot be negative. The investment bank also proposes a five-year floor option at 3.5%. This floor will pay to the French company the difference between 3.5% and LIBOR, if it is positive, or zero if LIBOR is above 3.5%. The cost of this floor is spread over the payment dates and
set at an annual 0.1%. The investment bank also proposes a five-year cap option at a strike of 13.75%. The cost of this cap is spread over the payment dates and set at an annual 0.05%. The company can also enter into a five-year interest rate swap at 7% fixed against LIBOR.
a. Explain why it would be attractive to the French company to issue these FRNs compared to current market conditions for plain-vanilla straight bonds and FRNs.
b. Find out the borrowing cost reduction that can be achieved by issuing bull notes compared to a fixed-coupon rate of 7.25%.
c. Find out the borrowing cost reduction that can be achieved by issuing bear notes compared to an FRN at LIBOR plus 0.25%.
Bond A: Straight bond. Five-year straight dollar bond with a coupon of 7.25%.
Bond B: FRN. Five-year dollar FRN with a semiannual coupon set at LIBOR plus 0.25% and
a cap of 14%. The cap means that the coupon rate is limited to 14% even if the LIBOR passes 13.75%.
An investment banker proposes to a French company to issue bull and/or bear FRNs under the following conditions:
Bond C: Bull FRN. Five-year FRN with a semiannual coupon set at: 13.75% - LIBOR.
Bond D: Bear FRN. Five-year FRN with a semiannual coupon set at: 2 * LIBOR - 7% and a cap of 20.5%.
Coupons on all bonds cannot be negative. The investment bank also proposes a five-year floor option at 3.5%. This floor will pay to the French company the difference between 3.5% and LIBOR, if it is positive, or zero if LIBOR is above 3.5%. The cost of this floor is spread over the payment dates and
set at an annual 0.1%. The investment bank also proposes a five-year cap option at a strike of 13.75%. The cost of this cap is spread over the payment dates and set at an annual 0.05%. The company can also enter into a five-year interest rate swap at 7% fixed against LIBOR.
a. Explain why it would be attractive to the French company to issue these FRNs compared to current market conditions for plain-vanilla straight bonds and FRNs.
b. Find out the borrowing cost reduction that can be achieved by issuing bull notes compared to a fixed-coupon rate of 7.25%.
c. Find out the borrowing cost reduction that can be achieved by issuing bear notes compared to an FRN at LIBOR plus 0.25%.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
You would like to protect your portfolio of British equity against a downward movement of the British stock market.
a. What are the relative advantages of stock index futures and options?
b. Should you prefer in-the-money or out-of-the-money options?
a. What are the relative advantages of stock index futures and options?
b. Should you prefer in-the-money or out-of-the-money options?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
A five-year currency swap involves two AAA borrowers and has been set at current market interest rates. The swap is for US$100 million against AUD 200 million at the current spot exchange rate of AUD/$ 2.00. The interest rates are 10% in U.S. dollars and 7% in Australian dollars, or annual swaps of US$10 million for AUD 14 million. A year later, the interest rates have dropped to 8% in U.S. dollars and 6% in Australian dollars, and the exchange rate is now AUD/$ 1.9.
a. What should the market value of the swap be in the secondary market?
Assume now that the swap is instead a currency-interest rate swap whereby the dollar interest is set at LIBOR.
b. What would the market value of the currency-interest rate swap be if these conditions prevailed a year later?
a. What should the market value of the swap be in the secondary market?
Assume now that the swap is instead a currency-interest rate swap whereby the dollar interest is set at LIBOR.
b. What would the market value of the currency-interest rate swap be if these conditions prevailed a year later?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
A small Dutch bank has the following balance sheet (in euros), based on historical or nominal values.
All assets and liabilities are denominated in euros. The bank borrows short-term on the Euro-currency market. The bank and its client are AAA quality. The net worth is calculated as the difference between the value of assets and liabilities. The current euro term structure for AAA borrowers is flat at 6.5%.
a. Value the balance sheet based on market value.
b. Compute the interest-rate sensitivity (duration) of the asset. Infer the interest rate sensitivity of the net worth of the bank. For example, how much would stockholders lose if euro interest rates moved up by 0.10%? (Assume that the interest rate sensitivity of an floating-rate note (FRN) is zero, as the coupon is reset to the market interest rate.)
c. The bank fears a rise in all euro interest rates. The current market conditions for interest rate swaps in euros are as follows:
With a maturity of three years are: 6.5% against Euribor.
With a maturity of five years are: 6.75% against Euribor.
What would you do to hedge this interest rate risk?
d. The next day, all interest rates move up to 8%. Value again the balance sheet, assuming that the floating-rate debt remains at 100% and that the bank has undertaken the swap that you recommended. Is the hedge perfect? Why?
All assets and liabilities are denominated in euros. The bank borrows short-term on the Euro-currency market. The bank and its client are AAA quality. The net worth is calculated as the difference between the value of assets and liabilities. The current euro term structure for AAA borrowers is flat at 6.5%.
a. Value the balance sheet based on market value.
b. Compute the interest-rate sensitivity (duration) of the asset. Infer the interest rate sensitivity of the net worth of the bank. For example, how much would stockholders lose if euro interest rates moved up by 0.10%? (Assume that the interest rate sensitivity of an floating-rate note (FRN) is zero, as the coupon is reset to the market interest rate.)
c. The bank fears a rise in all euro interest rates. The current market conditions for interest rate swaps in euros are as follows:
With a maturity of three years are: 6.5% against Euribor.
With a maturity of five years are: 6.75% against Euribor.
What would you do to hedge this interest rate risk?
d. The next day, all interest rates move up to 8%. Value again the balance sheet, assuming that the floating-rate debt remains at 100% and that the bank has undertaken the swap that you recommended. Is the hedge perfect? Why?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
A traditional interest rate swap has a notional capital of 100 and exchange LIBOR (the floating leg) against 6% (fixed leg). At maturity of the swap there is no capital exchange as the same notional capital of 100 is "exchanged" on both legs. Assume that the swap has a five-year maturity.
A company needs to create an immediate cash flow to offset an immediate loss and decides to use an amortizing swap. Its off-balance sheet items are accounted at their book or historical values. The floating leg is LIBOR, paid quarterly, with a notional capital of 100. The fixed leg also has a notional capital of 100, however, there is only an initial cash flow of X on the fixed leg of the amortizing swap and no other cash flow (zero coupons). Hence, there is no capital exchanged at maturity of the swap (capital identical on both legs). The swap is priced (the value of X is set) so that the initial swap value is zero.
The company enters the amortizing swap to pay floating and receive fixed. In other words, its cash flows on the swap are as follows:
Receive X at time 0.
Pays LIBOR every quarter for five years.
No cash flow at maturity.
a. Why is the amortizing swap interesting for this company, which wants to window-dress an immediate loss? How will it impact its future earnings?
b. The term structure is flat at 6%. What should be the "fair" value of X?
c. The company expects a loss of 10 million, what should be the notional capital of the amortizing swap that should be contracted?
d. Assume now that the company must value all off-balance sheet items at their market value. What would happen to the value of the swap immediately after the payment of X is received by the company? Are amortizing swaps useful in deferring losses with this accounting convention?
A company needs to create an immediate cash flow to offset an immediate loss and decides to use an amortizing swap. Its off-balance sheet items are accounted at their book or historical values. The floating leg is LIBOR, paid quarterly, with a notional capital of 100. The fixed leg also has a notional capital of 100, however, there is only an initial cash flow of X on the fixed leg of the amortizing swap and no other cash flow (zero coupons). Hence, there is no capital exchanged at maturity of the swap (capital identical on both legs). The swap is priced (the value of X is set) so that the initial swap value is zero.
The company enters the amortizing swap to pay floating and receive fixed. In other words, its cash flows on the swap are as follows:
Receive X at time 0.
Pays LIBOR every quarter for five years.
No cash flow at maturity.
a. Why is the amortizing swap interesting for this company, which wants to window-dress an immediate loss? How will it impact its future earnings?
b. The term structure is flat at 6%. What should be the "fair" value of X?
c. The company expects a loss of 10 million, what should be the notional capital of the amortizing swap that should be contracted?
d. Assume now that the company must value all off-balance sheet items at their market value. What would happen to the value of the swap immediately after the payment of X is received by the company? Are amortizing swaps useful in deferring losses with this accounting convention?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
LTCM observed the following ten-year swap spreads on July 1, 1998. You remember that U.S. dollar interest swaps (fixed rate against LIBOR three-month) are quoted as a spread over the Treasury yield (so the fixed rate on the swap is equal to the interest rate on Treasury bonds for the same maturity plus the quote spread). LTCM believes that the normal spread is 40 bp (basis points). The current spread of 80 bp is expected to converge back to normal in three months.
If you borrow securities, you have to deposit as collateral an equivalent amount of cash that is marked-to-market. For example, if you borrow a security that is worth 100, you have to deposit 100; if the value of the security increases to 110, you have to deposit 10 more. Swaps are also marked-to-market and free of default risk.![LTCM observed the following ten-year swap spreads on July 1, 1998. You remember that U.S. dollar interest swaps (fixed rate against LIBOR three-month) are quoted as a spread over the Treasury yield (so the fixed rate on the swap is equal to the interest rate on Treasury bonds for the same maturity plus the quote spread). LTCM believes that the normal spread is 40 bp (basis points). The current spread of 80 bp is expected to converge back to normal in three months. If you borrow securities, you have to deposit as collateral an equivalent amount of cash that is marked-to-market. For example, if you borrow a security that is worth 100, you have to deposit 100; if the value of the security increases to 110, you have to deposit 10 more. Swaps are also marked-to-market and free of default risk. a. What arbitrage using Treasury bonds and swaps could you put in place if you believe that the spread will revert back to its normal level? Be very precise and assume you do the above arbitrage for $100 million. How much of LTCM capital is invested in the arbitrage? b. Suppose that the spread is still at 80 bp on October 1, but that Treasury yields have moved up by 40 bp on October 1 (reset date for the floating leg). What is your gain/loss in dollars? [You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.] c. Other scenario: How much would you gain (from July 1) if Treasury yields do not move, but the spread reverts back to 40 bp three months later on October 1 (reset date for the floating leg)? [You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.]](https://storage.examlex.com/TB7821/11eac6a3_528e_f23b_af59_07e4183bb9f9_TB7821_00.jpg) a. What arbitrage using Treasury bonds and swaps could you put in place if you believe that the spread will revert back to its normal level? Be very precise and assume you do the above arbitrage for $100 million. How much of LTCM capital is invested in the arbitrage?
a. What arbitrage using Treasury bonds and swaps could you put in place if you believe that the spread will revert back to its normal level? Be very precise and assume you do the above arbitrage for $100 million. How much of LTCM capital is invested in the arbitrage?
b. Suppose that the spread is still at 80 bp on October 1, but that Treasury yields have moved
up by 40 bp on October 1 (reset date for the floating leg). What is your gain/loss in dollars?
[You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.]
c. Other scenario: How much would you gain (from July 1) if Treasury yields do not move, but
the spread reverts back to 40 bp three months later on October 1 (reset date for the floating leg)? [You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.]
If you borrow securities, you have to deposit as collateral an equivalent amount of cash that is marked-to-market. For example, if you borrow a security that is worth 100, you have to deposit 100; if the value of the security increases to 110, you have to deposit 10 more. Swaps are also marked-to-market and free of default risk.
![LTCM observed the following ten-year swap spreads on July 1, 1998. You remember that U.S. dollar interest swaps (fixed rate against LIBOR three-month) are quoted as a spread over the Treasury yield (so the fixed rate on the swap is equal to the interest rate on Treasury bonds for the same maturity plus the quote spread). LTCM believes that the normal spread is 40 bp (basis points). The current spread of 80 bp is expected to converge back to normal in three months. If you borrow securities, you have to deposit as collateral an equivalent amount of cash that is marked-to-market. For example, if you borrow a security that is worth 100, you have to deposit 100; if the value of the security increases to 110, you have to deposit 10 more. Swaps are also marked-to-market and free of default risk. a. What arbitrage using Treasury bonds and swaps could you put in place if you believe that the spread will revert back to its normal level? Be very precise and assume you do the above arbitrage for $100 million. How much of LTCM capital is invested in the arbitrage? b. Suppose that the spread is still at 80 bp on October 1, but that Treasury yields have moved up by 40 bp on October 1 (reset date for the floating leg). What is your gain/loss in dollars? [You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.] c. Other scenario: How much would you gain (from July 1) if Treasury yields do not move, but the spread reverts back to 40 bp three months later on October 1 (reset date for the floating leg)? [You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.]](https://storage.examlex.com/TB7821/11eac6a3_528e_f23b_af59_07e4183bb9f9_TB7821_00.jpg) a. What arbitrage using Treasury bonds and swaps could you put in place if you believe that the spread will revert back to its normal level? Be very precise and assume you do the above arbitrage for $100 million. How much of LTCM capital is invested in the arbitrage?
a. What arbitrage using Treasury bonds and swaps could you put in place if you believe that the spread will revert back to its normal level? Be very precise and assume you do the above arbitrage for $100 million. How much of LTCM capital is invested in the arbitrage?b. Suppose that the spread is still at 80 bp on October 1, but that Treasury yields have moved
up by 40 bp on October 1 (reset date for the floating leg). What is your gain/loss in dollars?
[You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.]
c. Other scenario: How much would you gain (from July 1) if Treasury yields do not move, but
the spread reverts back to 40 bp three months later on October 1 (reset date for the floating leg)? [You only need to provide a rough estimate assuming that the sensitivity (duration) on the Treasury bond and fixed leg of the swap is equal to 10.]

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
You're a banker. A client wishes to buy a guaranteed note with a 100% indexation to the stock index's growth. In other words, he doesn't want any coupon but requires 100% of the index growth. You wonder about the maturity of such a note. You check the prices of various index calls traded on the market for different maturities. Their strike is the current index level and their price is expressed as a percentage of this level. (For instance if the CAC is worth 3,000, the strike is 3,000 and the one-year maturity call trades at 11% of 3,000. You also check the price of a zero-coupon in percentage for various maturities. The following graph shows, for each maturity, the price of the option, that of the zero-coupon, and 100%-zero.  a. What is the maturity of the guaranteed note (coupon =0%, indexation =100%)? Justify.
a. What is the maturity of the guaranteed note (coupon =0%, indexation =100%)? Justify.
b. If as a banker, you want to make a profit, should you lengthen or shorten the maturity of that note? Explain why.
c. Everything remaining constant (that is, same volatility and interest rate), should the maturity of the guaranteed note be shorter or longer if the index pays a low dividend rather than a high one? Why?
 a. What is the maturity of the guaranteed note (coupon =0%, indexation =100%)? Justify.
a. What is the maturity of the guaranteed note (coupon =0%, indexation =100%)? Justify.b. If as a banker, you want to make a profit, should you lengthen or shorten the maturity of that note? Explain why.
c. Everything remaining constant (that is, same volatility and interest rate), should the maturity of the guaranteed note be shorter or longer if the index pays a low dividend rather than a high one? Why?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
Titi, a Japanese company, issued a six-year international bond in dollars convertible into shares of the company. At time of issue, the long-term bond yield on straight dollar bonds was 10% for such an issuer. Instead, Titi issued bonds at 8%. Each $1,000 par bond is convertible into 100 shares of Titi. At time of issue, the stock price of Titi is 1,600 yen, and the exchange rate is 100 yen = 0.5 dollars ($/¥ = 0.005, ¥/$ = 200).
a. Why can the bond be issued with a yield of only 8%, below the market rate for straight dollar bonds?
b. What would happen if:
The stock price of Titi increases?
The yen appreciates?
The market interest rate of dollar bonds drops?
A year later, the new market conditions are as follows:
The yield on straight dollar bonds of similar quality has risen from 10% to 11%.
Titi stock price has moved up to ¥ 2,000.
The exchange rate is $/¥ 0.006.
c. What would be a minimum price for the Titi convertible bond?
d. Could you try to assess the theoretical value of this convertible bond as a package of other securities, such as straight bonds issued by Titi, options or warrants on the yen value of Titi stock, and futures and options on the dollar/yen exchange rate?
a. Why can the bond be issued with a yield of only 8%, below the market rate for straight dollar bonds?
b. What would happen if:
The stock price of Titi increases?
The yen appreciates?
The market interest rate of dollar bonds drops?
A year later, the new market conditions are as follows:
The yield on straight dollar bonds of similar quality has risen from 10% to 11%.
Titi stock price has moved up to ¥ 2,000.
The exchange rate is $/¥ 0.006.
c. What would be a minimum price for the Titi convertible bond?
d. Could you try to assess the theoretical value of this convertible bond as a package of other securities, such as straight bonds issued by Titi, options or warrants on the yen value of Titi stock, and futures and options on the dollar/yen exchange rate?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
Guaranteed note.
You are a young banker offering a client to issue a guaranteed note. The yield curve is flat at 9% for each maturity. Options on the stock index are offered by banks. A at-the-money call with a two-year maturity trades at 12% of the index value, whereas a three-year call is worth 15% of the index.
You wonder about the characteristics of the bond. If you offer a high coupon, the indexation will be low. Therefore, you decide to compute the indexation levels in accordance to the current market conditions for maturities of two and three years and coupon levels of 0%, 2%, and 5%.
You are a young banker offering a client to issue a guaranteed note. The yield curve is flat at 9% for each maturity. Options on the stock index are offered by banks. A at-the-money call with a two-year maturity trades at 12% of the index value, whereas a three-year call is worth 15% of the index.
You wonder about the characteristics of the bond. If you offer a high coupon, the indexation will be low. Therefore, you decide to compute the indexation levels in accordance to the current market conditions for maturities of two and three years and coupon levels of 0%, 2%, and 5%.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
Strumpf Ltd. decides to issue a convertible bond with a maturity of two years. Each bond is issued with a nominal value of £ 100 and an annual coupon C; of course, C has to be determined. Each bond can be redeemed for £ 100 or converted into one share of Strumpf at the option of the bondholder.
The current stock price of Strumpf is £90. The yield curve for an issuer like Strumpf is flat at 6%. Barings is ready to issue long-term options on Strumpf shares. The premiums on calls with one-year and two-year expirations are given below:
 a. American-type calls are more expensive than European-type calls. Is it reasonable?
a. American-type calls are more expensive than European-type calls. Is it reasonable?
b. Assume that the bond can only be converted at maturity, after payment of the second coupon. What should be the fair coupon rate C, consistent with the above market conditions?
c. Assume that the bond is issued with the coupon rate determined above. The yield curve suddenly moves from 6% to 6.1% and the option premiums stay the same. What should be the new market price of the convertible bond?
d. Assume now that the bond can be converted on two dates (rather than one as above). These dates are the first year (right after the first coupon payment) and the second year as above. It is not possible to convert the two-year bond at any other date. Is it possible to construct an arbitrage portfolio allowing to price the fair coupon C with the above data? Be precise in your explanation and state what type of options you would need to price the bond.
The current stock price of Strumpf is £90. The yield curve for an issuer like Strumpf is flat at 6%. Barings is ready to issue long-term options on Strumpf shares. The premiums on calls with one-year and two-year expirations are given below:
 a. American-type calls are more expensive than European-type calls. Is it reasonable?
a. American-type calls are more expensive than European-type calls. Is it reasonable?b. Assume that the bond can only be converted at maturity, after payment of the second coupon. What should be the fair coupon rate C, consistent with the above market conditions?
c. Assume that the bond is issued with the coupon rate determined above. The yield curve suddenly moves from 6% to 6.1% and the option premiums stay the same. What should be the new market price of the convertible bond?
d. Assume now that the bond can be converted on two dates (rather than one as above). These dates are the first year (right after the first coupon payment) and the second year as above. It is not possible to convert the two-year bond at any other date. Is it possible to construct an arbitrage portfolio allowing to price the fair coupon C with the above data? Be precise in your explanation and state what type of options you would need to price the bond.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
Digital options: Digital (or binary) options can only have two payoffs at maturity. If the strike condition set in the option is met, the buyer will receive the full prespecified payoff. If not, the buyer receives no payoff. This is different from a traditional option where there exists an infinite number of payoffs. For example, we could have a digital option on the French CAC index, stating that the option buyer will get €200 if the CAC index is above 4,000 at expiration and zero otherwise. On this digital option, the buyer will get exactly 200 as soon as the CAC index is above the 4,000 level at expiration, whether it be 4,001, 4,100, or 5,000.
a. Draw the profit and loss curve at expiration as a function of the CAC index for these two options:
Traditional call on the CAC index: Exercise price: 4,000; premium: 40.
Digital call on the CAC index: Exercise price: 4,000; payoff if exercised: 200; premium: 40.
b. What are the relative advantages of the two options?
c. Assume that the volatility of the French stock market increases suddenly. Should the premium on the digital call increase more (or less) than the premium on the traditional call?
a. Draw the profit and loss curve at expiration as a function of the CAC index for these two options:
Traditional call on the CAC index: Exercise price: 4,000; premium: 40.
Digital call on the CAC index: Exercise price: 4,000; payoff if exercised: 200; premium: 40.
b. What are the relative advantages of the two options?
c. Assume that the volatility of the French stock market increases suddenly. Should the premium on the digital call increase more (or less) than the premium on the traditional call?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
The Kingdom of Papou issues a very-bull bond with a coupon equal to:
14.6 - 2 * LIBOR.
Of course, the coupon cannot be negative.
The Kingdom could have issued a FRN at LIBOR + ¼ %, or a straight bond at 5.30%.
The current market conditions for swaps are 5% against LIBOR.
You could also trade in caps and floors with different exercise prices (these are levels of interest rates). The premium are paid annually.
a. You are a buyer of this very-bull bond. Tell us what it is equivalent to, in terms of buying/selling: FRN, straight bonds, caps or floors.
b. Assume that the Kingdom actually wanted to issue a straight bond (fixed coupon). The bank will put in place a "de-mining" portfolio with swaps and options so that this very-bull bond plus the "de-mining" portfolio is equivalent to a straight bond. What is exactly the "de-mining" portfolio? (Be very precise and tell us if the Kingdom must pay fixed, receive LIBOR or vice versa, etc.)
c. What is the cost advantage for the Kingdom compared to issuing bonds at 5.30%?
d. Same question assuming that the Kingdom wanted to issue an FRN at LIBOR +¼%?
14.6 - 2 * LIBOR.
Of course, the coupon cannot be negative.
The Kingdom could have issued a FRN at LIBOR + ¼ %, or a straight bond at 5.30%.
The current market conditions for swaps are 5% against LIBOR.
You could also trade in caps and floors with different exercise prices (these are levels of interest rates). The premium are paid annually.
a. You are a buyer of this very-bull bond. Tell us what it is equivalent to, in terms of buying/selling: FRN, straight bonds, caps or floors.
b. Assume that the Kingdom actually wanted to issue a straight bond (fixed coupon). The bank will put in place a "de-mining" portfolio with swaps and options so that this very-bull bond plus the "de-mining" portfolio is equivalent to a straight bond. What is exactly the "de-mining" portfolio? (Be very precise and tell us if the Kingdom must pay fixed, receive LIBOR or vice versa, etc.)
c. What is the cost advantage for the Kingdom compared to issuing bonds at 5.30%?
d. Same question assuming that the Kingdom wanted to issue an FRN at LIBOR +¼%?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
In 1990, the French bank, BNP, issued exchangeable bonds denominated in French francs (FF). These are bonds issued for FF 100 on April 1, 1990, with an annual coupon of FF 5, plus an exchange right. The bonds can be redeemed for FF 100 on April 1, 1996. The right can be exchanged on
April 1, 1991, with payment of an additional FF 100, for another bond identical to the old bond (annual coupon of FF 5 and redeemed for FF 100 on April 1, 1996). If you exercise your right, you will have paid an additional FF 100 on April 1, 1991, but you will then hold two BNP bonds with maturity in 1996.
a. Under what scenario would you exercise the exchange right (exchange the right plus FF 100 for an additional bond) on April 1, 1991? What is the attraction of such an exchangeable bond for investors?
b. On April 1, 1990, the yield curve is flat at 6%. You can buy a call on a five-year bond with a coupon of 5%. The call has a strike price of 100% and expires on April 1, 1991. Its premium is 2%. Construct a replication portfolio to determine at what price the exchangeable bond can be issued by BNP.
April 1, 1991, with payment of an additional FF 100, for another bond identical to the old bond (annual coupon of FF 5 and redeemed for FF 100 on April 1, 1996). If you exercise your right, you will have paid an additional FF 100 on April 1, 1991, but you will then hold two BNP bonds with maturity in 1996.
a. Under what scenario would you exercise the exchange right (exchange the right plus FF 100 for an additional bond) on April 1, 1991? What is the attraction of such an exchangeable bond for investors?
b. On April 1, 1990, the yield curve is flat at 6%. You can buy a call on a five-year bond with a coupon of 5%. The call has a strike price of 100% and expires on April 1, 1991. Its premium is 2%. Construct a replication portfolio to determine at what price the exchangeable bond can be issued by BNP.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
Bank PAPOUF decides to issue two bonds and wonders what the fair interest rate on these bonds should be:
A. A one-year currency option bond. The bond is issued in dollars with a face value of $100. The bondholder can choose to have the coupon and principal paid in dollars or in SFr, at a specified exchange rate of SFr/$ = 2, that is, receive either $100 or SFr 200 as principal repayment, and receive either $C or SFr 2C as interest if C is the coupon set in dollars. The coupon rate is
c = C/100.
B. A two-year currency option bond. The bond is issued in dollars, with a face value of $100 and pays an annual coupon C'. The bondholder can choose to have the coupons and principal paid in dollars or in SFr, at a specified exchange rate of SFr/$ = 2, that is, receive either $100 or SFr 200 as principal repayment, and receive either $C' or SFr 2C' as interest, if C' is the coupon set in dollars. The coupon rate is c'= C'/100.
Current market conditions are given below:
Interest Rates 1-Year 2-Year
Zero-coupon rates
US$ 8% 8%
SFr 4% 4%
Spot exchange rate: SFr/$= 2
Currency options:
SFr call, strike price 50 U.S. cents, expiration one year: 2 U.S. cents.
SFr call, strike price 50 U.S. cents, expiration two years: 5 U.S. cents.
a. Compute the coupon C on Bond A that would be consistent with market conditions at time of issue.
b. Compute the coupon C' on Bond B that would be consistent with market conditions at time of issue.
A. A one-year currency option bond. The bond is issued in dollars with a face value of $100. The bondholder can choose to have the coupon and principal paid in dollars or in SFr, at a specified exchange rate of SFr/$ = 2, that is, receive either $100 or SFr 200 as principal repayment, and receive either $C or SFr 2C as interest if C is the coupon set in dollars. The coupon rate is
c = C/100.
B. A two-year currency option bond. The bond is issued in dollars, with a face value of $100 and pays an annual coupon C'. The bondholder can choose to have the coupons and principal paid in dollars or in SFr, at a specified exchange rate of SFr/$ = 2, that is, receive either $100 or SFr 200 as principal repayment, and receive either $C' or SFr 2C' as interest, if C' is the coupon set in dollars. The coupon rate is c'= C'/100.
Current market conditions are given below:
Interest Rates 1-Year 2-Year
Zero-coupon rates
US$ 8% 8%
SFr 4% 4%
Spot exchange rate: SFr/$= 2
Currency options:
SFr call, strike price 50 U.S. cents, expiration one year: 2 U.S. cents.
SFr call, strike price 50 U.S. cents, expiration two years: 5 U.S. cents.
a. Compute the coupon C on Bond A that would be consistent with market conditions at time of issue.
b. Compute the coupon C' on Bond B that would be consistent with market conditions at time of issue.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
You are a young investment banker considering the issuance of a guaranteed note with stock index participation for a client. The current yield curve is flat at 8% for all maturities. Long-term at-the-money options on the stock market index are traded by banks. Two-year at-the-money calls trade
at 17.84% of the index value; three-year at-the-money calls trade at 20% of the index value. You
are hesitant about the terms to set in the structured note. You know that if you guarantee a higher
coupon rate, the level of participation in the stock appreciation will be less. Your boss asks you to compute the "fair" participation rate that would be feasible for various guaranteed coupon rates and maturities. In other words, based on the current market conditions (as described above), estimate the participation rates that are feasible with a maturity of two or three years, and a coupon rate of: 0%, 1%, 2%, 3%, 5%, and 7%.
at 17.84% of the index value; three-year at-the-money calls trade at 20% of the index value. You
are hesitant about the terms to set in the structured note. You know that if you guarantee a higher
coupon rate, the level of participation in the stock appreciation will be less. Your boss asks you to compute the "fair" participation rate that would be feasible for various guaranteed coupon rates and maturities. In other words, based on the current market conditions (as described above), estimate the participation rates that are feasible with a maturity of two or three years, and a coupon rate of: 0%, 1%, 2%, 3%, 5%, and 7%.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


