Deck 13: The Nature of Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/97
Play
Full screen (f)
Deck 13: The Nature of Probability
1
All the cows in a certain herd are white-faced. The probability that a white-faced calf will be born by mating with a certain bull is 0.8. Suppose 2 cows are bred to the same bull. Find the probability, that no white-faced calves will be born.
Please round your answer to four decimal places.
P = __________
Please round your answer to four decimal places.
P = __________
0.0400
2
Find the binomial probability.
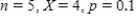
Round your answer to five significant digits.
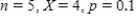
Round your answer to five significant digits.
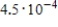
3
Suppose you are taking a true-false test with ten questions. If you guess at the answers on this test, find the probability of getting fewer than nine correct answers.
A) 0.9944
B) 0.9928
C) 0.9868
D) 0.9935
E) 0.9893
A) 0.9944
B) 0.9928
C) 0.9868
D) 0.9935
E) 0.9893
0.9893
4
Suppose that research has shown that the probability that a missile penetrates enemy defenses and reaches its target is 0.1. Find the smallest number of identical missiles that are necessary in order to be 90% certain of hitting the target at least once.
A) 27
B) 22
C) 20
D) 21
E) 19
A) 27
B) 22
C) 20
D) 21
E) 19

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose the National League team has a probability of 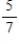 of winning a World Series game and the American League team has a probability of
of winning a World Series game and the American League team has a probability of 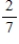 . The series is over as soon as one team wins four games. Find the probability that the series is over in seven games. Please round your answer to four decimal places.
. The series is over as soon as one team wins four games. Find the probability that the series is over in seven games. Please round your answer to four decimal places.
P = __________
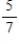 of winning a World Series game and the American League team has a probability of
of winning a World Series game and the American League team has a probability of 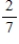 . The series is over as soon as one team wins four games. Find the probability that the series is over in seven games. Please round your answer to four decimal places.
. The series is over as soon as one team wins four games. Find the probability that the series is over in seven games. Please round your answer to four decimal places.
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
6
Find the binomial probability. 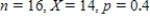
A)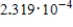
B)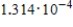
C)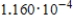
D)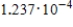
E)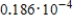
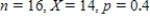
A)
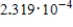
B)
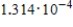
C)
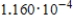
D)
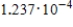
E)
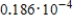

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose you are taking a true-false test with ten questions. If you guess at the answers on this test, find the probability of getting fewer than three correct answers. Please round your answer to four decimal places.
P = __________
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
8
Find the probability of obtaining exactly four threes on six rolls of a fair die. Please round your answer to three decimal places.
P = __________
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
9
Lymnozyme cures most infections in Koi fish caused by bacteria; in fact, it has been shown to be 98% effective if used according to the directions. If 14 Koi with a bacterial infection are treated, what is the probability that 13 of the fish are cured? Please round your answer to four decimal places.
P = __________
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
10
Find the probability of obtaining exactly two threes on four rolls of a fair die.
A) 0.559
B) 0.243
C) 0.068
D) 0.116
E) 0.131
A) 0.559
B) 0.243
C) 0.068
D) 0.116
E) 0.131

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
11
A researcher chooses three leaves from a target environment and classifies each sample as fungus-free or contaminated. Suppose that a leaf has a probability of 0.4 of being infected. Find the probability, that two leaves infected.
A) 0.490
B) 0.181
C) 0.314
D) 0.144
E) 0.288
A) 0.490
B) 0.181
C) 0.314
D) 0.144
E) 0.288

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
12
Lymnozyme cures most infections in Koi fish caused by bacteria; in fact, it has been shown to be 98% effective if used according to the directions. If 11 Koi with a bacterial infection are treated, what is the probability that 10 of the fish are cured?
A) 0.1788
B) 0.1798
C) 0.1973
D) 0.9481
E) 0.1767
A) 0.1788
B) 0.1798
C) 0.1973
D) 0.9481
E) 0.1767

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
13
Lymnozyme cures most infections in Koi fish caused by bacteria; in fact, it has been shown to be 91% effective if used according to the directions. If 5 Koi with a bacterial infection are treated, what is the probability that 4 of the fish are cured?
A) 0.3086
B) 0.3261
C) 0.8837
D) 0.3076
E) 0.3055
A) 0.3086
B) 0.3261
C) 0.8837
D) 0.3076
E) 0.3055

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
14
In a certain office, seven men determine who will pay for coffee by each flipping a coin. If one of them has an outcome that is different from the other six, he must pay for the coffee. What is the probability that in any play of the game there will be an "odd man out"? Please round your answer to four decimal places.
P = __________
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that research has shown that the probability that a missile penetrates enemy defenses and reaches its target is 0.2. Find the smallest number of identical missiles that are necessary in order to be 50% certain of hitting the target at least once.
__________ missiles
__________ missiles

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
16
A researcher chooses three leaves from a target environment and classifies each sample as fungus-free or contaminated. Suppose that a leaf has a probability of 0.4 of being infected. Find the probability, that three leaves are infected. Please round your answer to three decimal places.
P = __________
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
17
Lymnozyme cures most infections in Koi fish caused by bacteria; in fact, it has been shown to be 96% effective if used according to the directions. If 7 Koi with a bacterial infection are treated, what is the probability that 6 of the fish are cured? Please round your answer to four decimal places.
P = __________
P = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
18
In a certain office, six men determine who will pay for coffee by each flipping a coin. If one of them has an outcome that is different from the other five, he must pay for the coffee. What is the probability that in any play of the game there will be an "odd man out"?
A) 0.1875
B) 0.1125
C) 0.0188
D) 0.1313
E) 0.0750
A) 0.1875
B) 0.1125
C) 0.0188
D) 0.1313
E) 0.0750

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose the National League team has a probability of 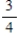 of winning a World Series game and the American League team has a probability of
of winning a World Series game and the American League team has a probability of 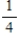 . The series is over as soon as one team wins four games. Find the probability that the series is over in seven games.
. The series is over as soon as one team wins four games. Find the probability that the series is over in seven games.
A) 0.1518
B) 0.2718
C) 0.1318
D) 0.1438
E) 0.1294
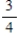 of winning a World Series game and the American League team has a probability of
of winning a World Series game and the American League team has a probability of 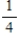 . The series is over as soon as one team wins four games. Find the probability that the series is over in seven games.
. The series is over as soon as one team wins four games. Find the probability that the series is over in seven games. A) 0.1518
B) 0.2718
C) 0.1318
D) 0.1438
E) 0.1294

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
20
All the cows in a certain herd are white-faced. The probability that a white-faced calf will be born by mating with a certain bull is 0.7. Suppose 6 cows are bred to the same bull. Find the probability, that no white-faced calves will be born.
A) 0.0004
B) 0.0008
C) 0.0023
D) 0.0007
E) 0.0051
A) 0.0004
B) 0.0008
C) 0.0023
D) 0.0007
E) 0.0051

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose that in an assortment of 20 calculators, there are 5 with defective switches. Draw with and without replacement. If two machines are selected at random, what is the probability that both have defective switches?
probability with replacement = __________
probability without replacement = __________
probability with replacement = __________
probability without replacement = __________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose a slot machine has three independent wheels as shown in the figure.
Find the probability P(3 bar). Give your answer to four decimal places, if required.

Find the probability P(3 bar). Give your answer to four decimal places, if required.


Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
23
What is the probability that two people in your class (assume a class of 30 students) have the same birthday?
A) 70.6%
B) 73.7%
C) 0.1%
D) 65.2%
E) 29.4%
A) 70.6%
B) 73.7%
C) 0.1%
D) 65.2%
E) 29.4%

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
24
Find the requested probability. 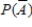 if
if 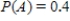
A)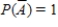
B)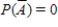
C) 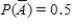
D) 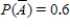
E) 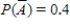
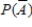 if
if 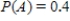
A)
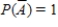
B)
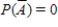
C)
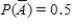
D)
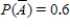
E)
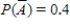

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
25
A game consists of removing a card from a deck of 52 cards. If the card is a face card, you win $3 and the game is over. If it is not a face card, remove another card. If that one is a face card, you win $3. Repeat the process again, and then again (for a total of 4 times). If you have not removed any face card, then you lose the game, and must pay $3. Should you play this game?
A) no
B) yes
A) no
B) yes

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
26
A game consists of removing a card from a deck of 52 cards. If the card is a face card, you win $2 and the game is over. If it is not a face card, remove another card. If that one is a face card, you win $2. Repeat the process again, and then again (for a total of 4 times). If you have not removed any face card, then you lose the game, and must pay $2. Should you play this game?
Answer yes or no.
Answer yes or no.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose a slot machine has three independent wheels as shown in the figure.
Find the probability P(3 plum). Round your answer to four decimal places if necessary.

A) 0
B) 0.05
C) 0.0045
D) 0.002
E) 0.01
Find the probability P(3 plum). Round your answer to four decimal places if necessary.

A) 0
B) 0.05
C) 0.0045
D) 0.002
E) 0.01

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
28
Suppose events A, B, and C are independent and 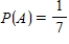 ,
, 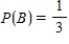 ,
, 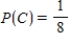 .
.
Find the probability of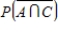 .
.
A)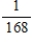
B)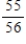
C)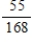
D)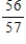
E)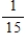
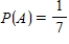 ,
, 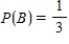 ,
, 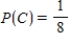 .
. Find the probability of
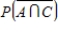 .
.
A)
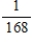
B)
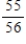
C)
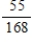
D)
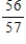
E)
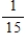

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose events A, B, and C are independent and 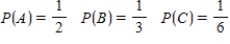
Find the probability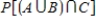 .
.
A)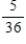
B)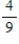
C)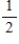
D)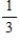
E)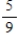
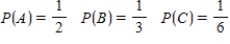
Find the probability
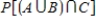 .
.
A)
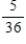
B)
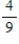
C)
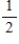
D)
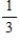
E)
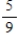

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose events A, B, and C are independent and 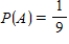 ,
, 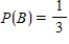 ,
, 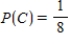 .
.
Find the probability of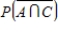 .
.
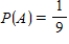 ,
, 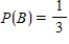 ,
, 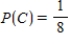 .
.
Find the probability of
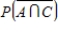 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose a die is rolled twice and let
A = {first toss is a prime}
B = {first toss is 2}
C = {second toss is a 3}
D = {second toss is 2}
Find the probability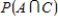 .
.
A = {first toss is a prime}
B = {first toss is 2}
C = {second toss is a 3}
D = {second toss is 2}
Find the probability
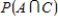 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
32
Suppose that in an assortment of 6 calculators, there are 3 with defective switches. Draw with and without replacement. If two machines are selected at random, what is the probability that both have defective switches?
A) with :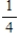 , without :
, without : 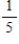
B) both :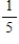
C) with :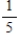 , without :
, without : 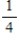
D) both :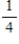
E) none of these
A) with :
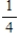 , without :
, without : 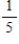
B) both :
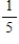
C) with :
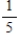 , without :
, without : 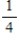
D) both :
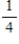
E) none of these

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
33
What is the probability of obtaining at least one head when a coin is flipped six times?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
34
Suppose events A, B, and C are independent and 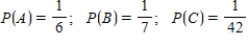
Find the probability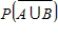 .
.
A)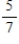
B)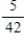
C)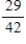
D)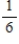
E)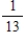
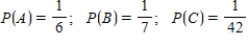
Find the probability
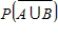 .
.
A)
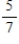
B)
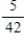
C)
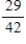
D)
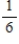
E)
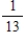

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
35
What is the probability that two people in your class (assume a class of 30 students) have the same birthday? Please, express your answer to 0.1%.
__________%
__________%

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
36
What is the probability of obtaining at least one head when a coin is flipped four times?
A)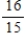
B)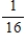
C)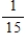
D)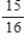
E)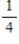
A)
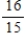
B)
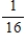
C)
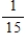
D)
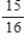
E)
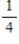

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following is more probable?
A. Flipping a coin 4 times and obtaining at least 3 heads.
B. Flipping a coin 5 times and obtaining at least 3 heads.
A) A
B) B
C) same
D) cannot tell
A. Flipping a coin 4 times and obtaining at least 3 heads.
B. Flipping a coin 5 times and obtaining at least 3 heads.
A) A
B) B
C) same
D) cannot tell

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose events A, B, and C are independent and
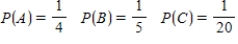
Find the probability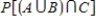 .
.
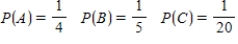
Find the probability
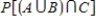 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose a die is rolled twice and let
A = {first toss is a prime}
B = {first toss is 5}
C = {second toss is a 6}
D = {second toss is 5}
Find the probability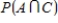 .
.
A)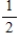
B)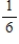
C)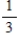
D)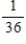
E)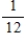
A = {first toss is a prime}
B = {first toss is 5}
C = {second toss is a 6}
D = {second toss is 5}
Find the probability
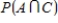 .
.
A)
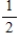
B)
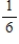
C)
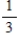
D)
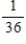
E)
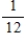

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose events A, B, and C are independent and
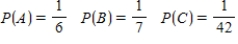
Find the probability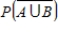 .
.
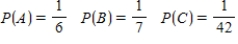
Find the probability
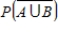 .
.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
41
A sorority has 12 members, 4 of whom are full members and 8 are pledges. Two persons are selected at random from the membership list of the sorority. Find the probability: the second person selected is a pledge.
A)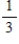
B)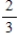
C)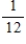
D)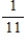
E)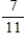
A)
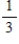
B)
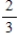
C)
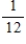
D)
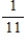
E)
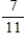

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
42
The probability of drawing a club from a deck of cards is 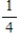 ; what are the odds in favor of drawing a club?
; what are the odds in favor of drawing a club?
A) 1 to 4
B) 3 to 1
C) 1 to 5
D) 2 to 3
E) 1 to 3
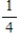 ; what are the odds in favor of drawing a club?
; what are the odds in favor of drawing a club? A) 1 to 4
B) 3 to 1
C) 1 to 5
D) 2 to 3
E) 1 to 3

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
43
A single card is drawn from a standard deck of cards. Find the probabilities if the given information is known about the chosen card. A face card is a jack, queen, or king. 
A) 0
B)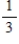
C) 1
D)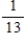
E)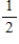

A) 0
B)
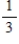
C) 1
D)
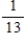
E)
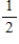

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
44
A single card is drawn from a standard deck of cards. Find the probabilities if the given information is known about the chosen card. A face card is a jack, queen, or king.



Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
45
A sorority has 36 members, 28 of whom are full members and 8 are pledges. Two persons are selected at random from the membership list of the sorority. Find the probability: the second person selected is a pledge.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
46
Two cards are drawn from a deck of cards. Find the requested probability.
The second card drawn is a club if the first card drawn was a club.
The second card drawn is a club if the first card drawn was a club.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
47
Which of the following is more probable? Answer A, B, or same.
A) Flipping a coin 3 times and obtaining at least 2 heads.
B) Flipping a coin 4 times and obtaining at least 2 heads.
A) Flipping a coin 3 times and obtaining at least 2 heads.
B) Flipping a coin 4 times and obtaining at least 2 heads.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
48
A sorority has 20 members, 12 of whom are full members and 8 are pledges. Two persons are selected at random from the membership list of the sorority. Find the probability: the first person selected is a pledge.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
49
Two cards are drawn from a standard deck of cards, and one of the two cards is noted and removed. Find the probability of drawing the second card, given the information about the removed card.
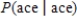
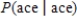

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
50
Two cards are drawn from a standard deck of cards, and one of the two cards is noted and removed. Find the probability of drawing the second card, given the information about the removed card. 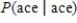
A)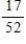
B)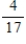
C)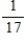
D)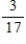
E)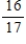
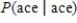
A)
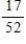
B)
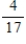
C)
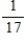
D)
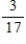
E)
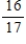

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
51
Find the requested probability. Give your answer to two decimal places, if required.
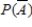 if
if 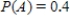
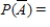 __________
__________
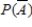 if
if 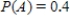
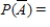 __________
__________
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
52
A sorority has 27 members, 21 of whom are full members and 6 are pledges. Two persons are selected at random from the membership list of the sorority. Find the probability: the first person selected is a pledge.
A)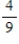
B)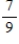
C)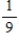
D)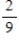
E)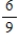
A)
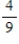
B)
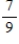
C)
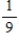
D)
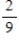
E)
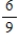

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
53
Choose a natural number between 1 and 100, inclusive. What is the probability that the number chosen is not a multiple of 4?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
54
Use estimation to select the best response. Do not calculate.
The probability of correctly guessing a telephone number is about
A) 1 out of 100
B) 1 out of 10
C) 1 out of 1,000,000
D) 1 out of 10,000
E) 1 out of 1,000
The probability of correctly guessing a telephone number is about
A) 1 out of 100
B) 1 out of 10
C) 1 out of 1,000,000
D) 1 out of 10,000
E) 1 out of 1,000

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose a pair of dice are rolled. Consider the sum of the numbers on the top of the dice and find the probability.
7, given that at least one die came up 2
7, given that at least one die came up 2

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose that you roll two dice. You will be paid $5 if you roll a double. You will not receive anything for any other outcome. How much should you be willing to pay for the privilege of rolling the dice?
A) $0.69
B) $0.14
C) $0.28
D) $0.83
E) $5.00
A) $0.69
B) $0.14
C) $0.28
D) $0.83
E) $5.00

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
57
The probability of drawing a diamond from a deck of cards is 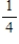 ; what are the odds in favor of drawing a diamond?
; what are the odds in favor of drawing a diamond?
The odds are __________ to __________.
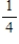 ; what are the odds in favor of drawing a diamond?
; what are the odds in favor of drawing a diamond?
The odds are __________ to __________.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
58
Choose a natural number between 1 and 100, inclusive. What is the probability that the number chosen is not a multiple of 5?
A)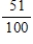
B)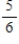
C)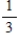
D)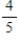
E)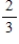
A)
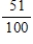
B)
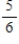
C)
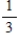
D)
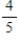
E)
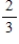

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
59
Two cards are drawn from a deck of cards. Find the requested probability.
The second card drawn is a spade if the first card drawn was a spade.
A)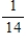
B)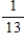
C)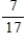
D)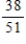
E)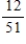
The second card drawn is a spade if the first card drawn was a spade.
A)
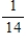
B)
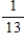
C)
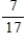
D)
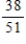
E)
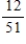

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
60
Suppose a pair of dice are rolled. Consider the sum of the numbers on the top of the dice and find the probability.
8, given that at least one die came up 3
A)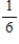
B)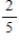
C)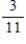
D)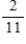
E)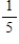
8, given that at least one die came up 3
A)
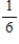
B)
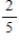
C)
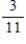
D)
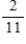
E)
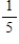

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
61
An oil-drilling company knows that it costs $65,000 to sink a test well. If oil is hit, the income for the drilling company will be $550,000. If only natural gas is hit, the income will be $428,373. If nothing is hit, there will be no income. If the probability of hitting oil is 1/65 and if the probability of hitting gas is 1/35, what is the expectation for the drilling company? Should the company sink the test well?
A) - $55,216; should dig
B) $44,299; should dig
C) - $44,299; should dig
D) - $44,299; should not dig
E) - $42,695; should not dig
A) - $55,216; should dig
B) $44,299; should dig
C) - $44,299; should dig
D) - $44,299; should not dig
E) - $42,695; should not dig

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
62
What is the expectation for the $1 five-number bet on a U.S. roulette wheel?
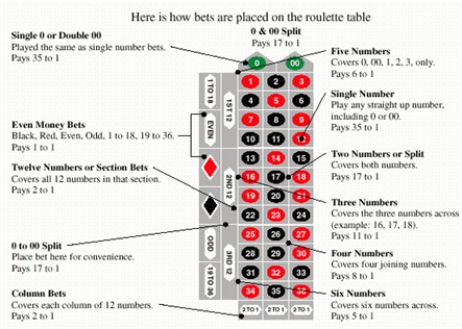
$__________

$__________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
63
A box contains one each of $2, $8, $40, $65, and $100 bills. You reach in and withdraw one bill. What is the expected value? Please round your answer to the nearest dollar.
$__________
$__________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
64
Use estimation to find the expected value. Do not calculate.
The expected value of playing a $1 game of blackjack is $0.04, find the netted value after playing the game 100 times.
The netted value is $__________.
The expected value of playing a $1 game of blackjack is $0.04, find the netted value after playing the game 100 times.
The netted value is $__________.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
65
A box contains one each of $4, $8, $25, $90, and $100 bills. You reach in and withdraw one bill. What is the expected value?
A) $114
B) $45
C) $25
D) $20
E) $227
A) $114
B) $45
C) $25
D) $20
E) $227

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
66
In a TV game show, four prizes are hidden on a game board which contains 60 spaces. One prize is worth $1,500, two prizes are worth $750, and the other prize is worth $50. The remaining spaces contain no prizes. The game show host offers a sure prize of $50 not to play this game. Should the contestant choose the sure prize or play the game?
Answer play, doesn't matter, or don't play.
Answer play, doesn't matter, or don't play.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose that you roll two dice. You will be paid $20 if you roll a double. You will not receive anything for any other outcome. How much should you be willing to pay for the privilege of rolling the dice? Please round your answer to the nearest cent.
$__________
$__________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
68
Heights (in inches) obtained by a group of people in a random survey is reported in the table. What is the expected height (in inches)? Heights
Probability
55
0)007
60
0)024
65
0)112
70
0)357
75
0)357
80
0)112
85
0)024
90
0)007
A) 80 in.
B) 78.3 in.
C) 78 in.
D) 71.8 in.
E) 72.5 in.
Probability
55
0)007
60
0)024
65
0)112
70
0)357
75
0)357
80
0)112
85
0)024
90
0)007
A) 80 in.
B) 78.3 in.
C) 78 in.
D) 71.8 in.
E) 72.5 in.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
69
In a TV game show, four prizes are hidden on a game board which contains 80 spaces. One prize is worth $4,000, two prizes are worth $2,000, and the other prize is worth $100. The remaining spaces contain no prizes. The game show host offers a sure prize of $100 not to play this game. Should the contestant choose the sure prize or play the game?
A) doesn't matter
B) play
C) don't play
A) doesn't matter
B) play
C) don't play

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
70
What is the expectation for the $1 four-number bet on a U.S. roulette wheel? 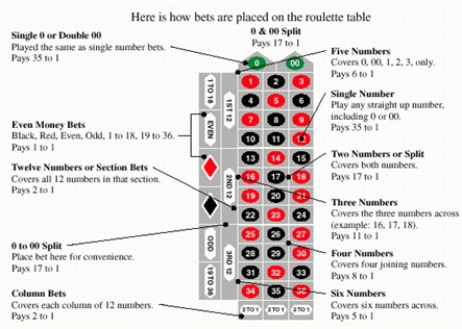
A) $0.05
B) $0.08
C) - $0.01
D) - $0.08
E) - $0.05

A) $0.05
B) $0.08
C) - $0.01
D) - $0.08
E) - $0.05

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
71
Consider a state lottery that has a weekly television show. On this show, a contestant receives the opportunity to win $1 million. The contestant picks from four hidden windows. Behind each is one of the following: $250,000, $125,000, $1 million, or a "stopper." Before beginning, the contestant is offered $300,000 to stop. Mathematically speaking, should the contestant take the $300,000?
Answer yes, no, or doesn't matter.
Answer yes, no, or doesn't matter.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
72
What is the expectation for the $1 black bet on a U.S. roulette wheel?
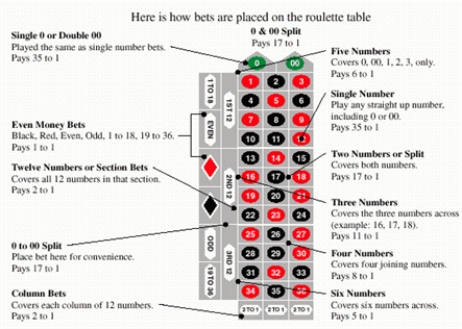
$__________

$__________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
73
Krinkles potato chips is having a "Lucky Seven Sweepstakes." The one grand prize is $70,000; 7 second prizes each pay $7,000; 77 third prizes each pay $700; and 777 fourth prizes each pay $70. What is the expectation of this contest, if there are 6 million entries? Please round your answer to the nearest cent.
$__________
$__________

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
74
What is the expectation for the $1 black bet on a U.S. roulette wheel? 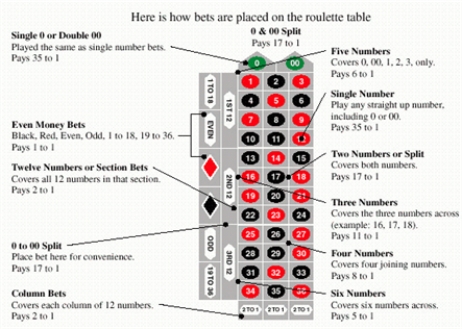
A) $0.05
B) - $0.01
C) $0.02
D) - $0.08
E) - $0.05

A) $0.05
B) - $0.01
C) $0.02
D) - $0.08
E) - $0.05

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
75
Krinkles potato chips is having a "Lucky Seven Sweepstakes." The one grand prize is $70,000; 7 second prizes each pay $7,000; 77 third prizes each pay $700; and 777 fourth prizes each pay $70. What is the expectation of this contest, if there are 9 million entries?
A) $0.05
B) $0.86
C) $0.03
D) $0.25
E) $0.01
A) $0.05
B) $0.86
C) $0.03
D) $0.25
E) $0.01

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
76
A single card is selected from an ordinary deck of cards. The sample space is shown in the figure below. Find the probability. 
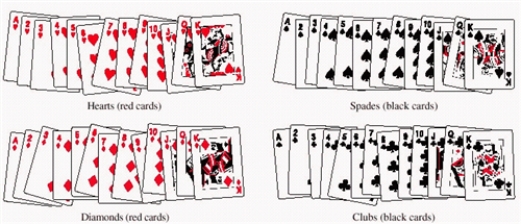
A)
B) 
C) 
D) 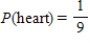
E) 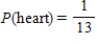
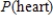

A)
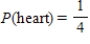
B)
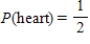
C)
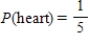
D)
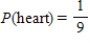
E)
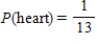

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
77
Consider a state lottery that has a weekly television show. On this show, a contestant receives the opportunity to win $1 million. The contestant picks from four hidden windows. Behind each is one of the following: $225,000, $300,000, $1 million, or a "stopper." Before beginning, the contestant is offered $400,000 to stop. Mathematically speaking, should the contestant take the $400,000?
A) yes
B) I don't know
C) doesn't matter
D) no
A) yes
B) I don't know
C) doesn't matter
D) no

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
78
Last year, 1,303 calculators were returned to the manufacturer. If 81,000 were produced, assign a number to specify the probability that a particular calculator would be returned.
A) about 0.016
B) about 0.130
C) about 0.033
D) about 0.058
E) about 0.012
A) about 0.016
B) about 0.130
C) about 0.033
D) about 0.058
E) about 0.012

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
79
An oil-drilling company knows that it costs $95,000 to sink a test well. If oil is hit, the income for the drilling company will be $875,000. If only natural gas is hit, the income will be $340,648. If nothing is hit, there will be no income. If the probability of hitting oil is 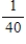 and if the probability of hitting gas is
and if the probability of hitting gas is 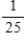 , what is the expectation for the drilling company? Should the company sink the test well? Please round your answer to the nearest dollar.
, what is the expectation for the drilling company? Should the company sink the test well? Please round your answer to the nearest dollar.
The expectation is __________, the company __________ (should, shouldn't) dig.
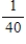 and if the probability of hitting gas is
and if the probability of hitting gas is 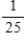 , what is the expectation for the drilling company? Should the company sink the test well? Please round your answer to the nearest dollar.
, what is the expectation for the drilling company? Should the company sink the test well? Please round your answer to the nearest dollar.
The expectation is __________, the company __________ (should, shouldn't) dig.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
80
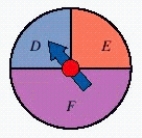
For the spinners assume that the pointer can never lie on a border line. Find 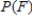 .
. 
A)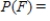

B) 

C) 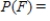

D) 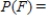

E) 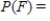

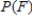 .
. 
A)
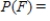

B)
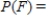

C)
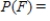

D)
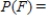

E)
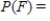


Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck


