Deck 8: The Nature of Measurement
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 8: The Nature of Measurement
1
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent.
A. a glass
B. a bowling ball
C. a sheet of typing paper
D. a ruler
E. a sphere
A) A, B, C, D and E
B) A, B, C, and E; D
C) A, B, C, and D; E
D) A; B, C, D and E
E) A, C and E; B; D
A. a glass
B. a bowling ball
C. a sheet of typing paper
D. a ruler
E. a sphere
A) A, B, C, D and E
B) A, B, C, and E; D
C) A, B, C, and D; E
D) A; B, C, D and E
E) A, C and E; B; D
A, B, C, D and E
2
Let X be a point obviously outside the figure. Draw 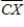 . How many times does it cross the curve?
. How many times does it cross the curve? 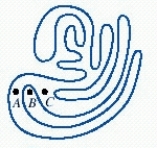
A) it will cross the curve an odd number of times
B) it will cross the curve an even number of times
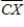 . How many times does it cross the curve?
. How many times does it cross the curve? 
A) it will cross the curve an odd number of times
B) it will cross the curve an even number of times
it will cross the curve an odd number of times
3
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent. 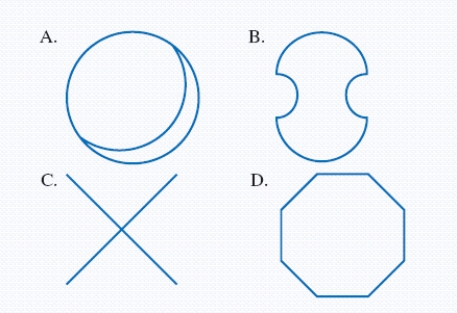

A; B AND D; C
4
Group the figures into classes so that all the elements within each class are topologically equivalent, and no elements from different classes are topologically equivalent. 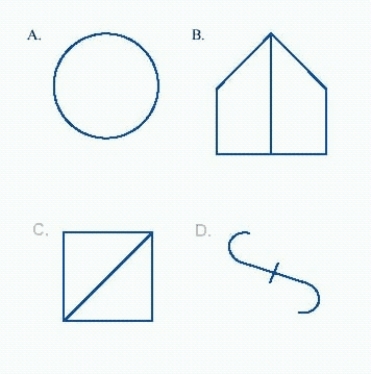
A) A; B and C; D
B) A and C; B; D
C) A and B; C; D
D) A and D; B; C
E) B and C; B; D

A) A; B and C; D
B) A and C; B; D
C) A and B; C; D
D) A and D; B; C
E) B and C; B; D

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Let X be a point obviously outside the figure. Draw 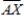 . How many times does it cross the curve?
. How many times does it cross the curve?
It will cross the curve an __________ (even, odd) number of times.
 . How many times does it cross the curve?
. How many times does it cross the curve?

It will cross the curve an __________ (even, odd) number of times.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
Group the figures into classes so that all the elements within each class are topologically equivalent, and no elements from different classes are topologically equivalent. 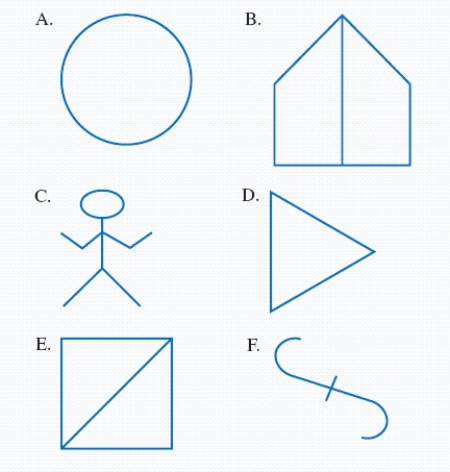


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent.
A. a bolt
B. a brick
C. a horseshoe
D. a pencil
A) A; B, C and D
B) A, C and D; B
C) A, B, and D
D) A, B, C, and D
E) A, B and C; D
A. a bolt
B. a brick
C. a horseshoe
D. a pencil
A) A; B, C and D
B) A, C and D; B
C) A, B, and D
D) A, B, C, and D
E) A, B and C; D

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
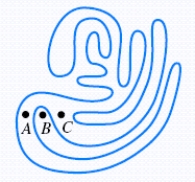
Determine whether each of the points A, B, and C is inside or outside of the simple closed curve.
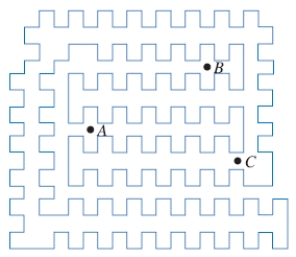 1. Point C
1. Point C
2. Point A
3. Point B
a. outside
b. inside
C
 1. Point C
1. Point C2. Point A
3. Point B
a. outside
b. inside
C

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent.
A) a bolt
B) a straw
C) a sewing needle
D) a funnel with a handle
A) a bolt
B) a straw
C) a sewing needle
D) a funnel with a handle

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent.
A) a glass
B) a bowling ball
C) a sheet of typing paper
D) a sheet of two-ring-binder paper
E) a sphere
A) a glass
B) a bowling ball
C) a sheet of typing paper
D) a sheet of two-ring-binder paper
E) a sphere

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
Let X be a point obviously outside the figure. Draw 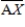 . How many times does it cross the curve?
. How many times does it cross the curve? 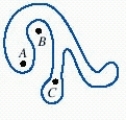
A) it will cross the curve an odd number of times
B) it will cross the curve an even number of times
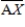 . How many times does it cross the curve?
. How many times does it cross the curve? 
A) it will cross the curve an odd number of times
B) it will cross the curve an even number of times

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
Let X be a point obviously outside the figure. Draw 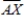 . How many times does it cross the curve?
. How many times does it cross the curve?
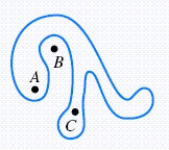
It will cross the curve an __________ (even, odd) number of times.
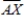 . How many times does it cross the curve?
. How many times does it cross the curve?

It will cross the curve an __________ (even, odd) number of times.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
Read the poem in the News Clip.  Is a right-handed mitten topologically equivalent to a left-handed mitten? Answer yes or no.
Is a right-handed mitten topologically equivalent to a left-handed mitten? Answer yes or no.
If a right-handed mitten is turned inside out, as is suggested in the poem, will it still fit a right hand? Answer yes or no.
 Is a right-handed mitten topologically equivalent to a left-handed mitten? Answer yes or no.
Is a right-handed mitten topologically equivalent to a left-handed mitten? Answer yes or no.If a right-handed mitten is turned inside out, as is suggested in the poem, will it still fit a right hand? Answer yes or no.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether the graph is a tree. 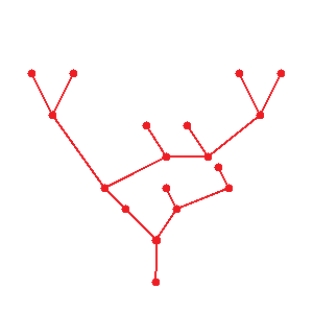
A) tree
B) not a tree

A) tree
B) not a tree

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
Read the poem in the News Clip.  a. If a right-handed mitten is turned inside out, as is suggested in the poem, will it still fit a right hand? b. Is a right-handed mitten topologically equivalent to a left-handed mitten?
a. If a right-handed mitten is turned inside out, as is suggested in the poem, will it still fit a right hand? b. Is a right-handed mitten topologically equivalent to a left-handed mitten?
A) a. no, b. yes
B) a. no, b. no
C) a. yes, b. no
D) a. yes, b. yes
 a. If a right-handed mitten is turned inside out, as is suggested in the poem, will it still fit a right hand? b. Is a right-handed mitten topologically equivalent to a left-handed mitten?
a. If a right-handed mitten is turned inside out, as is suggested in the poem, will it still fit a right hand? b. Is a right-handed mitten topologically equivalent to a left-handed mitten?A) a. no, b. yes
B) a. no, b. no
C) a. yes, b. no
D) a. yes, b. yes

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
Determine whether each of the points A, B, and C is inside or outside of the simple closed curve.
 1. Point C
1. Point C
2. Point A
3. Point B
a. outside
b. inside
A
 1. Point C
1. Point C2. Point A
3. Point B
a. outside
b. inside
A

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether each of the points A, B, and C is inside or outside of the simple closed curve.
 1. Point C
1. Point C
2. Point A
3. Point B
a. outside
b. inside
B
 1. Point C
1. Point C2. Point A
3. Point B
a. outside
b. inside
B

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent. 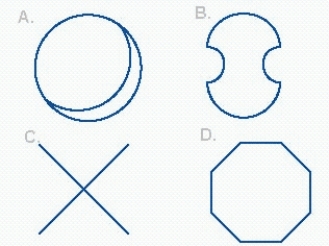
A) A, B and D; C
B) A; B and D; C
C) A; B, C and D
D) A,B,C, and D
E) A, C and D; B

A) A, B and D; C
B) A; B and D; C
C) A; B, C and D
D) A,B,C, and D
E) A, C and D; B

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
Is this figure tessellation? 
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether each of the points A, B, and C is inside or outside of the simple closed curve. 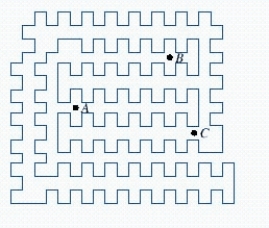
A) B and C are outside, A is inside
B) A and B are outside, C is inside
C) A and C are outside, B is inside
D) A is outside, B and C are inside
E) All are outside

A) B and C are outside, A is inside
B) A and B are outside, C is inside
C) A and C are outside, B is inside
D) A is outside, B and C are inside
E) All are outside

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
Find the minimum spanning tree for the of the graph. 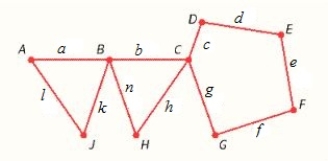
Where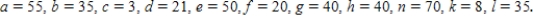
A) The sum of the numbers associated with the edges of the minimum spanning tree is 196
B) The sum of the numbers associated with the edges of the minimum spanning tree is 202
C) The sum of the numbers associated with the edges of the minimum spanning tree is 127
D) The sum of the numbers associated with the edges of the minimum spanning tree is 136
E) The sum of the numbers associated with the edges of the minimum spanning tree is 133

Where
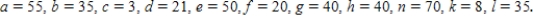
A) The sum of the numbers associated with the edges of the minimum spanning tree is 196
B) The sum of the numbers associated with the edges of the minimum spanning tree is 202
C) The sum of the numbers associated with the edges of the minimum spanning tree is 127
D) The sum of the numbers associated with the edges of the minimum spanning tree is 136
E) The sum of the numbers associated with the edges of the minimum spanning tree is 133

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
Use a tree to show the following family tree. You have two children, Shannon and Melissa. Shannon has two children, Soren and Thoren. Melissa has three children, Hannah, Banana, and Mike.
A)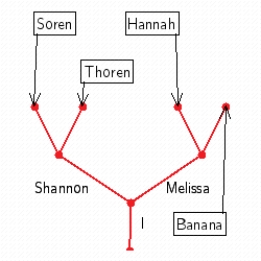
B)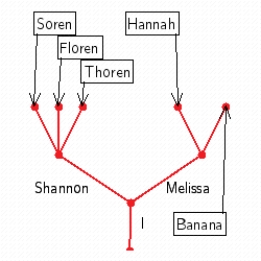
C)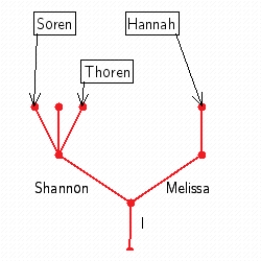
D)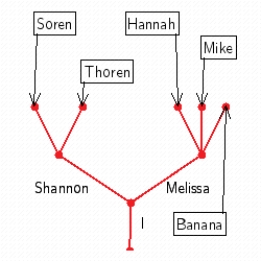
E)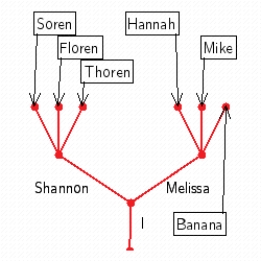
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
Is the network in c) an Euler circuit? Can this network can be traversed? 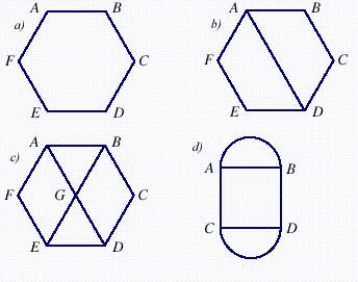
A) not an Euler circuit; traversable
B) not an Euler circuit; not traversable
C) an Euler circuit; traversable
D) an Euler circuit; not traversable

A) not an Euler circuit; traversable
B) not an Euler circuit; not traversable
C) an Euler circuit; traversable
D) an Euler circuit; not traversable

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose you wish to install a drip sprinkler system and need to run a drip water line to five areas, as shown in the given graph. The numbers show the distances in feet. What is the smallest number of feet of drip hose necessary to install?
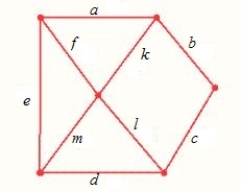
Where
__________ ft

Where
__________ ft

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
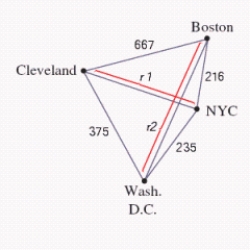
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington, D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if  ,
, 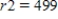 ? Find a solution using the brute-force method.
? Find a solution using the brute-force method. 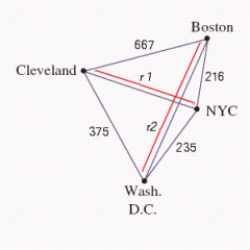
A) 1493 mi
B) 1495 mi
C) 1500 mi
D) 1487 mi
E) 2486 mi
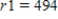 ,
, 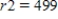 ? Find a solution using the brute-force method.
? Find a solution using the brute-force method. 
A) 1493 mi
B) 1495 mi
C) 1500 mi
D) 1487 mi
E) 2486 mi

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington,D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if 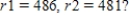 Find a solution using the nearest-neighbor method.
Find a solution using the nearest-neighbor method. 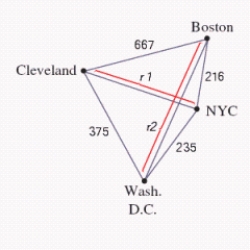
A) 1558 mi
B) 1,073 mi
C) 1,072 mi
D) 1,071 mi
E) 1,070 mi
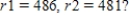 Find a solution using the nearest-neighbor method.
Find a solution using the nearest-neighbor method. 
A) 1558 mi
B) 1,073 mi
C) 1,072 mi
D) 1,071 mi
E) 1,070 mi

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
The map in figure shows driving distances and times between California and Nevada cities. Use Kruskal's algorithm to find the minimum spanning tree for the following cities: Santa Rosa, San Francisco, Oakland, Manteca, Yosemite Village, Merced, Fresno, and San Jose. 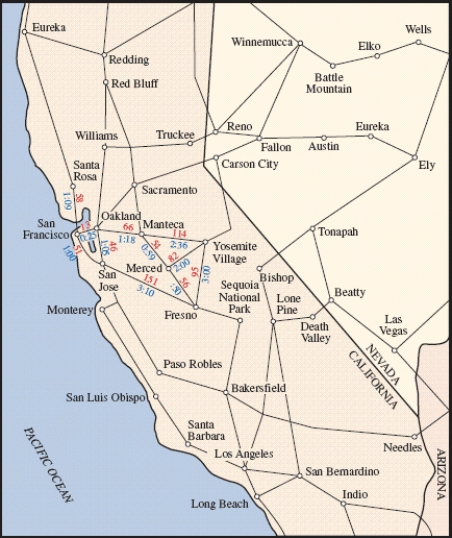 __________ mi
__________ mi
 __________ mi
__________ mi
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
Find two different spanning trees for the graph. 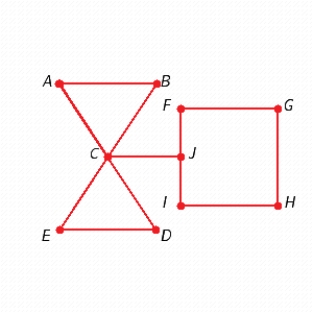
A)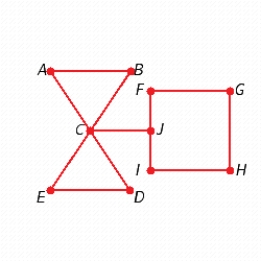
B)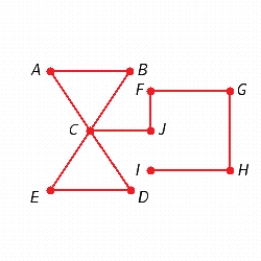
C)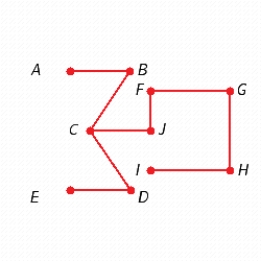
D)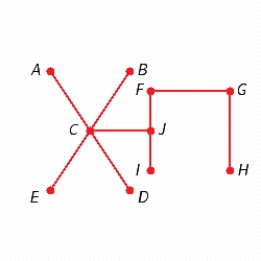
E)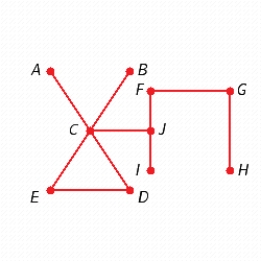

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington,D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if 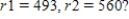 Find a solution using the sorted-edge method.
Find a solution using the sorted-edge method. 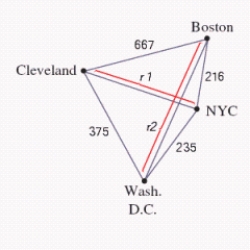
A) 1,646 mi
B) 1,645 mi
C) 1,151 mi
D) 1,643 mi
E) 1,644 mi
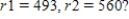 Find a solution using the sorted-edge method.
Find a solution using the sorted-edge method. 
A) 1,646 mi
B) 1,645 mi
C) 1,151 mi
D) 1,643 mi
E) 1,644 mi

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
Determine whether the graph is a tree or not a tree. 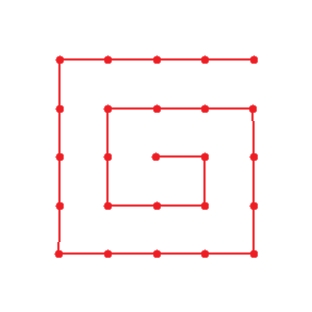


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
Can you pass the floor plan in b) through all the rooms while going through each door only once? 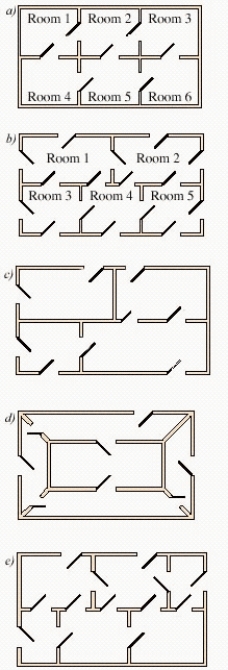
A) traversable
B) not traversable

A) traversable
B) not traversable

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
Draw graph for the molecule. Isobutane 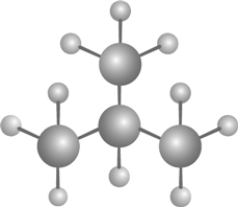
A)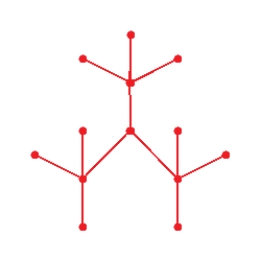
B)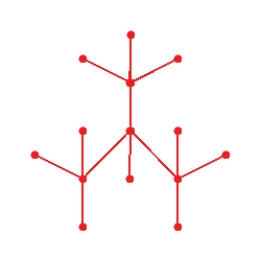
C)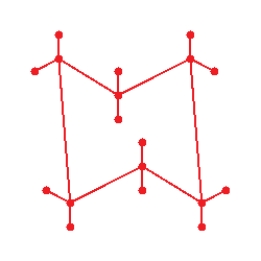
D)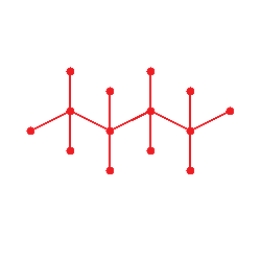
E)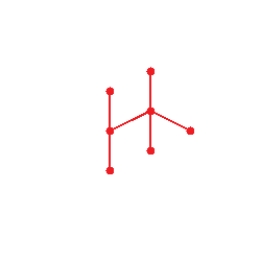

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
The map in figure shows driving distances and times between California and Nevada cities. Use Kruskal's algorithm to find the minimum spanning tree for the following cities: Santa Rosa, San Francisco, Oakland, Manteca, Yosemite Village, Merced, Fresno, and San Jose. 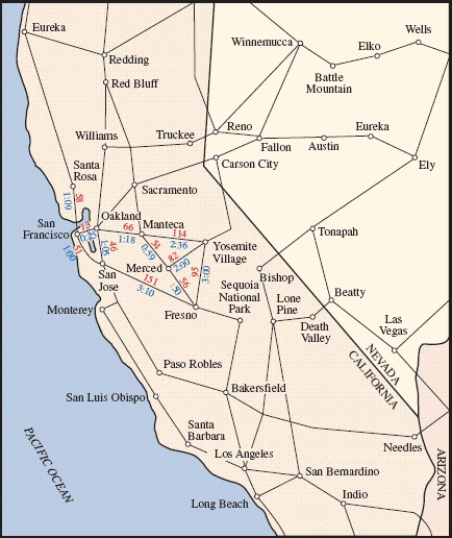
A) 426 mi
B) 211 mi
C) 370 mi
D) 786 mi
E) 375 mi

A) 426 mi
B) 211 mi
C) 370 mi
D) 786 mi
E) 375 mi

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
Does the network in a) have a Hamiltonian cycle? If this network has one, describe it. 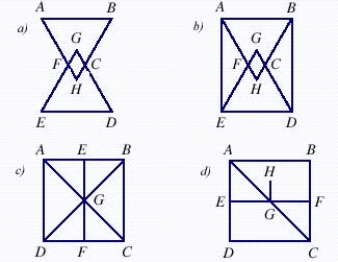
A) notpossible
B)
C)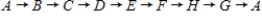
D)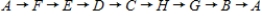
E)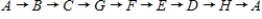

A) notpossible
B)
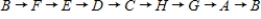
C)
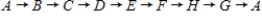
D)
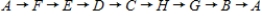
E)
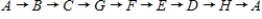

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
Draw graph for the molecule. Cyclopropane 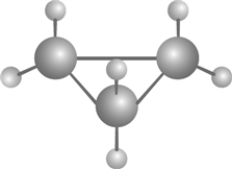
A)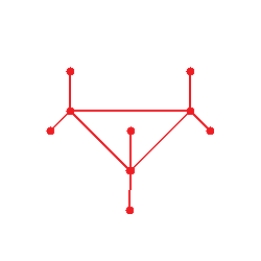
B)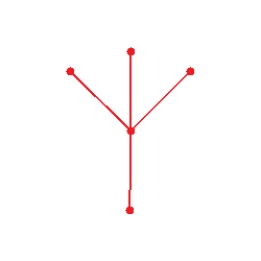
C)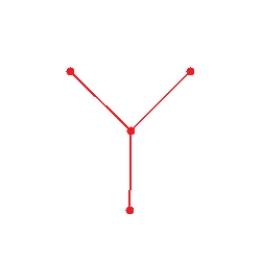
D)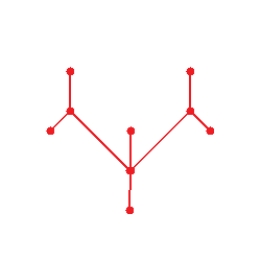
E)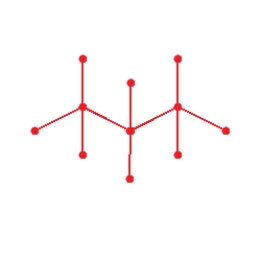

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
Is the network in d) an Euler circuit? Can this network can be traversed? 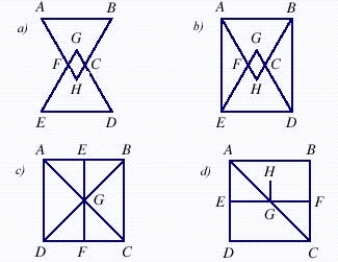
A) an Euler circuit; traversable
B) not an Euler circuit; traversable
C) not an Euler circuit; not traversable
D) an Euler circuit; not traversable

A) an Euler circuit; traversable
B) not an Euler circuit; traversable
C) not an Euler circuit; not traversable
D) an Euler circuit; not traversable

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
Find two different spanning trees for the graph. 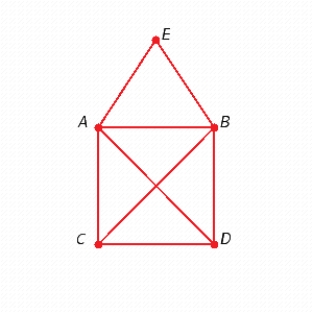
A)
B)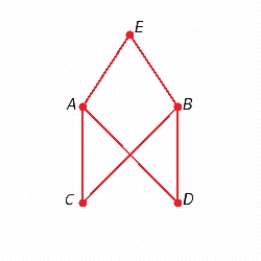
C)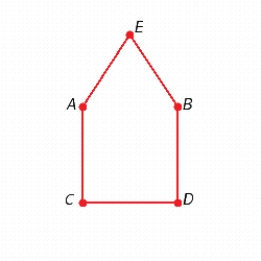
D)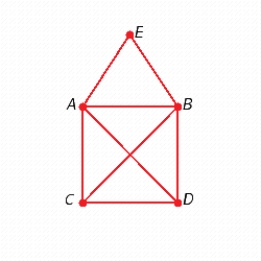
E)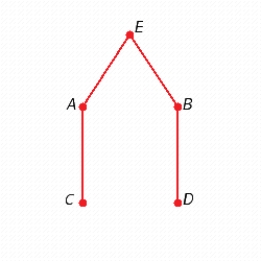

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose you wish to install a drip sprinkler system and need to run a drip water line to five areas, as shown in the given graph. The numbers show the distances in feet. What is the smallest number of feet of drip hose necessary to install? 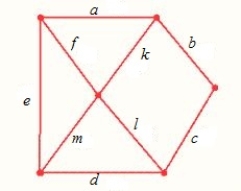
Where
A) The smallest number of feet of drip 214 ft
B) The smallest number of feet of drip 111 ft
C) The smallest number of feet of drip 126 ft
D) The smallest number of feet of drip 216 ft
E) The smallest number of feet of drip 153 ft

Where
A) The smallest number of feet of drip 214 ft
B) The smallest number of feet of drip 111 ft
C) The smallest number of feet of drip 126 ft
D) The smallest number of feet of drip 216 ft
E) The smallest number of feet of drip 153 ft

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
Does the network in d) have a Hamiltonian cycle? If this network has one, describe it. 
A)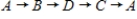
B)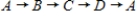
C)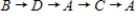
D)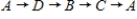
E) not possible

A)
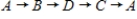
B)
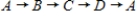
C)
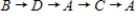
D)
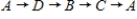
E) not possible

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
Find the minimum spanning tree for the of the graph.
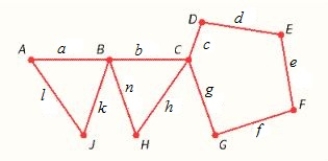
Where
The sum of the numbers associated with the edges of the minimum spanning tree is __________.

Where
The sum of the numbers associated with the edges of the minimum spanning tree is __________.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
On a planet far, far away, Luke finds himself in a strange building with hexagon-shaped rooms as shown in the figure below. In his search for the princess, he always moves to an adjacent room and always in a southerly direction. How many paths are there to room 1?
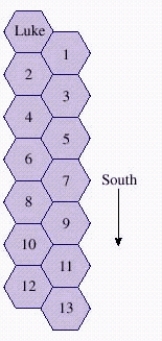
__________ path0

__________ path0

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Does the network in the picture below have Hamiltonian cycles? If the network has one, describe it. If not, answer not possible. 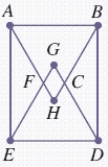


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Is the network a Euler circuit or a Hamiltonian circuit? 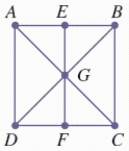 Can this network be traversed? Answer yes or no.
Can this network be traversed? Answer yes or no.
 Can this network be traversed? Answer yes or no.
Can this network be traversed? Answer yes or no.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
Is the network a Euler circuit or a Hamiltonian circuit?
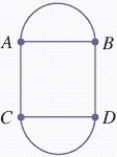
Can this network be traversed? Answer yes or no.

Can this network be traversed? Answer yes or no.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
Can you pass the floor plan in through all the rooms while going through each door only once? 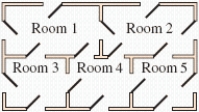 Answer traversable or not traversable.
Answer traversable or not traversable.
 Answer traversable or not traversable.
Answer traversable or not traversable.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
On a planet far, far away, Luke finds himself in a strange building with hexagon-shaped rooms as shown in the figure below. In his search for the princess, he always moves to an adjacent room and always in a southerly direction. How many paths are there to room 13? 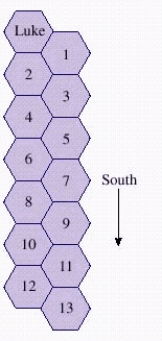
A) 381 paths
B) 378 paths
C) 375 paths
D) 377 paths
E) 256 paths

A) 381 paths
B) 378 paths
C) 375 paths
D) 377 paths
E) 256 paths

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington,
D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if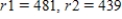 ? Find a solution using the brute-force method.
? Find a solution using the brute-force method.
__________ mi.
D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if
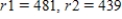 ? Find a solution using the brute-force method.
? Find a solution using the brute-force method.

__________ mi.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington,
D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if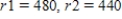 ? Find a solution using the nearest-neighbor method.
? Find a solution using the nearest-neighbor method.
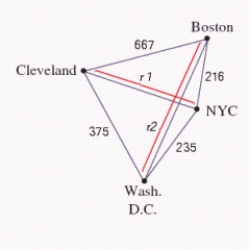
__________ mi.
D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if
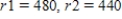 ? Find a solution using the nearest-neighbor method.
? Find a solution using the nearest-neighbor method.

__________ mi.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington,
D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if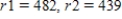 ? Find a solution using the sorted-edge method.
? Find a solution using the sorted-edge method.
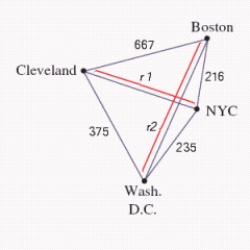
__________ mi.
D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if
 ? Find a solution using the sorted-edge method.
? Find a solution using the sorted-edge method.

__________ mi.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
Does the network in the picture below have a Hamiltonian cycle? If the network has one, describe it.


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck


