Deck 4: The Derivative in Graphing and Applications
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/656
Play
Full screen (f)
Deck 4: The Derivative in Graphing and Applications
1
Find the value for which f(x) = x2 + 2 on [2, 5] satisfies the Mean-Value Theorem.
A) 2.5
B) 3.5
C) 4.5
D) 3
E) 4
A) 2.5
B) 3.5
C) 4.5
D) 3
E) 4
3.5
2
Answer true or false. A graphing utility can be used to show that Rolle's Theorem can be applied to show that f(x) = (x - 8)2 has a point where f '(x) = 0.
False
3
Find the value c that satisfies Rolle's Theorem for f(x) = 9 cos 6x on 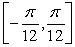 .
.
A)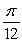
B)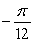
C) 0
D)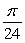
E)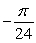
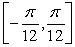 .
.A)
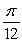
B)
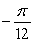
C) 0
D)
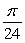
E)
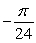
0
4
Answer true or false. According to Rolle's Theorem if a function's derivative is 0, the graph of the function must cross the y-axis.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
5
Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for ![Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for on [-2, 2].](https://storage.examlex.com/TB6988/11ead0bc_8ce6_dad1_99a0_e942af2f4c8f_TB6988_11.jpg) on [-2, 2].
on [-2, 2].
![Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for on [-2, 2].](https://storage.examlex.com/TB6988/11ead0bc_8ce6_dad1_99a0_e942af2f4c8f_TB6988_11.jpg) on [-2, 2].
on [-2, 2].
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
6
Answer true or false. ![Answer true or false. on [-3, 3] satisfies the hypotheses of Rolle's Theorem.](https://storage.examlex.com/TB6988/11ead0bc_8ce6_b3bf_99a0_3db7f5d470ee_TB6988_11.jpg) on [-3, 3] satisfies the hypotheses of Rolle's Theorem.
on [-3, 3] satisfies the hypotheses of Rolle's Theorem.
![Answer true or false. on [-3, 3] satisfies the hypotheses of Rolle's Theorem.](https://storage.examlex.com/TB6988/11ead0bc_8ce6_b3bf_99a0_3db7f5d470ee_TB6988_11.jpg) on [-3, 3] satisfies the hypotheses of Rolle's Theorem.
on [-3, 3] satisfies the hypotheses of Rolle's Theorem.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
7
Find the value c that satisfies the Mean-Value Theorem for f(x) = x3 on [0, 2].
A)![<strong>Find the value c that satisfies the Mean-Value Theorem for f(x) = x<sup>3</sup> on [0, 2].</strong> A) B) C) 2 D) 0 E)](https://storage.examlex.com/TB6988/11ead0bc_8ce7_7717_99a0_afb417a5e048_TB6988_11.jpg)
B)![<strong>Find the value c that satisfies the Mean-Value Theorem for f(x) = x<sup>3</sup> on [0, 2].</strong> A) B) C) 2 D) 0 E)](https://storage.examlex.com/TB6988/11ead0bc_8ce7_7718_99a0_992beda09f73_TB6988_11.jpg)
C) 2
D) 0
E)![<strong>Find the value c that satisfies the Mean-Value Theorem for f(x) = x<sup>3</sup> on [0, 2].</strong> A) B) C) 2 D) 0 E)](https://storage.examlex.com/TB6988/11ead0bc_8ce7_7719_99a0_071c3d9e8ecf_TB6988_11.jpg)
A)
![<strong>Find the value c that satisfies the Mean-Value Theorem for f(x) = x<sup>3</sup> on [0, 2].</strong> A) B) C) 2 D) 0 E)](https://storage.examlex.com/TB6988/11ead0bc_8ce7_7717_99a0_afb417a5e048_TB6988_11.jpg)
B)
![<strong>Find the value c that satisfies the Mean-Value Theorem for f(x) = x<sup>3</sup> on [0, 2].</strong> A) B) C) 2 D) 0 E)](https://storage.examlex.com/TB6988/11ead0bc_8ce7_7718_99a0_992beda09f73_TB6988_11.jpg)
C) 2
D) 0
E)
![<strong>Find the value c that satisfies the Mean-Value Theorem for f(x) = x<sup>3</sup> on [0, 2].</strong> A) B) C) 2 D) 0 E)](https://storage.examlex.com/TB6988/11ead0bc_8ce7_7719_99a0_071c3d9e8ecf_TB6988_11.jpg)

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
8
If ![<strong>If on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)</strong> A) 1.333 B) 1.540 C) 0.759 D) 1.923 E) 0.385](https://storage.examlex.com/TB6988/11ead0bc_8ce6_b3c0_99a0_f911d6efbd9e_TB6988_11.jpg) on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)
on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)
A) 1.333
B) 1.540
C) 0.759
D) 1.923
E) 0.385
![<strong>If on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)</strong> A) 1.333 B) 1.540 C) 0.759 D) 1.923 E) 0.385](https://storage.examlex.com/TB6988/11ead0bc_8ce6_b3c0_99a0_f911d6efbd9e_TB6988_11.jpg) on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)
on [0, 8], find the value c that satisfies the Mean-Value Theorem. (Round to three decimal places.)A) 1.333
B) 1.540
C) 0.759
D) 1.923
E) 0.385

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
9
Verify that f(x) = x3 -5x + 4 satisfies the hypothesis of the Mean-Value Theorem over the interval [-2, 3] and find all values of C that satisfy the conclusion of the theorem.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
10
Find the value c that satisfies Rolle's Theorem for f(x) = x3 -4x on [-2, 2].
A) -2.0
B) 1.2
C) 2.0
D) 4.0
E) -4.0
A) -2.0
B) 1.2
C) 2.0
D) 4.0
E) -4.0

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
11
Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for ![Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for on [0, 4 \pi ].](https://storage.examlex.com/TB6988/11ead0bc_8ce6_dad2_99a0_6143504b0922_TB6988_11.jpg) on [0, 4 ].
on [0, 4 ].
![Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for on [0, 4 \pi ].](https://storage.examlex.com/TB6988/11ead0bc_8ce6_dad2_99a0_6143504b0922_TB6988_11.jpg) on [0, 4 ].
on [0, 4 ]. 
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
12
Verify that f(x) = x2 + 7x - 3 satisfies the hypothesis of the Mean-Value Theorem over the interval [0, 1] and find all values of C that satisfy the conclusion of the theorem.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
13
Answer true or false. Rolle's Theorem is used to find the zeros of a function.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
14
Verify that f(x) = x3 - x satisfies the hypothesis of Rolle's Theorem on the interval [-1, 1] and find all values of C in (-1, 1) such that f '(C) = 0

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
15
Answer true or false. The hypotheses of the Mean-Value Theorem are satisfied for f(x) = cos 2x on [0, 4 ].

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
16
Find the value c such that the conclusion of Rolle's Theorem are satisfied for f(x) = 2x2 - 2 on [-3, 3].
A) 0
B) -1
C) 1
D) 0.5
E) -0.5
A) 0
B) -1
C) 1
D) 0.5
E) -0.5

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
17
Find the value for which f(x) = x3 -8 on [3, 7] satisfies the Mean-Value Theorem.
A) 4.509
B) 3.512
C) 8.888
D) 5.132
E) 6.285
A) 4.509
B) 3.512
C) 8.888
D) 5.132
E) 6.285

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
18
Answer true or false. The Mean-Value Theorem can be used on f(x) = |x - 3| on [-5, 5].

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
19
Answer true or false. The Mean-Value Theorem guarantees there is at least one c on [0, 1] such that f '(x) = 0.8 when f(x) = x.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
20
Find the value c that satisfies Rolle's Theorem for f(x) = cos 4x on 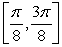 .
.
A)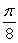
B) 4
C) 0
D)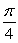
E)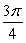
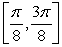 .
.A)
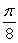
B) 4
C) 0
D)
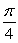
E)
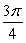

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
21
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [-3, 3]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_5d66_99a0_4117c727ba20_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [-3, 3]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [-3, 3]? If so, find all values of C that satisfy the conclusion of the theorem.
![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [-3, 3]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_5d66_99a0_4117c727ba20_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [-3, 3]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [-3, 3]? If so, find all values of C that satisfy the conclusion of the theorem.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
22
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.](https://storage.examlex.com/TB6988/11ead0bc_8cea_ab89_99a0_dd15e9331435_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.
![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.](https://storage.examlex.com/TB6988/11ead0bc_8cea_ab89_99a0_dd15e9331435_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 1]? If so, find all values of C that satisfy the conclusion.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
23
A cyclist starts from rest and travels 6.25 miles along a straight road in 15 minutes. Use the Mean-Value Theorem to show that at some instant during the trip his velocity was exactly 25 miles per hour.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
24
Use Rolle's Theorem to prove that the equation 6x5 - 28x3 + 6 = 0 has at least one solution in the interval (0, 1).

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
25
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_8478_99a0_55cf175bbf91_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.
![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_8478_99a0_55cf175bbf91_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 6]? If so, find all values of C that satisfy the conclusion of the theorem.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
26
Verify that f(x) = x2 + 8 satisfies the hypothesis of the Mean-Value Theorem on the interval [0, 4] and find all values of C that satisfy the conclusion of the theorem.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
27
Use Rolle's Theorem to show that f(x) = 4x3 + 5x - 1 does not have more than one real root.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
28
Find the value of c in the interval [0, 2 ] that satisfies the Mean Value Theorem. f(x) = 6 cos x

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
29
Use Rolle's Theorem to show that f(x) = x3 + ax + b, where a > 0, cannot have more than one real root.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
30
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [-5, 5]? If so, find all values of C that satisfy the conclusion.](https://storage.examlex.com/TB6988/11ead0bc_8ce8_8894_99a0_4fab22c15c77_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [-5, 5]? If so, find all values of C that satisfy the conclusion.
satisfy the hypothesis of the Mean-Value Theorem over the interval [-5, 5]? If so, find all values of C that satisfy the conclusion.
![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [-5, 5]? If so, find all values of C that satisfy the conclusion.](https://storage.examlex.com/TB6988/11ead0bc_8ce8_8894_99a0_4fab22c15c77_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [-5, 5]? If so, find all values of C that satisfy the conclusion.
satisfy the hypothesis of the Mean-Value Theorem over the interval [-5, 5]? If so, find all values of C that satisfy the conclusion.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
31
Find the value of c in the interval [0, 1] that satisfies the Mean Value Theorem. f(x) = x7

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
32
Verify that f(x) = x3 -3x2- 3x + 1 satisfies the hypothesis of the Mean-Value Theorem over the interval [0, 2] and find all values of C that satisfy the conclusion of the theorem.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
33
Find the value of c in the interval [0, 4] that satisfies the Mean Value Theorem. f(x) = 5x2 + 20

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
34
An automobile starts from rest and travels 4.5 miles along a straight road in 6 minutes. Use the Mean-Value Theorem to show that at some instant during the trip its velocity was exactly 45 miles per hour.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
35
Find the value of c in the interval [-1, 1] that satisfies the Mean Value Theorem. f(x) = x2 - 4x + 3

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
36
Verify that ![Verify that satisfies the hypothesis of the Mean-Value Theorem over the interval [6, 8] and find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8ce8_d6b6_99a0_254382027945_TB6988_11.jpg) satisfies the hypothesis of the Mean-Value Theorem over the interval [6, 8] and find all values of C that satisfy the conclusion of the theorem.
satisfies the hypothesis of the Mean-Value Theorem over the interval [6, 8] and find all values of C that satisfy the conclusion of the theorem.
![Verify that satisfies the hypothesis of the Mean-Value Theorem over the interval [6, 8] and find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8ce8_d6b6_99a0_254382027945_TB6988_11.jpg) satisfies the hypothesis of the Mean-Value Theorem over the interval [6, 8] and find all values of C that satisfy the conclusion of the theorem.
satisfies the hypothesis of the Mean-Value Theorem over the interval [6, 8] and find all values of C that satisfy the conclusion of the theorem.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
37
Approximate 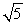 by applying Newton's Method to the equation x2 - 5 = 0. Use 2 for your initial value and calculate three iterations.
by applying Newton's Method to the equation x2 - 5 = 0. Use 2 for your initial value and calculate three iterations.
A) 2.2360680
B) 2.2359480
C) 2.2360560
D) 2.236111
E) 2.25
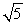 by applying Newton's Method to the equation x2 - 5 = 0. Use 2 for your initial value and calculate three iterations.
by applying Newton's Method to the equation x2 - 5 = 0. Use 2 for your initial value and calculate three iterations.A) 2.2360680
B) 2.2359480
C) 2.2360560
D) 2.236111
E) 2.25

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
38
Does ![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 16]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_0f41_99a0_f7b9f5c4837e_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 16]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 16]? If so, find all values of C that satisfy the conclusion of the theorem.
![Does satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 16]? If so, find all values of C that satisfy the conclusion of the theorem.](https://storage.examlex.com/TB6988/11ead0bc_8cea_0f41_99a0_f7b9f5c4837e_TB6988_11.jpg) satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 16]? If so, find all values of C that satisfy the conclusion of the theorem.
satisfy the hypothesis of the Mean-Value Theorem over the interval [0, 16]? If so, find all values of C that satisfy the conclusion of the theorem.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
39
Find the value of c in the interval [0, ] that satisfies the Mean Value Theorem. f(x) = sin(6x)

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
40
Find the value of c in the interval [0, 1] that satisfies the Mean Value Theorem. f(x) = x4 + 8

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
41
Use Newton's Method to find the largest positive solution of x4 + x3 - 2x2- 5x -7 = 0. Use 4 for your initial value and calculate eight iterations.
A) 3.0777385
B) 2.4705751
C) 2.0313608
D) 2.1446813
E) 2.0413802
A) 3.0777385
B) 2.4705751
C) 2.0313608
D) 2.1446813
E) 2.0413802

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
42
Use Newton's Method to find the x-coordinate of the intersection of y = x4 + 2x3 and y = 2x2 + 6x + 3. Use 3 for your initial value and calculate eight iterations.
A) 2.3333333
B) 1.9347826
C) 1.7649117
D) 1.7331057
E) 1.7320508
A) 2.3333333
B) 1.9347826
C) 1.7649117
D) 1.7331057
E) 1.7320508

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
43
Use Newton's Method to find the largest positive solution of x4 + 4x3 -2x2 - 9x - 2 = 0. Use 4 for your initial value and calculate eight iterations.
A) 1.6033441
B) 1.5530570
C) 1.8062561
D) 2.2423497
E) 2.9550827
A) 1.6033441
B) 1.5530570
C) 1.8062561
D) 2.2423497
E) 2.9550827

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
44
Use Newton's Method to approximate the greatest x-coordinate of the intersection of y = x3 - 2x and y = x4 + 6x - 4. Use 3 for your initial value and calculate eight iterations.
A) 0.5169625
B) 0.7963536
C) 0.5080644
D) 1.4400943
E) 2.1685393
A) 0.5169625
B) 0.7963536
C) 0.5080644
D) 1.4400943
E) 2.1685393

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
45
Approximate 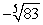 by applying Newton's Method to the equation x5 - 83 = 0. Use -2 for your initial value and calculate nine iterations.
by applying Newton's Method to the equation x5 - 83 = 0. Use -2 for your initial value and calculate nine iterations.
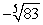 by applying Newton's Method to the equation x5 - 83 = 0. Use -2 for your initial value and calculate nine iterations.
by applying Newton's Method to the equation x5 - 83 = 0. Use -2 for your initial value and calculate nine iterations.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
46
Approximate 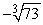 by applying Newton's Method to the equation x3 - 73 = 0. Use 4 for your initial value and calculate five iterations.
by applying Newton's Method to the equation x3 - 73 = 0. Use 4 for your initial value and calculate five iterations.
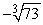 by applying Newton's Method to the equation x3 - 73 = 0. Use 4 for your initial value and calculate five iterations.
by applying Newton's Method to the equation x3 - 73 = 0. Use 4 for your initial value and calculate five iterations.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
47
Use Newton's Method to find the largest positive solution of x5 + 6x3-3x2 - 9 = 0. Use 3 for your initial value and calculate three iterations.
A) 2.3278689
B) 1.8122908
C) 1.4559632
D) 1.4558412
E) 1.4559512
A) 2.3278689
B) 1.8122908
C) 1.4559632
D) 1.4558412
E) 1.4559512

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
48
Use Newton's Method to find the largest positive solution of x4 + x3 - 6x - 6 = 0. Use 4 for your initial value and calculate eight iterations.
A) 1.8381538
B) 1.9835930
C) 1.8171206
D) 2.3659571
E) 3.0268456
A) 1.8381538
B) 1.9835930
C) 1.8171206
D) 2.3659571
E) 3.0268456

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
49
Approximate 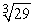 by applying Newton's Method to the equation x3 -29 = 0. Use 3 for your initial value and calculate five iterations.
by applying Newton's Method to the equation x3 -29 = 0. Use 3 for your initial value and calculate five iterations.
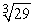 by applying Newton's Method to the equation x3 -29 = 0. Use 3 for your initial value and calculate five iterations.
by applying Newton's Method to the equation x3 -29 = 0. Use 3 for your initial value and calculate five iterations.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
50
Approximate 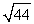 by applying Newton's Method to the equation x2 -44 = 0. Use 6 for your initial value and calculate five iterations.
by applying Newton's Method to the equation x2 -44 = 0. Use 6 for your initial value and calculate five iterations.
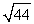 by applying Newton's Method to the equation x2 -44 = 0. Use 6 for your initial value and calculate five iterations.
by applying Newton's Method to the equation x2 -44 = 0. Use 6 for your initial value and calculate five iterations.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
51
Use Newton's Method to find the largest positive solution of x4 - 3x2 - 9 = 0. Use 5 for your initial value and calculate eight iterations.
A) 2.2697369
B) 2.5222928
C) 2.2032027
D) 3.0390141
E) 3.8489362
A) 2.2697369
B) 2.5222928
C) 2.2032027
D) 3.0390141
E) 3.8489362

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
52
Use Newton's Method to find the largest positive solution of x4 - 8x2 - 9 = 0. Use 4 for your initial value and calculate eight iterations.
A) 3.380208
B) 3.0000000
C) 3.0799923
D) 3.0045383
E) 3.0000157
A) 3.380208
B) 3.0000000
C) 3.0799923
D) 3.0045383
E) 3.0000157

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
53
Approximate 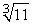 by applying Newton's Method to the equation x3 - 11 = 0. Use 2.5 for your initial value and calculate four iterations.
by applying Newton's Method to the equation x3 - 11 = 0. Use 2.5 for your initial value and calculate four iterations.
A) 2.5
B) 2.253333
C) 2.2243608
D) 2.2239800
E) 2.22398009
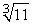 by applying Newton's Method to the equation x3 - 11 = 0. Use 2.5 for your initial value and calculate four iterations.
by applying Newton's Method to the equation x3 - 11 = 0. Use 2.5 for your initial value and calculate four iterations.A) 2.5
B) 2.253333
C) 2.2243608
D) 2.2239800
E) 2.22398009

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
54
The equation, x3 - 2x - 19 = 0 has one real solution for 1 < x < 19. Approximate it by Newton's Method. Use 4.75 for your initial value and calculate eight iterations.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
55
Use Newton's Method to find the largest solution of x5 - 2x4 + 5x3 -x2 + 7x + 12 = 0. Use 2 for your initial value and calculate six iterations.
A) 1.2151899
B) 0.0852538
C) -1.7308568
D) -1.0071278
E) -1.2897963
A) 1.2151899
B) 0.0852538
C) -1.7308568
D) -1.0071278
E) -1.2897963

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
56
Use Newton's Method to find the largest positive solution of x3 + x2 - 4x - 5 = 3. Use 4 for your initial value and calculate eight iterations.
A) 3.0769231
B) 2.5867842
C) 2.3921405
D) 2.3307530
E) 2.3417624
A) 3.0769231
B) 2.5867842
C) 2.3921405
D) 2.3307530
E) 2.3417624

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
57
Use Newton's Method to find the largest positive solution of x4 + 4x - 5 = 0. Use 4 for your initial value and calculate eight iterations.
A) 1.0000000
B) 1.2164332
C) 1.6112108
D) 2.1938904
E) 2.9730769
A) 1.0000000
B) 1.2164332
C) 1.6112108
D) 2.1938904
E) 2.9730769

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
58
Use Newton's Method to approximate the solutions of x4- 77 = 0. Use 4 for your initial value and calculate four iterations.
A) -3.0108653, 3.0108653
B) -2.9634212, 2.9634212
C) -2.9622573, 2.9622573
D) -3.300781, 3.300781
E) -4, 4
A) -3.0108653, 3.0108653
B) -2.9634212, 2.9634212
C) -2.9622573, 2.9622573
D) -3.300781, 3.300781
E) -4, 4

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
59
Use Newton's Method to find the greatest x-coordinate of the intersection of y = 4x4 -24x2 and y = 18x2 - 16. Use 9 for your initial value and calculate eight iterations.
A) 3.2978272
B) 3.1786982
C) 3.1888714
D) 4.3309497
E) 3.6519603
A) 3.2978272
B) 3.1786982
C) 3.1888714
D) 4.3309497
E) 3.6519603

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
60
Approximate 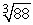 by applying Newton's Method to the equation x3 - 88 = 0. Use 4 for your initial value and calculate nine iterations.
by applying Newton's Method to the equation x3 - 88 = 0. Use 4 for your initial value and calculate nine iterations.
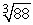 by applying Newton's Method to the equation x3 - 88 = 0. Use 4 for your initial value and calculate nine iterations.
by applying Newton's Method to the equation x3 - 88 = 0. Use 4 for your initial value and calculate nine iterations.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
61
Answer true or false. For the position function graphed, the acceleration at t = 1 is positive. 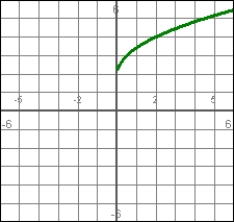


Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
62
The equation, x3 + x2 - 5x - 6 = 0 has one real solution for 1 < x < 6. Approximate it by Newton's Method. Use 3 for your initial value and calculate eight iterations.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
63
Let s(t) = t4 - 5t + 6 be a position function. The acceleration function a(t) =
A) 4t3 - 5
B) 12t2
C) 4t3 - 5t
D) 12t2 - 5
E) 12t3
A) 4t3 - 5
B) 12t2
C) 4t3 - 5t
D) 12t2 - 5
E) 12t3

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
64
Answer true or false. If a particle is dropped a distance of 624 m. It has a speed of 110.58 m/s (rounded to the nearest hundredth of a m/s) when it hits the ground.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
65
The graph represents a position function. Determine what is happening to the velocity at t = 0. 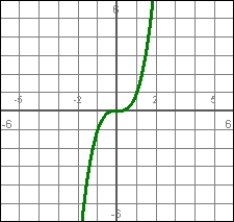
A) It is positive
B) It is negative
C) It is zero
D) There is insufficient information to tell.
E) It is +

A) It is positive
B) It is negative
C) It is zero
D) There is insufficient information to tell.
E) It is +

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
66
Let s(t) = t9 -t be a position function of a particle. At 1 the particle's acceleration is
A) negative
B) positive
C) zero
A) negative
B) positive
C) zero

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
67
The graph represents a position function. Determine what is happening to the velocity at t = 1. 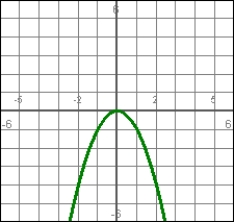
A) It is negative
B) It is positive
C) It is zero
D) There is insufficient information to tell.
E) It is +

A) It is negative
B) It is positive
C) It is zero
D) There is insufficient information to tell.
E) It is +

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
68
s(t) = 4t - 3t2, t 0. The velocity function is
A) 4 - 3t
B) 4t - 6t2
C) 4 - 6t
D) 8 - 6t
E) 4t - 3t
A) 4 - 3t
B) 4t - 6t2
C) 4 - 6t
D) 8 - 6t
E) 4t - 3t

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
69
A projectile is dropped, and reaches the ground at 40 m/s. How long does it take the projectile to reach ground? (Assume the position function is 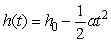 , where a = -10
, where a = -10 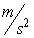 .)
.)
A) 2 s
B) 8 s
C) 4.47 s
D) 4 s
E) 3.16 s
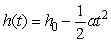 , where a = -10
, where a = -10 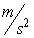 .)
.)A) 2 s
B) 8 s
C) 4.47 s
D) 4 s
E) 3.16 s

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
70
Let s(t) = sin 4t be a position function of a particle. At 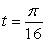 the particle's velocity is
the particle's velocity is
A) Positive
B) Negative
C) Zero
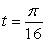 the particle's velocity is
the particle's velocity isA) Positive
B) Negative
C) Zero

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
71
The graph represents a velocity function. The acceleration at t = 2 is 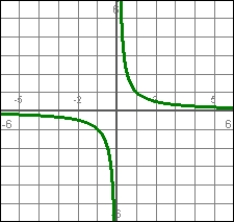
A) positive
B) negative
C) zero
D) There is insufficient information to tell.
E) It is +

A) positive
B) negative
C) zero
D) There is insufficient information to tell.
E) It is +

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
72
Find s when a = 0.
A) 48
B) -48
C) 6
D) -6
E) 0
A) 48
B) -48
C) 6
D) -6
E) 0

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
73
Answer true or false. This can be the graph of a particle's position if the particle is moving to the right at t = 3.3. 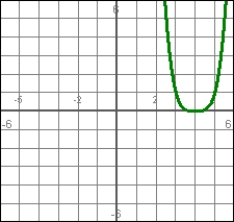


Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
74
Let s(t) = 5t6 -4t be a position function. Find v when t = 3.
A) 7,290
B) 1,455
C) 7,286
D) 3,633
E) 4
A) 7,290
B) 1,455
C) 7,286
D) 3,633
E) 4

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
75
The equation, 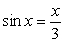 has one real solution for
has one real solution for 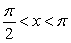 . Approximate it by Newton's Method. Use 2 for your initial value and calculate eight iterations.
. Approximate it by Newton's Method. Use 2 for your initial value and calculate eight iterations.
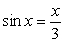 has one real solution for
has one real solution for 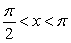 . Approximate it by Newton's Method. Use 2 for your initial value and calculate eight iterations.
. Approximate it by Newton's Method. Use 2 for your initial value and calculate eight iterations.
Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
76
s(t) = 5t-4t3, t 0. The acceleration function is
A) 5 - 8t
B) 8t
C) 5 - 8t2
D) 24t
E) 5t - 4t
A) 5 - 8t
B) 8t
C) 5 - 8t2
D) 24t
E) 5t - 4t

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
77
Answer true or false. If the graph on the left is a position function, the graph on the right represents the corresponding velocity function.
y = x2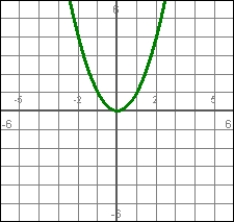
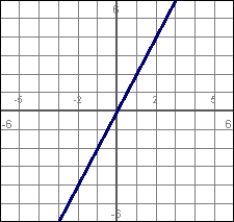
y = x2



Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
78
The equation, x3 - x2 - 4x - 4 = 0 has one real solution for 1 < x < 4. Approximate it by Newton's Method. Use 3 for your initial value and calculate eight iterations.

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
79
s(t) = 5t5- 11. Find t when a = 0.
A) 100
B) -100
C) 5
D) -5
E) 0
A) 100
B) -100
C) 5
D) -5
E) 0

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck
80
s(t) = t5 -10, t 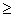 0. Find s when a = 0.
0. Find s when a = 0.
A) 20
B) -20
C) 10
D) -10
E) 0
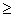 0. Find s when a = 0.
0. Find s when a = 0.A) 20
B) -20
C) 10
D) -10
E) 0

Unlock Deck
Unlock for access to all 656 flashcards in this deck.
Unlock Deck
k this deck


