Deck 13: Partial Derivatives
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/194
Play
Full screen (f)
Deck 13: Partial Derivatives
1
Use the Lagrange multiplier method to find the volume of the largest rectangular box that can be inscribed in the ellipsoid 2x2 + 3y2 + 4z2 = 12.
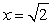 ,
, 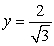 , and z = 1, thus, the maximum volume is
, and z = 1, thus, the maximum volume is 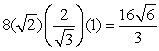 .
. 2
Use the Lagrange multiplier method to find the point on the plane x + 2y + 8z = 1 that is closest to the point (1, 1, 0).
The closest point to (1, 1, 0) is 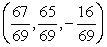 .
.
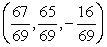 .
. 3
An open rectangular box is to contain 256 cubic inches. Use the Lagrange multiplier method to find the dimensions of the box which uses the least amount of material.
x = 8 in, y = 8 in, and z = 4 in.
4
Use Lagrange multipliers to find the volume of the largest rectangular box that can be inscribed within the sphere 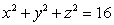 .
.
A)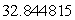
B)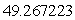
C)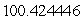
D)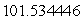
E)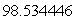
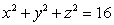 .
.A)
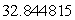
B)
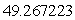
C)
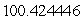
D)
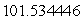
E)
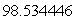

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
5
Use the Lagrange multiplier method to find three positive numbers whose sum is 16 and whose product, x2yz is a maximum.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
6
Let 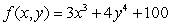 . There is a critical point at
. There is a critical point at
A) (10, 4)
B) (5, 2)
C) (-10, -4)
D) (0, 0)
E) (1, 1)
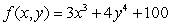 . There is a critical point at
. There is a critical point atA) (10, 4)
B) (5, 2)
C) (-10, -4)
D) (0, 0)
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
7
Use the Lagrange multiplier method to find the maximum sum of 2(x2 + y2 + z2) if
2(x + 2y + 2z) = 24.
2(x + 2y + 2z) = 24.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
8
An open rectangular box is to contain 864 cubic inches. Use the Lagrange multiplier method to find the dimensions of the box which uses the least amount of material.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
9
Use Lagrange multipliers to find all the locations of the extreme values of 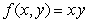 subject to
subject to 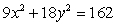 .
.
A) (0, 0)
B)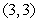 ,
,
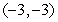
C)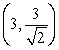 ,
,
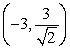
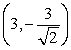 ,
,
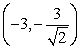
D)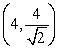 ,
,
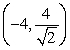
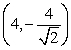 ,
,
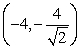
E) There are none
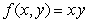 subject to
subject to 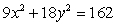 .
.A) (0, 0)
B)
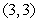 ,
,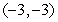
C)
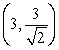 ,
,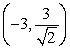
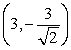 ,
,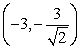
D)
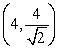 ,
,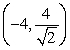
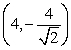 ,
,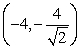
E) There are none

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
10
Use Lagrange multipliers to find all the locations of the extreme values of 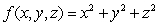 subject to
subject to 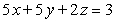 .
.
A) (0, 0, 0)
B)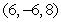
C)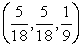
D)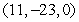
E) There are none
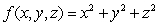 subject to
subject to 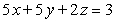 .
.A) (0, 0, 0)
B)
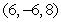
C)
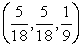
D)
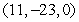
E) There are none

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
11
Use Lagrange multipliers to find the maximum and minimum values of 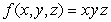 subject to
subject to 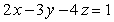 .
.
A) No maximum or minimum values.
B) The maximum value is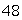 and the minimum value is
and the minimum value is
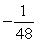
C) The maximum value is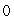 and the minimum value is
and the minimum value is
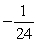
D) The maximum value is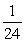 , and the minimum value is
, and the minimum value is
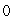
E) The maximum value is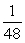 , and the minimum value is
, and the minimum value is
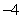
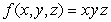 subject to
subject to 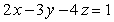 .
.A) No maximum or minimum values.
B) The maximum value is
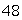 and the minimum value is
and the minimum value is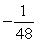
C) The maximum value is
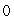 and the minimum value is
and the minimum value is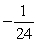
D) The maximum value is
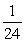 , and the minimum value is
, and the minimum value is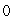
E) The maximum value is
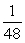 , and the minimum value is
, and the minimum value is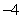

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
12
Use Lagrange multipliers to find maximum and minimum values of 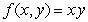 subject to
subject to 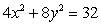 .
.
A) The maximum value is 0, and there is no minimum value. 2
B) The maximum value is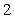 , and the minimum value is
, and the minimum value is
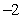
C) The maximum value is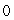 , and the minimum value is
, and the minimum value is
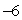
D) The maximum value is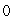 , and the minimum value is
, and the minimum value is
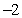
E) There is no maximum value, and the minimum value is 0.
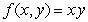 subject to
subject to 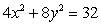 .
.A) The maximum value is 0, and there is no minimum value. 2
B) The maximum value is
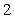 , and the minimum value is
, and the minimum value is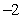
C) The maximum value is
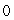 , and the minimum value is
, and the minimum value is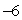
D) The maximum value is
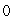 , and the minimum value is
, and the minimum value is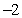
E) There is no maximum value, and the minimum value is 0.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
13
Use Lagrange multipliers to find all the locations of the extreme values of 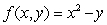 subject to
subject to 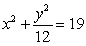 .
.
A) (0, 0)
B)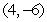
C)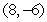 ,
,
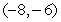
D)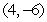 ,
,
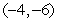
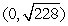 ,
,
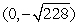
E) There are none
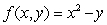 subject to
subject to 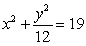 .
.A) (0, 0)
B)
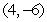
C)
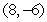 ,
,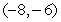
D)
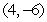 ,
,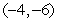
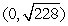 ,
,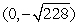
E) There are none

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
14
Use the Lagrange multiplier method to find the point on the surface z = xy + 10 that is closest to the origin.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
15
Use the Lagrange multiplier method to find three positive numbers whose sum is 12 and whose product, 2x2yz + 2 is a maximum.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
16
Use Lagrange multipliers to find all the locations of the extreme values of 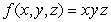 subject to
subject to 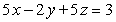 .
.
A) (0, 0, 0)
B)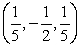
C)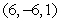
D)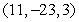
E) There are none
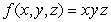 subject to
subject to 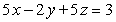 .
.A) (0, 0, 0)
B)
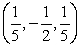
C)
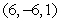
D)
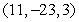
E) There are none

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
17
Use Lagrange multipliers to find the maximum and minimum values of 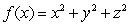 subject to
subject to 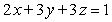 .
.
A) The maximum value is 0, and there is no minimum value.
B) The maximum value is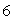 and the minimum value is
and the minimum value is
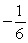
C) The minimum value is 0, and there is no maximum value.
D) The minimum value is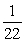 , and there is no maximum value.
, and there is no maximum value.
E) The maximum value is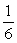 and the minimum value is 0.
and the minimum value is 0.
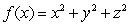 subject to
subject to 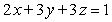 .
.A) The maximum value is 0, and there is no minimum value.
B) The maximum value is
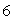 and the minimum value is
and the minimum value is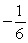
C) The minimum value is 0, and there is no maximum value.
D) The minimum value is
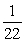 , and there is no maximum value.
, and there is no maximum value.E) The maximum value is
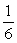 and the minimum value is 0.
and the minimum value is 0.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
18
Use Lagrange multipliers to find the volume of the largest rectangular box that can be inscribed within the ellipsoid 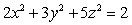 .
.
A)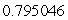
B)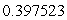
C)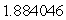
D)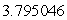
E)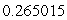
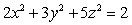 .
.A)
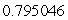
B)
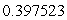
C)
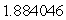
D)
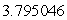
E)
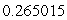

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
19
Use Lagrange multipliers to find the maximum and minimum values of 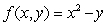 subject to
subject to 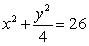 .
.
A) The maximum value is 0, and there is no minimum value.
B) The maximum value is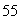 , and the minimum value is
, and the minimum value is
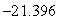
C) The maximum value is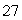 , and the minimum value is
, and the minimum value is
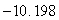
D) The maximum value is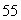 , and the minimum value is
, and the minimum value is
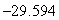
E) There is no maximum value, and the minimum value is 0.
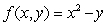 subject to
subject to 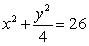 .
.A) The maximum value is 0, and there is no minimum value.
B) The maximum value is
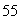 , and the minimum value is
, and the minimum value is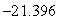
C) The maximum value is
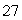 , and the minimum value is
, and the minimum value is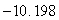
D) The maximum value is
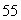 , and the minimum value is
, and the minimum value is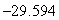
E) There is no maximum value, and the minimum value is 0.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
20
Let 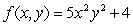 . There is a critical point at
. There is a critical point at
A) (10, 4)
B) (5, 2)
C) (-10, -4)
D) (0, 0)
E) (1, 1)
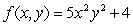 . There is a critical point at
. There is a critical point atA) (10, 4)
B) (5, 2)
C) (-10, -4)
D) (0, 0)
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
21
A rectangular box is to contain 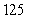 cubic inches. Find the dimensions of the box for which the surface area is a minimum.
cubic inches. Find the dimensions of the box for which the surface area is a minimum.
A)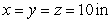
B)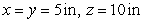
C)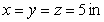
D)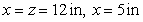
E)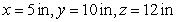
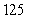 cubic inches. Find the dimensions of the box for which the surface area is a minimum.
cubic inches. Find the dimensions of the box for which the surface area is a minimum.A)
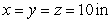
B)
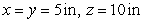
C)
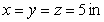
D)
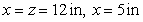
E)
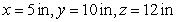

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
22
Find an equation for the tangent plane to 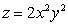 at
at 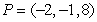 .
.
A)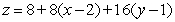
B)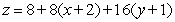
C)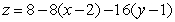
D)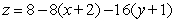
E)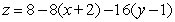
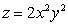 at
at 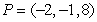 .
.A)
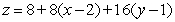
B)
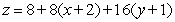
C)
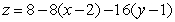
D)
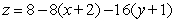
E)
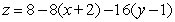

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
23
Find an equation for the tangent plane to 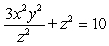 at
at 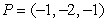 .
.
A)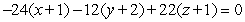
B)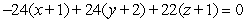
C)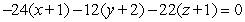
D)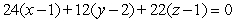
E)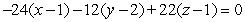
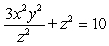 at
at 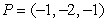 .
.A)
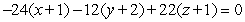
B)
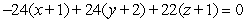
C)
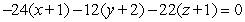
D)
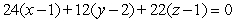
E)
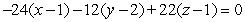

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
24
Find an equation for the tangent plane to 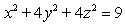 at
at 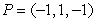 .
.
A)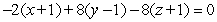
B)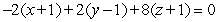
C)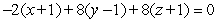
D)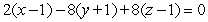
E)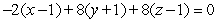
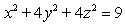 at
at 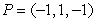 .
.A)
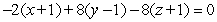
B)
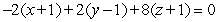
C)
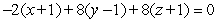
D)
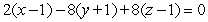
E)
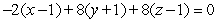

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
25
Let 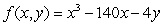 .
. 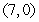 is
is
A) A relative maximum
B) A relative minimum
C) A saddle point
D) Cannot be determined
E) Both a relative maximum and a saddle point
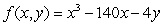 .
. 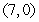 is
isA) A relative maximum
B) A relative minimum
C) A saddle point
D) Cannot be determined
E) Both a relative maximum and a saddle point

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
26
Let 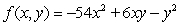 . There is a critical point at
. There is a critical point at
A) (0, 0)
B)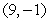
C)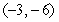
D) none exist
E) (1, 1)
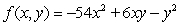 . There is a critical point at
. There is a critical point atA) (0, 0)
B)
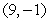
C)
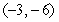
D) none exist
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
27
A rectangular box, open at the top, is to contain 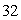 cubic inches. Find the dimensions of the box for which the surface area is a minimum.
cubic inches. Find the dimensions of the box for which the surface area is a minimum.
A)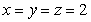 in
in
B)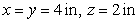
C)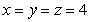
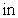
D)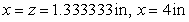
E)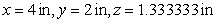
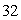 cubic inches. Find the dimensions of the box for which the surface area is a minimum.
cubic inches. Find the dimensions of the box for which the surface area is a minimum.A)
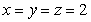 in
inB)
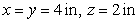
C)
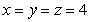
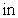
D)
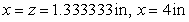
E)
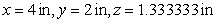

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
28
Locate all relative maxima, relative minima, and saddle points for
f(x, y) = x2 - xy + y 2 + 2x + 2y - 3.
f(x, y) = x2 - xy + y 2 + 2x + 2y - 3.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
29
Find an equation for the tangent plane to 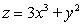 at
at 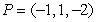 .
.
A)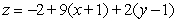
B)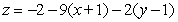
C)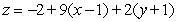
D)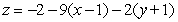
E)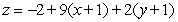
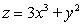 at
at 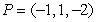 .
.A)
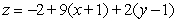
B)
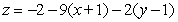
C)
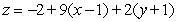
D)
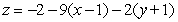
E)
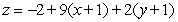

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
30
Find the point on 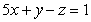 that is closest to the origin.
that is closest to the origin.
A)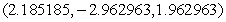
B)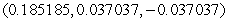
C)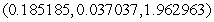
D)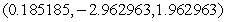
E)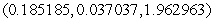
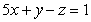 that is closest to the origin.
that is closest to the origin.A)
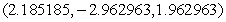
B)
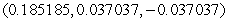
C)
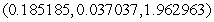
D)
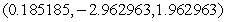
E)
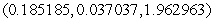

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
31
Let 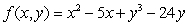 .
. 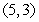 is
is
A) A relative maximum
B) A relative minimum
C) A saddle point
D) Cannot be determined
E) Both a relative maximum and a saddle point
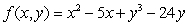 .
. 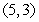 is
isA) A relative maximum
B) A relative minimum
C) A saddle point
D) Cannot be determined
E) Both a relative maximum and a saddle point

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
32
Let 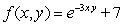 . There is a critical point at
. There is a critical point at
A) (0, 0)
B)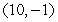
C)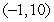
D) none exist
E) (1, 1)
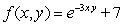 . There is a critical point at
. There is a critical point atA) (0, 0)
B)
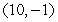
C)
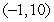
D) none exist
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
33
Find an equation for the tangent plane to 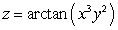 at
at 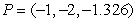 .
.
A)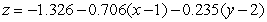
B)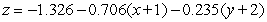
C)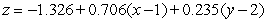
D)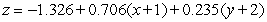
E)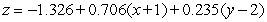
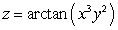 at
at 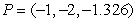 .
.A)
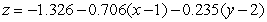
B)
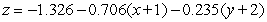
C)
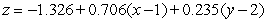
D)
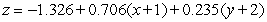
E)
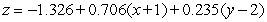

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
34
Let 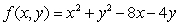 . There is a critical point at
. There is a critical point at
A) (10, 4)
B) (5, 2)
C)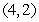
D) (0, 0)
E) (1, 1)
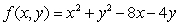 . There is a critical point at
. There is a critical point atA) (10, 4)
B) (5, 2)
C)
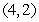
D) (0, 0)
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
35
Locate all relative maxima, relative minima, and saddle points for
f(x, y) = x2 - 2y2 - 6x + 8y + 41.
f(x, y) = x2 - 2y2 - 6x + 8y + 41.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
36
Let 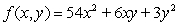 . There is a critical point at
. There is a critical point at
A) (0, 0)
B)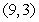
C)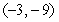
D) none exist
E) (1, 1)
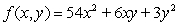 . There is a critical point at
. There is a critical point atA) (0, 0)
B)
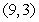
C)
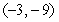
D) none exist
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
37
Find an equation for the tangent plane to 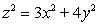 at
at 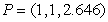 .
.
A)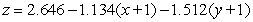
B)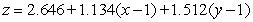
C)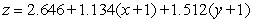
D)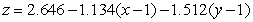
E)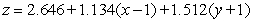
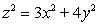 at
at 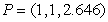 .
.A)
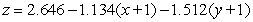
B)
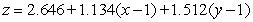
C)
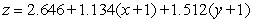
D)
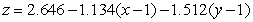
E)
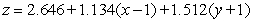

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
38
Find the minimum sum of 9x + 5y + 3z + 8 if x, y, and z are positive numbers such that xyz = 25.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
39
Find the point(s) on 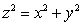 that are closest to
that are closest to 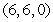 .
.
A)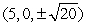
B)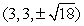
C)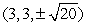 , and
, and
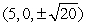
D) (0, 0, 0) and (1, 1, 1)
E)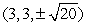
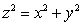 that are closest to
that are closest to 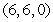 .
.A)
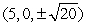
B)
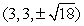
C)
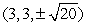 , and
, and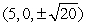
D) (0, 0, 0) and (1, 1, 1)
E)
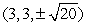

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
40
Let 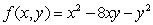 . There is a critical point at
. There is a critical point at
A) (0, 0)
B)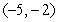
C)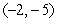
D) none exist
E) (1, 1)
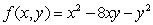 . There is a critical point at
. There is a critical point atA) (0, 0)
B)
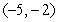
C)
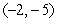
D) none exist
E) (1, 1)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
41
Find a point on the surface z = 16 - 12x2 - y2 at which the tangent plane is perpendicular to the line x = 3 + 12t, y = 2t, z = 2 - t.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
42
Find the equations of the tangent plane and normal line to z = xesin y at (2, , 5).Express the equation of the normal line parametrically.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
43
Let 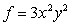 . Find
. Find 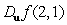 if
if 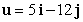 .
.
A)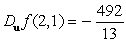
B)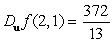
C)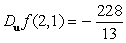
D)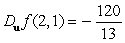
E)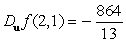
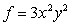 . Find
. Find 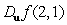 if
if 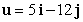 .
.A)
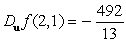
B)
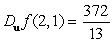
C)
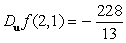
D)
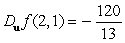
E)
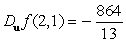

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
44
Let 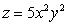 ; Find
; Find 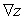 .
.
A)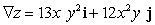
B)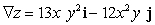
C)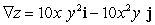
D)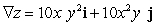
E)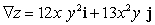
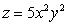 ; Find
; Find 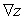 .
.A)
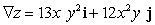
B)
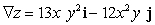
C)
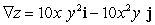
D)
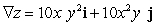
E)
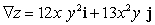

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
45
Let 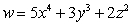 . Find
. Find 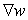 at the point
at the point 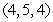 .
.
A)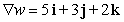
B)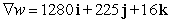
C)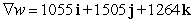
D)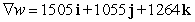
E)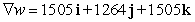
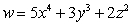 . Find
. Find 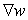 at the point
at the point 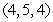 .
.A)
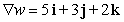
B)
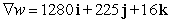
C)
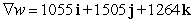
D)
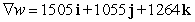
E)
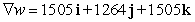

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
46
Find parametric equations for the normal line to 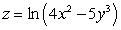 at
at 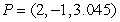 .
.
A)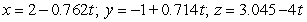
B)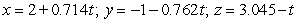
C)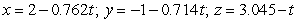
D)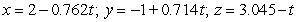
E)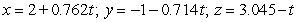
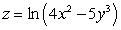 at
at 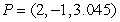 .
.A)
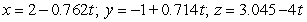
B)
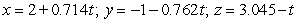
C)
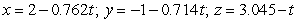
D)
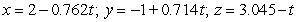
E)
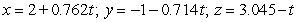

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
47
Find the equations of the tangent plane and normal line to 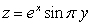 at
at 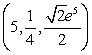 . Express the equation of the normal line parametrically.
. Express the equation of the normal line parametrically.
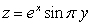 at
at 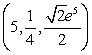 . Express the equation of the normal line parametrically.
. Express the equation of the normal line parametrically.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
48
Let 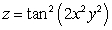 ; Find
; Find 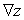 .
.
A)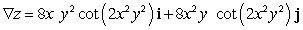
B)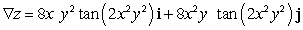
C)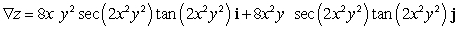
D)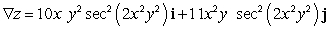
E)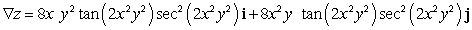
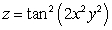 ; Find
; Find 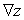 .
.A)
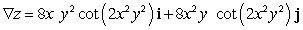
B)
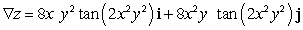
C)
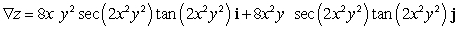
D)
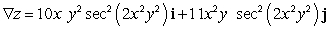
E)
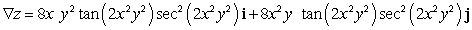

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
49
Let 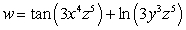 Find
Find 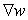 .
.
A)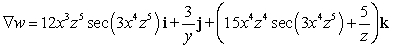
B)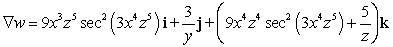
C)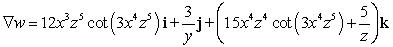
D)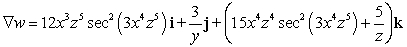
E)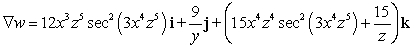
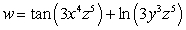 Find
Find 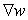 .
.A)
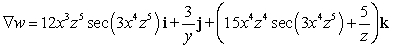
B)
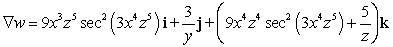
C)
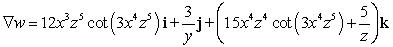
D)
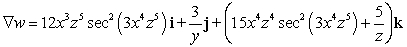
E)
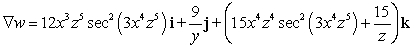

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
50
Let 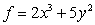 . Find
. Find 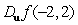 if
if 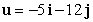 .
.
A)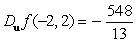
B)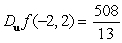
C)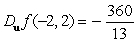
D)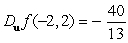
E)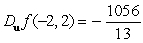
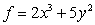 . Find
. Find 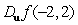 if
if 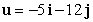 .
.A)
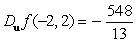
B)
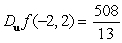
C)
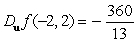
D)
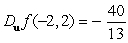
E)
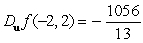

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
51
Find parametric equations for the normal line to 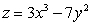 at
at 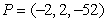 .
.
A)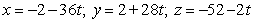
B)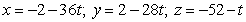
C)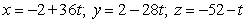
D)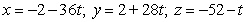
E)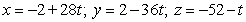
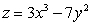 at
at 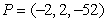 .
.A)
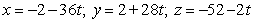
B)
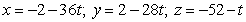
C)
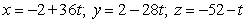
D)
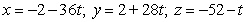
E)
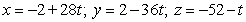

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
52
Find the equations of the tangent plane and normal line to 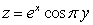 at
at 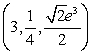 .Express the equation of the normal line parametrically.
.Express the equation of the normal line parametrically.
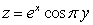 at
at 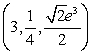 .Express the equation of the normal line parametrically.
.Express the equation of the normal line parametrically.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
53
Let 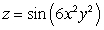 ; Find
; Find 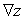 .
.
A)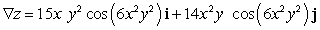
B)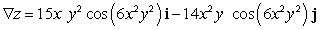
C)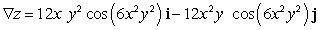
D)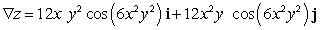
E)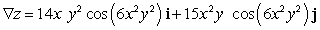
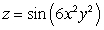 ; Find
; Find 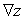 .
.A)
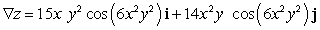
B)
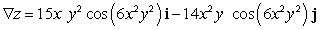
C)
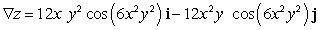
D)
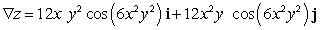
E)
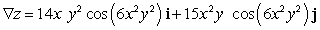

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
54
Find parametric equations for the normal line to 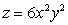 at
at 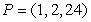 .
.
A)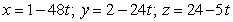
B)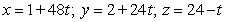
C)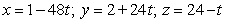
D)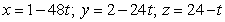
E)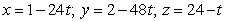
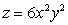 at
at 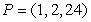 .
.A)
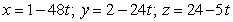
B)
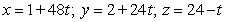
C)
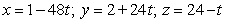
D)
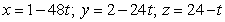
E)
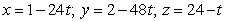

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
55
Find the equations of the tangent plane and normal line to x2z - xy2 - yz2 - 18 = 0 at (0, -2, 4).

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
56
Let 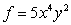 . Find
. Find 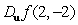 if
if 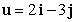 .
.
A)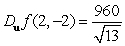
B)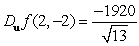
C)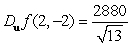
D)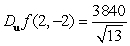
E)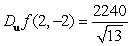
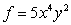 . Find
. Find 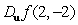 if
if 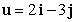 .
.A)
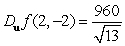
B)
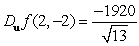
C)
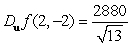
D)
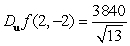
E)
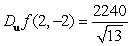

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
57
Let 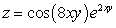 ; Find
; Find 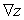 .
.
A)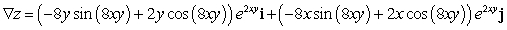
B)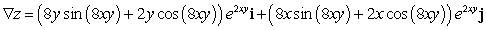
C)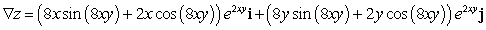
D)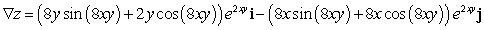
E)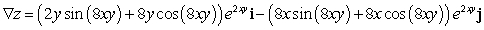
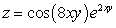 ; Find
; Find 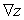 .
.A)
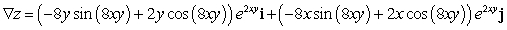
B)
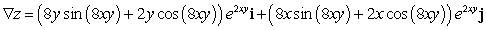
C)
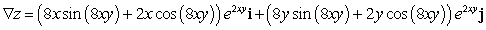
D)
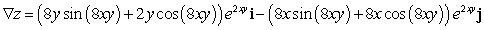
E)
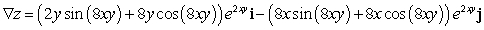

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
58
Find all points on the surface z = xe-y + 8 at which the tangent plane is horizontal.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
59
Let 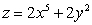 ; Find
; Find 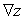 .
.
A)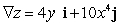
B)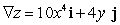
C)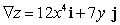
D)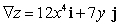
E)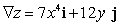
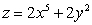 ; Find
; Find 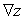 .
.A)
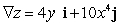
B)
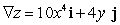
C)
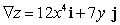
D)
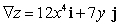
E)
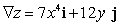

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
60
Let 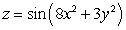 ; Find
; Find 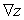 .
.
A)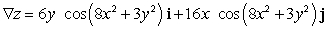
B)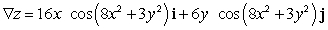
C)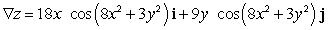
D)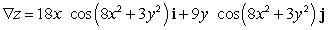
E)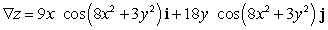
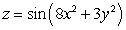 ; Find
; Find 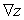 .
.A)
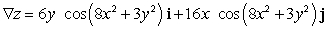
B)
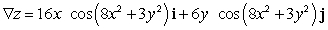
C)
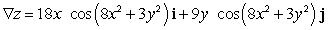
D)
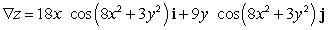
E)
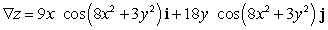

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
61
Find the rate of change of 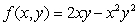 at
at 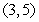 in the direction of
in the direction of 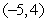 .
.
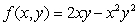 at
at 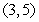 in the direction of
in the direction of 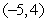 .
.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
62
Find the rate of change of 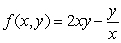 at (1, 6) in the direction of a vector making an angle of 120° with the positive x axis.
at (1, 6) in the direction of a vector making an angle of 120° with the positive x axis.
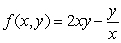 at (1, 6) in the direction of a vector making an angle of 120° with the positive x axis.
at (1, 6) in the direction of a vector making an angle of 120° with the positive x axis.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
63
A particle is located at the point (2, 7) on a metal surface whose temperature at a point (x, y) is T(x, y) = 16 - 2x2 - 3y2. Find the equation for the trajectory of a particle moving continuously in the direction of maximum temperature increase. y =
A)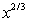
B)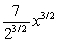
C)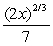
D)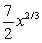
E) 1
A)
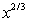
B)
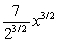
C)
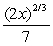
D)
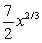
E) 1

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
64
Let 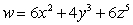 ;
; 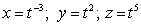 Find
Find 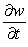 .
.
A)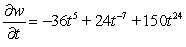
B)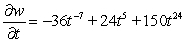
C)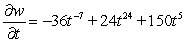
D)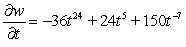
E)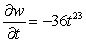
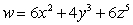 ;
; 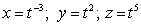 Find
Find 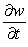 .
.A)
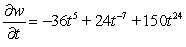
B)
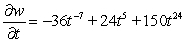
C)
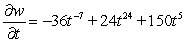
D)
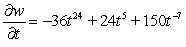
E)
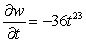

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
65
Find the gradient for f(x, y, z) = 7x4y3z.

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
66
Let 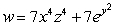 ;
; 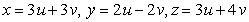 Find
Find 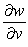 .
.
A)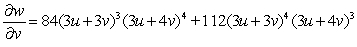
B)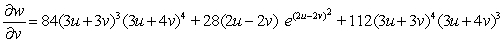
C)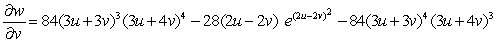
D)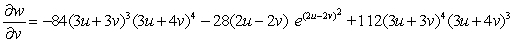
E)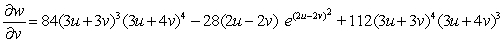
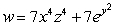 ;
; 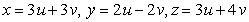 Find
Find 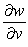 .
.A)
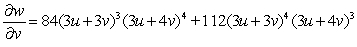
B)
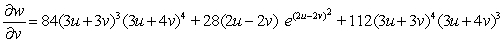
C)
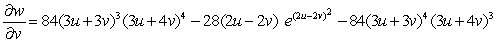
D)
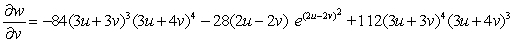
E)
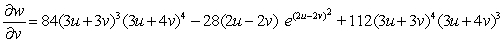

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
67
Let 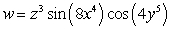 ;
; 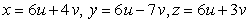 Find
Find 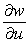 .
.
A)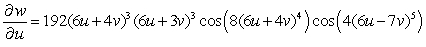
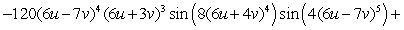
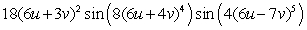
B)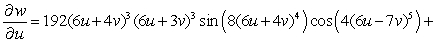
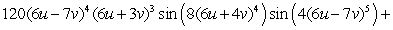
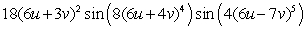
C)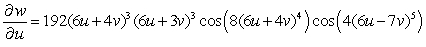
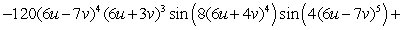
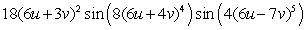
D)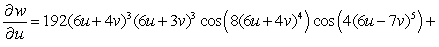
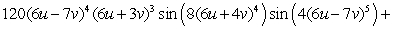
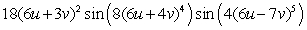
E)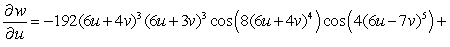
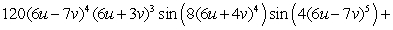
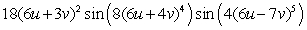
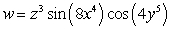 ;
; 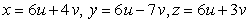 Find
Find 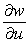 .
.A)
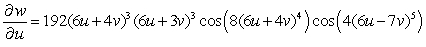
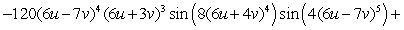
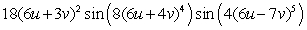
B)
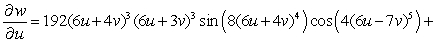
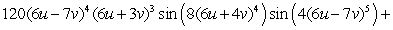
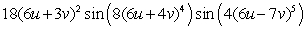
C)
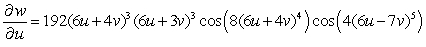
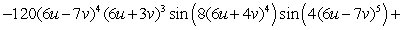
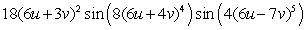
D)
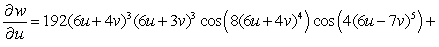
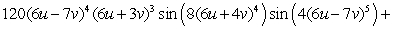
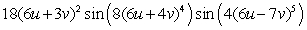
E)
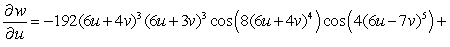
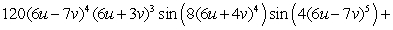
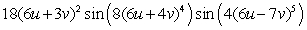

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
68
Let 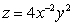 ; x = u + v , y = u - v. Find
; x = u + v , y = u - v. Find 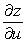 .
.
A)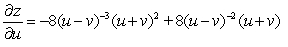
B)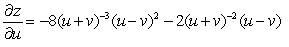
C)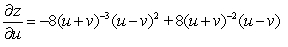
D)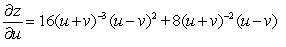
E)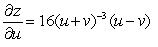
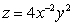 ; x = u + v , y = u - v. Find
; x = u + v , y = u - v. Find 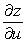 .
.A)
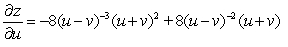
B)
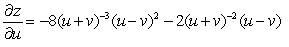
C)
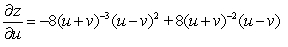
D)
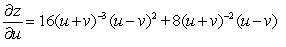
E)
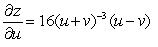

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
69
Let 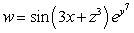 ; Find
; Find 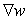 .
.
A)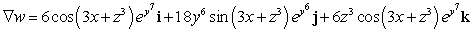
B)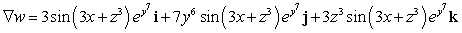
C)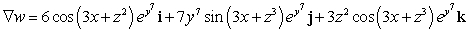
D)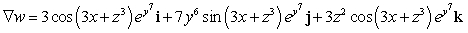
E)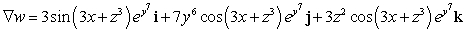
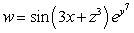 ; Find
; Find 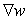 .
.A)
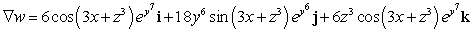
B)
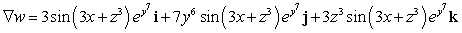
C)
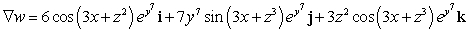
D)
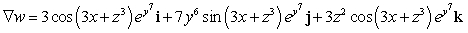
E)
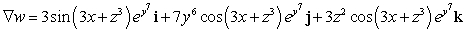

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
70
Let 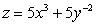 ;
; 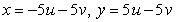 Find
Find 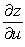 .
.
A)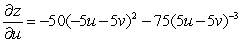
B)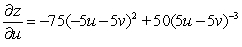
C)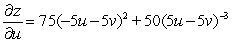
D)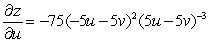
E)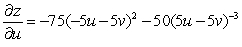
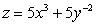 ;
; 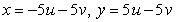 Find
Find 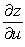 .
.A)
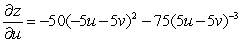
B)
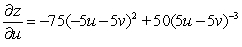
C)
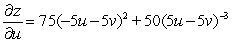
D)
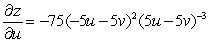
E)
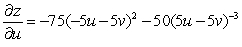

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
71
Let 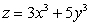 ;
; 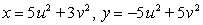 Find
Find 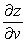 .
.
A)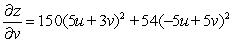
B)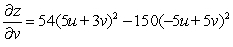
C)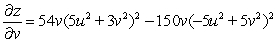
D)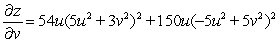
E)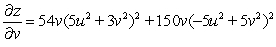
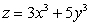 ;
; 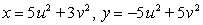 Find
Find 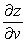 .
.A)
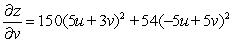
B)
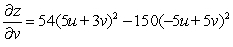
C)
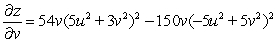
D)
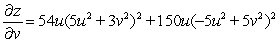
E)
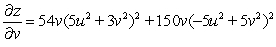

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
72
Let 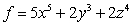 . Find
. Find 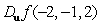 if
if 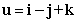 .
.
A)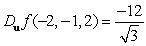
B)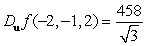
C)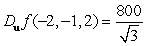
D)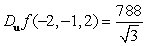
E)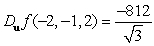
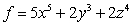 . Find
. Find 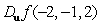 if
if 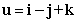 .
.A)
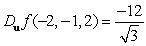
B)
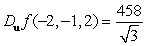
C)
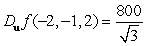
D)
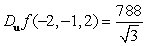
E)
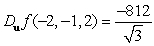

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
73
Let 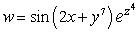 ;
; 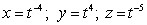 Find
Find 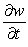 .
.
A)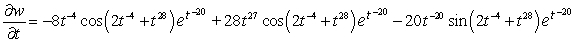
B)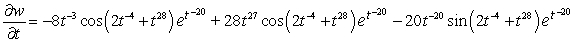
C)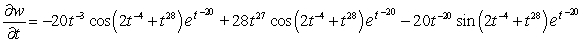
D)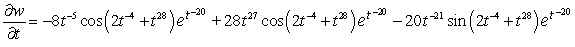
E)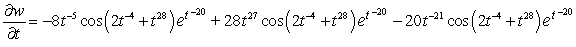
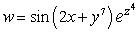 ;
; 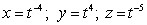 Find
Find 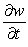 .
.A)
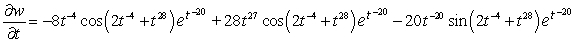
B)
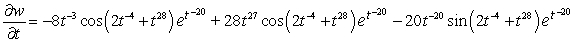
C)
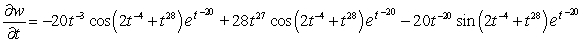
D)
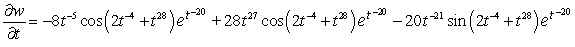
E)
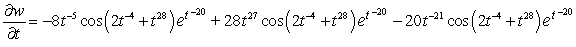

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
74
The sides of a rectangle are measured to be 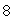 and
and 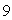 cm with a maximum error of
cm with a maximum error of 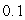 cm in each measurement. Use differentials to estimate the maximum possible error in the calculated value of the area.
cm in each measurement. Use differentials to estimate the maximum possible error in the calculated value of the area.
A)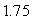 is the maximum error in the area.
is the maximum error in the area.
B) is the maximum error in the area.
is the maximum error in the area.
C)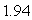 is the maximum error in the area.
is the maximum error in the area.
D)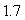 is the maximum error in the area.
is the maximum error in the area.
E)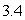 is the maximum error in the area.
is the maximum error in the area.
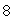 and
and 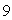 cm with a maximum error of
cm with a maximum error of 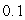 cm in each measurement. Use differentials to estimate the maximum possible error in the calculated value of the area.
cm in each measurement. Use differentials to estimate the maximum possible error in the calculated value of the area.A)
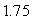 is the maximum error in the area.
is the maximum error in the area.B)
 is the maximum error in the area.
is the maximum error in the area.C)
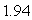 is the maximum error in the area.
is the maximum error in the area.D)
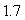 is the maximum error in the area.
is the maximum error in the area.E)
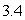 is the maximum error in the area.
is the maximum error in the area.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
75
Let 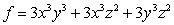 . Find
. Find 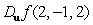 if
if 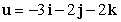 .
.
A)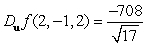
B)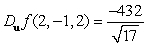
C)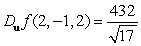
D)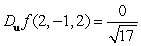
E)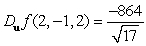
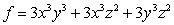 . Find
. Find 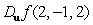 if
if 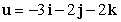 .
.A)
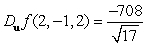
B)
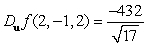
C)
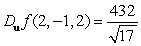
D)
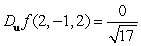
E)
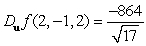

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
76
Let 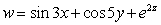 ;
; 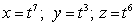 Find
Find 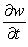 .
.
A)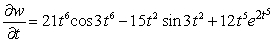
B)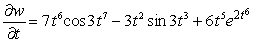
C)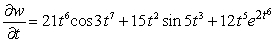
D)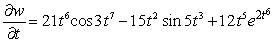
E)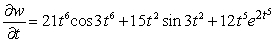
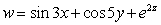 ;
; 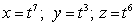 Find
Find 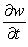 .
.A)
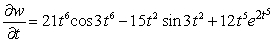
B)
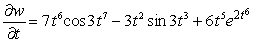
C)
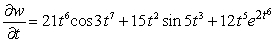
D)
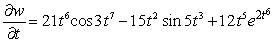
E)
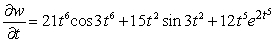

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
77
At t = 0, the position of a particle on a rectangular membrane is given by 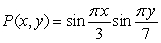 . Find the rate at which P changes if the particle moves from
. Find the rate at which P changes if the particle moves from 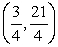 in a direction of a vector making an angle 30° with the positive x-axis.
in a direction of a vector making an angle 30° with the positive x-axis.
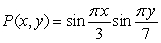 . Find the rate at which P changes if the particle moves from
. Find the rate at which P changes if the particle moves from 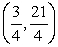 in a direction of a vector making an angle 30° with the positive x-axis.
in a direction of a vector making an angle 30° with the positive x-axis.
Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
78
A particle is located at the point (5, 5) on a metal surface whose temperature at a point (x, y) is T(x, y) = 25 - 3x2 - 2y2. Find the equation for the trajectory of a particle moving continuously in the direction of maximum temperature increase. y =
A)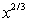
B)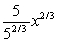
C)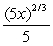
D)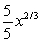
E) 1
A)
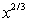
B)
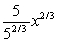
C)
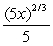
D)
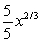
E) 1

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
79
Let 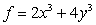 . Find
. Find 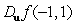 if
if 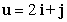 .
.
A)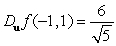
B)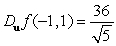
C)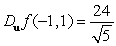
D)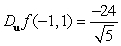
E)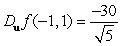
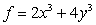 . Find
. Find 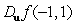 if
if 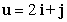 .
.A)
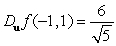
B)
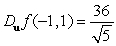
C)
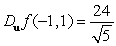
D)
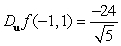
E)
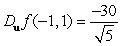

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck
80
Let 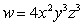 ;
; 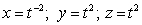 . Using the chain rule, find
. Using the chain rule, find 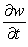 .
.
A)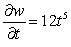
B)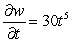
C)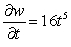
D)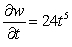
E)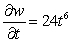
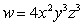 ;
; 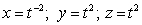 . Using the chain rule, find
. Using the chain rule, find 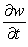 .
.A)
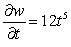
B)
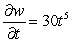
C)
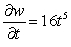
D)
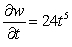
E)

Unlock Deck
Unlock for access to all 194 flashcards in this deck.
Unlock Deck
k this deck


