Deck 8: Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/111
Play
Full screen (f)
Deck 8: Sampling Distributions
1
If the sampled population is exactly normally distributed, then the sampling distribution of  is also expected to be normal, regardless of the sample size.
is also expected to be normal, regardless of the sample size.
 is also expected to be normal, regardless of the sample size.
is also expected to be normal, regardless of the sample size.True
2
As the sample size increases, the standard deviation of the sampling distribution increases.
False
3
The sampling distribution of the sample mean is developed by repeatedly taking samples of size n and computing the sample means and reporting the resulting sample means in the form of a probability distribution.
True
4
The standard deviation of the sampling distribution of the sample mean is σ.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
5
The Central Limit Theorem states that as sample size increases, the population distribution more closely approximates a normal distribution.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
6
A sample statistic is an unbiased point estimate of a population parameter if the mean of the populations of all possible values of the sample statistic equals the population parameter.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
7
The reason sample variance has a divisor of n − 1 rather than n is that it makes the variance an unbiased estimate of the population variance.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
8
If a population is known to be normally distributed, then the single sample mean must equal the population mean.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
9
For any sampled population, the population of all sample means is approximately normally distributed.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
10
A minimum-variance unbiased point estimate has a variance that is as small as or smaller than the variances of any other unbiased point estimate.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
11
If the sampled population distribution is skewed then, in most cases, the sampling distribution of the mean can be approximated by the normal distribution if the sample size, n, is at least 30.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
12
If a population is known to be normally distributed, then the sample standard deviation must equal σ.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
13
The mean of the sampling distribution of  is always equal to the mean of the sampled population.
is always equal to the mean of the sampled population.
 is always equal to the mean of the sampled population.
is always equal to the mean of the sampled population.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
14
The standard deviation of all possible sample proportions increases as the sample size increases.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
15
If p = .8 and n = 50, then we can conclude that the sampling distribution of  is approximately a normal distribution.
is approximately a normal distribution.
 is approximately a normal distribution.
is approximately a normal distribution.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
16
If p = .9 and n = 40, then we can conclude that the sampling distribution of  is approximately a normal distribution.
is approximately a normal distribution.
 is approximately a normal distribution.
is approximately a normal distribution.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
17
If we have a sample size of 100 and the estimate of the population proportion is .10, we can estimate the sampling distribution of  with a normal distribution.
with a normal distribution.
 with a normal distribution.
with a normal distribution.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
18
The sampling distribution of  must be a normal distribution with mean = 0 and standard deviation = 1.
must be a normal distribution with mean = 0 and standard deviation = 1.
 must be a normal distribution with mean = 0 and standard deviation = 1.
must be a normal distribution with mean = 0 and standard deviation = 1.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
19
A sample size of 500 is sufficiently large to conclude that the sampling distribution of  is a normal distribution, when the estimate of the population proportion is .995.
is a normal distribution, when the estimate of the population proportion is .995.
 is a normal distribution, when the estimate of the population proportion is .995.
is a normal distribution, when the estimate of the population proportion is .995.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
20
The sampling distribution of a sample statistic is the probability distribution of the population of all possible values of the sample statistic.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
21
The quantity 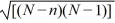 is called the finite population multiplier.
is called the finite population multiplier.
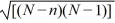 is called the finite population multiplier.
is called the finite population multiplier.
Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
22
The mean of the sampling distribution of the sample proportion is equal to ________ when the sample size is sufficiently large.
A) μ
B) p
C) p × n
D) (1 − p)
A) μ
B) p
C) p × n
D) (1 − p)

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
23
The population of all sample proportions has a normal distribution if the sample size (n) is sufficiently large. The rule of thumb for ensuring that n is sufficiently large is
A) np ≥ 5.
B) n(1 − p) ≥ 5.
C) np ≤ 5.
D) n(1 − p) ≤ 5 and np ≤ 5.
E) np ≥ 5 and n(1 − p) ≥ 5.
A) np ≥ 5.
B) n(1 − p) ≥ 5.
C) np ≤ 5.
D) n(1 − p) ≤ 5 and np ≤ 5.
E) np ≥ 5 and n(1 − p) ≥ 5.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
24
The notation for the standard deviation of the sampling distribution of the sample mean is ________.
A)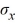 or
or
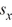
B) σx
C) σ
 /n
/n
D) μ
A)
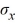 or
or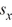
B) σx
C) σ
 /n
/nD) μ

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
25
________ says that if the sample size is sufficiently large, then the sample means are approximately normally distributed.
A) Cluster sampling
B) Sampling error
C) Sampling distribution of the mean
D) The Central Limit Theorem
A) Cluster sampling
B) Sampling error
C) Sampling distribution of the mean
D) The Central Limit Theorem

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
26
The sample standard deviation s is an unbiased estimator of the population standard deviation σ.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
27
If the sampled population has a mean of 48 and standard deviation of 16, then respectively the mean and the standard deviation for the sampling distribution of  for n = 16 are
for n = 16 are
A) 4 and 1.
B) 12 and 4.
C) 48 and 4.
D) 48 and 1.
E) 48 and 16.
 for n = 16 are
for n = 16 areA) 4 and 1.
B) 12 and 4.
C) 48 and 4.
D) 48 and 1.
E) 48 and 16.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
28
As the sample size ________, the variation of the sampling distribution of  ________.
________.
A) decreases, decreases
B) increases, remains the same
C) decreases, remains the same
D) increases, decreases
E) None of these answers is correct.
 ________.
________.A) decreases, decreases
B) increases, remains the same
C) decreases, remains the same
D) increases, decreases
E) None of these answers is correct.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
29
According to the Central Limit Theorem, if a sample size is at least ________, then for most sampled populations, we can conclude that the sample means are approximately normal.
A) 25
B) 20
C) 30
D) 50
A) 25
B) 20
C) 30
D) 50

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
30
If the sample size n is infinitely large, then s2 is an unbiased estimator of σ2.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
31
Consider a sampling distribution formed based on n = 3. The standard deviation of the population of all sample means 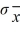 is ________ less than the standard deviation of the population of individual measurements σ.
is ________ less than the standard deviation of the population of individual measurements σ.
A) always
B) sometimes
C) never
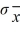 is ________ less than the standard deviation of the population of individual measurements σ.
is ________ less than the standard deviation of the population of individual measurements σ.A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
32
The Central Limit Theorem states that as the sample size increases, the distribution of the sample ________ approaches the normal distribution.
A) medians
B) means
C) standard deviations
D) variances
A) medians
B) means
C) standard deviations
D) variances

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
33
There is no easy way to calculate an unbiased point estimate of σ.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
34
The spread of the sampling distribution of  is ________ the spread of the corresponding population distribution sampling distribution.
is ________ the spread of the corresponding population distribution sampling distribution.
A) larger than
B) smaller than
C) the same as
D) exactly 1/2
 is ________ the spread of the corresponding population distribution sampling distribution.
is ________ the spread of the corresponding population distribution sampling distribution.A) larger than
B) smaller than
C) the same as
D) exactly 1/2

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
35
For nonnormal populations, as the sample size (n) ________, the distribution of sample means approaches a(n) ________ distribution.
A) decreases, uniform
B) increases, normal
C) decreases, normal
D) increases, uniform
E) increases, exponential
A) decreases, uniform
B) increases, normal
C) decreases, normal
D) increases, uniform
E) increases, exponential

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
36
For large samples, the sampling distribution of  is approximately normal with a mean of ________.
is approximately normal with a mean of ________.
A) μ
B) μ/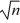
C)
D) z
 is approximately normal with a mean of ________.
is approximately normal with a mean of ________.A) μ
B) μ/
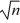
C)

D) z

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
37
Consider two population distributions labeled A and B. Distribution A is highly skewed and nonnormal, while distribution B is slightly skewed and near normal. In order for the sampling distributions of A and B to achieve the same degree of normality,
A) population A will require a larger sample size.
B) population B will require a larger sample size.
C) populations A and B will require the same sample size.
D) None of these answers is correct.
A) population A will require a larger sample size.
B) population B will require a larger sample size.
C) populations A and B will require the same sample size.
D) None of these answers is correct.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
38
If a population distribution is known to be normal, then it follows that
A) the sample mean must equal the population mean.
B) the sample mean must equal the population mean for large samples.
C) the sample standard deviation must equal the population standard deviation.
D) the sample mean must equal the population mean, the sample mean must equal the population mean for large samples, and the sample standard deviation must equal the population standard deviation.
E) None of these answers is correct.
A) the sample mean must equal the population mean.
B) the sample mean must equal the population mean for large samples.
C) the sample standard deviation must equal the population standard deviation.
D) the sample mean must equal the population mean, the sample mean must equal the population mean for large samples, and the sample standard deviation must equal the population standard deviation.
E) None of these answers is correct.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
39
Whenever the population has a normal distribution, the sampling distribution of  is a normal, or near normal, distribution
is a normal, or near normal, distribution
A) for only large sample sizes.
B) for only small sample sizes.
C) for any sample size.
D) for only samples of size 30 or more.
 is a normal, or near normal, distribution
is a normal, or near normal, distributionA) for only large sample sizes.
B) for only small sample sizes.
C) for any sample size.
D) for only samples of size 30 or more.

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
40
If the sampled population is finite and at least ________ times larger than the sample size, we treat the population as infinite.
A) 5
B) 20
C) 30
D) 10
A) 5
B) 20
C) 30
D) 10

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
41
An unbiased estimate of σ2 is ________.
A) s
B) s2
C)
D) σ
A) s
B) s2
C)

D) σ

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
42
Packages of sugar bags for Sweeter Sugar Inc. have an average weight of 16 ounces and a standard deviation of .2 ounces. The weights of the sugar packages are normally distributed. What is the probability that 16 randomly selected packages will have a weight in excess of 16.075 ounces?
A) .0500
B) .3520
C) .9332
D) .0668
A) .0500
B) .3520
C) .9332
D) .0668

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
43
Find P(  < 25) if μ = 16 and
< 25) if μ = 16 and 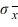 = 4.
= 4.
A) 1.000
B) 2.25
C) .9878
D) .0122
 < 25) if μ = 16 and
< 25) if μ = 16 and 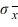 = 4.
= 4.A) 1.000
B) 2.25
C) .9878
D) .0122

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
44
The population of all ________ proportions is described by the sampling distribution of  .
.
A) population
B) random
C) observed
D) sample
 .
.A) population
B) random
C) observed
D) sample

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
45
Find P(  > 2,510) if μ = 2,500 and
> 2,510) if μ = 2,500 and 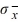 = 7.
= 7.
A) .0764
B) .9998
C) .9236
D) .0001
 > 2,510) if μ = 2,500 and
> 2,510) if μ = 2,500 and 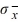 = 7.
= 7.A) .0764
B) .9998
C) .9236
D) .0001

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
46
The sampling distribution of the sample mean is a normal distribution for ________ sample sizes, regardless of the shape of the corresponding population distribution.
A) random
B) large
C) small
A) random
B) large
C) small

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
47
A random sample of size 36 is taken from a population with a mean of 50 and a standard deviation of 5. The sampling distribution of  ________.
________.
A) cannot be determined
B) is skewed to the left
C) is approximately normal
D) is skewed to the right
 ________.
________.A) cannot be determined
B) is skewed to the left
C) is approximately normal
D) is skewed to the right

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
48
Find P(  < 402), if μ = 400, σ = 200, and n = 100.
< 402), if μ = 400, σ = 200, and n = 100.
A) .8413
B) .4602
C) .5398
D) .1587
 < 402), if μ = 400, σ = 200, and n = 100.
< 402), if μ = 400, σ = 200, and n = 100.A) .8413
B) .4602
C) .5398
D) .1587

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
49
As the sample size ________, the standard deviation of the population of all sample proportions increases.
A) increases
B) stays the same
C) is variable
D) decreases
A) increases
B) stays the same
C) is variable
D) decreases

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
50
A theorem that allows us to use the normal probability distribution to approximate the sampling distribution of sample means and sample proportions whenever the sample size is large is known as ________.
A) cluster sampling
B) sampling error
C) sampling distribution of the mean
D) the Central Limit Theorem
A) cluster sampling
B) sampling error
C) sampling distribution of the mean
D) the Central Limit Theorem

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
51
The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.05 inches and a standard deviation of .3 inches. What is the probability that the average length of a steel sheet from a sample of 9 units is more than 29.95 inches long?
A) .8413
B) .6293
C) .3707
D) .1587
A) .8413
B) .6293
C) .3707
D) .1587

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
52
A golf tournament organizer is attempting to determine whether hole (pin) placement has a significant impact on the average number of strokes for the 13th hole on a given golf course. Historically, the pin has been placed in the front right corner of the green and the historical mean number of strokes for the hole has been 4.25, with a standard deviation of 1.6 strokes. On a particular day during the most recent golf tournament, the organizer placed the hole (pin) in the back left corner of the green. Sixty-four golfers played the hole with the new placement on that day. Determine the probability of the sample average number of strokes exceeding 4.75 using the historical mean and standard deviation.
A) .9938
B) .4013
C) .0062
D) .3783
A) .9938
B) .4013
C) .0062
D) .3783

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
53
Find P(  < 35) if μ = 40, σx = 16, n = 16.
< 35) if μ = 40, σx = 16, n = 16.
A) .9944
B) .4483
C) .5517
D) .1056
 < 35) if μ = 40, σx = 16, n = 16.
< 35) if μ = 40, σx = 16, n = 16.A) .9944
B) .4483
C) .5517
D) .1056

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
54
The ________ is the probability distribution of the population of all possible sample means that could be obtained from all possible samples of the same size.
A) sample mean
B) sampling Distribution of Sample Mean
C) probability
D) observations
A) sample mean
B) sampling Distribution of Sample Mean
C) probability
D) observations

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
55
Find σx, if μ = 400, P(  < 396) = .0228, and n = 100.
< 396) = .0228, and n = 100.
A) .20
B) 200
C) 20
D) 2.00
 < 396) = .0228, and n = 100.
< 396) = .0228, and n = 100.A) .20
B) 200
C) 20
D) 2.00

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
56
Find P(  > 172), if μ = 175 and
> 172), if μ = 175 and 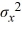 = 9.
= 9.
A) .1587
B) .8413
C) .6293
D) .3707
 > 172), if μ = 175 and
> 172), if μ = 175 and 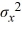 = 9.
= 9.A) .1587
B) .8413
C) .6293
D) .3707

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
57
As the sample size increases, the variability of the sampling distribution of the mean ________.
A) increases
B) stays the same
C) is variable
D) decreases
A) increases
B) stays the same
C) is variable
D) decreases

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
58
A random sample of size 1,000 is taken from a population where p = .20. Describe the sampling distribution of  .
.
A) cannot be determined
B) approximately normal
C) skewed to the left
D) skewed to the right
 .
.A) cannot be determined
B) approximately normal
C) skewed to the left
D) skewed to the right

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
59
Find P(395.4 <  < 404.6), if the population mean = 400, σ = 20, and n = 100.
< 404.6), if the population mean = 400, σ = 20, and n = 100.
A) .9786
B) .9999
C) .0214
D) .9893
 < 404.6), if the population mean = 400, σ = 20, and n = 100.
< 404.6), if the population mean = 400, σ = 20, and n = 100.A) .9786
B) .9999
C) .0214
D) .9893

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
60
The ________ is a minimum-variance unbiased point estimate of the mean of a normally distributed population.
A) sample mean
B) sample variance
C) sample standard deviation
D) observed mean
A) sample mean
B) sample variance
C) sample standard deviation
D) observed mean

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
61
A random sample of size 1,000 is taken from a population where p = .20. Find P(  < .22).
< .22).
A) .2643
B) .9431
C) .9207
D) .0571
 < .22).
< .22).A) .2643
B) .9431
C) .9207
D) .0571

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
62
A random sample of size 36 is taken from a population with mean 50 and standard deviation 5. Find P(  < 51.5).
< 51.5).
A) .9641
B) .0359
C) .1389
D) .9999
 < 51.5).
< 51.5).A) .9641
B) .0359
C) .1389
D) .9999

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
63
The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.05 inches and a standard deviation of .2 inches. A sample of 4 metal sheets is randomly selected from a batch. What is the probability that the average length of a sheet is between 30.25 and 30.35 inches long?
A) .9773
B) .0227
C) .0386
D) .0214
A) .9773
B) .0227
C) .0386
D) .0214

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
64
The number of defectives in 10 different samples of 50 observations each is the following: 5, 1, 1, 2, 3, 3, 1, 4, 2, 3. What is the estimate of the population proportion of defectives?
A) .25
B) .50
C) .05
D) .42
A) .25
B) .50
C) .05
D) .42

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
65
A random sample of size 1,000 is taken from a population where p = .20. Find P(  > .21).
> .21).
A) .2146
B) .0239
C) .9761
D) .7852
 > .21).
> .21).A) .2146
B) .0239
C) .9761
D) .7852

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
66
The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.05 inches and a standard deviation of .3 inches. What is the probability that the average length of a steel sheet from a sample of 9 steel sheets is more than 29.95 inches long?
A) .4602
B) .8413
C) .1587
D) .5397
A) .4602
B) .8413
C) .1587
D) .5397

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
67
A random sample of size 36 is taken from a population with mean 50 and standard deviation 5. Find P(  < 48).
< 48).
A) .0082
B) .8330
C) .0999
D) .1389
 < 48).
< 48).A) .0082
B) .8330
C) .0999
D) .1389

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
68
The population of lengths of aluminum-coated steel sheets is normally distributed with a mean of 30.05 inches and a standard deviation of .2 inches. What is the probability that a randomly selected sample of 4 sheets will have an average length of less than 29.9 inches long?
A) .0668
B) .9332
C) .0014
D) .4404
A) .0668
B) .9332
C) .0014
D) .4404

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
69
The number of defectives in 10 different samples of 100 observations each is the following: 1, 2, 1, 0, 2, 3, 1, 4, 2, 1. What is the estimate of the population proportion of defectives?
A) .017
B) .17
C) .016
D) .16
A) .017
B) .17
C) .016
D) .16

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
70
A random sample of size 1,000 is taken from a population where p = .20. What is 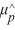 ?
?
A) .006
B) .20
C) .02
D) .16
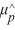 ?
?A) .006
B) .20
C) .02
D) .16

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
71
Packages of sugar bags for Sweeter Sugar Inc. have an average weight of 16 ounces and a standard deviation of .3 ounces. The weights of the sugar packages are normally distributed. What is the probability that 9 randomly selected packages will have an average weight in excess of 16.025 ounces?
A) .5987
B) .0062
C) .4013
D) .9938
A) .5987
B) .0062
C) .4013
D) .9938

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
72
Suppose that 60 percent of the voters in a particular region support a candidate. Find the probability that a sample of 1,000 voters would yield a sample proportion in favor of the candidate within 4 percentage points of the actual proportion.
A) .0155
B) .9952
C) .9484
D) .9902
A) .0155
B) .9952
C) .9484
D) .9902

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
73
A random sample of size 1,000 is taken from a population where p = .20. Find P(  > .175).
> .175).
A) .9759
B) .0239
C) .0392
D) .9999
 > .175).
> .175).A) .9759
B) .0239
C) .0392
D) .9999

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
74
A random sample of size 36 is taken from a population with mean 50 and standard deviation 5. Find P(  > 50.5).
> 50.5).
A) .0002
B) .7257
C) .2743
D) .1389
 > 50.5).
> 50.5).A) .0002
B) .7257
C) .2743
D) .1389

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
75
A random sample of size 36 is taken from a population with mean 50 and standard deviation 5. Find P(  > 49).
> 49).
A) .8331
B) .1151
C) .8849
D) .1389
 > 49).
> 49).A) .8331
B) .1151
C) .8849
D) .1389

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
76
A random sample of size 36 is taken from a population with mean 50 and standard deviation 5. What is μx?
A) 50
B) 5
C) 8.33
D) .833
A) 50
B) 5
C) 8.33
D) .833

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
77
A random sample of size 36 is taken from a population with mean 50 and standard deviation 5. What is 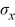 ?
?
A) .1389
B) 5
C) 8.33
D) .833
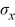 ?
?A) .1389
B) 5
C) 8.33
D) .833

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose that 60 percent of the voters in a particular region support a candidate. Find the probability that a sample of 1,000 voters would yield a sample proportion in favor of the candidate within 2 percentage points.
A) .9015
B) .8033
C) .0155
D) .7939
A) .9015
B) .8033
C) .0155
D) .7939

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
79
A random sample of size 1,000 is taken from a population where p = .20. Find P(  < .18).
< .18).
A) .9429
B) .0569
C) .2643
D) .0793
 < .18).
< .18).A) .9429
B) .0569
C) .2643
D) .0793

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck
80
A random sample of size 1,000 is taken from a population where p = .20. What is 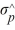 ?
?
A) .0051
B) .03162
C) .01414
D) .01265
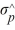 ?
?A) .0051
B) .03162
C) .01414
D) .01265

Unlock Deck
Unlock for access to all 111 flashcards in this deck.
Unlock Deck
k this deck


