Deck 18: Nonparametric Methods
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/103
Play
Full screen (f)
Deck 18: Nonparametric Methods
1
The Wilcoxon signed ranks test is also called the Mann-Whitney test.
False
2
If you have data that consist of matched pairs collected from two dependent populations, then it may be appropriate to use the Wilcoxon signed ranks test.
True
3
A parametric test is always more powerful than its nonparametric counterpart.
False
4
Which one of the following nonparametric methods can be used with a single population?
A) Spearman's test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test
A) Spearman's test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
5
The sign test is a test about a population median that is valid for any sample size and population shape.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
6
The Wilcoxon signed ranks test is a nonparametric test.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
7
The sign test is a nonparametric test for a population mean that is valid for any sample size and population shape.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
8
The Wilcoxon rank sum test is a nonparametric test used to compare the central tendencies of two populations when a paired difference experiment has been conducted.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
9
The Kruskal-Wallis test requires that all p samples being compared must have equal sample sizes.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
10
Which one of the following nonparametric methods can be used to compare more than two independent populations in a single test?
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test
E) Spearman's test
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test
E) Spearman's test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
11
The Wilcoxon rank sum test and the Kruskal-Wallis test both require that we take independent random samples.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
12
Parametric tests, such as F and t tests, are more powerful than their nonparametric counterparts if the assumptions needed to perform the parametric test are not violated.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
13
A sign test is a test of hypothesis about the population mean.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
14
An assumption of the Wilcoxon rank sum test is that the variances of the two populations are equal.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
15
Which one of the following nonparametric methods requires that we carry out a paired difference experiment?
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
16
In testing the significance of a population correlation coefficient using the Spearman's rank correlation coefficient, it is assumed that all possible combinations of values of variable X and variable Y have a bivariate normal probability distribution.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
17
The Spearman's rank correlation test can be used to study the relationship between two ordinal variables.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following statements about nonparametric methods is correct?
A) Nonparametric tests are only used in cases where parametric tests such as t or F do not exist.
B) Nonparametric tests should always be used when one is available, because they are easier to apply then their parametric counterparts.
C) Nonparametric tests are useful alternatives to parametric tests such as t or F when certain assumptions required by parametric tests are violated.
D) Nonparametric tests are only used if the data come from independent samples.
A) Nonparametric tests are only used in cases where parametric tests such as t or F do not exist.
B) Nonparametric tests should always be used when one is available, because they are easier to apply then their parametric counterparts.
C) Nonparametric tests are useful alternatives to parametric tests such as t or F when certain assumptions required by parametric tests are violated.
D) Nonparametric tests are only used if the data come from independent samples.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
19
Nonparametric tests can be more powerful than the corresponding t or F tests if the population distribution is highly skewed or nonnormal.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
20
The Wilcoxon rank sum test requires that two independent samples being compared must have equal sample sizes.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
21
Assume that the following data set is not normally distributed. (21, 18, 4, 9, 14, 16, 17, 12, 15, 8, 7, 5)
If Ha: Md > 6, then the p value is
A) .0161.
B) .0029.
C) .0537.
D) .0322.
E) .0192.
If Ha: Md > 6, then the p value is
A) .0161.
B) .0029.
C) .0537.
D) .0322.
E) .0192.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
22
Assume that the following data set is not normally distributed. (21, 18, 4, 9, 14, 16, 17, 12, 15, 8, 7, 5)
If Ha: Md ≠ 7, then the p value is
A) .0161.
B) .0029.
C) .1458.
D) .0729.
E) .0537.
If Ha: Md ≠ 7, then the p value is
A) .0161.
B) .0029.
C) .1458.
D) .0729.
E) .0537.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
23
The Kruskal-Wallis test is the nonparametric counterpart of the
A) large-sample test about a single population mean.
B) two independent samples t test.
C) one-way ANOVA F test.
D) paired-difference t test.
E) F test for equality of population variances.
A) large-sample test about a single population mean.
B) two independent samples t test.
C) one-way ANOVA F test.
D) paired-difference t test.
E) F test for equality of population variances.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
24
The signed ranks test is the nonparametric counterpart of the
A) small-sample t test about a single population mean.
B) two independent samples t test.
C) one-way ANOVA F test.
D) paired difference t test.
E) F test for equality of population variances.
A) small-sample t test about a single population mean.
B) two independent samples t test.
C) one-way ANOVA F test.
D) paired difference t test.
E) F test for equality of population variances.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
25
A copy machine service company provides maintenance and repair service for different types and brands of copiers. The manager of the repair department wants to know if the repair time for brand A is higher than the repair time for brand B. The manager randomly selects eight repair records associated with brand A and eight repair records associated with brand B. The distribution of repair times for both brand A and brand B is highly skewed. Which one of the following nonparametric tests is appropriate for this problem?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
26
Parametric methods are ________ more powerful than their nonparametric counterparts.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
27
Assume that the following data set is not normally distributed. (21, 18, 4, 9, 14, 16, 17, 12, 15, 8, 7, 5)
If Ha: Md < 6, then the value of S is
A) 0.
B) 1.
C) 2.
D) 3.
E) 4.
If Ha: Md < 6, then the value of S is
A) 0.
B) 1.
C) 2.
D) 3.
E) 4.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
28
In a manufacturing facility producing fasteners, a foreman suspects that the diameter of the bolts produced by his second-shift workers is greater than the diameter of the bolts produced by his first-shift workers. He takes a sample of five bolts from the first shift and a sample of four bolts from the second shift and measures the diameters in inches. The population of bolt diameter measurements is not normally distributed. Which one of the following nonparametric tests is appropriate for this problem?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
29
Five years ago, the average starting salary of a new college graduate with a major in marketing was $34,000. A random sample of 10 graduates from this year's graduating class of a local university yielded the following starting salaries in thousands of dollars: 38, 36, 25, 37, 35, 24, 38, 45, 39, 36. The local university wants to determine if the starting salaries have increased in the last five years. Assume that the population of starting salaries in marketing is not normally distributed. Which one of the following tests is appropriate for this problem?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Mann-Whitney test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Mann-Whitney test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
30
Two NFL scouts are in the process of recruiting seven college senior football receivers. After a careful review and evaluation, both scouts ranked the seven receivers in terms of their professional career prospects. If we want to determine whether the two scouts have similar opinions about the professional football career prospects of the seven players, which one of the following nonparametric tests would we choose?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
31
The Wilcoxon signed ranks test is the nonparametric counterpart of the
A) large sample test about a single population mean.
B) two independent samples t test.
C) one-way ANOVA F test.
D) paired difference t test.
E) F test for equality of population variances.
A) large sample test about a single population mean.
B) two independent samples t test.
C) one-way ANOVA F test.
D) paired difference t test.
E) F test for equality of population variances.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
32
An e-business/e-commerce information technology consulting company wants to compare the effectiveness of three programming languages that its programmers use. Currently each programming language is used by approximately 1/3 of the programmers employed by the company. The director of the programming division randomly selected five programmers from the users of each of the three programming languages and assigned the same simple programming task to each programmer. It is known that all three populations have highly skewed distributions with extreme outliers. Which one of the following nonparametric tests is appropriate for this problem?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
33
The Wilcoxon rank sum test is the nonparametric counterpart of the
A) large-sample test about a single population mean.
B) two independent samples t test.
C) F test.
D) paired-difference t test.
E) F test for equality of population variances.
A) large-sample test about a single population mean.
B) two independent samples t test.
C) F test.
D) paired-difference t test.
E) F test for equality of population variances.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
34
The ________ detects whether the probability distribution of one population is shifted to the right or to the left of the probability distribution of another population.
A) sign test
B) Wilcoxon rank sum test
C) Wilcoxon signed ranks test
D) Kruskal-Wallis test
A) sign test
B) Wilcoxon rank sum test
C) Wilcoxon signed ranks test
D) Kruskal-Wallis test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
35
The EPA has stipulated that the Pollution Standard Index (PSI) for clean air standards is to average no more than 100. A random sample of nine days for the city of Acorn showed PSI readings of 144, 85, 90, 120, 150, 105, 93, 130, and 115. Assume the population of PSI readings is highly nonnormal. The EPA wants to determine if there is significant evidence to conclude that Acorn's air is dirtier than the stipulated clean air standards. Which one of the following tests is appropriate for this problem?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
36
Assume that the following data set is not normally distributed. (21, 18, 4, 9, 14, 16, 17, 12, 15, 8, 7, 5)
If Ha: Md < 16, then the p value is
A) .1208.
B) .1937.
C) .0537.
D) .3874.
E) .1458.
If Ha: Md < 16, then the p value is
A) .1208.
B) .1937.
C) .0537.
D) .3874.
E) .1458.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
37
Refer to the MegaStat/Excel output for the Wilcoxon rank sum test given in the table below. 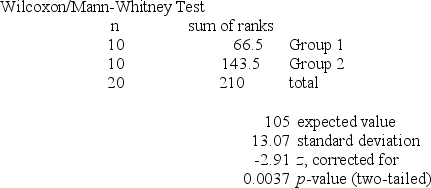 At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?
At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?
H0: D1 and D2 are identical probability distributions.
A) We reject H0 and conclude there is very strong evidence that the median value of the first sample significantly differs from the median value of the second sample.
B) We reject H0 and conclude there is very strong evidence that the median value of the first sample is significantly less than the median value of the second sample.
C) We do not reject H0 and conclude there is not sufficient evidence that the median value of the first sample is significantly less than the median value of the second sample.
D) We do not reject H0 and conclude there is insufficient evidence to conclude that the median value of the first sample is not significantly different from the median value of the second sample.
E) We do not reject H0 and conclude there is very strong evidence that the median value of the first sample is significantly greater than the median value of the second sample.
 At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?
At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?H0: D1 and D2 are identical probability distributions.
A) We reject H0 and conclude there is very strong evidence that the median value of the first sample significantly differs from the median value of the second sample.
B) We reject H0 and conclude there is very strong evidence that the median value of the first sample is significantly less than the median value of the second sample.
C) We do not reject H0 and conclude there is not sufficient evidence that the median value of the first sample is significantly less than the median value of the second sample.
D) We do not reject H0 and conclude there is insufficient evidence to conclude that the median value of the first sample is not significantly different from the median value of the second sample.
E) We do not reject H0 and conclude there is very strong evidence that the median value of the first sample is significantly greater than the median value of the second sample.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
38
Which one of the following nonparametric methods can be used to determine the strength of the relationship between two variables?
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test
E) Spearman's test
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Wilcoxon rank sum test
E) Spearman's test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
39
A cholesterol test was given to 10 heart patients with high cholesterol levels. The same 10 heart patients are then given a new cholesterol-reducing drug for six months. Before the patients begin taking the drug, they are told to maintain their current diets and eating habits so that the effect of the drug can be more effectively determined. After taking the drug for six months, the same patients are given a cholesterol test again. The pharmaceutical company manufacturing the medicine wants to know if the drug is effective in reducing the cholesterol levels of the patients. The cholesterol levels before and after taking the drug are recorded for each patient. The population of cholesterol levels is not normally distributed. Which one of the following nonparametric tests is appropriate for this problem?
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test
A) Wilcoxon signed ranks test
B) Wilcoxon rank sum test
C) sign test
D) Kruskal-Wallis test
E) Spearman's rank correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
40
Which one of the following nonparametric methods can be considered as an extension of the Wilcoxon rank sum test?
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Spearman's test
A) Wilcoxon signed ranks test
B) sign test
C) Kruskal-Wallis test
D) Spearman's test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
41
When a large sample is taken, the ________ approximation to the binomial distribution can be used to implement the sign test.
A) chi-square
B) normal
C) correlation coefficient
D) rank sum
A) chi-square
B) normal
C) correlation coefficient
D) rank sum

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
42
In order to perform the ________, all of the observations in p samples are combined into a single set and all of the values in the single set are ranked from smallest to largest. After ranking, the sum of the ranks for each of the p samples is calculated.
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
43
In order to perform the ________, all of the observations in two samples are combined into a single set and all of the values in the single set are ranked from smallest to largest.
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
44
Refer to the MegaStat/Excel output for the Wilcoxon rank sum test given in the table below. 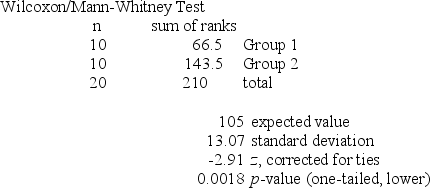 At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.
At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.
A) We reject H0 and conclude that there is very strong evidence that the median value of the first sample significantly differs from the median value of the second sample.
B) We reject H0 and conclude that there is very strong evidence that the median value of the first sample is significantly less than the median value of the second sample.
C) We do not reject H0 and conclude there is not sufficient evidence that the median value of the first sample is significantly less than the median value of the second sample.
D) We do not reject H0 and conclude there is not sufficient evidence to conclude that the median value of the first sample is not significantly different than the median value of the second sample.
E) We do not reject H0 and conclude there is very strong evidence that the median value of the first sample is significantly less than the median value of the second sample.
 At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.
At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.A) We reject H0 and conclude that there is very strong evidence that the median value of the first sample significantly differs from the median value of the second sample.
B) We reject H0 and conclude that there is very strong evidence that the median value of the first sample is significantly less than the median value of the second sample.
C) We do not reject H0 and conclude there is not sufficient evidence that the median value of the first sample is significantly less than the median value of the second sample.
D) We do not reject H0 and conclude there is not sufficient evidence to conclude that the median value of the first sample is not significantly different than the median value of the second sample.
E) We do not reject H0 and conclude there is very strong evidence that the median value of the first sample is significantly less than the median value of the second sample.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
45
A professional organization is attempting to determine whether salaries of hospital CFOs differ by geographical region. Five hospital CFOs were randomly selected from each of the following four regions of the United States: East, Midwest, South, and West. Each CFO was then asked his or her annual salary. The salary distributions were highly skewed. The table below summarizes the results of the Kruskal-Wallis test obtained from MegaStat/Excel. Kruskal-Wallis Test
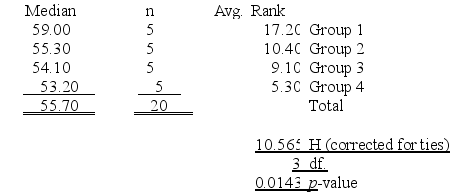 At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?
At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?
H0: The four populations under consideration have identical salaries.
A) We reject H0 and conclude that there is very strong evidence that the median hospital CFO salaries differ among all four regions in the United States.
B) We failed to reject H0 and conclude that there is not sufficient evidence that the median hospital CFO salaries differ among any of the four regions of the United States.
C) We do not reject H0 and conclude that there is only adequate evidence that the median hospital CFO salaries differ between at least two of the four regions in the United States.
D) We reject H0 and conclude that there is strong evidence that the median hospital CFO salaries differ between at least two of the four regions in the United States.
E) We do not reject H0 and conclude that all four populations under consideration are identical in their locations.
 At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?
At a significance level of .05, which one of the following statements is correct regarding the following null hypothesis?H0: The four populations under consideration have identical salaries.
A) We reject H0 and conclude that there is very strong evidence that the median hospital CFO salaries differ among all four regions in the United States.
B) We failed to reject H0 and conclude that there is not sufficient evidence that the median hospital CFO salaries differ among any of the four regions of the United States.
C) We do not reject H0 and conclude that there is only adequate evidence that the median hospital CFO salaries differ between at least two of the four regions in the United States.
D) We reject H0 and conclude that there is strong evidence that the median hospital CFO salaries differ between at least two of the four regions in the United States.
E) We do not reject H0 and conclude that all four populations under consideration are identical in their locations.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
46
The Wilcoxon rank sum test is used to compare the locations of two ________ populations.
A) dependent
B) normal
C) independent
D) similar
A) dependent
B) normal
C) independent
D) similar

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
47
A professional organization is attempting to determine whether salaries of hospital CFOs differ by geographical region. Five hospital CFOs were randomly selected from each of the following four regions of the United States: East, Midwest, South, and West. Each CFO was then asked his or her annual salary. The salary distributions were highly skewed. The table below summarizes the results of the Kruskal-Wallis test obtained from MegaStat/Excel. Kruskal-Wallis Test
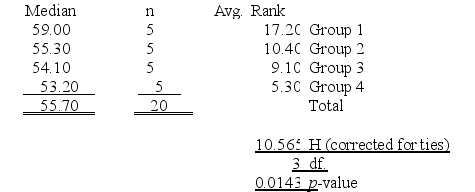 At a significance level of .05, the rejection point condition for the hypothesis test is
At a significance level of .05, the rejection point condition for the hypothesis test is
A) reject H0 if χ2 > 9.3484.
B) reject H0 if χ2 > 30.1435.
C) reject H0 if χ2 > 7.81473.
D) reject H0 if χ2 > .341846.
E) reject H0 if χ2 > 32.8523.
 At a significance level of .05, the rejection point condition for the hypothesis test is
At a significance level of .05, the rejection point condition for the hypothesis test isA) reject H0 if χ2 > 9.3484.
B) reject H0 if χ2 > 30.1435.
C) reject H0 if χ2 > 7.81473.
D) reject H0 if χ2 > .341846.
E) reject H0 if χ2 > 32.8523.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
48
The Kruskal-Wallis H statistic can be approximated by the ________ distribution.
A) normal
B) chi-square
C) z
D) t
A) normal
B) chi-square
C) z
D) t

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
49
Wax-com Electronics Inc. claims that a certain circuit board has a median operating life of less than 20,000 hours. A random sample of 25 such circuit boards showed 8 circuit boards failing before 20,000 hours and 17 circuit boards failing after 20,000 hours. Assume the useful life of the circuit board is not normally distributed and state the null hypothesis.
A) H0: Md ≥ 20,000
B) H0: Md ≤ 20,000
C) H0: Md < 20,000
D) H0: Md ≠ 20,000
A) H0: Md ≥ 20,000
B) H0: Md ≤ 20,000
C) H0: Md < 20,000
D) H0: Md ≠ 20,000

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
50
Refer to the MegaStat/Excel output for the Wilcoxon signed ranks test given in the table below.  At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.
At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.
A) T − ≤ 2
B) T + ≤ 2
C) T − ≤ 0
D) T − ≤ 6
E) The smaller of T + or T − is less than 8.
 At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.
At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2.A) T − ≤ 2
B) T + ≤ 2
C) T − ≤ 0
D) T − ≤ 6
E) The smaller of T + or T − is less than 8.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
51
In a Wilcoxon rank sum test, when two or more observations are equal, we assign to each tied observation a rank equal to the ________ of the consecutive ranks.
A) average
B) median
C) sum
D) difference
A) average
B) median
C) sum
D) difference

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
52
In a local ice-skating contest, there were two judges and 15 contestants. Each judge was asked to rate each contestant on a 7-point scale. The most successful candidates received a rating value of 7, while the least successful candidates received a rating value of 1. It appears that the bivariate normal probability distribution assumption was severely violated. The City Council wants to know whether the judges have similar opinions in rating ice-skating competitors. At a significance level of .01, the rejection point condition for the hypothesis test is
A) reject H0 if rs > .457.
B) reject H0 if rs > .623.
C) reject H0 if rs > .441.
D) reject H0 if rs > .646.
E) reject H0 if rs > .689.
A) reject H0 if rs > .457.
B) reject H0 if rs > .623.
C) reject H0 if rs > .441.
D) reject H0 if rs > .646.
E) reject H0 if rs > .689.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
53
Refer to the MegaStat/Excel output for the Wilcoxon signed ranks test given in the table below.  At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left or right of D2.
At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left or right of D2.
A) We reject H0 and conclude there is not sufficient evidence that the probability distribution of population 1 is shifted to the left of the probability distribution of population 2.
B) We cannot reject H0 and conclude there is not sufficient evidence that the probability distribution of population 1 is shifted to the left or right of the probability distribution of population 2.
C) We reject H0 and conclude there is very strong evidence that the probability distribution of population 1 is shifted to the left of the probability distribution of population 2.
D) We do not reject H0 and conclude there is very strong evidence that the probability distribution of population 1 is shifted to the left or to the right of the probability distribution of population 2.
E) We do not reject H0 and conclude there is very strong evidence that the probability distribution of population 1 is identical to the probability distribution of population 2.
 At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left or right of D2.
At a significance level of .01, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left or right of D2.A) We reject H0 and conclude there is not sufficient evidence that the probability distribution of population 1 is shifted to the left of the probability distribution of population 2.
B) We cannot reject H0 and conclude there is not sufficient evidence that the probability distribution of population 1 is shifted to the left or right of the probability distribution of population 2.
C) We reject H0 and conclude there is very strong evidence that the probability distribution of population 1 is shifted to the left of the probability distribution of population 2.
D) We do not reject H0 and conclude there is very strong evidence that the probability distribution of population 1 is shifted to the left or to the right of the probability distribution of population 2.
E) We do not reject H0 and conclude there is very strong evidence that the probability distribution of population 1 is identical to the probability distribution of population 2.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
54
The ________ is a nonparametric method that requires data consisting of matched pairs.
A) Wilcoxon rank sum test
B) Kruskal-Wallis test
C) Wilcoxon signed ranks test
D) sign test
A) Wilcoxon rank sum test
B) Kruskal-Wallis test
C) Wilcoxon signed ranks test
D) sign test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
55
A ________ can be used without assuming that the sampled population(s) has/have a particular type of probability distribution.
A) t- test
B) nonparametric test
C) linear regression test
D) correlation test
A) t- test
B) nonparametric test
C) linear regression test
D) correlation test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
56
The ________ is a nonparametric counterpart of a one-way ANOVA F test.
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
57
If the population from which we sample is highly skewed to the right or to the left, then the population ________ might be a better measure of central tendency than the population mean.
A) median
B) variance
C) mode
D) average
A) median
B) variance
C) mode
D) average

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
58
The ________ is a nonparametric counterpart of a small-sample t test for comparing two independent population locations.
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test
A) Wilcoxon rank sum test
B) Kruskal-Wallis H test
C) Wilcoxon signed ranks test
D) sign test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
59
Refer to the MegaStat/Excel output for the Wilcoxon rank sum test given in the table below. 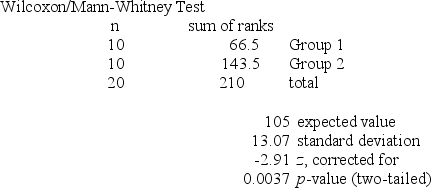 At a significance level of .05, which one of the following rejection point conditions is correct regarding the following null hypothesis?
At a significance level of .05, which one of the following rejection point conditions is correct regarding the following null hypothesis?
H0: D1 and D2 are identical probability distributions.
A) Reject H0 if T ≥ 79 or T ≤ 131.
B) Reject H0 if T ≥ 131 or T ≤ 83.
C) Reject H0 if T ≥ 131 or T ≤ 79.
D) Reject H0 if T ≤ 83 or T ≥ 127.
E) Reject H0 if T ≤ 79 or T ≥ 127.
 At a significance level of .05, which one of the following rejection point conditions is correct regarding the following null hypothesis?
At a significance level of .05, which one of the following rejection point conditions is correct regarding the following null hypothesis?H0: D1 and D2 are identical probability distributions.
A) Reject H0 if T ≥ 79 or T ≤ 131.
B) Reject H0 if T ≥ 131 or T ≤ 83.
C) Reject H0 if T ≥ 131 or T ≤ 79.
D) Reject H0 if T ≤ 83 or T ≥ 127.
E) Reject H0 if T ≤ 79 or T ≥ 127.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
60
Refer to the MegaStat/Excel output for the Wilcoxon rank sum test given in the table below. 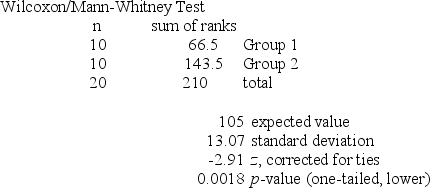 At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2
At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2
A) Reject H0 if T ≥ 83.
B) Reject H0 if T ≤ 127.
C) Reject H0 if T ≥ 131.
D) Reject H0 if T ≤ 83.
E) Reject H0 if T ≤ 79.
 At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2
At a significance level of .05, which one of the following rejection point conditions is correct regarding the null hypothesis, H0: D1 and D2 are identical probability distributions, and the alternative hypothesis of Ha: D1 is shifted to the left of D2A) Reject H0 if T ≥ 83.
B) Reject H0 if T ≤ 127.
C) Reject H0 if T ≥ 131.
D) Reject H0 if T ≤ 83.
E) Reject H0 if T ≤ 79.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
61
Five years ago, the average starting salary of a new college graduate with a major in marketing was $34,000. A random sample of 10 graduates from this year's graduating class of a local university yielded the following starting salaries in thousands of dollars: 28, 36, 25, 37, 35, 24, 38, 45, 39, 36. The local university wants to determine if the median starting salary for marketing graduates has increased in the last five years. Assume that the population of starting salaries in marketing is not normally distributed. Using α = .05, can we conclude that the starting salaries increased in the last five years?
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
62
An international economist believes that there is a significant relationship between the amount of debt and the rate of unemployment. He randomly selected six countries to determine if there is a significant relationship between debt and unemployment rate. In the following table, debt figures for the six countries are given in billions of dollars and the corresponding unemployment rate is given in percentages. He also discovered that both the distribution of debt and the distribution of unemployment rate were highly skewed. Use Spearman's rank correlation and determine if there is a significant correlation between debt and unemployment rate at alpha .05. Show the rank correlation. 
A) rs = .914, reject the null hypothesis.
B) rs = .886, do not reject the null hypothesis.
C) rs = .886, reject the null hypothesis.
D) rs = .914, do not reject the null hypothesis.

A) rs = .914, reject the null hypothesis.
B) rs = .886, do not reject the null hypothesis.
C) rs = .886, reject the null hypothesis.
D) rs = .914, do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
63
Five years ago, the average starting salary of a new college graduate with a major in marketing was $34,000. A random sample of 10 graduates from this year's graduating class of a local university yielded the following starting salaries in thousands of dollars: 28, 36, 25, 37, 35, 24, 38, 45, 39, 36. The local university wants to determine if the median starting salary for marketing graduates has increased in the last five years. Assume that the population of starting salaries in marketing is not normally distributed. The p value is found to be .0547. Using α = .10, can we conclude that the starting salaries increased in the last five years?
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
64
Five years ago, the average starting salary of a new college graduate with a major in marketing was $34,000. A random sample of 10 graduates from this year's graduating class of a local university yielded the following starting salaries in thousands of dollars: 28, 36, 25, 37, 35, 24, 38, 45, 39, 36. The local university wants to determine if the median starting salary for marketing graduates has increased in the last five years. State the alternative hypothesis. Assume that the population of starting salaries in marketing is not normally distributed.
A) HA: Md < 34,000
B) HA: Md > 34,000
C) HA: Md ≠ 34,000
D) HA: Md = 34,000
A) HA: Md < 34,000
B) HA: Md > 34,000
C) HA: Md ≠ 34,000
D) HA: Md = 34,000

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
65
A cholesterol test was given to ten heart patients with high cholesterol levels. The same ten heart patients are then given a new cholesterol-reducing drug for six months. Before the patients begin taking the drug, they are told to maintain their current diets and eating habits so that the effect of the drug can be more effectively determined. After taking the drug for six months, the same patients are given a cholesterol test again. The cholesterol levels before and after taking the drug are given below. The cholesterol level readings are not normally distributed. At α = .05, test to determine if the drug is helpful in reducing cholesterol levels. 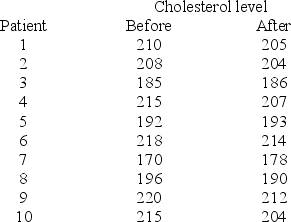
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.

A) Reject the null hypothesis.
B) Do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
66
Three years ago, a major hotel chain purchased a large number of heating and air-conditioning units from three major manufacturers, A, B, and C. The accounting department of the hotel chain kept records on their repair and replacement costs over the last three years. The manager of the purchasing department randomly selected six brand A, seven brand B, and six brand C heating and air-conditioning unit records. The repair and replacement costs in dollars are summarized in the following table. At α = .05, can we conclude that there is a significant difference in repair costs among the three brands? 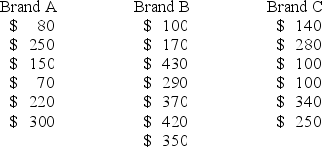
A) Reject the null hypothesis.
B) Fail to reject the null hypothesis.
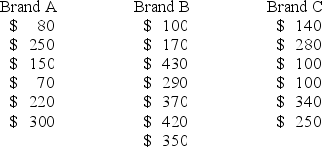
A) Reject the null hypothesis.
B) Fail to reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
67
Two NFL scouts are in the process of recruiting seven college senior football players (receivers). After a careful review and evaluation, both scouts ranked the seven receivers in terms of their professional career prospects. The rankings are given below.  At α = .05, does it appear that the two scouts have similar opinions about the professional football career prospects of the seven players (positive correlation vs. no correlation)?
At α = .05, does it appear that the two scouts have similar opinions about the professional football career prospects of the seven players (positive correlation vs. no correlation)?
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.
 At α = .05, does it appear that the two scouts have similar opinions about the professional football career prospects of the seven players (positive correlation vs. no correlation)?
At α = .05, does it appear that the two scouts have similar opinions about the professional football career prospects of the seven players (positive correlation vs. no correlation)?A) Reject the null hypothesis.
B) Do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
68
Wax-com Electronics Inc. claims that a certain circuit board has a median operating life of less than 20,000 hours. A random sample of 25 such circuit boards showed 8 circuit boards failing before 20,000 hours and 17 circuit boards failing after 20,000 hours. Assume the useful life of the circuit board is not normally distributed. At α = .05, can it be concluded that the sample contradicts the company's claim? Assume the useful life of the circuit board is not normally distributed.
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
69
An e-business/e-commerce information technology consulting company wants to compare the effectiveness of three programming languages that its programmers use. Currently each programming language is used by approximately 1/3 of the company's programmers. The director of the programming division randomly selected five programmers from the users of each of the three programming languages and assigned the same simple programming task to each programmer. All three populations have highly skewed distributions with extreme outliers. The rank sum values for each of the programming groups are T1 = 23, T2 = 48, and T3 = 49. At α = .05, does the median time required to program a simple task differ between the three different programming languages?
A) H = 4.34, reject the null hypothesis.
B) H = 4.34, do not reject the null hypothesis.
C) H = 5.99, reject the null hypothesis.
D) H = 5.99, do not reject the null hypothesis.
A) H = 4.34, reject the null hypothesis.
B) H = 4.34, do not reject the null hypothesis.
C) H = 5.99, reject the null hypothesis.
D) H = 5.99, do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
70
In a manufacturing facility producing fasteners, a foreman suspects that the diameter of the bolts produced by his first-shift workers is greater than the diameter of the bolts produced by his second-shift workers. He takes a sample of five bolts from the first shift and a sample of four bolts from the second shift and measures the diameters in inches. Below are the results from five first-shift and four second-shift observations. The bolt diameter measurements are not normally distributed.  At α = .05, can we conclude that his suspicion is correct?
At α = .05, can we conclude that his suspicion is correct?
A) Reject the null hypothesis, the diameter is greater for first shift versus second shift.
B) Do not reject the null hypothesis; there is no evidence that the diameters differ by shift.
 At α = .05, can we conclude that his suspicion is correct?
At α = .05, can we conclude that his suspicion is correct?A) Reject the null hypothesis, the diameter is greater for first shift versus second shift.
B) Do not reject the null hypothesis; there is no evidence that the diameters differ by shift.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
71
The EPA has stipulated that the Pollution Standard Index (PSI) for clean air standards is to average no more than 100. A random sample of 9 days for the city of Acme showed PSI readings of 144, 85, 90, 120, 150, 105, 93, 130, and 115. The EPA wants to test to determine if Acme air is dirtier than the stipulated clean air standards. Assume the population of PSI readings is highly nonnormal and state the null hypothesis.
A) H0: Md ≥ 100
B) H0: Md ≤ 100
C) H0: Md ≠ 100
D) H0: Md > 100
A) H0: Md ≥ 100
B) H0: Md ≤ 100
C) H0: Md ≠ 100
D) H0: Md > 100

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
72
A copy machine service company provides maintenance and repair service for different types and brands of copiers. The manager of the repair department wants to know if the repair time for brand A is higher than the repair time for brand B. The manager randomly selected eight repair records associated with brand A and eight repair records associated with brand B. The repair times (in minutes) for both samples are given below. The distribution of repair times for both brand A and brand B is highly skewed. 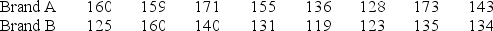 On average, can it be concluded that the repair time for brand A is significantly higher than the repair time for brand B? Test at α = .05.
On average, can it be concluded that the repair time for brand A is significantly higher than the repair time for brand B? Test at α = .05.
A) Reject the null hypothesis.
B) Fail to reject the null hypothesis.
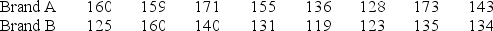 On average, can it be concluded that the repair time for brand A is significantly higher than the repair time for brand B? Test at α = .05.
On average, can it be concluded that the repair time for brand A is significantly higher than the repair time for brand B? Test at α = .05.A) Reject the null hypothesis.
B) Fail to reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
73
In an effort to improve productivity in its factory, a firm recently instituted a training program for its workers. One of the work crews consisted of 14 workers. Seven workers from this crew were selected at random to attend the training course. All seven workers selected successfully completed the training course. The remaining seven workers served as a control group and did not attend the training course. Three months after the training course, a foreman who did not know which employees attended the training course was asked to rank all 14 employees in terms of their productivity. A rank of 14 indicates the most productive employee in the crew, while a rank of 1 indicates the least productive worker.  State the null hypothesis for this problem.
State the null hypothesis for this problem.
A) H0: DT ≤ DU
B) H0: DT ≥ DU
C) H0: DT ≠ DU
D) H0: DT > DU
 State the null hypothesis for this problem.
State the null hypothesis for this problem.A) H0: DT ≤ DU
B) H0: DT ≥ DU
C) H0: DT ≠ DU
D) H0: DT > DU

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
74
An e-business/e-commerce information technology consulting company wants to compare the effectiveness of three programming languages that its programmers use. Currently each programming language is used by approximately 1/3 of the programmers employed by the company. The director of the programming division randomly selected five programmers from the users of each of the three programming languages and assigned the same simple programming task to each programmer. It is known that all three populations have highly skewed distributions with extreme outliers. Calculate the value of Ti (rank sum) for Program B. 
A) 23
B) 48
C) 49
D) 57

A) 23
B) 48
C) 49
D) 57

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
75
A copy machine service company provides maintenance and repair service for different types and brands of copiers. The manager of the repair department wants to know if the repair time for brand A is higher than the repair time for brand B. The manager randomly selected eight repair records associated with brand A and eight repair records associated with brand B. The repair times (in minutes) for both samples are given below. The distribution of repair times for both brand A and brand B is highly skewed. 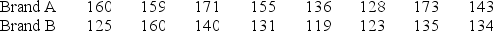 What is the appropriate alternative hypothesis for this problem?
What is the appropriate alternative hypothesis for this problem?
A) HA: DA is shifted to the left or right of DB
B) HA: DA is shifted to the right of DB
C) HA: DA is shifted to the left of DB
D) HA: DA is equal to DB
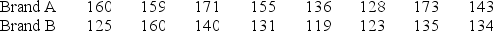 What is the appropriate alternative hypothesis for this problem?
What is the appropriate alternative hypothesis for this problem?A) HA: DA is shifted to the left or right of DB
B) HA: DA is shifted to the right of DB
C) HA: DA is shifted to the left of DB
D) HA: DA is equal to DB

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
76
A cholesterol test was given to 10 heart patients with high cholesterol levels. The same 10 heart patients are then given a new cholesterol-reducing drug for six months. Before the patients begin taking the drug, they are told to maintain their current diets and eating habits so that the effect of the drug can be more effectively determined. After taking the drug for six months, the same patients are given a cholesterol test again. The pharmaceutical company that manufactures the drug wants to determine if the drug is helpful in reducing cholesterol levels. The cholesterol level readings are not normally distributed. State the alternative hypothesis for this problem.
A) The probability distribution of cholesterol readings of patients before and after the trials is identical.
B) The probability distribution of cholesterol readings at the end of six months has shifted to the left of the probability distribution of cholesterol readings at the beginning of the trials.
C) The probability distribution of cholesterol readings at the end of six months has shifted to the right of the probability distribution of cholesterol readings at the beginning of the trials.
D) The probability distribution of cholesterol readings of patients at the end of six months has shifted to the right or left of the probability distribution of cholesterol readings at the beginning of the trials.
A) The probability distribution of cholesterol readings of patients before and after the trials is identical.
B) The probability distribution of cholesterol readings at the end of six months has shifted to the left of the probability distribution of cholesterol readings at the beginning of the trials.
C) The probability distribution of cholesterol readings at the end of six months has shifted to the right of the probability distribution of cholesterol readings at the beginning of the trials.
D) The probability distribution of cholesterol readings of patients at the end of six months has shifted to the right or left of the probability distribution of cholesterol readings at the beginning of the trials.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
77
The EPA has stipulated that the Pollution Standard Index (PSI) for clean air standards is to average no more than 100. A random sample of 9 days for the city of Acme showed PSI readings of 144, 85, 90, 120, 150, 105, 93, 130, and 115. Assume the population of PSI readings is highly nonnormal. Is there significant evidence to conclude that Acme air is dirtier than the stipulated clean air standards? Test at α = .05.
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.
A) Reject the null hypothesis.
B) Do not reject the null hypothesis.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
78
Two NFL scouts are in the process of recruiting seven college senior football players receivers. After a careful review and evaluation, both scouts ranked the seven receivers in terms of their professional career prospects. If we want to determine whether the two scouts have similar opinions about the professional football career prospects of the seven players, state the null hypothesis.
A) H0: ρs ≠ 0
B) H0: ρs ≥ 0
C) H0: ρs ≤ 0
D) H0: ρs = 0
A) H0: ρs ≠ 0
B) H0: ρs ≥ 0
C) H0: ρs ≤ 0
D) H0: ρs = 0

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
79
The EPA has stipulated that the Pollution Standard Index (PSI) for clean air standards is to average no more than 100. A random sample of 9 days for the city of Acme showed PSI readings of 144, 85, 90, 120, 150, 105, 93, 130, and 115.Assume the population of PSI readings is highly nonnormal. The EPA wants to determine if there is significant evidence to conclude that Acme air is dirtier than the stipulated clean air standards. The test is conducted at α = .05 and the p value is found to be .254. Based on this result, provide a one-sentence managerial conclusion.
A) Acme air is dirtier than the EPA stipulated clean air standards.
B) We cannot conclude that Acme air is dirtier than the EPA stipulated clean air standards.
C) Acme air is better than the EPA stipulated clean air standards.
D) Acme air meets the EPA stipulated clean air standards.
A) Acme air is dirtier than the EPA stipulated clean air standards.
B) We cannot conclude that Acme air is dirtier than the EPA stipulated clean air standards.
C) Acme air is better than the EPA stipulated clean air standards.
D) Acme air meets the EPA stipulated clean air standards.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
80
In an effort to improve productivity in its factory, a firm recently instituted a training program for its workers. One of the work crews consisted of 14 workers. Seven workers from this crew were selected at random to attend the training course. All seven workers selected successfully completed the training course. The remaining seven workers served as a control group and did not attend the training course. Three months after the training course, a foreman who did not know which employees attended the training course was asked to rank all 14 employees in terms of their productivity. A rank of 14 indicates the most productive employee in the crew, while a rank of 1 indicates the least productive worker.  At α = .05, can it be concluded that training was beneficial in improving productivity?
At α = .05, can it be concluded that training was beneficial in improving productivity?
A) Reject the null hypothesis; training is beneficial.
B) Do not reject the null hypothesis; we cannot determine if the training makes a difference.
 At α = .05, can it be concluded that training was beneficial in improving productivity?
At α = .05, can it be concluded that training was beneficial in improving productivity?A) Reject the null hypothesis; training is beneficial.
B) Do not reject the null hypothesis; we cannot determine if the training makes a difference.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck


