Deck 7: Portfolio Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/65
Play
Full screen (f)
Deck 7: Portfolio Theory
1
Which of the following statements regarding portfolio risk and number of stocks is generally true?
A) Adding more stocks increases risk.
B) Adding more stocks decreases risk but does not eliminate it.
C) Adding more stocks has no effect on risk.
D) Adding more stocks decreases only systematic risk.
A) Adding more stocks increases risk.
B) Adding more stocks decreases risk but does not eliminate it.
C) Adding more stocks has no effect on risk.
D) Adding more stocks decreases only systematic risk.
B
2
Which of the following statements about the correlation coefficient of the returns for two securities is not true?
A) It is a statistical measure.
B) It measures the relationship between the two securities' returns.
C) It determines the cause of the relationship between the two securities' returns.
D) Its value falls between -1 and +1.
A) It is a statistical measure.
B) It measures the relationship between the two securities' returns.
C) It determines the cause of the relationship between the two securities' returns.
D) Its value falls between -1 and +1.
C
3
The expected value is the:
A) inverse of the standard deviation.
B) correlation between a security's risk and return.
C) weighted average of all possible outcomes.
D) same as the discrete probability distribution.
A) inverse of the standard deviation.
B) correlation between a security's risk and return.
C) weighted average of all possible outcomes.
D) same as the discrete probability distribution.
C
4
Which of the following involves the interrelationship between security returns as well as the expected returns and variances of those returns?
A) Random diversification
B) Correlating diversification
C) Friedman diversification
D) Markowitz diversification
A) Random diversification
B) Correlating diversification
C) Friedman diversification
D) Markowitz diversification

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
5
In order to determine the expected return of a portfolio, all of the following must be known except:
A) the probabilities of expected returns of the individual assets.
B) the weight of each individual asset in the portfolio.
C) the expected return of each individual asset.
D) the variance of return of each individual asset and correlation of returns between assets.
A) the probabilities of expected returns of the individual assets.
B) the weight of each individual asset in the portfolio.
C) the expected return of each individual asset.
D) the variance of return of each individual asset and correlation of returns between assets.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
6
Company specific risk is also known as:
A) market risk.
B) systematic risk.
C) non-diversifiable risk.
D) diversifiable risk.
A) market risk.
B) systematic risk.
C) non-diversifiable risk.
D) diversifiable risk.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following portfolios has the least reduction of risk?
A) A portfolio with securities all having positive correlation with each other.
B) A portfolio with securities all having zero correlation with each other.
C) A portfolio with securities all having negative correlation with each other.
D) A portfolio with securities all having skewed correlation with each other.
A) A portfolio with securities all having positive correlation with each other.
B) A portfolio with securities all having zero correlation with each other.
C) A portfolio with securities all having negative correlation with each other.
D) A portfolio with securities all having skewed correlation with each other.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is true regarding the expected return of a portfolio?
A) It is a weighted average only for stock portfolios.
B) It can only be positive.
C) It can never be above the highest individual asset return.
D) It is always below the highest individual asset return.
A) It is a weighted average only for stock portfolios.
B) It can only be positive.
C) It can never be above the highest individual asset return.
D) It is always below the highest individual asset return.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
9
Given the following probability distribution, calculate the expected return of security XYZ.
A)16 percent
B)22 percent
C)25 percent
D)18 percent
A)16 percent
B)22 percent
C)25 percent
D)18 percent

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
10
With a continuous probability distribution:
A) a probability is assigned to each possible outcome.
B) possible outcomes are constantly changing.
C) an infinite number of possible outcomes exist.
D) there is no variance.
A) a probability is assigned to each possible outcome.
B) possible outcomes are constantly changing.
C) an infinite number of possible outcomes exist.
D) there is no variance.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
11
Two stocks with perfect negative correlation will have a correlation coefficient of:
A) +1.0
B) -2.0
C) 0.0
D) -1.0
A) +1.0
B) -2.0
C) 0.0
D) -1.0

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following would be considered a random variable?
A) Expected value
B) Correlation coefficient between two assets
C) One-period rate of return for an asset
D) Beta
A) Expected value
B) Correlation coefficient between two assets
C) One-period rate of return for an asset
D) Beta

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following statements regarding expected return of a portfolio is true? It can:
A) be higher than the weighted average expected return of the individual assets.
B) be lower than the weighted average return of the individual assets.
C) never differ from the weighted average expected return of the individual assets.
D) be higher than the expected return of the highest expected return individual asset.
A) be higher than the weighted average expected return of the individual assets.
B) be lower than the weighted average return of the individual assets.
C) never differ from the weighted average expected return of the individual assets.
D) be higher than the expected return of the highest expected return individual asset.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
14
Probability distributions:
A) are always discrete.
B) are always continuous.
C) can be either discrete or continuous.
D) are always symmetric.
A) are always discrete.
B) are always continuous.
C) can be either discrete or continuous.
D) are always symmetric.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
15
Security A and Security B have a correlation coefficient of 0. If Security A's return is expected to increase by 10 percent, Security B's:
A) return should also increase by 10 percent.
B) return should decrease by 10 percent.
C) return should be zero.
D) expected return is impossible to determine from the above information.
A) return should also increase by 10 percent.
B) return should decrease by 10 percent.
C) return should be zero.
D) expected return is impossible to determine from the above information.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
16
The major difference between the correlation coefficient and the covariance is that the correlation coefficient:
A) can be positive, negative, or zero, whereas the covariance is always positive.
B) measures the relationship between securities, whereas the covariance measures the relationship between a security and the market.
C) is a relative measure showing association between security returns, whereas the covariance is an absolute measure showing association between security returns.
D) is a geometric measure, and the covariance is an arithmetic measure.
A) can be positive, negative, or zero, whereas the covariance is always positive.
B) measures the relationship between securities, whereas the covariance measures the relationship between a security and the market.
C) is a relative measure showing association between security returns, whereas the covariance is an absolute measure showing association between security returns.
D) is a geometric measure, and the covariance is an arithmetic measure.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
17
The relevant risk for a well-diversified portfolio is:
A) interest rate risk.
B) inflation risk.
C) business risk.
D) market risk.
A) interest rate risk.
B) inflation risk.
C) business risk.
D) market risk.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is true regarding random diversification?
A) Investment characteristics are considered important in random diversification.
B) Its net benefit eventually disappears as more securities are added.
C) If done correctly, it can eliminate all risk in a portfolio.
D) It eventually removes all company specific risk from a portfolio.
A) Investment characteristics are considered important in random diversification.
B) Its net benefit eventually disappears as more securities are added.
C) If done correctly, it can eliminate all risk in a portfolio.
D) It eventually removes all company specific risk from a portfolio.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
19
The bell-shaped curve, or normal distribution, is considered:
A) discrete.
B) downward sloping.
C) linear.
D) continuous.
A) discrete.
B) downward sloping.
C) linear.
D) continuous.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
20
Each individual asset's weight in the portfolio is found by:
A) dividing the asset's standard deviation by its expected value.
B) calculating the percentage of the asset's value to the total portfolio value.
C) calculating the return of the asset as a percent of total portfolio return.
D) dividing the asset's expected value by its standard deviation.
A) dividing the asset's standard deviation by its expected value.
B) calculating the percentage of the asset's value to the total portfolio value.
C) calculating the return of the asset as a percent of total portfolio return.
D) dividing the asset's expected value by its standard deviation.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
21
When returns are perfectly positively correlated, the risk of the portfolio is:
A) zero.
B) the weighted average of the individual security's risk.
C) equal to the correlation coefficient between the securities.
D) infinite.
A) zero.
B) the weighted average of the individual security's risk.
C) equal to the correlation coefficient between the securities.
D) infinite.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
22
With a discrete probability distribution:
A) a probability is assigned to each possible outcome.
B) possible outcomes are constantly changing.
C) an infinite number of possible outcomes exist.
D) there is no variance.
A) a probability is assigned to each possible outcome.
B) possible outcomes are constantly changing.
C) an infinite number of possible outcomes exist.
D) there is no variance.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
23
Markowitz's main contribution to portfolio theory is that risk is:
A) the same for each type of financial asset.
B) a function of credit, liquidity, and market factors.
C) not quantifiable.
D) influenced more by covariance than variance when portfolios are large.
A) the same for each type of financial asset.
B) a function of credit, liquidity, and market factors.
C) not quantifiable.
D) influenced more by covariance than variance when portfolios are large.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
24
When the covariance is positive, the correlation will be:
A) positive.
B) negative.
C) zero.
D) impossible to determine.
A) positive.
B) negative.
C) zero.
D) impossible to determine.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
25
Owning two securities instead of one will not improve a portfolio's risk-return tradeoff if the two securities are:
A) perfectly positively correlated with each other.
B) perfectly independent of each other.
C) perfectly negatively correlated with each other.
D) of the same category,
E)g. blue chips.
A) perfectly positively correlated with each other.
B) perfectly independent of each other.
C) perfectly negatively correlated with each other.
D) of the same category,
E)g. blue chips.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
26
In a portfolio containing 10 securities, the number of unique correlations is:
A) 10.
B) 45.
C) 90.
D) 100.
A) 10.
B) 45.
C) 90.
D) 100.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
27
According to the Law of Large Numbers, the larger the sample size, the more likely it is that the sample mean will be close to the population expected value.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
28
A negative correlation coefficient indicates that the returns of two securities have a tendency to move in opposite directions.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
29
Standard deviations for well-diversified portfolios are reasonably steady over time.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
30
Calculate the risk (standard deviation) of the following two-security portfolio if the correlation coefficient between the two securities is equal to 0.5.
A) 17.0 percent
B) 5.4 percent
C) 2.0 percent
D) 3.7 percent
A) 17.0 percent
B) 5.4 percent
C) 2.0 percent
D) 3.7 percent

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
31
Walter has his entire portfolio invested in the stock of the company where he works. He is considering purchasing one of four ETFs, each of which has the same expected return, but has a different correlation with his portfolio. Walter should choose the ETF that has a correlation of:
A) -0.3.
B) 0.0.
C) 0.5.
D) 1.0.
A) -0.3.
B) 0.0.
C) 0.5.
D) 1.0.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
32
Portfolio risk is most often measured by professional investors using the:
A) expected value.
B) portfolio's beta.
C) weighted average of the individual asset's risk.
D) portfolio's standard deviation.
A) expected value.
B) portfolio's beta.
C) weighted average of the individual asset's risk.
D) portfolio's standard deviation.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
33
The optimal portfolio for an investor is the one that offers:
A) the highest expected return.
B) the lowest risk.
C) the lowest transactions costs.
D) the highest return per unit of risk.
A) the highest expected return.
B) the lowest risk.
C) the lowest transactions costs.
D) the highest return per unit of risk.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
34
Portfolio risk is a weighted average of the individual security risks.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
35
The major problem with the Markowitz model is its:
A) lack of accuracy.
B) predictability flaws.
C) complexity.
D) inability to handle large number of inputs.
A) lack of accuracy.
B) predictability flaws.
C) complexity.
D) inability to handle large number of inputs.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
36
Randomly adding securities to a portfolio will most likely:
A) reduce its risk and increase its expected return.
B) reduce its risk and decrease its expected return.
C) increase its risk and increase its expected return.
D) reduce its risk and keep its expected return unchanged.
A) reduce its risk and increase its expected return.
B) reduce its risk and decrease its expected return.
C) increase its risk and increase its expected return.
D) reduce its risk and keep its expected return unchanged.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
37
A probability distribution shows the likely outcomes that may occur and the probabilities associated with these likely outcomes.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
38
The average correlation of stocks in the S&P 500 with the Index itself is closest to:
A) 0.0.
B) 0.3.
C) 0.5.
D) 0.8.
A) 0.0.
B) 0.3.
C) 0.5.
D) 0.8.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
39
A change in the correlation coefficient of the returns of two securities in a portfolio causes a change in:
A) both the expected return and the risk of the portfolio.
B) only the expected return of the portfolio.
C) only the risk level of the portfolio.
D) neither the expected return nor the risk level of the portfolio.
A) both the expected return and the risk of the portfolio.
B) only the expected return of the portfolio.
C) only the risk level of the portfolio.
D) neither the expected return nor the risk level of the portfolio.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
40
Investments in commodities such as precious metals may provide additional
diversification opportunities for portfolios consisting of stocks and bonds.
diversification opportunities for portfolios consisting of stocks and bonds.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
41
In a portfolio consisting of two perfectly negatively correlated securities, the highest attainable expected return will consist of a portfolio containing 100% of the asset with the highest expected return.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
42
In the case of a four-security portfolio, there will be 8 covariances.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
43
How risky is it to investment in a limited liability company (LLC) that searches for sunken treasure?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
44
If security A has a correlation of 0.5 with security B, it indicates that security A causes half of the movement in security B.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
45
Why was the Markowitz model impractical for commercial use when it was first introduced in 1952? What has changed since then?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
46
A portfolio consisting of two securities with perfect negative correlation in the proper proportions can be shown to have a standard deviation of zero. What makes this riskless portfolio impossible to achieve in the real world?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
47
Throwing a dart at the Wall Street Journal and selecting stocks on this basis would be considered random diversification.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
48
Provide an example of two industries that might have low correlation with one another. Give an example that might exhibit high correlation.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
49
The correlation coefficient identifies what causes the relative movement in returns between two securities.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
50
Are the expected return and standard deviation of a portfolio both weighted averages of the individual security's expected returns and standard deviations? If not, what other factors are required?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
51
How is the correlation coefficient important in choosing among securities for a portfolio?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
52
When constructing a portfolio, standard deviations, expected returns, and correlation coefficients are typically calculated from historical data. Why may that be a problem?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
53
If an analyst uses ex post data to calculate the correlation coefficient and covariance and uses them in the Markowitz model, the assumption is that past relationships will continue in the future.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
54
An investor combines two securities with perfect negative correlation and achieves a portfolio risk of zero. Will the portfolio also have an expected return of zero?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
55
Is it possible for a portfolio to have an expected return and risk that falls outside the range of expected returns and risks of the securities included in the portfolio?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
56
Conventional wisdom has long held that diversification of a stock portfolio should be across industries. Does the correlation coefficient indirectly recommend the same thing?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
57
Is it wise for individuals to invest a portion of their investment portfolio in the common stock of the firm where they are employed? Explain why or why not.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
58
Why is it more difficult to put Markowitz diversification into effect than random diversification?

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
59
Portfolio risk can be reduced by reducing portfolio weights for assets with relatively high positive correlations.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
60
Combining two securities with perfect negative correlation will always reduce risk to 0.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
61
An investor has her $1 million portfolio invested in two different mutual funds as follows: $400,000 in a small-cap fund and $600,000 in a balanced fund. The small-cap fund has an expected return of 12% and a variance of 625, whereas the balanced fund has an expected return of 7% and a variance of 81. The covariance between the two funds is 122.
A. Find the investor's expected portfolio return.
A. Find the investor's expected portfolio return.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
62
Given the following information, Calculate the expected return and risk (standard deviation) for General Fudge.
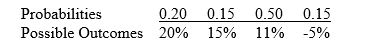
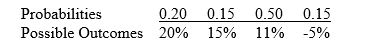

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
63
* Use the following information to solve the next two problems *

Find the expected return for a portfolio that is 70% invested in the energy ETF and 30% in the technology ETF.

Find the expected return for a portfolio that is 70% invested in the energy ETF and 30% in the technology ETF.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
64
* Use the following information to solve the next two problems *
-Find the standard deviation for a portfolio that is 70% invested in the energy ETF and 30% in the technology ETF.
-Find the standard deviation for a portfolio that is 70% invested in the energy ETF and 30% in the technology ETF.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck
65
An investor has calculated the covariance between a utility ETF and a bank ETF at 124. The variance of the utility ETF is 398 and the variance of the bank ETF is 548. Find the correlation between the two ETFs.

Unlock Deck
Unlock for access to all 65 flashcards in this deck.
Unlock Deck
k this deck


