Deck 5: Network Modeling
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/72
Play
Full screen (f)
Deck 5: Network Modeling
1
How could a network be modified if demand exceeds supply?
A) add extra supply arcs
B) remove the extra demand arcs
C) add a dummy supply
D) add a dummy demand
A) add extra supply arcs
B) remove the extra demand arcs
C) add a dummy supply
D) add a dummy demand
C
2
Decision variables in network flow problems are represented by
A) nodes.
B) arcs.
C) demands.
D) supplies.
A) nodes.
B) arcs.
C) demands.
D) supplies.
B
3
In a transshipment problem, which of the following statements is a correct representation of the balance-of-flow rule if Total Supply < Total Demand?
A) Inflow Outflow Supply or Demand
B) Inflow + Outflow Supply or Demand
C) Inflow Outflow Supply or Demand
D) Inflow + Outflow Supply or Demand
A) Inflow Outflow Supply or Demand
B) Inflow + Outflow Supply or Demand
C) Inflow Outflow Supply or Demand
D) Inflow + Outflow Supply or Demand
Inflow Outflow Supply or Demand
4
The street intersections in a city road network represent
A) nodes.
B) arcs.
C) resources.
D) expenses.
A) nodes.
B) arcs.
C) resources.
D) expenses.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
5
The number of constraints in network flow problems is determined by the number of
A) nodes.
B) arcs.
C) demands.
D) supplies.
A) nodes.
B) arcs.
C) demands.
D) supplies.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
6
The constraint X13 + X23-X34 50 indicates that
A) 50 units are required at node 3.
B) 50 units will be shipped from node 3.
C) 50 units will be shipped in from node 1.
D) 50 units must pass through node 3.
A) 50 units are required at node 3.
B) 50 units will be shipped from node 3.
C) 50 units will be shipped in from node 1.
D) 50 units must pass through node 3.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
7
Supply quantities for supply nodes in a transshipment problem are customarily indicated by
A) positive numbers.
B) negative numbers.
C) imaginary numbers.
D) either positive or negative numbers.
A) positive numbers.
B) negative numbers.
C) imaginary numbers.
D) either positive or negative numbers.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
8
Demand quantities for demand nodes in a transshipment problem are customarily indicated by
A) positive numbers.
B) negative numbers.
C) imaginary numbers.
D) either positive or negative numbers.
A) positive numbers.
B) negative numbers.
C) imaginary numbers.
D) either positive or negative numbers.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
9
Almost all network problems can be viewed as special cases of the
A) transshipment problem.
B) shortest path problem.
C) maximal flow problem.
D) minimal spanning tree problem.
A) transshipment problem.
B) shortest path problem.
C) maximal flow problem.
D) minimal spanning tree problem.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
10
A factory which ships items through the network would be represented by which type of node?
A) demand
B) supply
C) random
D) decision
A) demand
B) supply
C) random
D) decision

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
11
What is the correct constraint for node 2 in the following diagram? 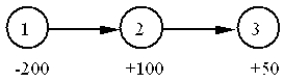
A) X12 + X23 = 100
B) X12 -X23 100
C) -X12 + X23 -100
D) X12 -X23 100

A) X12 + X23 = 100
B) X12 -X23 100
C) -X12 + X23 -100
D) X12 -X23 100

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
12
What is the interpretation of units "shipped" along arcs from dummy supply nodes to demand nodes?
A) Indicates unmet demand at demand nodes
B) Indicates unmet supply at demand nodes
C) Indicates unmet demand at supply nodes
D) Indicates unmet supply at supply nodes
A) Indicates unmet demand at demand nodes
B) Indicates unmet supply at demand nodes
C) Indicates unmet demand at supply nodes
D) Indicates unmet supply at supply nodes

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
13
How many constraints are there in a transshipment problem which has n nodes and m arcs?
A) n
B) m
C) n + m
D) m - n
A) n
B) m
C) n + m
D) m - n

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
14
Which balance of flow rule should be applied at each node in a network flow problem when Total Supply > Total Demand?
A) Inflow - Outflow Supply or Demand
B) Inflow- Outflow Supply or Demand
C) Inflow - Outflow = Supply or Demand
D) Inflow- Supply Outflow or Demand
A) Inflow - Outflow Supply or Demand
B) Inflow- Outflow Supply or Demand
C) Inflow - Outflow = Supply or Demand
D) Inflow- Supply Outflow or Demand

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
15
What formula would be entered in cell G18 in this Excel model? 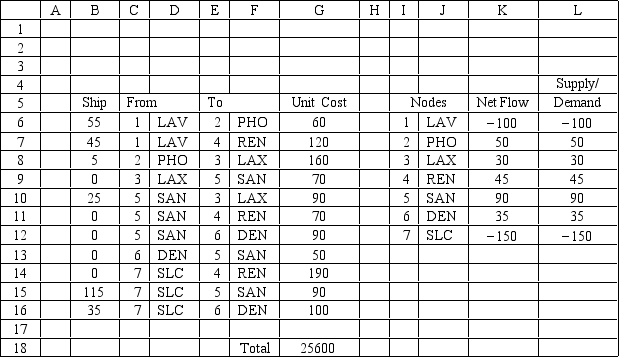
A) SUMPRODUCT(K6:K12,L6:L12)
B) SUMPRODUCT(B6:B16,G6:G16)
C) SUMPRODUCT(G6:G16,K6:K12)
D) SUMPRODUCT(B6:G16,L6:L12)

A) SUMPRODUCT(K6:K12,L6:L12)
B) SUMPRODUCT(B6:B16,G6:G16)
C) SUMPRODUCT(G6:G16,K6:K12)
D) SUMPRODUCT(B6:G16,L6:L12)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
16
The right hand side value for the ending node in a shortest path problem has a value of
A) -1
B) 0
C) 1
D) 2
A) -1
B) 0
C) 1
D) 2

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the equipment replacement problem presented in the chapter. Recall that in the network model formulation of this problem a node represents a year when the equipment was purchased. An arc from node i to node j indicates that the equipment purchased in year i can be replaced at the beginning of year j. How could the network model below be modified to depict an equipment purchase in year 4 and operating costs only through the remainder of the planning window? 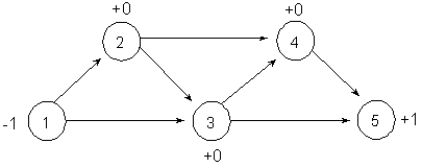
A) Modify the cost on arc 4-5 to account for only operating costs.
B) Add a second arc 4-5 to represent just the operating costs.
C) Add a dummy node, 6, so that arc 4-6 represents just the operating costs.
D) Add a dummy node, 6, so that arc 4-5 represents operating costs and 5-6 represents new equipment purchase.

A) Modify the cost on arc 4-5 to account for only operating costs.
B) Add a second arc 4-5 to represent just the operating costs.
C) Add a dummy node, 6, so that arc 4-6 represents just the operating costs.
D) Add a dummy node, 6, so that arc 4-5 represents operating costs and 5-6 represents new equipment purchase.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
18
The arcs in a network indicate all of the following except?
A) routes
B) paths
C) constraints
D) connections
A) routes
B) paths
C) constraints
D) connections

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
19
A node which can both send to and receive from other nodes is a
A) demand node.
B) supply node.
C) random node.
D) transshipment node.
A) demand node.
B) supply node.
C) random node.
D) transshipment node.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
20
The right hand side value for the starting node in a shortest path problem has a value of
A) -1
B) 0
C) 1
D) 2
A) -1
B) 0
C) 1
D) 2

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
21
What is missing from transportation problems compared to transshipment problems?
A) arcs
B) demand nodes
C) transshipment nodes
D) supply nodes
A) arcs
B) demand nodes
C) transshipment nodes
D) supply nodes

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
22
Which property of network flow models guarantees integer solutions?
A) linear constraints and balance of flow equation format
B) linear objective function coefficients
C) integer objective function coefficients
D) integer constraint RHS values and balance of flow equation format
A) linear constraints and balance of flow equation format
B) linear objective function coefficients
C) integer objective function coefficients
D) integer constraint RHS values and balance of flow equation format

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
23
If a side constraint for a network flow model cannot be avoided, and non-integer solutions result, how can the solution be expressed as an integer solution?
A) Force all the arc flow decision variables to be integer.
B) Round off all the non-integer arc flow decision variables.
C) Increase the supply until the solutions are all integer using a dummy supply node.
D) Increase the demand until the solutions are all integer using a dummy demand node.
A) Force all the arc flow decision variables to be integer.
B) Round off all the non-integer arc flow decision variables.
C) Increase the supply until the solutions are all integer using a dummy supply node.
D) Increase the demand until the solutions are all integer using a dummy demand node.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
24
What is the constraint for node 2 in the following shortest path problem? 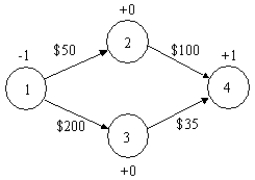
A) -X12 -X13 = 0
B) -X12-X24 = 1
C) X12 + X13 = 0
D) -X12 + X24 = 0

A) -X12 -X13 = 0
B) -X12-X24 = 1
C) X12 + X13 = 0
D) -X12 + X24 = 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
25
Which method is preferred for solving minimal spanning tree problems?
A) linear programming
B) transshipment models
C) simulation
D) manual algorithms
A) linear programming
B) transshipment models
C) simulation
D) manual algorithms

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
26
What happens to the solution of a network flow model if side constraints are added that do not obey the balance of flow rules?
A) The model solution is not guaranteed to be integer.
B) The model solution will more accurately reflect reality.
C) The model solution will be integer but more accurate.
D) The model solution is not guaranteed to be feasible.
A) The model solution is not guaranteed to be integer.
B) The model solution will more accurately reflect reality.
C) The model solution will be integer but more accurate.
D) The model solution is not guaranteed to be feasible.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
27
What is the objective function in the following maximal flow problem? 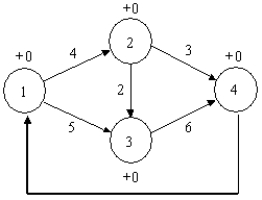
A) MIN X41
B) MAX X12 + X13
C) MAX X14
D) MAX X41

A) MIN X41
B) MAX X12 + X13
C) MAX X14
D) MAX X41

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
28
When might a network flow model for a transportation/assignment problem be preferable to a matrix form for the problem?
A) When an integer solution is required.
B) When the problem is large and not fully connected.
C) When the problem is large and fully connected.
D) When supply exceeds demand.
A) When an integer solution is required.
B) When the problem is large and not fully connected.
C) When the problem is large and fully connected.
D) When supply exceeds demand.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
29
What is the constraint for node 2 in the following maximal flow problem? 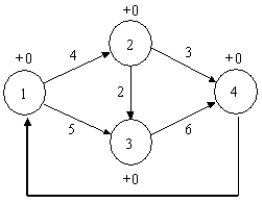
A) X12 -X23 - X24 = 0
B) X12 + X23 + X24 = 0
C) X12 - 4
D) X12 + X13 -X23 = 0

A) X12 -X23 - X24 = 0
B) X12 + X23 + X24 = 0
C) X12 - 4
D) X12 + X13 -X23 = 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
30
The equipment replacement problem is an example of which network problem?
A) transportation problem.
B) shortest path problem.
C) maximal flow problem.
D) minimal spanning tree problem.
A) transportation problem.
B) shortest path problem.
C) maximal flow problem.
D) minimal spanning tree problem.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
31
A maximal flow problem differs from other network models in which way?
A) arcs are two directional
B) multiple supply nodes are used
C) arcs have limited capacity
D) arcs have unlimited capacity
A) arcs are two directional
B) multiple supply nodes are used
C) arcs have limited capacity
D) arcs have unlimited capacity

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
32
In generalized network flow problems
A) solutions may not be integer values.
B) flows along arcs may increase or decrease.
C) it can be difficult to tell if total supply is adequate to meet total demand.
D) all of these.
A) solutions may not be integer values.
B) flows along arcs may increase or decrease.
C) it can be difficult to tell if total supply is adequate to meet total demand.
D) all of these.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
33
What is the objective function for the following shortest path problem? 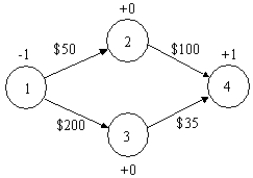
A) -X12 - X13 = 0
B) MIN -50 X12-200 X13 + 100 X24 + 35 X34
C) MIN 50 X12 + 200 X13 + 100 X24 + 35 X34
D) MAX -50 X12 - 200 X13 + 100 X24 + 35 X34

A) -X12 - X13 = 0
B) MIN -50 X12-200 X13 + 100 X24 + 35 X34
C) MIN 50 X12 + 200 X13 + 100 X24 + 35 X34
D) MAX -50 X12 - 200 X13 + 100 X24 + 35 X34

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
34
Which method is preferred for solving fully connected transportation problems?
A) linear programming
B) network flow methods
C) trial and error
D) simulation
A) linear programming
B) network flow methods
C) trial and error
D) simulation

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
35
A network flow problem that allows gains or losses along the arcs is called a
A) non-constant network flow model.
B) non-directional, shortest path model.
C) generalized network flow model.
D) transshipment model with linear side constraints.
A) non-constant network flow model.
B) non-directional, shortest path model.
C) generalized network flow model.
D) transshipment model with linear side constraints.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
36
An oil company wants to create lube oil, gasoline and diesel fuel at two refineries. There are two sources of crude oil. Consider arc 2-4. The per unit shipping cost of crude B from source 2 (node 2) to refinery 2 (node 4) is $11 and the yield is 85 percent. The following flowchart depicts this problem. What is the balance of flow constraint for node 7 (Diesel)? 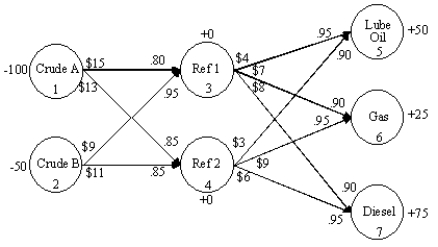
A) X35 + X36 + X37 = 75
B) X37 + X47 75
C) .90 X37 + .95 X47 = 75
D) X37 + X47 -X36 -X35 - X45 -X46 75

A) X35 + X36 + X37 = 75
B) X37 + X47 75
C) .90 X37 + .95 X47 = 75
D) X37 + X47 -X36 -X35 - X45 -X46 75

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
37
Maximal flow problems are converted to transshipment problems by
A) connecting the supply and demand nodes with a return arc
B) adding extra supply nodes
C) adding supply limits on the supply nodes
D) requiring integer solutions
A) connecting the supply and demand nodes with a return arc
B) adding extra supply nodes
C) adding supply limits on the supply nodes
D) requiring integer solutions

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
38
Consider modeling a warehouse with three in-flow arcs and three outflow arcs. The warehouse node is a transshipment node but has a capacity of 100. How would one modify the network model to avoid adding a side constraint that limits either the sum of in-flows or the sum of the out-flows to 100?
A) Place a limit of 34 on each in-flow arc.
B) Add a side constraint limiting the out-flow arcs sum to 100.
C) Separate the warehouse node into two nodes, connected by a single arc, with capacity of 100.
D) It cannot be accomplished, a side constraint must be added.
A) Place a limit of 34 on each in-flow arc.
B) Add a side constraint limiting the out-flow arcs sum to 100.
C) Separate the warehouse node into two nodes, connected by a single arc, with capacity of 100.
D) It cannot be accomplished, a side constraint must be added.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
39
An oil company wants to create lube oil, gasoline and diesel fuel at two refineries. There are two sources of crude oil. Consider arc 2-4. The per unit shipping cost of crude B from source 2 (node 2) to refinery 2 (node 4) is $11 and the yield is 85 percent. The following network representation depicts this problem. What is the balance of flow constraint for node 3 (Refinery 1)? 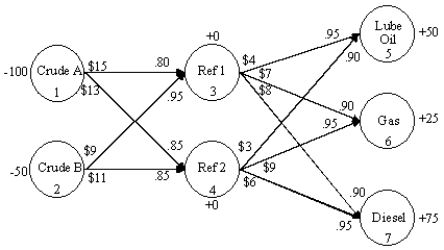
A) X13 + X23 - .95 X35 - .90 X36 - .90 X37 = 0
B) .80 X13 + .95 X23-X35 -X36-X37 = 0
C) .80 X13 + .95 X23 - .90 X36 - .90 X37 0
D) X13 + X23 -X35 - X36 - X37 0

A) X13 + X23 - .95 X35 - .90 X36 - .90 X37 = 0
B) .80 X13 + .95 X23-X35 -X36-X37 = 0
C) .80 X13 + .95 X23 - .90 X36 - .90 X37 0
D) X13 + X23 -X35 - X36 - X37 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
40
Which formula should be used to determine the Net Flow values in cell K6 in the following spreadsheet model? 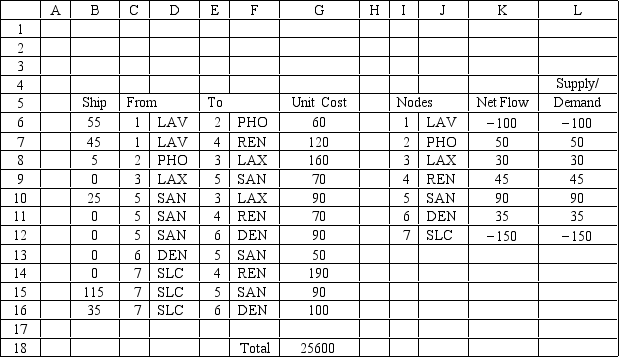
A) SUMIF($C$6:$C$16,I6,$B$6:$B$16)-SUMIF($E$6:$E$16,I6,$B$6:$B$16)
B) SUMIF($I$6:$I$12,B6,$B$6:$B$16)-SUMIF($I$6:$I$12,I6,$B$6:$B$16)
C) SUMIF($E$6:$E$16,I6,$B$6:$B$16)-SUMIF($C$6:$C$16,I6,$B$6:$B$16)
D) SUMPRODUCT(B6:B16,G6:G16)

A) SUMIF($C$6:$C$16,I6,$B$6:$B$16)-SUMIF($E$6:$E$16,I6,$B$6:$B$16)
B) SUMIF($I$6:$I$12,B6,$B$6:$B$16)-SUMIF($I$6:$I$12,I6,$B$6:$B$16)
C) SUMIF($E$6:$E$16,I6,$B$6:$B$16)-SUMIF($C$6:$C$16,I6,$B$6:$B$16)
D) SUMPRODUCT(B6:B16,G6:G16)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
41
An oil company wants to create lube oil, gasoline and diesel fuel at two refineries. There are two sources of crude oil. The following Excel spreadsheet shows this problem. What formula should be entered in cell E6 (and copied to cells E7:E15) in this spreadsheet?
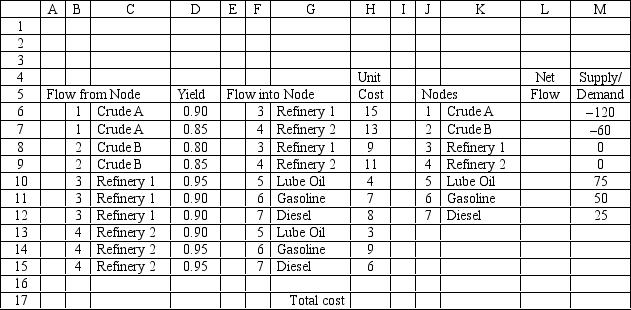


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
42
An oil company wants to create lube oil, gasoline and diesel fuel at two refineries. There are two sources of crude oil. The following Excel spreadsheet shows this problem.
What values would you enter in the Risk Solver Platform (RSP) task pane for the following Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:
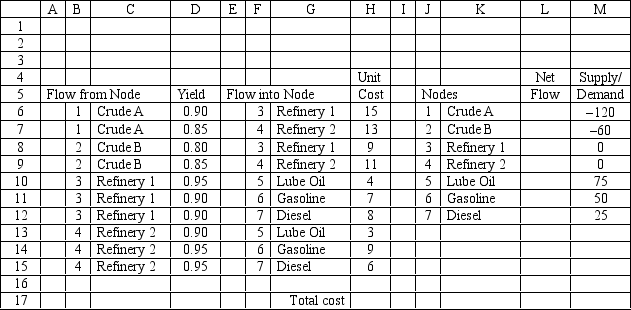
What values would you enter in the Risk Solver Platform (RSP) task pane for the following Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
43
A company needs to ship 100 units from Seattle to Denver at the lowest possible cost. The costs associated with shipping between the cities are:
 What values should go into cells G6:L13 in the following Excel spreadsheet?
What values should go into cells G6:L13 in the following Excel spreadsheet?
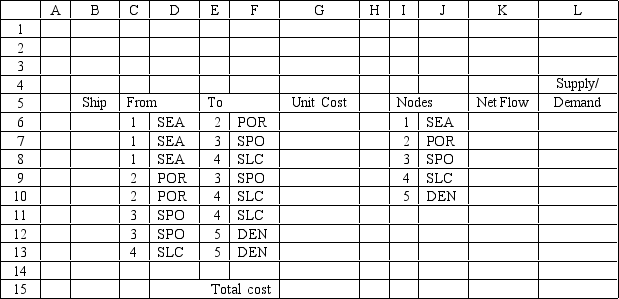
 What values should go into cells G6:L13 in the following Excel spreadsheet?
What values should go into cells G6:L13 in the following Excel spreadsheet?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
44
Draw the network representation of the following network flow problem.
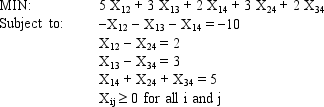
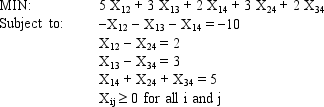

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
45
The following network depicts an assignment/transportation problem for Joe Fix's repair scheduling problem. Formulate the LP for Joe assuming he wishes to maximize the total repairperson to plane assignment preferences.
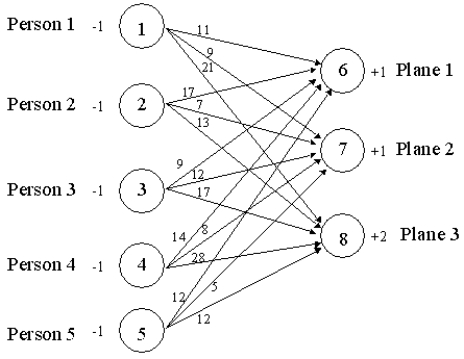


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
46
Joe Fix plans the repair schedules each day for the Freeway Airline. Joe has 3 planes in need of repair and 5 repair personnel at his disposal. Each plane requires a single repairperson, except plane 3, which needs 2 personnel. Anyone not assigned to maintaining an airplane works in the maintenance shop for the day (not modeled). Each repairperson has different likes and dislikes regarding the types of repairs they prefer. For each plane, Joe has pulled the expected maintenance and determined the total preference matrix for his repair personnel. The preference matrix is:
 Draw the balanced network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
Draw the balanced network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
 Draw the balanced network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
Draw the balanced network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
47
The following network depicts a balanced transportation/distribution problem for Clifton Distributing. Formulate the LP for Clifton assuming they wish to minimize the total product-miles incurred.
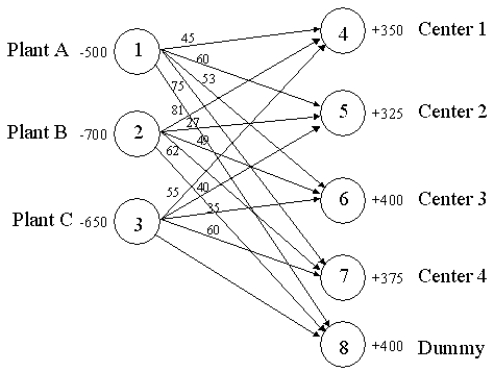


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
48
A company wants to determine the optimal replacement policy for its photocopier. The company does not keep photocopiers longer than 4 years. The company has estimated the annual costs for photocopiers during each of the 4 years and developed the following network representation of the problem.
Write out the LP formulation for this problem.
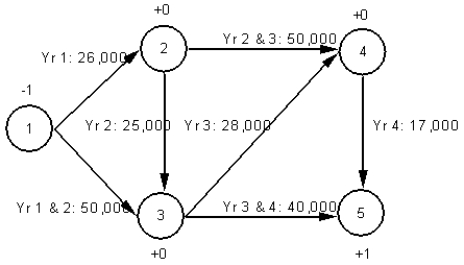
Write out the LP formulation for this problem.


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
49
Clifton Distributing has three plants and four distribution centers. The plants, their supply, the distribution centers, their demands, and the distance between each location is summarized in the following table:
 Draw the balanced transportation network for Clifton's distribution problem.
Draw the balanced transportation network for Clifton's distribution problem.
 Draw the balanced transportation network for Clifton's distribution problem.
Draw the balanced transportation network for Clifton's distribution problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
50
An oil company wants to create lube oil, gasoline and diesel fuel at two refineries. There are two sources of crude oil. The following network representation depicts this problem.
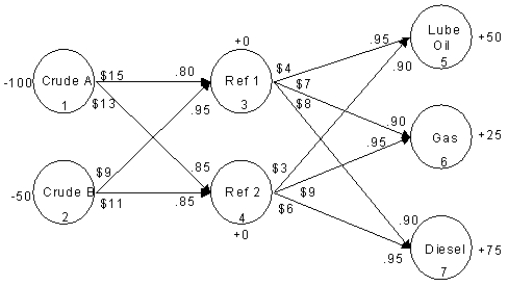 Write out the LP formulation for this problem.
Write out the LP formulation for this problem.
 Write out the LP formulation for this problem.
Write out the LP formulation for this problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
51
A company needs to ship 100 units from Seattle to Denver at the lowest possible cost. The costs associated with shipping between the cities are listed below. Also, the decision variable associated with each pair of cities is shown next to the cost.
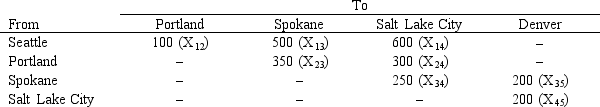 Write out the LP formulation for this problem.
Write out the LP formulation for this problem.
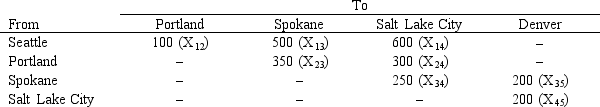 Write out the LP formulation for this problem.
Write out the LP formulation for this problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
52
A company needs to ship 100 units from Seattle to Denver at the lowest possible cost. The costs associated with shipping between the cities are:
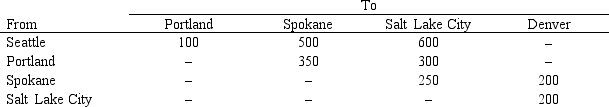 What values would you enter in the Risk Solver Platform (RSP) task pane for the following Excel spreadsheet?
What values would you enter in the Risk Solver Platform (RSP) task pane for the following Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:
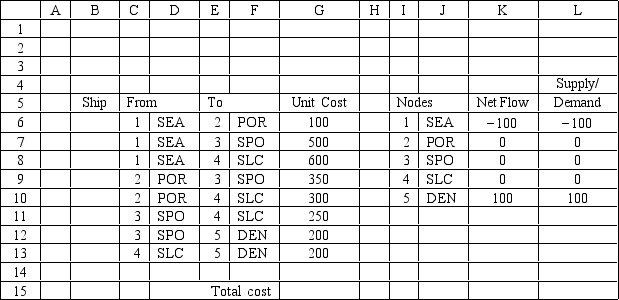
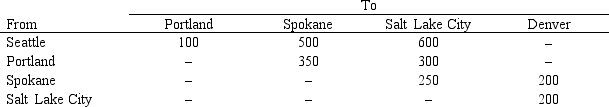 What values would you enter in the Risk Solver Platform (RSP) task pane for the following Excel spreadsheet?
What values would you enter in the Risk Solver Platform (RSP) task pane for the following Excel spreadsheet?Objective Cell:
Variables Cells:
Constraints Cells:


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
53
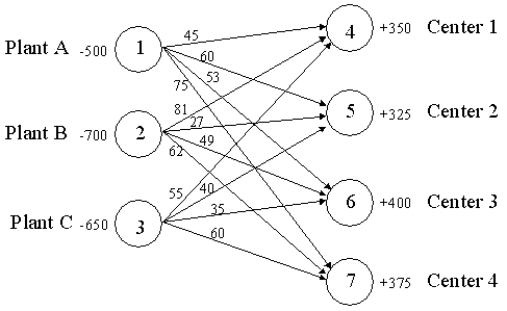
The following network depicts a transportation/distribution problem for Clifton Distributing. Formulate the LP for Clifton assuming they wish to minimize the total product-miles incurred.


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
54
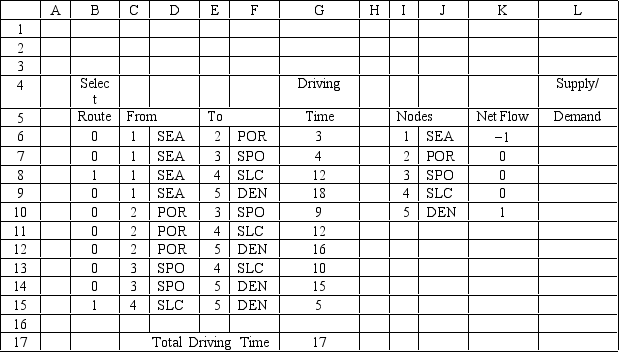
A trucking company wants to find the quickest route from Seattle to Denver. What values should be placed in cells L6:L10 of the following Excel spreadsheet?


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
55
A company wants to determine the optimal replacement policy for its delivery truck. New trucks cost $30,000. The company does not keep trucks longer than 2 years and has estimated the annual operating costs and trade-in values for trucks during each of the 2 years as:
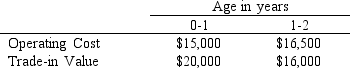 Draw the network representation of this problem.
Draw the network representation of this problem.
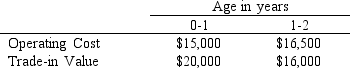 Draw the network representation of this problem.
Draw the network representation of this problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
56
Clifton Distributing has three plants and four distribution centers. The plants, their supply, the distribution centers, their demands, and the distance between each location is summarized in the following table:
 Draw the transportation network for Clifton's distribution problem.
Draw the transportation network for Clifton's distribution problem.
 Draw the transportation network for Clifton's distribution problem.
Draw the transportation network for Clifton's distribution problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
57
How many arcs are required to make a spanning tree in a network with n nodes and m arcs?
A) n
B) n - 1
C) m
D) m- 1
A) n
B) n - 1
C) m
D) m- 1

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
58
The minimal spanning tree solution algorithm works by defining a subnetwork and
A) adding the least expensive arc which connects any node in the current subnetwork to any node not in the current subnetwork.
B) adding the most expensive arc which connects any node in the current subnetwork to any node not in the current subnetwork.
C) adding the least expensive arc which connects unconnected nodes in the current subnetwork.
D) adding the least expensive arc which connects the most recently added node in the current subnetwork to the closest node not in the current subnetwork.
A) adding the least expensive arc which connects any node in the current subnetwork to any node not in the current subnetwork.
B) adding the most expensive arc which connects any node in the current subnetwork to any node not in the current subnetwork.
C) adding the least expensive arc which connects unconnected nodes in the current subnetwork.
D) adding the least expensive arc which connects the most recently added node in the current subnetwork to the closest node not in the current subnetwork.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
59
Joe Fix plans the repair schedules each day for the Freeway Airline. Joe has 3 planes in need of repair and 5 repair personnel at his disposal. Each plane requires a single repairperson, except plane 3, which needs 2 personnel. Anyone not assigned to maintaining an airplane works in the maintenance shop for the day (not modeled). Each repairperson has different likes and dislikes regarding the types of repairs they prefer. For each plane, Joe has pulled the expected maintenance and determined the total preference matrix for his repair personnel. The preference matrix is:
 Draw the network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
Draw the network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
 Draw the network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
Draw the network flow for this assignment problem assuming Joe would like to maximize the total preference in his worker-to-aircraft schedule.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
60
A company needs to ship 100 units from Roanoke to Washington at the lowest possible cost. The costs associated with shipping between the cities are:
 Draw the network representation of this problem.
Draw the network representation of this problem.
 Draw the network representation of this problem.
Draw the network representation of this problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
61
Draw the network and indicate how many units are flowing along each arc based on the following Risk Solver Platform (RSP) solution.
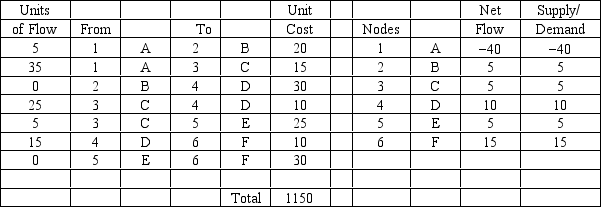


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
62
Draw the network representation of this LP model. What type of problem is it?
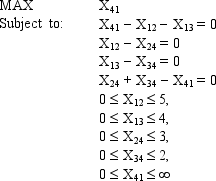
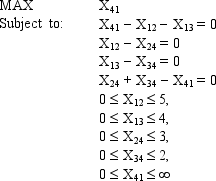

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the following minimal spanning tree problem starting at node 1.
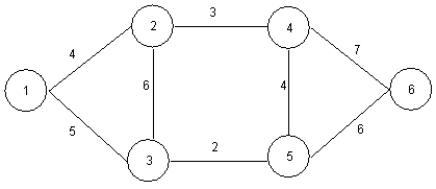


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
64
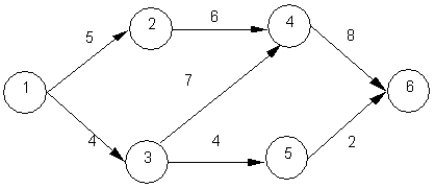
Solve the following minimal spanning tree problem starting at node 1.


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
65
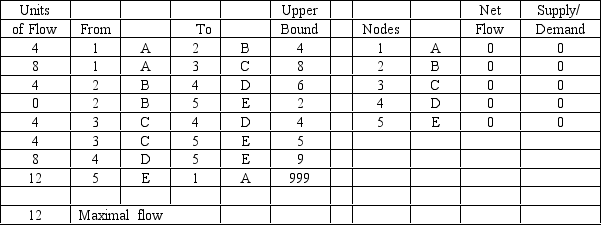
Draw the network and solution for the maximal flow problem represented by the following Excel spreadsheet.


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
66
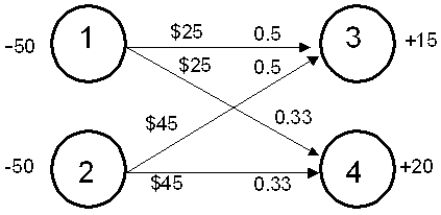
A manufacturing company has a pool of 50 labor hours. A customer has requested two products, Product A and Product B, and has requested 15 and 20 of each respectively. It requires 2 hours of labor to produce Product A and 3 hours of labor to produce Product B. The company can obtain up to 50 additional hours of labor if required. In-house labor costs $25 per hour while contracted labor costs $45 per hour. The following network flow model captures this problem.
 Write out the LP formulation for this problem.
Write out the LP formulation for this problem.
 Write out the LP formulation for this problem.
Write out the LP formulation for this problem.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
67
A manufacturing company has a pool of 50 labor hours. A customer has requested two products, Product A and Product B, and has requested 15 and 20 of each respectively. It requires 2 hours of labor to produce Product A and 3 hours of labor to produce Product B. The company can obtain up to 50 additional hours of labor if required. In-house labor costs $25 per hour while contracted labor costs $45 per hour. Draw the network flow model that captures this problem.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
68
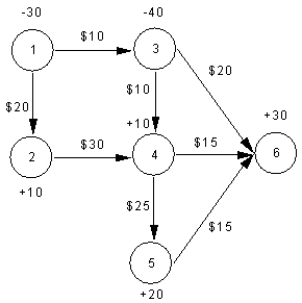
A company wants to manage its distribution network which is depicted below. Identify the supply, demand and transshipment nodes in this problem.


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
69
The following network depicts a balanced assignment/transportation problem for Joe Fix's repair scheduling problem. Formulate the LP for Joe assuming he wishes to maximize the total repairperson to plane assignment preferences.
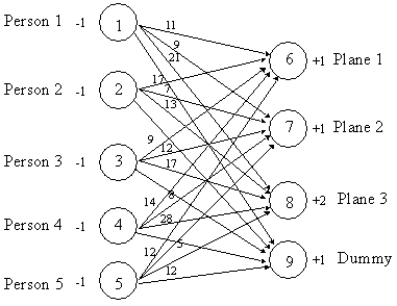


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
70
A railroad needs to move the maximum amount of material through its rail network. Formulate the LP model to determine this maximum amount based on the following network diagram.
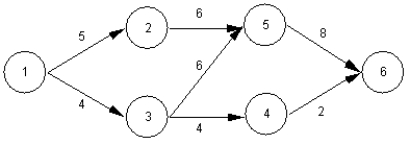


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
71
Project 5.2 - Small Production Planning Project
(Fixed Charge Problem via Network Flow with Side Constraints)
Jack Small Enterprises runs two factories in Ohio, one in Toledo and one in Centerville. His factories produce a variety of products. Two of his product lines are polished wood clocks which he adorns with a regional theme. Naturally, clocks popular in the southwest are not as popular in the northeast, and vice versa. Each plant makes both of the clocks. These clocks are shipped to St Louis for distribution to the southeast and western states and to Pittsburg for distribution to the south and northeast.
Jack is considering streamlining his plants by removing certain production lines from certain plants. Among his options is potentially eliminating the clock production line at either the Toledo or the Centerville plant. Each plant carries a fixed operating cost for setting up the line and a unit production cost, both in terms of money and factory worker hours. This information is summarized in the table below.
 The Southwest clocks are sold for $23 each and the Northwest clocks are sold for $25 each. Demand rates used for production planning are 1875 Southwest clocks for sale out of the St Louis distribution center and 2000 Northeast clocks for sale out of the Pittsburg distribution center. Assume all these units are sold. The per clock transportation costs from plant to distribution center is given in the following table.
The Southwest clocks are sold for $23 each and the Northwest clocks are sold for $25 each. Demand rates used for production planning are 1875 Southwest clocks for sale out of the St Louis distribution center and 2000 Northeast clocks for sale out of the Pittsburg distribution center. Assume all these units are sold. The per clock transportation costs from plant to distribution center is given in the following table.
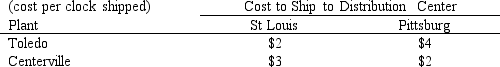 Develop a generalized network flow model for this problem and implement this model in solver. Use the model to answer the following questions.
Develop a generalized network flow model for this problem and implement this model in solver. Use the model to answer the following questions.
a.
Should any of the production lines be shut down?
b.
How should worker hours be allocated to produce the clocks to meet the demand forecasts? Are there any excess hours, and if so how many?
c.
What is the expected monthly profit?
d.
If a plant is closed, what are the estimated monthly savings?
(Fixed Charge Problem via Network Flow with Side Constraints)
Jack Small Enterprises runs two factories in Ohio, one in Toledo and one in Centerville. His factories produce a variety of products. Two of his product lines are polished wood clocks which he adorns with a regional theme. Naturally, clocks popular in the southwest are not as popular in the northeast, and vice versa. Each plant makes both of the clocks. These clocks are shipped to St Louis for distribution to the southeast and western states and to Pittsburg for distribution to the south and northeast.
Jack is considering streamlining his plants by removing certain production lines from certain plants. Among his options is potentially eliminating the clock production line at either the Toledo or the Centerville plant. Each plant carries a fixed operating cost for setting up the line and a unit production cost, both in terms of money and factory worker hours. This information is summarized in the table below.
 The Southwest clocks are sold for $23 each and the Northwest clocks are sold for $25 each. Demand rates used for production planning are 1875 Southwest clocks for sale out of the St Louis distribution center and 2000 Northeast clocks for sale out of the Pittsburg distribution center. Assume all these units are sold. The per clock transportation costs from plant to distribution center is given in the following table.
The Southwest clocks are sold for $23 each and the Northwest clocks are sold for $25 each. Demand rates used for production planning are 1875 Southwest clocks for sale out of the St Louis distribution center and 2000 Northeast clocks for sale out of the Pittsburg distribution center. Assume all these units are sold. The per clock transportation costs from plant to distribution center is given in the following table.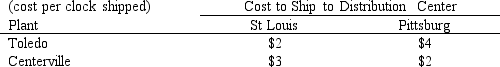 Develop a generalized network flow model for this problem and implement this model in solver. Use the model to answer the following questions.
Develop a generalized network flow model for this problem and implement this model in solver. Use the model to answer the following questions. a.
Should any of the production lines be shut down?
b.
How should worker hours be allocated to produce the clocks to meet the demand forecasts? Are there any excess hours, and if so how many?
c.
What is the expected monthly profit?
d.
If a plant is closed, what are the estimated monthly savings?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
72
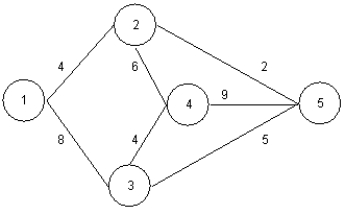
Solve the following minimal spanning tree problem starting at node 1.


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck


