Deck 10: Production and Cost Estimation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/55
Play
Full screen (f)
Deck 10: Production and Cost Estimation
1
When estimating a short-run average variable cost function,
A) the intercept must be forced to equal zero.
B) the cost data must be deflated.
C) at least one input must have been constant during the period in which the data were collected.
D) both b and c
E) all of the above
A) the intercept must be forced to equal zero.
B) the cost data must be deflated.
C) at least one input must have been constant during the period in which the data were collected.
D) both b and c
E) all of the above
both b and c
2
Refer to the following:
A short-run production function was estimated as
-At 20 units of labor, what is total product?
A) 48
B) 96
C) 20
D) 62
E) 41
A short-run production function was estimated as
-At 20 units of labor, what is total product?
A) 48
B) 96
C) 20
D) 62
E) 41
48
3
Which of the following represents a short-run cubic production function?
A)
B)
C)
D)
E) all of the above
A)
B)
C)
D)
E) all of the above
4
When estimating a short-run production function of the form , it is necessary to specify in the computer routine that
A) A < 0.
B) B > 0.
C) the intercept term is forced to equal zero.
D) a and b
E) all of the above
A) A < 0.
B) B > 0.
C) the intercept term is forced to equal zero.
D) a and b
E) all of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is an estimable form of a production function?
A) Q = f(L,K)
B) Q = f(L )
C)
D) all of the above
E) none of the above
A) Q = f(L,K)
B) Q = f(L )
C)
D) all of the above
E) none of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
6
Refer to the following:
A short-run production function was estimated as
-What is total product when average product is at its maximum level?
A) 94
B) 86
C) 100
D) 128
E) 150
A short-run production function was estimated as
-What is total product when average product is at its maximum level?
A) 94
B) 86
C) 100
D) 128
E) 150

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
7
The opportunity cost of capital owned by the firm should reflect
A) acquisition cost.
B) the return foregone by using the capital rather than renting it to another firm.
C) wage rate differences.
D) both a and b
A) acquisition cost.
B) the return foregone by using the capital rather than renting it to another firm.
C) wage rate differences.
D) both a and b

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
8
Refer to the following:
A short-run production function was estimated as
-At 20 units of labor, what is marginal product?
A) 6.0
B) 1.9
C) 6.3
D) 4.0
E) 2.4
A short-run production function was estimated as
-At 20 units of labor, what is marginal product?
A) 6.0
B) 1.9
C) 6.3
D) 4.0
E) 2.4

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
9
A potential problem with cross-section cost data is that
A) nominal cost data include the effect of inflation.
B) different firms face different input prices.
C) at least one input is fixed over time.
D) both a and b
E) none of the above
A) nominal cost data include the effect of inflation.
B) different firms face different input prices.
C) at least one input is fixed over time.
D) both a and b
E) none of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
10
A theoretical restriction on the short-run cubic cost equation, TVC = aQ + bQ + cQ2, is
A) a > 0, b > 0, c > 0
B) a > 0, b < 0, c > 0
C) a > 0, b > 0, c < 0
D) a > 0, b < 0, c < 0
A) a > 0, b > 0, c > 0
B) a > 0, b < 0, c > 0
C) a > 0, b > 0, c < 0
D) a > 0, b < 0, c < 0

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
11
Refer to the following:
A short-run production function was estimated as
-At 60 units of labor, what is marginal product?
A) 4.1
B) 1.2
C) 6.3
D) 2.4
E) -2.4
A short-run production function was estimated as
-At 60 units of labor, what is marginal product?
A) 4.1
B) 1.2
C) 6.3
D) 2.4
E) -2.4

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
12
Refer to the following:
A short-run production function was estimated as
-What is average product when it is at its maximum level?
A) 3.20
B) 8.75
C) 6.92
D) 6.00
E) 9.40
A short-run production function was estimated as
-What is average product when it is at its maximum level?
A) 3.20
B) 8.75
C) 6.92
D) 6.00
E) 9.40

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
13
An estimated short-run cost function
A) can be used to make price and output decisions.
B) holds the capital stock constant.
C) can be estimated using time-series data.
D) both a and c
E) all of the above
A) can be used to make price and output decisions.
B) holds the capital stock constant.
C) can be estimated using time-series data.
D) both a and c
E) all of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
14
A linear specification, Q = aK + bL, is not appropriate for estimating a production function because
A) the marginal products of the inputs are constant.
B) it does not allow the firm to substitute capital for labor.
C) the firm could produce positive levels of output at zero cost.
D) both b and c
E) all of the above
A) the marginal products of the inputs are constant.
B) it does not allow the firm to substitute capital for labor.
C) the firm could produce positive levels of output at zero cost.
D) both b and c
E) all of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
15
Refer to the following:
A short-run production function was estimated as
-At 60 units of labor, what is average product?
A) 9.4
B) 8.6
C) 3.7
D) 2.4
E) 6.4
A short-run production function was estimated as
-At 60 units of labor, what is average product?
A) 9.4
B) 8.6
C) 3.7
D) 2.4
E) 6.4

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
16
Refer to the following:
A short-run production function was estimated as
-At 20 units of labor, what is average product?
A) 6.0
B) 1.9
C) 6.3
D) 4.0
E) 2.4
A short-run production function was estimated as
-At 20 units of labor, what is average product?
A) 6.0
B) 1.9
C) 6.3
D) 4.0
E) 2.4

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
17
Refer to the following:
A short-run production function was estimated as
-At what level of labor usage does the maximum average product occur?
A) 20
B) 30
C) 40
D) 50
E) 60
A short-run production function was estimated as
-At what level of labor usage does the maximum average product occur?
A) 20
B) 30
C) 40
D) 50
E) 60

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
18
What is a problem with using a production function of the form Q = aK + bL (a > 0, b > 0)?
A) MRTS is constant.
B) A positive output can be produced when one input is not used.
C) The marginal products of the inputs do not have diminishing marginal returns.
D) both a and b
E) all of the above
A) MRTS is constant.
B) A positive output can be produced when one input is not used.
C) The marginal products of the inputs do not have diminishing marginal returns.
D) both a and b
E) all of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
19
With a cubic production function of the form , in order for the average and marginal product functions to have their theoretical properties, it must be the case that
A) a < 0, b > 0
B) a > 0, b < 0
C) a < 0, b < 0
D) a > 0, b > 0
A) a < 0, b > 0
B) a > 0, b < 0
C) a < 0, b < 0
D) a > 0, b > 0

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
20
An average variable cost function is estimated as Which of the following cost functions is associated with this estimate?
A) SMC = 96 - 4Q + 0.1Q2
B) TVC = 96Q - 2Q2 + 0.05Q3
C) TVC = 96Q + 4Q2 + 0.15Q3
D) SMC = 96 - 4Q + 0.15Q2
E) both b and d
A) SMC = 96 - 4Q + 0.1Q2
B) TVC = 96Q - 2Q2 + 0.05Q3
C) TVC = 96Q + 4Q2 + 0.15Q3
D) SMC = 96 - 4Q + 0.15Q2
E) both b and d

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
21
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated total variable cost (TVC)?
A) $1,348
B) $1,498
C) $2,348
D) $4,428
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated total variable cost (TVC)?
A) $1,348
B) $1,498
C) $2,348
D) $4,428

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
22
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated total variable cost (TVC)?
A) $171.40
B) $463.20
C) $1,348
D) $2,348
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated total variable cost (TVC)?
A) $171.40
B) $463.20
C) $1,348
D) $2,348

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
23
For the short-run cost function AVC = a + bQ + cQ2,
A) the AVC curve is -shaped when a < 0, b > 0, and c < 0.
B) the AVC curve is -shaped when a > 0, b < 0, and c > 0.
C) the corresponding SMC function is .
D) both a and c
E) all of the above
A) the AVC curve is -shaped when a < 0, b > 0, and c < 0.
B) the AVC curve is -shaped when a > 0, b < 0, and c > 0.
C) the corresponding SMC function is .
D) both a and c
E) all of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
24
When estimating a cubic short-run production function using linear regression analysis, you must
A) transform the equation into linear form by defining L3 and L2 as L3 and L2, respectively.
B) suppress the intercept term (regress through the origin).
C) convert to logarithms.
D) both a and b
E) both b and c
A) transform the equation into linear form by defining L3 and L2 as L3 and L2, respectively.
B) suppress the intercept term (regress through the origin).
C) convert to logarithms.
D) both a and b
E) both b and c

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
25
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated total cost (TC)?
A) $1,348
B) $1,498
C) $2,348
D) $4,428
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated total cost (TC)?
A) $1,348
B) $1,498
C) $2,348
D) $4,428

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
26
The empirical specification can be used to estimate
A) a short-run cubic production function.
B) short-run cubic cost function.
C) a family of U-shaped product curves.
D) both a and c
E) none of the above
A) a short-run cubic production function.
B) short-run cubic cost function.
C) a family of U-shaped product curves.
D) both a and c
E) none of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
27
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated average variable cost (AVC)?
A) $19.40
B) $67.40
C) $171.40
D) $179.40
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated average variable cost (AVC)?
A) $19.40
B) $67.40
C) $171.40
D) $179.40

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
28
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated short-run marginal cost (SMC)?
A) $171.40
B) $463.20
C) $1,348
D) $2,348
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated short-run marginal cost (SMC)?
A) $171.40
B) $463.20
C) $1,348
D) $2,348

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
29
The empirical specification can be used to estimate
A) a short-run cubic production function.
B) short-run cubic cost function.
C) a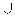 -shaped TVC curve.
-shaped TVC curve.
D) both b and c
E) none of the above
A) a short-run cubic production function.
B) short-run cubic cost function.
C) a
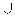 -shaped TVC curve.
-shaped TVC curve.D) both b and c
E) none of the above

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
30
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-At Straker Industries, average variable cost (AVC) reaches its minimum value at $________.
A) $24.50
B) $33.60
C) $72.80
D) $121.80
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-At Straker Industries, average variable cost (AVC) reaches its minimum value at $________.
A) $24.50
B) $33.60
C) $72.80
D) $121.80

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
31
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated average total cost (ATC)?
A) $121.93
B) $171.40
C) $463.20
D) $1,348
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated average total cost (ATC)?
A) $121.93
B) $171.40
C) $463.20
D) $1,348

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
32
Refer to the following:
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-At _______ units of labor, marginal product of labor begins to diminish.
A) 32.21
B) 44.44
C) 66.67
D) 76.66
E) 82.27
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-At _______ units of labor, marginal product of labor begins to diminish.
A) 32.21
B) 44.44
C) 66.67
D) 76.66
E) 82.27

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
33
A cubic specification for a short-run production function is appropriate when the scatter diagram indicates
A) an S-shaped total product curve.
B) marginal product of labor falls throughout the range of labor usage.
C) total product is decreasing throughout the range of labor usage.
D) an S-shaped marginal product of labor curve.
E) a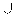 -shaped marginal product of labor curve (MP first falls and then rises as labor usage increases.
-shaped marginal product of labor curve (MP first falls and then rises as labor usage increases.
A) an S-shaped total product curve.
B) marginal product of labor falls throughout the range of labor usage.
C) total product is decreasing throughout the range of labor usage.
D) an S-shaped marginal product of labor curve.
E) a
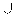 -shaped marginal product of labor curve (MP first falls and then rises as labor usage increases.
-shaped marginal product of labor curve (MP first falls and then rises as labor usage increases.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
34
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-The estimated short-run marginal cost function (SMC) at Straker Industries is:
A)
B)
C)
D)
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-The estimated short-run marginal cost function (SMC) at Straker Industries is:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
35
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated average variable cost (AVC)?
A) $28.04
B) $32.40
C) $33.33
D) $38.60
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated average variable cost (AVC)?
A) $28.04
B) $32.40
C) $33.33
D) $38.60

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
36
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated average total cost (ATC)?
A) $19.40
B) $67.40
C) $117.40
D) $1,348
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 20 units of output, what is estimated average total cost (ATC)?
A) $19.40
B) $67.40
C) $117.40
D) $1,348

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
37
Refer to the following:
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-The product curve(s) in the short-run are
A) TP = -12.96 L3 + 1,728L2.
B) AP = -12.96 L3 + 1,728L2.
C) MP = -38.88 L2 + 3,456L.
D) both a and b
E) both a and c
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-The product curve(s) in the short-run are
A) TP = -12.96 L3 + 1,728L2.
B) AP = -12.96 L3 + 1,728L2.
C) MP = -38.88 L2 + 3,456L.
D) both a and b
E) both a and c

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
38
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated short-run marginal cost (SMC)?
A) $28.04
B) $32.40
C) $33.33
D) $62.60
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated short-run marginal cost (SMC)?
A) $28.04
B) $32.40
C) $33.33
D) $62.60

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
39
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-At what level of output is average variable cost (AVC) at its minimum point for Straker Industries?
A) 0.14
B) 4.7
C) 7
D) 14
E) 28
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-At what level of output is average variable cost (AVC) at its minimum point for Straker Industries?
A) 0.14
B) 4.7
C) 7
D) 14
E) 28

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
40
Refer to the cost regression for Straker Industries shown below.
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated total cost (TC)?
A) $1,000
B) $1,463.20
C) $2,348
D) $4,428
Straker Industries estimated its short-run costs using a U-shaped average variable cost function of the form
and obtained the following results. Total fixed cost (TFC) at Straker Industries is $1,000.
-If Straker Industries produces 12 units of output, what is estimated total cost (TC)?
A) $1,000
B) $1,463.20
C) $2,348
D) $4,428

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
41
Refer to the following:
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-Marginal product when 10 units of labor are employed is
A) 12,248
B) 13,142
C) 14,287
D) 15,984
E) 30,672
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-Marginal product when 10 units of labor are employed is
A) 12,248
B) 13,142
C) 14,287
D) 15,984
E) 30,672

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
42
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, average variable cost (AVC) is
A) rising
B) falling
C) greater than short-run marginal cost
D) less than short-run marginal cost
E) both b and c
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, average variable cost (AVC) is
A) rising
B) falling
C) greater than short-run marginal cost
D) less than short-run marginal cost
E) both b and c

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
43
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, what is total cost (TC)?
A) $144,000
B) $396,000
C) $444,000
D) $642,000
E) $846,000
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, what is total cost (TC)?
A) $144,000
B) $396,000
C) $444,000
D) $642,000
E) $846,000

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
44
Refer to the following:
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-Average product when 10 units of labor are employed is
A) 12,248
B) 13,142
C) 14,287
D) 15,984
E) 30,672
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-Average product when 10 units of labor are employed is
A) 12,248
B) 13,142
C) 14,287
D) 15,984
E) 30,672

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
45
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 6,000 units, average variable cost (AVC) is
A) rising
B) falling
C) greater than short-run marginal cost
D) less than short-run marginal cost
E) both a and d
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 6,000 units, average variable cost (AVC) is
A) rising
B) falling
C) greater than short-run marginal cost
D) less than short-run marginal cost
E) both a and d

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
46
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-If Greene Enterprises produces 6,000 units of output, what is estimated average total cost (ATC)?
A) $40
B) $75.25
C) $80
D) $90
E) $168.42
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-If Greene Enterprises produces 6,000 units of output, what is estimated average total cost (ATC)?
A) $40
B) $75.25
C) $80
D) $90
E) $168.42

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
47
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, what is short-run marginal cost (SMC)?
A) $20
B) $42
C) $72
D) $90
E) $100
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, what is short-run marginal cost (SMC)?
A) $20
B) $42
C) $72
D) $90
E) $100

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
48
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-If Greene Enterprises produces 6,000 units of output, what is estimated short-run marginal cost (SMC)?
A) $45.60
B) $62.40
C) $83
D) $92
E) $100
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-If Greene Enterprises produces 6,000 units of output, what is estimated short-run marginal cost (SMC)?
A) $45.60
B) $62.40
C) $83
D) $92
E) $100

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
49
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, what is average variable cost (AVC)?
A) $20
B) $48
C) $62
D) $72
E) $85
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene's output is 2,000 units, what is average variable cost (AVC)?
A) $20
B) $48
C) $62
D) $72
E) $85

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
50
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-At Greene Enterprises, average variable cost (AVC) reaches its minimum value at $________.
A) $28.00
B) $31.67
C) $39.64
D) $43.33
E) $82.00
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-At Greene Enterprises, average variable cost (AVC) reaches its minimum value at $________.
A) $28.00
B) $31.67
C) $39.64
D) $43.33
E) $82.00

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
51
Refer to the following:
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-At ________ units of labor, average product of labor begins to diminish.
A) 32.21
B) 44.44
C) 66.67
D) 76.66
E) 82.27
A firm estimates its long-run production function to be
Suppose the firm employs 12 units of capital.
-At ________ units of labor, average product of labor begins to diminish.
A) 32.21
B) 44.44
C) 66.67
D) 76.66
E) 82.27

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
52
A short-run marginal cost function is estimated as . Which of the following cost functions is associated with this estimated SMC equation?
A) TVC = 96Q - 2Q2 + 0.05Q3
B) SMC = 96 - 4Q + 0.1Q2
C) TVC = 96Q + 4Q2 + 0.15Q3
D) AVC = 96 - 2Q + 0.05Q2
E) a and d
A) TVC = 96Q - 2Q2 + 0.05Q3
B) SMC = 96 - 4Q + 0.1Q2
C) TVC = 96Q + 4Q2 + 0.15Q3
D) AVC = 96 - 2Q + 0.05Q2
E) a and d

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
53
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-At what level of output does average variable cost (AVC) reach its minimum value for Greene Enterprises?
A) 800
B) 3,144
C) 3,800
D) 4,333
E) 51,672
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-At what level of output does average variable cost (AVC) reach its minimum value for Greene Enterprises?
A) 800
B) 3,144
C) 3,800
D) 4,333
E) 51,672

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
54
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene Enterprises produces 6,000 units, average variable cost (AVC) is $_________.
A) $40
B) $49.62
C) $55
D) $60
E) $72.46
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-When Greene Enterprises produces 6,000 units, average variable cost (AVC) is $_________.
A) $40
B) $49.62
C) $55
D) $60
E) $72.46

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
55
Refer to Greene Enterprises, Inc., whose manager recently estimated its average variable cost (AVC) function to be
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-What is total variable cost (TVC) at Greene Enterprises when average variable cost (AVC) is at its minimum?
A) $48,000
B) $101,101
C) $137,222
D) $190,476
E) $437,212
Greene Enterprises faces total fixed costs (TFC) of $300,000.
-What is total variable cost (TVC) at Greene Enterprises when average variable cost (AVC) is at its minimum?
A) $48,000
B) $101,101
C) $137,222
D) $190,476
E) $437,212

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck


