Deck 5: Analytic Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/265
Play
Full screen (f)
Deck 5: Analytic Trigonometry
1
Use the figure to find the exact value of the trigonometric function.
Sec 2
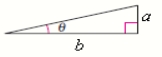
a = 1, b = 8
A)
B)
C)
D)
E)
Sec 2

a = 1, b = 8
A)
B)
C)
D)
E)
2
Use the half-angle formulas to simplify the expression.
A)|sin 5x|
B)- |sin x|
C)|sin 10x|
D)- |sin 5x|
E)|sin x|
A)|sin 5x|
B)- |sin x|
C)|sin 10x|
D)- |sin 5x|
E)|sin x|
|sin 5x|
3
Use the figure to find the exact value of the trigonometric function.
Sin 2
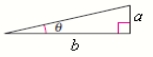
A = 1, b = 2
A)
B) ..
C)
D)
E) ..
Sin 2

A = 1, b = 2
A)
B) ..
C)
D)
E) ..
..
4
Use the figure to find the exact value of the trigonometric function.
Cot 2
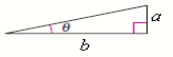
a = 1, b = 6
A)
B)
C)
D)
E)
Cot 2

a = 1, b = 6
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
5
Use a double-angle formula to rewrite the expression.
3 - 6 sin2 x
A)6 cos x
B)3 sin 2x
C)3 sin x
D)3 cos 2x
E)6 cos 2x
3 - 6 sin2 x
A)6 cos x
B)3 sin 2x
C)3 sin x
D)3 cos 2x
E)6 cos 2x

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
6
Use the half-angle formulas to simplify the expression.
A) - |cot x|
B) - |3 tan x|
C) - |3 tan 6x|
D) - |3 cot 3x|
E) - |cot 3x|
A) - |cot x|
B) - |3 tan x|
C) - |3 tan 6x|
D) - |3 cot 3x|
E) - |cot 3x|

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
7
Use the figure to find the exact value of the trigonometric function.
Tan 2
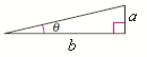
a = 1, b = 6
A)
B)
C)
D)
E)
Tan 2

a = 1, b = 6
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
8
Use the sum-to-product formulas to rewrite the sum or difference as a product.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
9
Use a double-angle formula to rewrite the expression.
2 sin2 x - 1
A)cos x
B)cos 2x
C)-2 cos x
D)2 cos 2x
E)- cos 2x
2 sin2 x - 1
A)cos x
B)cos 2x
C)-2 cos x
D)2 cos 2x
E)- cos 2x

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
10
Use the figure to find the exact value of the trigonometric function.
Csc 2
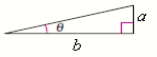
a = 1, b = 6
A)
B)
C)
D)
E)
Csc 2

a = 1, b = 6
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
11
Use the half-angle formulas to simplify the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
12
Use the product-to-sum formulas to rewrite the product as a sum or difference.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
13
Use the product-to-sum formulas to rewrite the product as a sum or difference.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
14
Use the sum-to-product formulas to rewrite the sum or difference as a product.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
15
Use a double-angle formula to rewrite the expression.
10 cos2 x - 5
A)5 cos x
B)cos 5x
C)10 cos 2x
D)10 cos x
E)5 cos 2x
10 cos2 x - 5
A)5 cos x
B)cos 5x
C)10 cos 2x
D)10 cos x
E)5 cos 2x

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
16
Use the product-to-sum formulas to rewrite the product as a sum or difference.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
17
Use the figure to find the exact value of the trigonometric function.
Cos 2
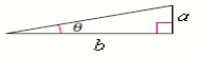
a = 1, b = 2
A)
B)
C)
D)
E)
Cos 2

a = 1, b = 2
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
18
Use a double-angle formula to rewrite the expression.
A) sin x
B) 2 sin x
C) 2 sin 2x.
D) sin x..
E) sin 2x
A) sin x
B) 2 sin x
C) 2 sin 2x.
D) sin x..
E) sin 2x

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
19
Use the half-angle formulas to simplify the expression.
A) - |cos x|
B) |cos x|
C) |cos 4x|
D)- |cos 4x|
E) - |cos 8x|
A) - |cos x|
B) |cos x|
C) |cos 4x|
D)- |cos 4x|
E) - |cos 8x|

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
20
Use the product-to-sum formulas to rewrite the product as a sum or difference.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
21
Find the exact solutions of the given equation in the interval [0, 2 ).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
22
Use the figure below to determine the exact value of the given function. 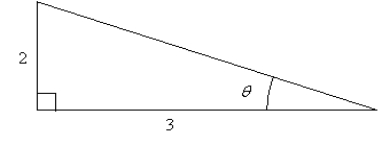
A)
B)
C) .
D)
E)

A)
B)
C) .
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
23
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
24
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
25
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
26
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
27
Use a double-angle formula to find the exact value of cos2u when
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
28
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
29
Use the figure to find the exact value of the trigonometric function. 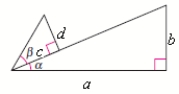
Cos 2
A)
B)
C)
D)
E)

Cos 2
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
30
Use the sum-to-product formulas to rewrite the sum or difference as a product.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
31
Use a double angle formula to rewrite the given expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
32
Use the sum-to-product formulas to rewrite the sum or difference as a product.
Cos 3 + cos 8
A)
B)
C)
D)
E)
Cos 3 + cos 8
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
33
Convert the expression.
A)2 cos b
B) cos 2b
C) cos b
D)2 cos 2b
E) 4 cos b
A)2 cos b
B) cos 2b
C) cos b
D)2 cos 2b
E) 4 cos b

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
34
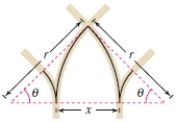
When two railroad tracks merge, the overlapping portions of the tracks are in the shapes of circular arcs (see figure).The radius of each arc r (in feet) and the angle are related by
Write a formula for x in terms of cos .
A)
B)
C)
D)
E)
Write a formula for x in terms of cos .

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
35
Use the sum-to-product formulas to select the sum or difference as a product.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
36
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
37
Find the exact solutions of the given equation in the interval [0, 2 ).
A)
B)
C)
D) x = 0
E)
A)
B)
C)
D) x = 0
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
38
The mach number M of an airplane is the ratio of its speed to the speed of sound.When an airplane travels faster than the speed of sound, the sound waves form a cone behind the airplane (see figure).The mach number is related to the apex angle of the cone by . 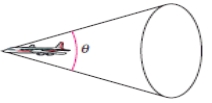
Rewrite the equation in terms of .
A)
B)
C)
D)
E)

Rewrite the equation in terms of .
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
39
Use the figure to find the exact value of the trigonometric function. 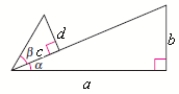
Sin 2
A)
B)
C)
D)
E)

Sin 2
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
40
Convert the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
41
The range of a projectile fired at an angle with the horizontal and with an initial velocity of v0 feet per second is where r is measured in feet.A golfer strikes a golf ball at 90 feet per second.Ignoring the effects of air resistance, at what angle must the golfer hit the ball so that it travels 150 feet? (Round your answer to the nearest degree.)
A)14°
B)36°
C)18°
D)27°
E)41°
A)14°
B)36°
C)18°
D)27°
E)41°

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
42
Use the figure below to find the exact value of the given trigonometric expression. 
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
43
Find the expression as the sine of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
44
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
45
Find all solutions of the given equation in the interval [0, 2 ).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
46
Find the expression as the tangent of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
47
Use the sum-to-product formulas to find the exact value of the given expression.
A)
B) 1
C)
D)-1
E)0
A)
B) 1
C)
D)-1
E)0

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
48
Use the half-angle formula to simplify the given expression.
A) cos |2x|
B) cos |8x|
C) cos |16x|
D) cos |32x|
E) cos |4x|
A) cos |2x|
B) cos |8x|
C) cos |16x|
D) cos |32x|
E) cos |4x|

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
49
Find the expression as the tangent of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
50
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
51
Find the expression as the sine of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
52
Find all solutions of the given equation in the interval [0, 2 ).
A)
B)
C)
D)
E) x = 0
A)
B)
C)
D)
E) x = 0

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
53
Find the expression as the sine or cosine of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
54
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
55
Find the expression as the cosine of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
56
Use the sum-to-product formulas to write the given expression as a product.
A) 2 sin 4 cos
B) -2 sin 4 sin
C)- 2 cos 4 cos
D) 2 cos 4 sin
E) 2 cos 4 cos
A) 2 sin 4 cos
B) -2 sin 4 sin
C)- 2 cos 4 cos
D) 2 cos 4 sin
E) 2 cos 4 cos

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
57
Use the half-angle formulas to determine the exact value of the given trigonometric expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
58
Use the product-to-sum formula to write the given product as a sum or difference.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
59
Find the expression as the sine or cosine of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
60
Find the expression as the tangent of an angle.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
61
A weight is attached to a spring suspended vertically from a ceiling.When a driving force is applied to the system, the weight moves vertically from its equilibrium position, and this motion is modeled by
where y is the distance from equilibrium (in feet) and t is the time (in seconds).
Find the amplitude of the oscillations of the weight.
A)
B)
C)
D)
E)
where y is the distance from equilibrium (in feet) and t is the time (in seconds).
Find the amplitude of the oscillations of the weight.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
62
Simplify the expression algebraically.
A)-
B)
C)
D)
E)
A)-
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
63
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
64
A weight is attached to a spring suspended vertically from a ceiling.When a driving force is applied to the system, the weight moves vertically from its equilibrium position, and this motion is modeled by
Where y is the distance from equilibrium (in feet) and t is the time (in seconds).
Use the identity where , to write the model in the form .
A)
B)
C)
D)
E)
Where y is the distance from equilibrium (in feet) and t is the time (in seconds).
Use the identity where , to write the model in the form .
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
65
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
66
Use the formula , where , to rewrite the trigonometric expression in the form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
67
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
68
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
69
Use the formula , where to rewrite the trigonometric expression in the following form.
A)
B)
C)3
D)
E)
A)
B)
C)3
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
70
Use the formula , where , to rewrite the trigonometric expression in the form 9
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
71
Use the formula , where to rewrite the trigonometric expression in the following form.
A)
B)9
C)9
D)
E)2
A)
B)9
C)9
D)
E)2

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
72
Use the formula , where , to rewrite the trigonometric expression in the following form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
73
Use the formula , where , to rewrite the trigonometric expression in the following form.
A)2
B)
C)
D)2
E)8
A)2
B)
C)
D)2
E)8

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
74
Simplify the expression algebraically.
A)
B)0
C)
D)1
E)6
A)
B)0
C)
D)1
E)6

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
75
Use the formula , where , to rewrite the trigonometric expression in the following form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
76
Use the formula , where to rewrite the trigonometric expression in the following form.
A)
B)
C)7
D)3
E)3
A)
B)
C)7
D)3
E)3

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
77
Use the formula , where to rewrite the trigonometric expression in the following form.
A)6
B)
C)
D)13
E)13
A)6
B)
C)
D)13
E)13

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
78
Simplify the expression algebraically.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
79
Use a graphing utility to select correct graph of and in the same viewing window.Use the graphs to determine whether .Explain your reasoning.
A)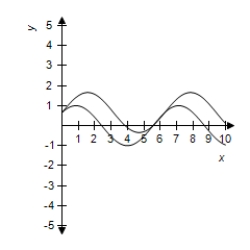 No, because their graphs are different.
No, because their graphs are different.
B)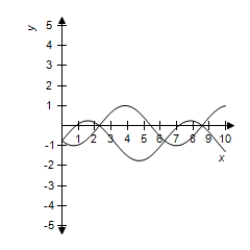 Yes, because their graphs are different.
Yes, because their graphs are different.
C)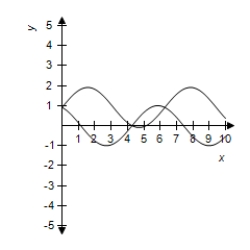 Yes, because their graphs are same.
Yes, because their graphs are same.
D)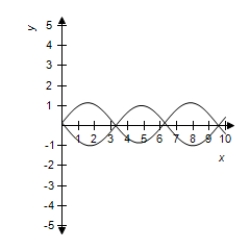 No, because their graphs are Same.
No, because their graphs are Same.
E)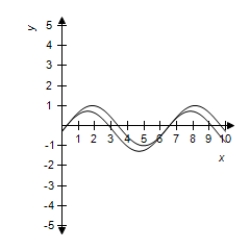 No, because their graphs are different.
No, because their graphs are different.
A)
 No, because their graphs are different.
No, because their graphs are different.B)
 Yes, because their graphs are different.
Yes, because their graphs are different.C)
 Yes, because their graphs are same.
Yes, because their graphs are same.D)
 No, because their graphs are Same.
No, because their graphs are Same.E)
 No, because their graphs are different.
No, because their graphs are different.
Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck
80
Use the formula , where , to rewrite the trigonometric expression in the following form.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 265 flashcards in this deck.
Unlock Deck
k this deck


