Deck 4: Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/384
Play
Full screen (f)
Deck 4: Trigonometry
1
The designers of a water park are creating a new slide and have sketched some preliminary drawings.The length of the ladder is a = 26 feet, and its angle of elevation is 60º (see figure).
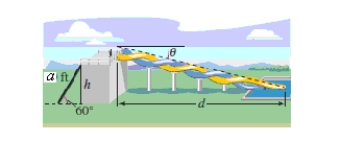
Find the angle of depression from the top of the slide to the end of the slide at the ground in terms of the horizontal distance d the rider travels.
A)
B)
C)
D)
E)

Find the angle of depression from the top of the slide to the end of the slide at the ground in terms of the horizontal distance d the rider travels.
A)
B)
C)
D)
E)
2
You are holding one of the tethers attached to the top of a giant character balloon in a parade.Before the start of the parade the balloon is upright and the bottom is floating approximately 20 feet above ground level.You are standing approximately a = 100 feet ahead of the balloon (see figure).Round your answer to two decimal places. 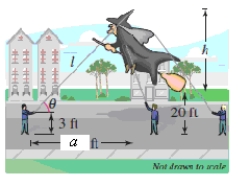
Find the height h of the balloon if the angle of elevation to the top of the balloon is 35º.
A)55.02 ft
B)56.02 ft
C)53.02 ft
D)57.02 ft
E)54.02 ft

Find the height h of the balloon if the angle of elevation to the top of the balloon is 35º.
A)55.02 ft
B)56.02 ft
C)53.02 ft
D)57.02 ft
E)54.02 ft
53.02 ft
3
A cellular telephone tower that is 150 feet tall is placed on top of a mountain that is 1200 feet above sea level.What is the angle of depression from the top of the tower to a cell phone user who is 6 horizontal miles away and 400 feet above sea level? Round your answer to two decimal places.
A)3.72º
B)1.72º
C)5.72º
D)4.72º
E)2.72º
A)3.72º
B)1.72º
C)5.72º
D)4.72º
E)2.72º
1.72º
4
The sun is 20º above the horizon.Find the length of a shadow cast by a park statue that is 30 feet tall.Approximate the answer to two decimal places.
A)82.42 ft
B)84.42 ft
C)85.42 ft
D)83.42 ft
E)86.42 ft
A)82.42 ft
B)84.42 ft
C)85.42 ft
D)83.42 ft
E)86.42 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
5
A ladder 17 feet long leans against the side of a house.Find the height from the top of the ladder to the ground if the angle of elevation of the ladder is 80º.Approximate the answer to one decimal place.
A)19.7 ft
B)20.7 ft
C)18.7 ft
D)16.7 ft
E)17.7 ft
A)19.7 ft
B)20.7 ft
C)18.7 ft
D)16.7 ft
E)17.7 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
6
A Global Positioning System satellite orbits a = 13,000 miles above Earth's surface (see figure).Find the angle of depression from the satellite to the horizon.Assume the radius of Earth is 4000 miles.Round your answer to two decimal places. 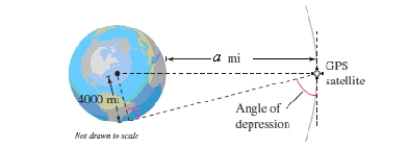
A)77.39º
B)78.39º
C)79.39º
D)76.39º
E)80.39º

A)77.39º
B)78.39º
C)79.39º
D)76.39º
E)80.39º

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
7
An engineer erects a 111-foot cellular telephone tower.Find the angle of elevation to the top of the tower at a point on level ground 62 feet from its base.Round your answer to one decimal place.
A)60.8º
B)64.8º
C)63.8º
D)61.8º
E)62.8º
A)60.8º
B)64.8º
C)63.8º
D)61.8º
E)62.8º

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the right triangle shown in the figure for all unknown sides and angles.Round your answers to two decimal places. 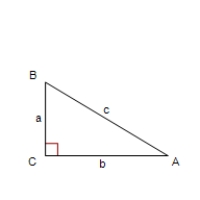
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
9
The sun is 25º above the horizon.Find the length of a shadow cast by a building that is feet tall (see figure).Approximate the answer to two decimal places. 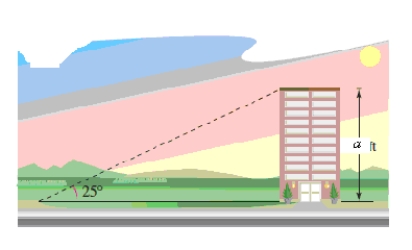
A)281.79 ft
B)278.79 ft
C)279.79 ft
D)280.79 ft
E)282.79 ft

A)281.79 ft
B)278.79 ft
C)279.79 ft
D)280.79 ft
E)282.79 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
10
The designers of a water park are creating a new slide and have sketched some preliminary drawings.The length of the ladder is a = 24 feet, and its angle of elevation is 60º (see figure).
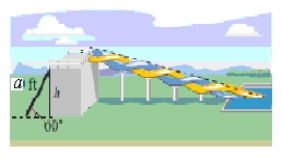
Find the height of the slide.Round your answer to two decimal places.
A)About 21.78 ft
B)About 22.78 ft
C)About 23.78 ft
D)About 20.78 ft
E)About 24.78 ft

Find the height of the slide.Round your answer to two decimal places.
A)About 21.78 ft
B)About 22.78 ft
C)About 23.78 ft
D)About 20.78 ft
E)About 24.78 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
11
The length of a shadow of a tree is 120 feet when the angle of elevation of the sun is 33º.Approximate the height of the tree.Approximate the answer to one decimal place.
A)77.9 ft
B)81.9 ft
C)79.9 ft
D)78.9 ft
E)80.9 ft
A)77.9 ft
B)81.9 ft
C)79.9 ft
D)78.9 ft
E)80.9 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
12
A police department has set up a speed enforcement zone on a straight length of highway.A patrol car is parked parallel to the zone, a = 210 feet from one end and b = 130 feet from the other end (see figure). 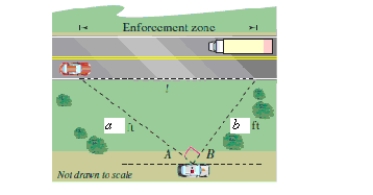
Find the length l of the zone.Round your answer to two decimal places.
A)286.98 ft
B)276.98 ft
C)266.98 ft
D)246.98 ft
E)256.98 ft

Find the length l of the zone.Round your answer to two decimal places.
A)286.98 ft
B)276.98 ft
C)266.98 ft
D)246.98 ft
E)256.98 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
13
An observer in a lighthouse a = 340 feet above sea level observes two ships directly offshore. The angles of depression to the ships are 4º and 6.5º (see figure).How far apart are the ships? Round your answer to one decimal place.
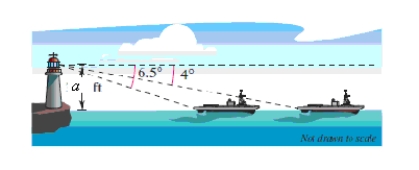
A)1878.1 ft
B)1879.1 ft
C)1880.1 ft
D)1881.1 ft
E)1882.1 ft

A)1878.1 ft
B)1879.1 ft
C)1880.1 ft
D)1881.1 ft
E)1882.1 ft

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
14
Find the altitude of the isosceles triangle shown in the figure.Round your answer to two decimal places. 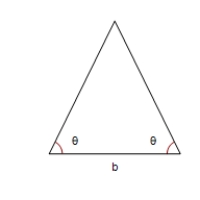
A)2.00
B)11.00
C)5.50
D)22.00
E)7.50

A)2.00
B)11.00
C)5.50
D)22.00
E)7.50

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
15
You are holding one of the tethers attached to the top of a giant character balloon in a parade.Before the start of the parade the balloon is upright and the bottom is floating approximately 20 feet above ground level.You are standing approximately a = 130 feet ahead of the balloon (see figure). 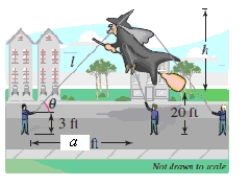
Find the length l of the tether you are holding in terms of h, the height h of the balloon from top to bottom.
A)
B)
C)
D)
E)

Find the length l of the tether you are holding in terms of h, the height h of the balloon from top to bottom.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
16
For the simple harmonic motion described by the trigonometric function, find the least positive value of t for which d = 0.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
17
You are holding one of the tethers attached to the top of a giant character balloon in a parade.Before the start of the parade the balloon is upright and the bottom is floating approximately 20 feet above ground level.You are standing approximately a = 130 feet ahead of the balloon (see figure). 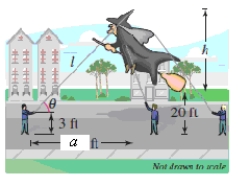
Find an expression for the angle of elevation from you to the top of the balloon.
A)
B)
C)
D)
E)

Find an expression for the angle of elevation from you to the top of the balloon.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
18
A passenger in an airplane at an altitude of a = 20 kilometers sees two towns directly to the east of the plane.The angles of depression to the towns are 28º and 55º (see figure).How far apart are the towns? How far apart are the ships? Round your answer to one decimal place. 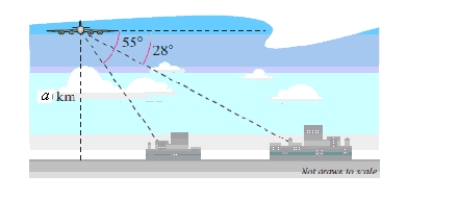
A)23.6 km
B)24.6 km
C)25.6 km
D)26.6 km
E)27.6 km

A)23.6 km
B)24.6 km
C)25.6 km
D)26.6 km
E)27.6 km

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
19
For the simple harmonic motion described by the trigonometric function, find the least positive value of t for which d = 0.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
20
The height of an outdoor basketball backboard is feet, and the backboard casts a shadow feet long. Find the angle of elevation of the sun.Round your answer to one decimal place.
A)36.0º
B)37.0º
C)35.0º
D)39.0º
E)38.0º
A)36.0º
B)37.0º
C)35.0º
D)39.0º
E)38.0º

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
21
For the simple harmonic motion described by the trigonometric function, find the least positive value of t for which
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
22
For the simple harmonic motion described by the trigonometric function, find the frequency per second.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
23
For the simple harmonic motion described by the trigonometric function, find the maximumvalue of d when . Round your answer to nearest whole number.
A)1
B)10
C)6
D)5
E)0
A)1
B)10
C)6
D)5
E)0

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
24
Find the angle between two nonvertical lines and .The angle satisfies the equation
Where and are slopes of and , respectively.
(Assume that .)
: 5x - 4y = 5 : x + y = 1
Round your answer to one decimal place.
A)83.7º
B)84.7º
C)85.7º
D)86.7º
E)87.7º
Where and are slopes of and , respectively.
(Assume that .)
: 5x - 4y = 5 : x + y = 1
Round your answer to one decimal place.
A)83.7º
B)84.7º
C)85.7º
D)86.7º
E)87.7º

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
25
For the simple harmonic motion described by the trigonometric function, find the maximum displacement.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
26
A point on the end of a tuning fork moves in simple harmonic motion described by
Find given that the tuning fork for middle C has a frequency 270 of vibrations per second.
A)
B)
C)
D)
E)
Find given that the tuning fork for middle C has a frequency 270 of vibrations per second.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
27
For the simple harmonic motion described by the trigonometric function, find the maximum displacement.
A)
B)
C) 8
D)
E)
A)
B)
C) 8
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
28
Find the length of the sides of a regular pentagon inscribed in a circle of radius 26 inches.Round your answer to one decimal place.
A)31.6 in.
B)33.6 in.
C)30.6 in.
D)32.6 in.
E)34.6 in.
A)31.6 in.
B)33.6 in.
C)30.6 in.
D)32.6 in.
E)34.6 in.

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
29
For the simple harmonic motion described by the trigonometric function, find the frequency per second.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
30
Determine the angle between the diagonal of a cube and the diagonal of its base, as shown in the figure, where .Round your answer to one decimal place.
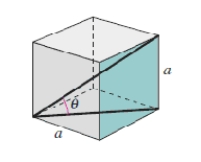
A)38.3o
B)36.3o
C)39.3o
D)35.3o
E)37.3o

A)38.3o
B)36.3o
C)39.3o
D)35.3o
E)37.3o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
31
Find a model for simple harmonic motion satisfying the specified conditions.
Displacement (t = 0): 0
Amplitude: 5 meters
Period: 10 seconds
A)
B)
C)
D)
E)
Displacement (t = 0): 0
Amplitude: 5 meters
Period: 10 seconds
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
32
Find the length of the sides of a regular hexagon inscribed in a circle of radius 29 inches.
A)30 in.
B)31 in.
C)32 in.
D)33 in.
E)29 in.
A)30 in.
B)31 in.
C)32 in.
D)33 in.
E)29 in.

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
33
Find the angle between two nonvertical lines and .The angle satisfies the equation
Where and are slopes of and , respectively.
(Assume that .)
Round your answer to one decimal place.
A)54.1o
B) 53.1o
C)55.1o
D)52.1o
E)56.1o
Where and are slopes of and , respectively.
(Assume that .)
Round your answer to one decimal place.
A)54.1o
B) 53.1o
C)55.1o
D)52.1o
E)56.1o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
34
Find the distance y across the flat sides of a hexagonal nut (see figure). cm Round your answer to two decimal places.
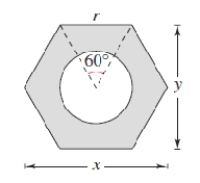
A) cm
B) cm
C) cm
D) cm
E) cm

A) cm
B) cm
C) cm
D) cm
E) cm

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
35
Determine the angle between the diagonal of a cube and its edge, as shown in the figure, where .Round your answer to one decimal place. 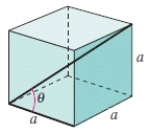
A)56.7o
B)57.7o
C)55.7o
D)54.7o
E)58.7o

A)56.7o
B)57.7o
C)55.7o
D)54.7o
E)58.7o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
36
For the simple harmonic motion described by the trigonometric function, find the frequency per second.
A)16
B)
C)12
D)2
E)6
A)16
B)
C)12
D)2
E)6

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
37
For the simple harmonic motion described by the trigonometric function, find the maximum displacement.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
38
A ball that is bobbing up and down on the end of a spring has a maximum displacement of 3 inches.Its motion (in ideal conditions) is modeled by
where y is measured in feet and t is the time in seconds.
What is the period of the oscillations ?
A)
B)
C)
D)
E)
where y is measured in feet and t is the time in seconds.
What is the period of the oscillations ?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
39
Find a model for simple harmonic motion satisfying the specified conditions.
Displacement (t = 0): 0
Amplitude: 5 centimeters
Period: 2 seconds
A)
B)
C)
D)
E)
Displacement (t = 0): 0
Amplitude: 5 centimeters
Period: 2 seconds
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
40
Find the lengths of all the unknown members of the truss. Round your answer to one decimal place.
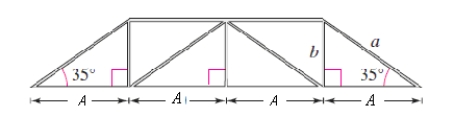
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the expression.Round your result to two decimal places.
A)2.20
B)0.20
C)3.20
D)-0.80
E)1.20
A)2.20
B)0.20
C)3.20
D)-0.80
E)1.20

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the expression.Round your result to two decimal places.
A)-0.66
B)2.34
C)1.34
D)3.34
E)0.34
A)-0.66
B)2.34
C)1.34
D)3.34
E)0.34

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
43
A plane is 52 miles west and 46 miles north of an airport.The pilot wants to fly directly to the airport.What bearing should the pilot take? Answer should be given in degrees and minutes.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
44
Evaluate the expression.Round your result to two decimal places.
A)-1.53
B)-0.53
C)2.47
D)0.47
E)1.47
A)-1.53
B)-0.53
C)2.47
D)0.47
E)1.47

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the expression.Round your result to two decimal places.
A)1.87
B)-2.13
C)-1.13
D)0.87
E)-0.13
A)1.87
B)-2.13
C)-1.13
D)0.87
E)-0.13

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
46
After leaving the runway, a plane's angle of ascent is 17o and its speed is 278 feet per second.How many minutes will it take for the airplane to climb to a height of 11,500 feet? Round answer to two decimal places.
A)0.69 minutes
B)2.36 minutes
C)0.72 minutes
D)1.25 minutes
E)1.81 minutes
A)0.69 minutes
B)2.36 minutes
C)0.72 minutes
D)1.25 minutes
E)1.81 minutes

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
47
Find the altitude of the isosceles triangle shown below if and .Round answer to two decimal places. 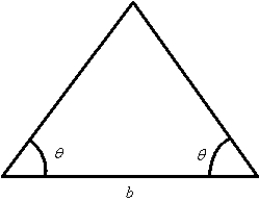
A)33.18 meters
B)6.23 meters
C)9.98 meters
D)16.59 meters
E)9.42 meters

A)33.18 meters
B)6.23 meters
C)9.98 meters
D)16.59 meters
E)9.42 meters

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the expression.Round your result to two decimal places.
A)4.21
B)2.21
C)3.21
D)0.21
E)1.21
A)4.21
B)2.21
C)3.21
D)0.21
E)1.21

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
49
Find the altitude of the isosceles triangle shown below if and .Round your answer to two decimal places. 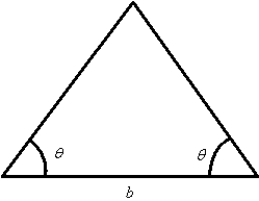
A)5.12 centimeters
B)6.25 centimeters
C)3.13 centimeters
D)2.46 centimeters
E)1.38 centimeters

A)5.12 centimeters
B)6.25 centimeters
C)3.13 centimeters
D)2.46 centimeters
E)1.38 centimeters

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
50
Evaluate the expression.Round your result to two decimal places.
A)3.54
B)0.54
C)1.54
D)2.54
E)-0.46
A)3.54
B)0.54
C)1.54
D)2.54
E)-0.46

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
51
A granular substance such as sand naturally settles into a cone-shaped pile when poured from a small aperture.Its height depends on the humidity and adhesion between granules.The angle of elevation of a pile, θ, is called the angle of repose.If the height of a pile of sand is 11 feet and its diameter is approximately 34 feet, determine the angle of repose.Round answer to nearest degree. 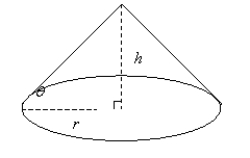
A)29o
B)30o
C)31o
D)32o
E)33o

A)29o
B)30o
C)31o
D)32o
E)33o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
52
A land developer wants to find the distance across a small lake in the middle of his proposed development.The bearing from A to B is .The developer leaves point A and travels 74 yards perpendicular to to point C.The bearing from C to point B is .Determine the distance, AB, across the small lake.Round distance to nearest yard. 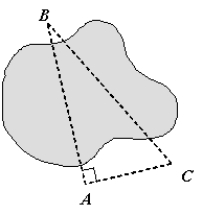
A)169 yards
B)114 yards
C)139 yards
D)154 yards
E)121 yards

A)169 yards
B)114 yards
C)139 yards
D)154 yards
E)121 yards

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the expression.Round your result to two decimal places.
A)2.12
B)0.12
C)1.12
D)-0.88
E)3.12
A)2.12
B)0.12
C)1.12
D)-0.88
E)3.12

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate the expression.Round your result to two decimal places.
A)1.73
B)-0.27
C)-1.27
D)2.73
E)0.73
A)1.73
B)-0.27
C)-1.27
D)2.73
E)0.73

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
55
If the sides of a rectangular solid are as shown, and , determine the angle, , between the diagonal of the base of the solid and the diagonal of the solid.Round answer to two decimal places. 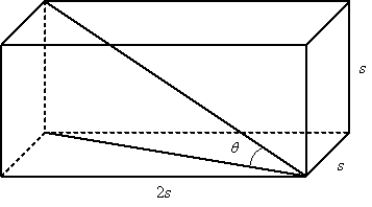
A)21.91o
B)24.09o
C)17.21o
D)26.28o
E)19.86o

A)21.91o
B)24.09o
C)17.21o
D)26.28o
E)19.86o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
56
After leaving the runway, a plane's angle of ascent is 17o and its speed is 280 feet per second.How many minutes will it take for the airplane to climb to a height of 11,000 feet? Round your answer to two decimal places.
A)1.72 minutes
B)1.19 minutes
C)2.24 minutes
D)0.65 minutes
E)0.68 minutes
A)1.72 minutes
B)1.19 minutes
C)2.24 minutes
D)0.65 minutes
E)0.68 minutes

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
57
If and , determine the value of A.Round to two decimal places. 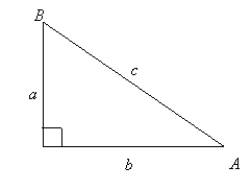
A)48.19o
B)56.31o
C)33.69o
D)41.81o
E)53.19o

A)48.19o
B)56.31o
C)33.69o
D)41.81o
E)53.19o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
58
If and , determine the value of B.Round to two decimal places. 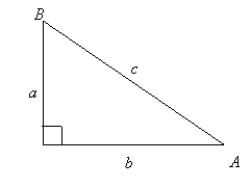
A)68.55o
B)66.87o
C)28.13o
D)21.45o
E)23.13o

A)68.55o
B)66.87o
C)28.13o
D)21.45o
E)23.13o

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
59
The angle of elevation of the sun is 26o.Find the length, l, of a shadow cast by a tree that is 38 feet tall.Round your answer to two decimal places.
A) feet
B) feet
C) feet
D) feet
E) feet
A) feet
B) feet
C) feet
D) feet
E) feet

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate the expression.Round your result to two decimal places.
A)2.71
B)-0.29
C)1.71
D)0.71
E)-1.29
A)2.71
B)-0.29
C)1.71
D)0.71
E)-1.29

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
61
Find an algebraic expression that is equivalent to the expression..
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
62
Find an algebraic expression that is equivalent to the expression.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the expression.Round your result to two decimal places.
A)-0.53
B)-1.53
C)0.47
D)-3.53
E)-2.53
A)-0.53
B)-1.53
C)0.47
D)-3.53
E)-2.53

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
64
A boat is pulled in by means of a winch located on a dock feet above the deck of the boat (see figure).Let be the angle of elevation from the boat to the winch and let s be the length of the rope from the winch to the boat.Write as a function of s. 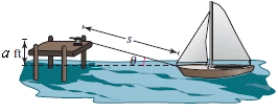
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
65
Use the properties of inverse trigonometric functions to evaluate the expression.
A)1
B)-1
C)
D)0
E)
A)1
B)-1
C)
D)0
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
66
Use an inverse trigonometric function to write as a function of x. 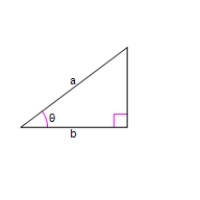
A = 5x
B = x + 9
A)
B)
C)
D)
E)
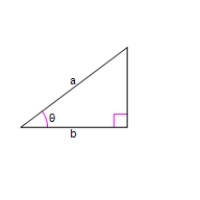
A = 5x
B = x + 9
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
67
Use an inverse trigonometric function to write as a function of x. 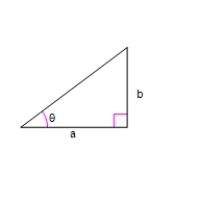
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate the expression.Round your result to two decimal places.
A)0.30
B)1.30
C)4.30
D)3.30
E)2.30
A)0.30
B)1.30
C)4.30
D)3.30
E)2.30

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
69
A television camera at ground level is filming the lift-off of a space shuttle at a point meters from the launch pad (see figure).Let be the angle of elevation to the shuttle and let s be the height of the shuttle.Write as a function of s. 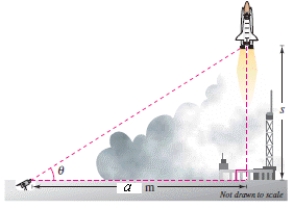
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
70
Find an algebraic expression that is equivalent to the expression..
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
71
Find the value of the expression.Round your result to two decimal places.
A)-1.25
B)1.25
C)1.89
D)3.14
E)-3.14
A)-1.25
B)1.25
C)1.89
D)3.14
E)-3.14

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
72
Use an inverse trigonometric function to write as a function of x. 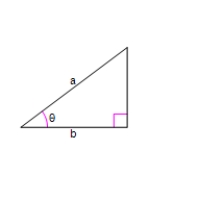
A = x
B = 10
A)
B)
C)
D)
E)
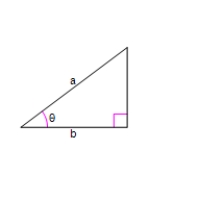
A = x
B = 10
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
73
A security car with its spotlight on is parked meters from a warehouse.Consider and x as shown in the figure.Write as a function of x. 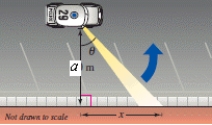
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
74
Use an inverse trigonometric function to write as a function of x. 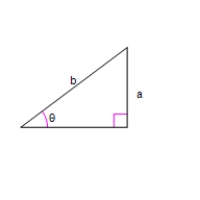
A = x + 6
B = 2
A)
B)
C)
D)
E)

A = x + 6
B = 2
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
75
Use the properties of inverse trigonometric functions to evaluate the expression.
A)
B)
C)0.4
D)
E)
A)
B)
C)0.4
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the expression.Round your result to two decimal places.
A)-3.53
B)0.47
C)-0.53
D)-1.53
E)-2.53
A)-3.53
B)0.47
C)-0.53
D)-1.53
E)-2.53

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
77
An airplane flies at an altitude of miles toward a point directly over an observer.Consider and x as shown in the figure.Write as a function of x. 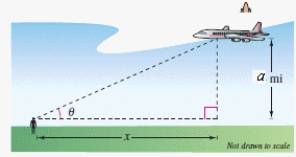
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
78
Use an inverse trigonometric function to write as a function of x. 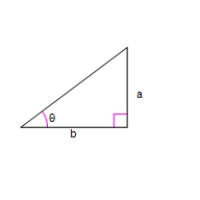
A = x
B = 6
A)
B)
C)
D)
E)
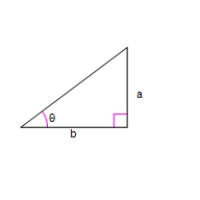
A = x
B = 6
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
79
Use an inverse trigonometric function to write as a function of x. 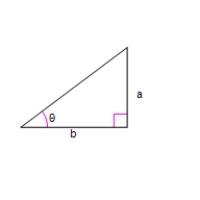
A = x + 5
B = 10
A)
B)
C)
D)
E)
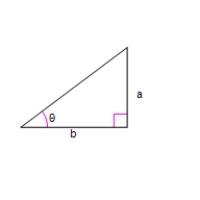
A = x + 5
B = 10
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck
80
Use the properties of inverse trigonometric functions to evaluate the expression.
A)
B)
C)
D)
E)40
A)
B)
C)
D)
E)40

Unlock Deck
Unlock for access to all 384 flashcards in this deck.
Unlock Deck
k this deck


