Deck 11: Experimental Design and Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/98
Play
Full screen (f)
Deck 11: Experimental Design and Analysis of Variance
1
In one-way ANOVA,other factors being equal,the further apart the treatment means are from each other,the more likely we are to reject the null hypothesis associated with the ANOVA F test.
True
2
The experimentwise α for the 95 percent individual confidence interval for μ1 - μ2 (treatment mean 1 - treatment mean 2)will always be smaller than the experimentwise α for a Tukey 95 percent simultaneous confidence interval for μ1 - μ2.
False
3
The error sum of squares measures the between-treatment variability.
False
4
If sample mean plots look essentially parallel,we can intuitively conclude that there is an interaction between the two factors.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
5
The ANOVA procedure for a two-factor factorial experiment partitions the total sum of squares into three components,SS first factor,SS second factor,and SSE.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
6
Interaction exists between two factors if the relationship between the mean response and one factor depends on the other factor.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
7
If factors being studied cannot be controlled,the data are said to be observational.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
8
In a 2-way ANOVA,if factor 1 has a levels and factor 2 has b levels,then there are a total of _______ treatments.
A)a + b
B)a × b
C)|a - b|
D)a/b
E)a
A)a + b
B)a × b
C)|a - b|
D)a/b
E)a

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
9
In a 2-way ANOVA,treatment is considered to be a combination of a level of factor 1 and a level of factor 2.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
10
In one-way ANOVA,the numerator degrees of freedom equals the number of samples being compared.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
11
After rejecting the null hypothesis of equal treatments,a researcher decided to compute a 95 percent confidence interval for the difference between the mean of treatment 1 and mean of treatment 2 based on the Tukey procedure.At α = .05,if the confidence interval includes the value of zero,then we can reject the hypothesis that the two population means are equal.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
12
In one-way ANOVA,as the between-treatment variation decreases,the probability of rejecting the null hypothesis increases.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
13
The 95 percent individual confidence interval for μ1 - μ2 (treatment mean 1 - treatment mean 2)will always be smaller than the Tukey 95 percent simultaneous confidence interval for μ1 - μ2.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
14
In one-way ANOVA,a large value of F results when the within-treatment variability is large compared to the between-treatment variability.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
15
When using a randomized block design,the interaction effect between the block and treatment factors cannot be separated from the error term.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
16
Experimental data are collected so that the values of the dependent variables are set before the values of the independent variable are observed.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
17
In one-way ANOVA,the numerator of the F statistic is an estimate of the population variance based on within-treatment variation.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
18
A one-way analysis of variance is a method that allows us to estimate and compare the effects of several treatments on a response variable.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
19
Different levels of a factor are called ____________.
A)Treatments
B)Variables
C)Responses
D)Observations
A)Treatments
B)Variables
C)Responses
D)Observations

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
20
In a completely randomized (one-way)ANOVA,with other things being equal,as the sample means get closer to each other,the probability of rejecting the null hypothesis decreases.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
21
After analyzing a data set using the one-way ANOVA model,the same data are analyzed using the randomized block design ANOVA model.SS (Treatment)in the one-way ANOVA model is _______________ the SS (Treatment)in the randomized block design ANOVA model.
A)Always equal to
B)Always greater than
C)Always less than
D)Sometimes greater than
A)Always equal to
B)Always greater than
C)Always less than
D)Sometimes greater than

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
22
We have just performed a one-way ANOVA on a given set of data and rejected the null hypothesis for the ANOVA F test.Assume that we are able to perform a randomized block design ANOVA on the same data.For the randomized block design ANOVA,the null hypothesis for equal treatments will __________ be rejected.
A)Always
B)Sometimes
C)Never
A)Always
B)Sometimes
C)Never

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
23
In randomized block ANOVA,the sum of squares for factor 1 equals:
A)SSTO - SS(error)- SS(interaction).
B)SSTO - SS(factor 2)- SSE.
C)SSTO - SS(interaction)- SS(factor 2).
D)SSTO - SS(factor 2).
E)SSTO - SS(error).
A)SSTO - SS(error)- SS(interaction).
B)SSTO - SS(factor 2)- SSE.
C)SSTO - SS(interaction)- SS(factor 2).
D)SSTO - SS(factor 2).
E)SSTO - SS(error).

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
24
___________ simultaneous confidence intervals test all of the pairwise differences between means,respectively,while controlling the overall Type I error.
A)Randomized
B)Tukey
C)Covariate
D)Interacting
A)Randomized
B)Tukey
C)Covariate
D)Interacting

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
25
In a completely randomized ANOVA,with other things equal,as the sample means get closer to each other,the probability of rejecting the null hypothesis:
A)Decreases.
B)Increases.
C)Is unaffected.
A)Decreases.
B)Increases.
C)Is unaffected.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
26
A sum of squares that measures the variability among the sample means is referred to as the:
A)Treatment sum of squares.
B)Error sum of squares.
C)Sum of squares within-treatment.
D)Total sum of squares.
E)Interaction sum of squares.
A)Treatment sum of squares.
B)Error sum of squares.
C)Sum of squares within-treatment.
D)Total sum of squares.
E)Interaction sum of squares.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
27
The F test for testing the difference between means is equal to the ratio of Mean Square _____________ over Mean Square __________________.
A)Treatment,Error
B)Error,Treatment
C)Treatment,Total
D)Error,Total
A)Treatment,Error
B)Error,Treatment
C)Treatment,Total
D)Error,Total

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
28
When computing individual confidence intervals using the t statistic,for all possible pairwise comparisons of means,the experimentwise error rate will be:
A)Equal to α.
B)Less than α.
C)Greater than α.
A)Equal to α.
B)Less than α.
C)Greater than α.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
29
A sum of squares that measures the total amount of variability in the observed values of the response variable is referred to as the:
A)Treatment sum of squares.
B)Error sum of squares.
C)Sum of squares within-treatment.
D)Total sum of squares.
E)Interaction sum of squares.
A)Treatment sum of squares.
B)Error sum of squares.
C)Sum of squares within-treatment.
D)Total sum of squares.
E)Interaction sum of squares.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
30
Which of the following is not an assumption for one-way analysis of variance?
A)The p populations of values of the response variable associated with the treatments have equal variances.
B)The samples of experimental units associated with the treatments are randomly selected.
C)The experimental units associated with the treatments are independent samples.
D)The number of sampled observations must be equal for all p treatments.
E)The distribution of the response variable is normal for all treatments.
A)The p populations of values of the response variable associated with the treatments have equal variances.
B)The samples of experimental units associated with the treatments are randomly selected.
C)The experimental units associated with the treatments are independent samples.
D)The number of sampled observations must be equal for all p treatments.
E)The distribution of the response variable is normal for all treatments.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
31
In one-way ANOVA,the treatment sum of squares equals:
A)SSTO - SS(error)- SS(interaction).
B)SSTO - SS(factor 1)- SSE.
C)SSTO - SS(interaction)- SS(factor 1)- SS(factor 2).
D)SSTO - SS(factor 1)- SS(factor 2).
E)SSTO - SS(error).
A)SSTO - SS(error)- SS(interaction).
B)SSTO - SS(factor 1)- SSE.
C)SSTO - SS(interaction)- SS(factor 1)- SS(factor 2).
D)SSTO - SS(factor 1)- SS(factor 2).
E)SSTO - SS(error).

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
32
In a completely randomized (one-way)analysis of variance problem with c groups and a total of n observations in all groups,the variance between groups is equal to:
A)(Total sum of squares)- (Sum of squares within columns).
B)(Sum of squares between columns)/(c - 1).
C)(Total sum of squares)- [(Sum of squares within columns)/(n - c)].
D)[(Total sum of squares)/(n - 1)] - [(Sum of squares between columns)/(c - 1)].
A)(Total sum of squares)- (Sum of squares within columns).
B)(Sum of squares between columns)/(c - 1).
C)(Total sum of squares)- [(Sum of squares within columns)/(n - c)].
D)[(Total sum of squares)/(n - 1)] - [(Sum of squares between columns)/(c - 1)].

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
33
___________ refers to applying a treatment to more than one experimental unit.
A)Randomization
B)Balanced experiment
C)One-way ANOVA
D)Replication
A)Randomization
B)Balanced experiment
C)One-way ANOVA
D)Replication

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
34
When we compute 100(1 - α)confidence intervals,the value of α is called the
A)Comparisonwise error rate.
B)Tukey simultaneous error rate.
C)Experimentwise error rate.
D)Pairwise error rate.
A)Comparisonwise error rate.
B)Tukey simultaneous error rate.
C)Experimentwise error rate.
D)Pairwise error rate.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
35
When using a completely randomized design (one-way analysis of variance),the calculated F statistic will decrease as:
A)The variability among the groups decreases relative to the variability within the groups.
B)The total variability increases.
C)The total variability decreases.
D)The variability among the groups increases relative to the variability within the groups.
A)The variability among the groups decreases relative to the variability within the groups.
B)The total variability increases.
C)The total variability decreases.
D)The variability among the groups increases relative to the variability within the groups.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
36
Which one of the following is not an assumption of one-way analysis of variance?
A)Random selection of samples from each population.
B)Equality of the population variances.
C)Equality of the population means.
D)Samples selected from each treatment population all have normal distributions.
A)Random selection of samples from each population.
B)Equality of the population variances.
C)Equality of the population means.
D)Samples selected from each treatment population all have normal distributions.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
37
When computing confidence intervals using the Tukey procedure,for all possible pairwise comparisons of means,the experimentwise error rate will be:
A)Equal to α.
B)Less than α.
C)Greater than α.
A)Equal to α.
B)Less than α.
C)Greater than α.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
38
The advantage of the randomized block design over the completely randomized design is that we are comparing the treatments by using ________ experimental units.
A)Randomly selected
B)The same
C)Different
D)Representative
E)Equally timed
A)Randomly selected
B)The same
C)Different
D)Representative
E)Equally timed

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
39
When computing a confidence interval for the difference between two means,the width of the (1 - α)confidence interval based on the Tukey procedure will be __________ the width of the (1 - α)individual confidence interval based on the t statistic.
A)Greater than
B)Less than
C)The same as
D)Sometimes greater than,sometimes less than
A)Greater than
B)Less than
C)The same as
D)Sometimes greater than,sometimes less than

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
40
A ___________ design is an experimental design that compares v treatments by using d blocks,where each block is used exactly once to measure the effect of each treatment.
A)One-way ANOVA
B)Two-way ANOVA
C)Randomized block
D)Balanced complete factorial
A)One-way ANOVA
B)Two-way ANOVA
C)Randomized block
D)Balanced complete factorial

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the one-way ANOVA table. 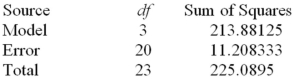 If there are an equal number of observations in each group,then each group (treatment level)consists of how many observations?
If there are an equal number of observations in each group,then each group (treatment level)consists of how many observations?
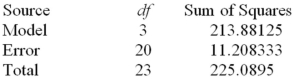 If there are an equal number of observations in each group,then each group (treatment level)consists of how many observations?
If there are an equal number of observations in each group,then each group (treatment level)consists of how many observations?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
42
What is the degrees of freedom error (within-group variation)of a completely randomized design (one-way)ANOVA test with 4 groups and 15 observations per each group?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
43
In one-way ANOVA,the total sum of squares is equal to _______________________.
A)Treatment SS + Error SS
B)Treatment SS - Error SS
C)Treatment SS × Error SS
D)Treatment SS/Error SS
A)Treatment SS + Error SS
B)Treatment SS - Error SS
C)Treatment SS × Error SS
D)Treatment SS/Error SS

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
44
Consider the one-way ANOVA table. 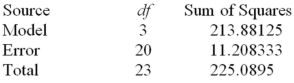 What is the treatment mean square?
What is the treatment mean square?
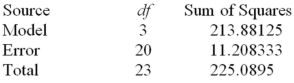 What is the treatment mean square?
What is the treatment mean square?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
45
In general,a Tukey simultaneous 100(1 - α)percent confidence interval is _________ than the corresponding individual 100(1 - α)percent confidence interval.
A)Wider
B)Narrower
C)No different
D)Two times more
A)Wider
B)Narrower
C)No different
D)Two times more

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
46
The variable of interest in an experiment is referred to as the __________ variable.
A)Categorical
B)Regression
C)Response
D)Factor
A)Categorical
B)Regression
C)Response
D)Factor

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
47
In performing a one-way ANOVA,the _________ is the between-group variance.
A)MS Error
B)MS Treatment
C)SS Error
D)SS Treatment
A)MS Error
B)MS Treatment
C)SS Error
D)SS Treatment

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
48
In performing a one-way ANOVA,_________ measures the variability of the observed values around their respective means by summing the squared differences between each observed value of the response and its corresponding treatment mean.
A)SS Error
B)SS Treatment
C)SS Total
D)SS Treatment/SS Error
A)SS Error
B)SS Treatment
C)SS Total
D)SS Treatment/SS Error

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the one-way ANOVA table. 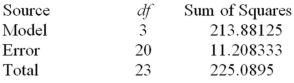 How many groups (treatment levels)are included in the study?
How many groups (treatment levels)are included in the study?
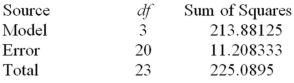 How many groups (treatment levels)are included in the study?
How many groups (treatment levels)are included in the study?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
50
If the total sum of squares in a one-way analysis of variance is 25 and the treatment sum of squares is 17,then what is the error sum of squares?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
51
In a one way ANOVA table,the ___________ the value of MSE,the higher the probability of rejecting the hypothesis that all treatment means are equal.
A)Closer to 1
B)Closer to 0
C)Larger
D)Smaller
A)Closer to 1
B)Closer to 0
C)Larger
D)Smaller

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
52
In a ___________________ experimental design,independent random samples of experimental units are assigned to the treatments.
A)One-way ANOVA
B)Two-way ANOVA
C)Randomized block
D)Balanced complete factorial
A)One-way ANOVA
B)Two-way ANOVA
C)Randomized block
D)Balanced complete factorial

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
53
Looking at four different diets,a researcher randomly assigned 20 equally overweight women into each of the four diets.What are the degrees of freedom for the treatments?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
54
The ___________________ units are the entities (objects,people,etc. )to which the treatments are assigned.
A)Variable
B)Block
C)Experimental
D)Random
A)Variable
B)Block
C)Experimental
D)Random

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the one-way ANOVA table. 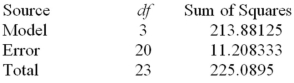 What is the mean square error?
What is the mean square error?
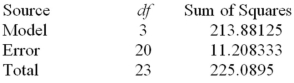 What is the mean square error?
What is the mean square error?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
56
What is the degrees of freedom treatment (between-group variation)of a completely randomized design (one-way)ANOVA test with 4 groups and 15 observations per each group?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
57
What is the degrees of freedom error for a randomized block design ANOVA test with 4 treatments and 5 blocks?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
58
In a one-way analysis of variance with three treatments,each with five measurements,in which a completely randomized design is used,what is the degrees of freedom for treatments?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
59
The dependent variable,the variable of interest in an experiment,is also called the ___________ variable.
A)Categorical
B)Regression
C)Response
D)Factor
A)Categorical
B)Regression
C)Response
D)Factor

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
60
In a one-way analysis of variance with three treatments,each with five measurements,in which a completely randomized design is used,what is the degrees of freedom for error?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
61
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. 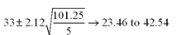 Compute a 95 percent confidence interval for the first treatment mean.
Compute a 95 percent confidence interval for the first treatment mean.
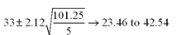 Compute a 95 percent confidence interval for the first treatment mean.
Compute a 95 percent confidence interval for the first treatment mean.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
62
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 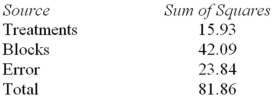 Test H0: There is no difference between treatment effects at α = .05.
Test H0: There is no difference between treatment effects at α = .05.
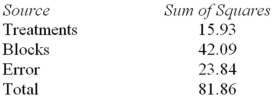 Test H0: There is no difference between treatment effects at α = .05.
Test H0: There is no difference between treatment effects at α = .05.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
63
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 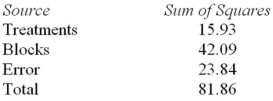 What is the mean square error?
What is the mean square error?
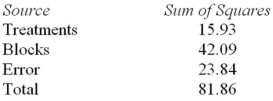 What is the mean square error?
What is the mean square error?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
64
In a one-way analysis of variance with three treatments,each with five measurements,in which a completely randomized design is used,compute the F statistic where the sum of squares treatment is 17.0493 and the sum of squares error is 8.028.

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 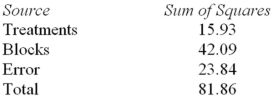 Determine the degrees of freedom for treatments.
Determine the degrees of freedom for treatments.
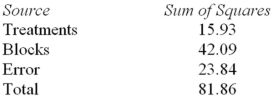 Determine the degrees of freedom for treatments.
Determine the degrees of freedom for treatments.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 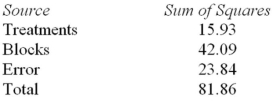 Determine the degrees of freedom for error.
Determine the degrees of freedom for error.
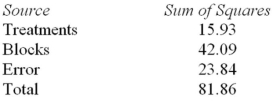 Determine the degrees of freedom for error.
Determine the degrees of freedom for error.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations.The response variable is sales in millions of dollars and four treatment levels represent the four regions that the company serves. 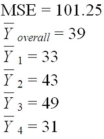 Perform a pairwise comparison between treatment mean 1 and treatment mean 4 by computing a Tukey 95 percent simultaneous confidence interval.
Perform a pairwise comparison between treatment mean 1 and treatment mean 4 by computing a Tukey 95 percent simultaneous confidence interval.
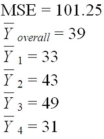 Perform a pairwise comparison between treatment mean 1 and treatment mean 4 by computing a Tukey 95 percent simultaneous confidence interval.
Perform a pairwise comparison between treatment mean 1 and treatment mean 4 by computing a Tukey 95 percent simultaneous confidence interval.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
68
Find a Tukey simultaneous 95 percent confidence interval for μC - μB,where 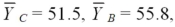 and MSE = 6.125.There were 4 treatments and 24 observations total,and the number of observations were equal in each group.
and MSE = 6.125.There were 4 treatments and 24 observations total,and the number of observations were equal in each group.
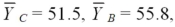 and MSE = 6.125.There were 4 treatments and 24 observations total,and the number of observations were equal in each group.
and MSE = 6.125.There were 4 treatments and 24 observations total,and the number of observations were equal in each group.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
69
Find a Tukey simultaneous 95 percent confidence interval for μ1 - μ2,where 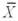 1 = 33.98,
1 = 33.98, 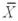 2 = 36.56,and MSE = 0.669.There were 15 observations total and 3 treatments.Assume that the number of observations in each treatment is equal.
2 = 36.56,and MSE = 0.669.There were 15 observations total and 3 treatments.Assume that the number of observations in each treatment is equal.
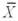 1 = 33.98,
1 = 33.98, 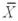 2 = 36.56,and MSE = 0.669.There were 15 observations total and 3 treatments.Assume that the number of observations in each treatment is equal.
2 = 36.56,and MSE = 0.669.There were 15 observations total and 3 treatments.Assume that the number of observations in each treatment is equal.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 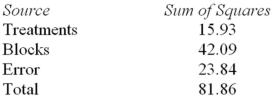 What is the block mean square?
What is the block mean square?
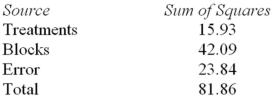 What is the block mean square?
What is the block mean square?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 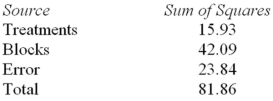 What is the calculated F statistic for treatments?
What is the calculated F statistic for treatments?
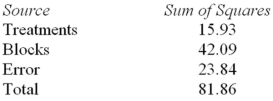 What is the calculated F statistic for treatments?
What is the calculated F statistic for treatments?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
72
Looking at four different diets,a researcher randomly assigned 20 equally overweight women into each of the four diets.What are the degrees of freedom total?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the following one-way ANOVA table. 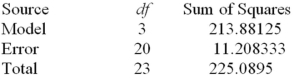 What is the value of the F statistic?
What is the value of the F statistic?
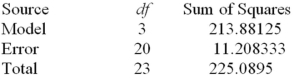 What is the value of the F statistic?
What is the value of the F statistic?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
74
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations.The response variable is sales in millions of dollars,and the four treatment levels represent the four regions that the company serves. 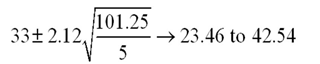 Perform a pairwise comparison between treatment mean 3 and treatment mean 4 by computing a Tukey 90 percent simultaneous confidence interval.
Perform a pairwise comparison between treatment mean 3 and treatment mean 4 by computing a Tukey 90 percent simultaneous confidence interval.
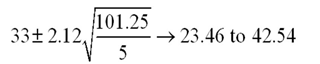 Perform a pairwise comparison between treatment mean 3 and treatment mean 4 by computing a Tukey 90 percent simultaneous confidence interval.
Perform a pairwise comparison between treatment mean 3 and treatment mean 4 by computing a Tukey 90 percent simultaneous confidence interval.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
75
Looking at four different diets,a researcher randomly assigned 20 equally overweight women into each of the four diets.What are the degrees of freedom for the individual confidence intervals?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 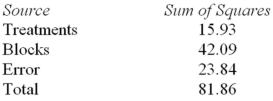 Calculate the degrees of freedom for blocks.
Calculate the degrees of freedom for blocks.
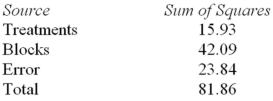 Calculate the degrees of freedom for blocks.
Calculate the degrees of freedom for blocks.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
77
Looking at four different diets,a researcher randomly assigned 20 equally overweight women into each of the four diets.What are the degrees of freedom for the error?

Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 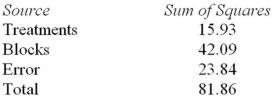 What is the treatment mean square?
What is the treatment mean square?
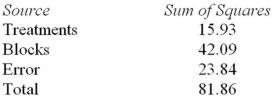 What is the treatment mean square?
What is the treatment mean square?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
79
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. 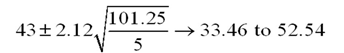 Compute a 95 percent confidence interval for the second treatment mean.
Compute a 95 percent confidence interval for the second treatment mean.
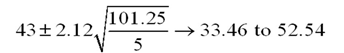 Compute a 95 percent confidence interval for the second treatment mean.
Compute a 95 percent confidence interval for the second treatment mean.
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments. 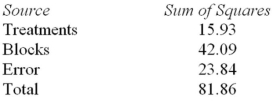 What is the calculated F statistic for blocks?
What is the calculated F statistic for blocks?
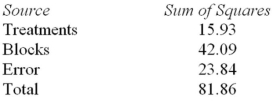 What is the calculated F statistic for blocks?
What is the calculated F statistic for blocks?
Unlock Deck
Unlock for access to all 98 flashcards in this deck.
Unlock Deck
k this deck


