Deck 8: Interval Estimation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/137
Play
Full screen (f)
Deck 8: Interval Estimation
1
In order to use the normal distribution for interval estimation of when is known and the sample is very small, the population
A)must be very large
B)must have a normal distribution
C)can have any distribution
D)must have a mean of at least 1
A)must be very large
B)must have a normal distribution
C)can have any distribution
D)must have a mean of at least 1
must have a normal distribution
2
As the number of degrees of freedom for a t distribution increases, the difference between the t distribution and the standard normal distribution
A)becomes larger
B)becomes smaller
C)stays the same
D)None of these alternatives is correct.
A)becomes larger
B)becomes smaller
C)stays the same
D)None of these alternatives is correct.
becomes smaller
3
The value added and subtracted from a point estimate in order to develop an interval estimate of the population parameter is known as the
A)confidence level
B)margin of error
C)parameter estimate
D)interval estimate
A)confidence level
B)margin of error
C)parameter estimate
D)interval estimate
margin of error
4
If we want to provide a 95% confidence interval for the mean of a population, the confidence coefficient is
A)0.485
B)1.96
C)0.95
D)1.645
A)0.485
B)1.96
C)0.95
D)1.645

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
5
A population has a standard deviation of 50. A random sample of 100 items from this population is selected. The sample mean is determined to be 600. At 95% confidence, the margin of error is
A)5
B)9.8
C)650
D)609.8
A)5
B)9.8
C)650
D)609.8

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
6
If an interval estimate is said to be constructed at the 90% confidence level, the confidence coefficient would be
A)0.1
B)0.95
C)0.9
D)0.05
A)0.1
B)0.95
C)0.9
D)0.05

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
7
From a population that is not normally distributed and whose standard deviation is not known, a sample of 6 items is selected to develop an interval estimate for the mean of the population ( ).
A)The normal distribution can be used.
B)The t distribution with 5 degrees of freedom must be used.
C)The t distribution with 6 degrees of freedom must be used.
D)The sample size must be increased.
A)The normal distribution can be used.
B)The t distribution with 5 degrees of freedom must be used.
C)The t distribution with 6 degrees of freedom must be used.
D)The sample size must be increased.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
8
In interval estimation, the t distribution is applicable only when
A)the population has a mean of less than 30
B)the sample standard deviation is used to estimate the population standard deviation
C)the variance of the population is known
D)the standard deviation of the population is known
A)the population has a mean of less than 30
B)the sample standard deviation is used to estimate the population standard deviation
C)the variance of the population is known
D)the standard deviation of the population is known

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
9
In interval estimation, as the sample size becomes larger, the interval estimate
A)becomes narrower
B)becomes wider
C)remains the same, since the mean is not changing
D)gets closer to 1.96
A)becomes narrower
B)becomes wider
C)remains the same, since the mean is not changing
D)gets closer to 1.96

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
10
In an interval estimation for a proportion of a population, the critical value of Z at 99.2% confidence is
A)2.65
B)2.44
C)1.96
D)1.645
A)2.65
B)2.44
C)1.96
D)1.645

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
11
In developing an interval estimate, if the population standard deviation is unknown
A)it is impossible to develop an interval estimate
B)the standard deviation is arrived at using the range
C)the sample standard deviation can be used
D)it is assumed that the population standard deviation is 1
A)it is impossible to develop an interval estimate
B)the standard deviation is arrived at using the range
C)the sample standard deviation can be used
D)it is assumed that the population standard deviation is 1

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
12
Whenever the population standard deviation is unknown and the population has a normal or near-normal distribution, which distribution is used in developing an interval estimation?
A)standard distribution
B)z distribution
C)alpha distribution
D)t distribution
A)standard distribution
B)z distribution
C)alpha distribution
D)t distribution

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
13
In order to determine an interval for the mean of a population with unknown standard deviation a sample of 61 items is selected. The mean of the sample is determined to be 23. The number of degrees of freedom for reading the t value is
A)22
B)23
C)60
D)61
A)22
B)23
C)60
D)61

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
14
An estimate of a population parameter that provides an interval of values believed to contain the value of the parameter is known as the
A)confidence level
B)interval estimate
C)parameter value
D)population estimate
A)confidence level
B)interval estimate
C)parameter value
D)population estimate

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
15
From a population with a variance of 900, a sample of 225 items is selected. At 95% confidence, the margin of error is
A)15
B)2
C)3.92
D)4
A)15
B)2
C)3.92
D)4

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
16
When "S" is used to estimate " ," the margin of error is computed by using
A)normal distribution
B)t distribution
C)the mean of the sample
D)the mean of the population
A)normal distribution
B)t distribution
C)the mean of the sample
D)the mean of the population

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
17
From a population that is normally distributed, a sample of 25 elements is selected and the standard deviation of the sample is computed. For the interval estimation of , the proper distribution to use is the
A)normal distribution
B)t distribution with 25 degrees of freedom
C)t distribution with 26 degrees of freedom
D)t distribution with 24 degrees of freedom
A)normal distribution
B)t distribution with 25 degrees of freedom
C)t distribution with 26 degrees of freedom
D)t distribution with 24 degrees of freedom

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
18
A sample of 200 elements from a population with a known standard deviation is selected. For an interval estimation of , the proper distribution to use is the
A)normal distribution
B)t distribution with 200 degrees of freedom
C)t distribution with 201 degrees of freedom
D)t distribution with 202 degrees of freedom
A)normal distribution
B)t distribution with 200 degrees of freedom
C)t distribution with 201 degrees of freedom
D)t distribution with 202 degrees of freedom

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
19
For the interval estimation of when is known and the sample is large, the proper distribution to use is
A)the normal distribution
B)the t distribution with n degrees of freedom
C)the t distribution with n + 1 degrees of freedom
D)the t distribution with n + 2 degrees of freedom
A)the normal distribution
B)the t distribution with n degrees of freedom
C)the t distribution with n + 1 degrees of freedom
D)the t distribution with n + 2 degrees of freedom

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
20
The absolute value of the difference between the point estimate and the population parameter it estimates is
A)the standard error
B)the sampling error
C)precision
D)the error of confidence
A)the standard error
B)the sampling error
C)precision
D)the error of confidence

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
21
When the level of confidence decreases, the margin of error
A)stays the same
B)becomes smaller
C)becomes larger
D)becomes smaller or larger, depending on the sample size
A)stays the same
B)becomes smaller
C)becomes larger
D)becomes smaller or larger, depending on the sample size

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
22
In general, higher confidence levels provide
A)wider confidence intervals
B)narrower confidence intervals
C)a smaller standard error
D)unbiased estimates
A)wider confidence intervals
B)narrower confidence intervals
C)a smaller standard error
D)unbiased estimates

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
23
Whenever using the t distribution for interval estimation (when the sample size is very small), we must assume that
A)the sample has a mean of at least 30
B)the sampling distribution is not normal
C)the population is approximately normal
D)the finite population correction factor is necessary
A)the sample has a mean of at least 30
B)the sampling distribution is not normal
C)the population is approximately normal
D)the finite population correction factor is necessary

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
24
A 95% confidence interval for a population mean is determined to be 100 to 120. If the confidence coefficient is reduced to 0.90, the interval for
A)becomes narrower
B)becomes wider
C)does not change
D)becomes 0.1
A)becomes narrower
B)becomes wider
C)does not change
D)becomes 0.1

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
25
A random sample of 64 students at a university showed an average age of 25 years and a sample standard deviation of 2 years. The 98% confidence interval for the true average age of all students in the university is
A)20.5 to 26.5
B)24.4 to 25.6
C)23.0 to 27.0
D)20.0 to 30.0
A)20.5 to 26.5
B)24.4 to 25.6
C)23.0 to 27.0
D)20.0 to 30.0

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
26
If we change a 95% confidence interval estimate to a 99% confidence interval estimate, we can expect
A)the size of the confidence interval to increase
B)the size of the confidence interval to decrease
C)the size of the confidence interval to remain the same
D)the sample size to increase
A)the size of the confidence interval to increase
B)the size of the confidence interval to decrease
C)the size of the confidence interval to remain the same
D)the sample size to increase

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
27
A random sample of 144 observations has a mean of 20, a median of 21, and a mode of 22. The population standard deviation is known to equal 4.8. The 95.44% confidence interval for the population mean is
A)15.2 to 24.8
B)19.200 to 20.800
C)19.216 to 20.784
D)21.2 to 22.8
A)15.2 to 24.8
B)19.200 to 20.800
C)19.216 to 20.784
D)21.2 to 22.8

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
28
A sample of 20 items from a population with an unknown is selected in order to develop an interval estimate of . Which of the following is not necessary?
A)We must assume the population has a normal distribution.
B)We must use a t distribution.
C)Sample standard deviation must be used to estimate .
D)The sample must have a normal distribution.
A)We must assume the population has a normal distribution.
B)We must use a t distribution.
C)Sample standard deviation must be used to estimate .
D)The sample must have a normal distribution.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
29
The ability of an interval estimate to contain the value of the population parameter is described by the
A)confidence level
B)degrees of freedom
C)precise value of the population mean
D)degrees of freedom minus 1
A)confidence level
B)degrees of freedom
C)precise value of the population mean
D)degrees of freedom minus 1

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
30
It is known that the variance of a population equals 1,936. A random sample of 121 has been taken from the population. There is a .95 probability that the sample mean will provide a margin of error of
A)7.84
B)31.36
C)344.96
D)1,936
A)7.84
B)31.36
C)344.96
D)1,936

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
31
For which of the following values of P is the value of P(1 - P) maximized?
A)P = 0.99
B)P = 0.90
C)P = 0.01
D)P = 0.50
A)P = 0.99
B)P = 0.90
C)P = 0.01
D)P = 0.50

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
32
A sample of 225 elements from a population with a standard deviation of 75 is selected. The sample mean is 180. The 95% confidence interval for is
A)105.0 to 225.0
B)175.0 to 185.0
C)100.0 to 200.0
D)170.2 to 189.8
A)105.0 to 225.0
B)175.0 to 185.0
C)100.0 to 200.0
D)170.2 to 189.8

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
33
Using an = 0.04 a confidence interval for a population proportion is determined to be 0.65 to 0.75. If the level of significance is decreased, the interval for the population proportion
A)becomes narrower
B)becomes wider
C)does not change
D)remains the same
A)becomes narrower
B)becomes wider
C)does not change
D)remains the same

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
34
As the sample size increases, the margin of error
A)increases
B)decreases
C)stays the same
D)increases or decreases depending on the size of the mean
A)increases
B)decreases
C)stays the same
D)increases or decreases depending on the size of the mean

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
35
An interval estimate is a range of values used to estimate
A)the shape of the population's distribution
B)the sampling distribution
C)a sample statistic
D)a population parameter
A)the shape of the population's distribution
B)the sampling distribution
C)a sample statistic
D)a population parameter

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
36
In determining the sample size necessary to estimate a population proportion, which of the following information is not needed?
A)the maximum margin of error that can be tolerated
B)the confidence level required
C)a preliminary estimate of the true population proportion P
D)the mean of the population
A)the maximum margin of error that can be tolerated
B)the confidence level required
C)a preliminary estimate of the true population proportion P
D)the mean of the population

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
37
The z value for a 97.8% confidence interval estimation is
A)2.02
B)1.96
C)2.00
D)2.29
A)2.02
B)1.96
C)2.00
D)2.29

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
38
The t value for a 95% confidence interval estimation with 24 degrees of freedom is
A)1.711
B)2.064
C)2.492
D)2.069
A)1.711
B)2.064
C)2.492
D)2.069

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
39
A random sample of 49 statistics examinations was taken. The average score, in the sample, was 84 with a variance of 12.25. The 95% confidence interval for the average examination score of the population of the examinations is
A)76.00 to 84.00
B)77.40 to 86.60
C)83.00 to 85.00
D)68.00 to 100.00
A)76.00 to 84.00
B)77.40 to 86.60
C)83.00 to 85.00
D)68.00 to 100.00

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
40
After computing a confidence interval, the user believes the results are meaningless because the width of the interval is too large. Which one of the following is the best recommendation?
A)Increase the level of confidence for the interval.
B)Decrease the sample size.
C)Increase the sample size.
D)Reduce the population variance.
A)Increase the level of confidence for the interval.
B)Decrease the sample size.
C)Increase the sample size.
D)Reduce the population variance.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
41
Exhibit 8-2
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
-Refer to Exhibit 8-2. The 96.6% confidence interval for is
A)63.00 to 67.00
B)60.76 to 69.24
C)61.08 to 68.92
D)60.00 to 80.00
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
-Refer to Exhibit 8-2. The 96.6% confidence interval for is
A)63.00 to 67.00
B)60.76 to 69.24
C)61.08 to 68.92
D)60.00 to 80.00

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
42
It is known that the population variance equals 484. With a 0.95 probability, the sample size that needs to be taken if the desired margin of error is 5 or less is
A)25
B)74
C)189
D)75
A)25
B)74
C)189
D)75

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
43
Which of the following best describes the form of the sampling distribution of the sample proportion?
A)When standardized, it is exactly the standard normal distribution.
B)When standardized, it is the t distribution.
C)It is approximately normal as long as n 30.
30.
D)It is approximately normal as long as np 5 and n(1-p)
5 and n(1-p)  5.
5.
A)When standardized, it is exactly the standard normal distribution.
B)When standardized, it is the t distribution.
C)It is approximately normal as long as n
 30.
30.D)It is approximately normal as long as np
 5 and n(1-p)
5 and n(1-p)  5.
5.
Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
44
In a random sample of 144 observations, 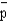 = 0.6. The 95% confidence interval for P is
= 0.6. The 95% confidence interval for P is
A)0.52 to 0.68
B)0.144 to 0.200
C)0.60 to 0.70
D)0.50 to 0.70
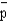 = 0.6. The 95% confidence interval for P is
= 0.6. The 95% confidence interval for P isA)0.52 to 0.68
B)0.144 to 0.200
C)0.60 to 0.70
D)0.50 to 0.70

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
45
When constructing a confidence interval for the population mean and the standard deviation of the sample is used, the degrees of freedom for the t distribution equals
A)n-1
B)n
C)29
D)30
A)n-1
B)n
C)29
D)30

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
46
A random sample of 1000 people was taken. Four hundred fifty of the people in the sample favored Candidate A. The 95% confidence interval for the true proportion of people who favors Candidate A is
A)0.419 to 0.481
B)0.40 to 0.50
C)0.45 to 0.55
D)1.645 to 1.96
A)0.419 to 0.481
B)0.40 to 0.50
C)0.45 to 0.55
D)1.645 to 1.96

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
47
Exhibit 8-1
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours.
Refer to Exhibit 8-1. The standard error of the mean is
A)7.50
B)0.39
C)2.00
D)0.20
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours.
Refer to Exhibit 8-1. The standard error of the mean is
A)7.50
B)0.39
C)2.00
D)0.20

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
48
In a random sample of 100 observations, 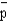 = 0.2. The 95.44% confidence interval for P is
= 0.2. The 95.44% confidence interval for P is
A)0.122 to 0.278
B)0.164 to 0.236
C)0.134 to 0.266
D)0.120 to 0.280
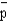 = 0.2. The 95.44% confidence interval for P is
= 0.2. The 95.44% confidence interval for P isA)0.122 to 0.278
B)0.164 to 0.236
C)0.134 to 0.266
D)0.120 to 0.280

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
49
Exhibit 8-2
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
-Refer to Exhibit 8-2. If the sample size was 100 (other factors remain unchanged), the interval for would
A)not change
B)become narrower
C)become wider
D)become zero
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
-Refer to Exhibit 8-2. If the sample size was 100 (other factors remain unchanged), the interval for would
A)not change
B)become narrower
C)become wider
D)become zero

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
50
A machine that produces a major part for an airplane engine is monitored closely. In the past, 10% of the parts produced would be defective. With a .95 probability, the sample size that needs to be taken if the desired margin of error is .04 or less is
A)110
B)111
C)216
D)217
A)110
B)111
C)216
D)217

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
51
The following random sample from a population whose values were normally distributed was collected.10 8 11 11
The 95% confidence interval for is
A)8.52 to 10.98
B)7.75 to 12.25
C)9.75 to 10.75
D)8.00 to 10.00
The 95% confidence interval for is
A)8.52 to 10.98
B)7.75 to 12.25
C)9.75 to 10.75
D)8.00 to 10.00

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
52
Exhibit 8-2
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
Refer to Exhibit 8-2. The standard error of the mean is
A)22.00
B)96.60
C)4.24
D)2.00
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
Refer to Exhibit 8-2. The standard error of the mean is
A)22.00
B)96.60
C)4.24
D)2.00

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
53
In a sample of 400 voters, 360 indicated they favor the incumbent governor. The 95% confidence interval of voters not favoring the incumbent is
A)0.871 to 0.929
B)0.120 to 0.280
C)0.765 to 0.835
D)0.071 to 0.129
A)0.871 to 0.929
B)0.120 to 0.280
C)0.765 to 0.835
D)0.071 to 0.129

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
54
Exhibit 8-2
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
Refer to Exhibit 8-2. If the confidence coefficient is reduced to 0.9, the standard error of the mean
A)will increase
B)will decrease
C)remains unchanged
D)becomes negative
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
Refer to Exhibit 8-2. If the confidence coefficient is reduced to 0.9, the standard error of the mean
A)will increase
B)will decrease
C)remains unchanged
D)becomes negative

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
55
We are interested in conducting a study in order to determine what percentage of voters of a state would vote for the incumbent governor. What is the minimum size sample needed to estimate the population proportion with a margin of error of 0.05 or less at 95% confidence?
A)200
B)100
C)58
D)385
A)200
B)100
C)58
D)385

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
56
The following random sample from a population whose values were normally distributed was collected.10 12 18 16
The 80% confidence interval for is
A)12.054 to 15.946
B)10.108 to 17.892
C)10.321 to 17.679
D)11.009 to 16.991
The 80% confidence interval for is
A)12.054 to 15.946
B)10.108 to 17.892
C)10.321 to 17.679
D)11.009 to 16.991

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
57
The sample size needed to provide a margin of error of 2 or less with a .95 probability when the population standard deviation equals 11 is
A)10
B)11
C)116
D)117
A)10
B)11
C)116
D)117

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
58
Exhibit 8-2
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
-Refer to Exhibit 8-2. If we are interested in determining an interval estimate for at 96.6% confidence, the Z value to use is
A)1.96
B)0.483
C)2.12
D)1.645
A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph.
-Refer to Exhibit 8-2. If we are interested in determining an interval estimate for at 96.6% confidence, the Z value to use is
A)1.96
B)0.483
C)2.12
D)1.645

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
59
Exhibit 8-1
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours.
Refer to Exhibit 8-1. With a 0.95 probability, the margin of error is approximately
A)0.39
B)1.96
C)0.20
D)1.64
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours.
Refer to Exhibit 8-1. With a 0.95 probability, the margin of error is approximately
A)0.39
B)1.96
C)0.20
D)1.64

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
60
Exhibit 8-1
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours.
Refer to Exhibit 8-1. If the sample mean is 9 hours, then the 95% confidence interval is
A)7.04 to 110.96 hours
B)7.36 to 10.64 hours
C)7.80 to 10.20 hours
D)8.61 to 9.39 hours
In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours.
Refer to Exhibit 8-1. If the sample mean is 9 hours, then the 95% confidence interval is
A)7.04 to 110.96 hours
B)7.36 to 10.64 hours
C)7.80 to 10.20 hours
D)8.61 to 9.39 hours

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
61
Exhibit 8-5
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. The "t" value for this interval estimation is
A)1.96
B)1.998
C)1.64
D)1.28
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. The "t" value for this interval estimation is
A)1.96
B)1.998
C)1.64
D)1.28

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
62
Exhibit 8-6
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. The value of the margin of error at 95% confidence is
A)80.83
B)7
C)0.8083
D)1.611
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. The value of the margin of error at 95% confidence is
A)80.83
B)7
C)0.8083
D)1.611

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
63
A random sample of 81 credit sales in a department store showed an average sale of $68.00. From past data, it is known that the standard deviation of the population is $27.00.
a.Determine the standard error of the mean.
b.With a 0.95 probability, what can be said about the size of the margin of error?
c.What is the 95% confidence interval of the population mean?
a.Determine the standard error of the mean.
b.With a 0.95 probability, what can be said about the size of the margin of error?
c.What is the 95% confidence interval of the population mean?

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
64
Exhibit 8-4
In order to estimate the average electric usage per month, a sample of 81 houses was selected, and the electric usage was determined. Assume a population standard deviation of 450-kilowatt hours.
Refer to Exhibit 8-4. The standard error of the mean is
A)450
B)81
C)500
D)50
In order to estimate the average electric usage per month, a sample of 81 houses was selected, and the electric usage was determined. Assume a population standard deviation of 450-kilowatt hours.
Refer to Exhibit 8-4. The standard error of the mean is
A)450
B)81
C)500
D)50

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
65
In a sample of 400 registered voters, 204 were Democrats.
a.Provide a 95% confidence for the proportion of registered Democrats voters in the population.
b.There are 169 million registered voters in the US. Determine an interval for the number (how many) of registered Democrats in the population.
a.Provide a 95% confidence for the proportion of registered Democrats voters in the population.
b.There are 169 million registered voters in the US. Determine an interval for the number (how many) of registered Democrats in the population.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
66
Exhibit 8-6
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. The 95% confidence interval for the average hourly wage of all information system managers is
A)40.75 to 42.36
B)39.14 to 40.75
C)39.14 to 42.36
D)30 to 50
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. The 95% confidence interval for the average hourly wage of all information system managers is
A)40.75 to 42.36
B)39.14 to 40.75
C)39.14 to 42.36
D)30 to 50

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
67
Exhibit 8-5
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. The 95% confidence interval for the SAT scores is
A)1340.05 to 1459.95
B)1400 to 1459.95
C)1340.05 to 1400
D)1400 to 1600
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. The 95% confidence interval for the SAT scores is
A)1340.05 to 1459.95
B)1400 to 1459.95
C)1340.05 to 1400
D)1400 to 1600

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
68
Exhibit 8-5
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. If we want to provide a 95% confidence interval for the SAT scores, the degrees of freedom for reading the critical values of "t" statistic is
A)60
B)61
C)62
D)63
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. If we want to provide a 95% confidence interval for the SAT scores, the degrees of freedom for reading the critical values of "t" statistic is
A)60
B)61
C)62
D)63

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
69
Exhibit 8-6
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. The standard error of the mean is
A)80.83
B)7
C)0.8083
D)1.611
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. The standard error of the mean is
A)80.83
B)7
C)0.8083
D)1.611

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
70
A random sample of 87 airline pilots had an average yearly income of $99,400 with a standard deviation of $12,000.
a.If we want to determine a 95% confidence interval for the average yearly income, what is the value of t?
b.Develop a 95% confidence interval for the average yearly income of all pilots.
a.If we want to determine a 95% confidence interval for the average yearly income, what is the value of t?
b.Develop a 95% confidence interval for the average yearly income of all pilots.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
71
Exhibit 8-5
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. The margin of error at 95% confidence is
A)1.998
B)1400
C)240
D)59.95
A random sample of 64 SAT scores of students applying for merit scholarships showed an average of 1400 with a standard deviation of 240.
Refer to Exhibit 8-5. The margin of error at 95% confidence is
A)1.998
B)1400
C)240
D)59.95

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
72
Exhibit 8-3
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the population of checkout times is one minute.
Refer to Exhibit 8-3. The standard error of the mean equals
A)0.001
B)0.010
C)0.100
D)1.000
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the population of checkout times is one minute.
Refer to Exhibit 8-3. The standard error of the mean equals
A)0.001
B)0.010
C)0.100
D)1.000

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
73
Exhibit 8-4
In order to estimate the average electric usage per month, a sample of 81 houses was selected, and the electric usage was determined. Assume a population standard deviation of 450-kilowatt hours.
Refer to Exhibit 8-4. If the sample mean is 1,858 KWH, the 95% confidence interval estimate of the population mean is
A)1,760 to 1,956 KWH
B)1,858 to 1,956 KWH
C)1,760 to 1,858 KWH
D)none of these alternatives is correct
In order to estimate the average electric usage per month, a sample of 81 houses was selected, and the electric usage was determined. Assume a population standard deviation of 450-kilowatt hours.
Refer to Exhibit 8-4. If the sample mean is 1,858 KWH, the 95% confidence interval estimate of the population mean is
A)1,760 to 1,956 KWH
B)1,858 to 1,956 KWH
C)1,760 to 1,858 KWH
D)none of these alternatives is correct

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
74
Exhibit 8-6
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. If we want to determine a 95% confidence interval for the average hourly income, the value of "t" statistics is
A)1.96
B)1.64
C)1.28
D)1.993
A sample of 75 information system managers had an average hourly income of $40.75 with a standard deviation of $7.00.
Refer to Exhibit 8-6. If we want to determine a 95% confidence interval for the average hourly income, the value of "t" statistics is
A)1.96
B)1.64
C)1.28
D)1.993

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
75
Exhibit 8-4
In order to estimate the average electric usage per month, a sample of 81 houses was selected, and the electric usage was determined. Assume a population standard deviation of 450-kilowatt hours.
Refer to Exhibit 8-4. At 95% confidence, the size of the margin of error is
A)1.96
B)50
C)98
D)42
In order to estimate the average electric usage per month, a sample of 81 houses was selected, and the electric usage was determined. Assume a population standard deviation of 450-kilowatt hours.
Refer to Exhibit 8-4. At 95% confidence, the size of the margin of error is
A)1.96
B)50
C)98
D)42

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
76
A sample of 196 bags of sugar produced by Domain sugar producers showed an average of 2 pounds and 2 ounces with a standard deviation of 7 ounces.
a.At 95% confidence, compute the margin of error and explain what it shows.
b.Determine a 95% confidence interval for the weight of the population of bags of sugar produced by the company. Give the answer in ounces and at least two significant digits.
c.The bags of sugar produced are supposed to contain 2 pounds of sugar, but the company allows 2% higher or lower than the 2 pounds. Have they reached their desired goal? Explain why or why not by giving numerical facts.
a.At 95% confidence, compute the margin of error and explain what it shows.
b.Determine a 95% confidence interval for the weight of the population of bags of sugar produced by the company. Give the answer in ounces and at least two significant digits.
c.The bags of sugar produced are supposed to contain 2 pounds of sugar, but the company allows 2% higher or lower than the 2 pounds. Have they reached their desired goal? Explain why or why not by giving numerical facts.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
77
A sample of 144 commuters in Boston indicated that they commute an average of one hour and thirty minutes per day. The standard deviation of the sample was 36 minutes. Compute the 95% confidence interval for the average commute time of the population (in minutes).

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
78
Exhibit 8-3
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the population of checkout times is one minute.
Refer to Exhibit 8-3. The 95% confidence interval for the true average checkout time (in minutes) is
A)3:00 to 5:00
B)1.36 to 4.64
C)1.00 to 5.00
D)2.804 to 3.196
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the population of checkout times is one minute.
Refer to Exhibit 8-3. The 95% confidence interval for the true average checkout time (in minutes) is
A)3:00 to 5:00
B)1.36 to 4.64
C)1.00 to 5.00
D)2.804 to 3.196

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
79
A local university administers a comprehensive examination to the candidates for B.S. degrees in Business Administration. Five examinations are selected at random and scored. The scores are shown below. 
a.Compute the mean and the standard deviation of the sample.
b.Compute the margin of error at 95% confidence.
c.Develop a 95% confidence interval estimate for the mean of the population. Assume the population is normally distributed.

a.Compute the mean and the standard deviation of the sample.
b.Compute the margin of error at 95% confidence.
c.Develop a 95% confidence interval estimate for the mean of the population. Assume the population is normally distributed.

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck
80
Exhibit 8-3
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the population of checkout times is one minute.
Refer to Exhibit 8-3. With a .95 probability, the sample mean will provide a margin of error of
A)1.96
B)0.10
C)0.196
D)1.64
The manager of a grocery store has taken a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the population of checkout times is one minute.
Refer to Exhibit 8-3. With a .95 probability, the sample mean will provide a margin of error of
A)1.96
B)0.10
C)0.196
D)1.64

Unlock Deck
Unlock for access to all 137 flashcards in this deck.
Unlock Deck
k this deck


