Deck 2: Nonlinear Functions and Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 2: Nonlinear Functions and Models
1
Find the logistic function f with the given properties. f has limiting value 18 and passes through (0, 9) and (1, 16).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
The chart shows the number of research articles in the prominent journal Physics Review that were written by researchers in Europe during 1983 - 2003 ( represents 1983). 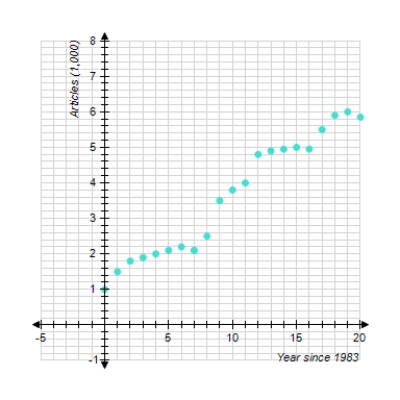
Which of the following logistic functions best models the data (t is the number of years since 1983.) Try to determine the correct model without actually computing data points.
A)
B)
C)
D)
E)

Which of the following logistic functions best models the data (t is the number of years since 1983.) Try to determine the correct model without actually computing data points.
A)
B)
C)
D)
E)
3
There are currently 1,000 cases of Venusian flu in a total susceptible population of 10,000 and the number of cases is increasing by 25% each day. Find a logistic model for the number of cases of Venusian flu and use your model to predict the number of flu cases a week from now. Round your answer to the nearest integer.
A) cases
B) cases
C) cases
D) cases
E) cases
A) cases
B) cases
C) cases
D) cases
E) cases
cases
4
Find N, A, and b for the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Choose the logistic function that best approximates the curve. 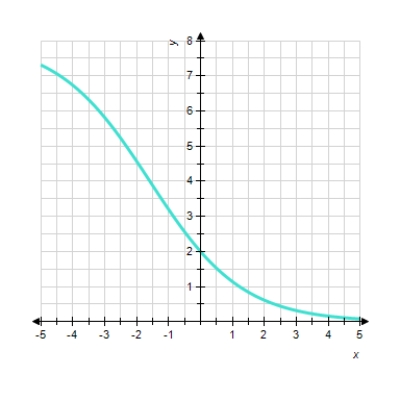
A)
B)
C)

A)
B)
C)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
The chart shows the number of research articles in the prominent journal Physics Review that were written by researchers in Europe during 1983 - 2003 ( represents 1983). Determine the logistic regression model for the data (Round all coefficients to two significant digits.) According to the model, how many Physics Review articles were published by U.S. researchers in 2001 ( )
A)5,300
B) 5,000
C) 6,100
D) 5,800
E) 5,700
A)5,300
B) 5,000
C) 6,100
D) 5,800
E) 5,700

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
The graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve). The logistic model is
where x is the household income in thousands of dollars. According to the model, what percentage of extremely wealthy households had computers
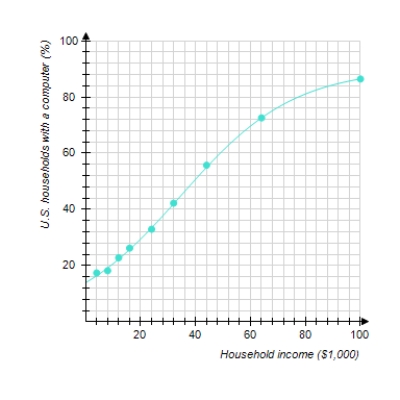
P = __________%
where x is the household income in thousands of dollars. According to the model, what percentage of extremely wealthy households had computers

P = __________%

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
In Russia the average consumer drank two servings of Coca-Cola in 1993. This amount appeared to be increasing exponentially with a doubling time of 2 years. Given a long-range market saturation estimate of 100 servings per year, find a logistic model for the consumption of Coca-Cola in Russia and use your model to predict when, to the nearest year, the average consumption will be 43 servings per year.
A)Sometime in 2005.
B) Sometime in 1993.
C) Sometime in 2003.
D) Sometime in 2004.
E) Sometime in 1994.
A)Sometime in 2005.
B) Sometime in 1993.
C) Sometime in 2003.
D) Sometime in 2004.
E) Sometime in 1994.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Find the logistic function f with the given properties. f has limiting value 12 and passes through (0, 3) and (1, 10).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
Find the logistic function f with the given properties. , f has limiting value 20, and for small values of x, f is approximately exponential and grows by 50% with every increase of 1 in x.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Last year's epidemic of Martian flu began with a single case in a total susceptible population of 10,000. The number of cases was increasing initially by 38% per day. Find a logistic model for the number of cases of Martian flu and use your model to predict the number of flu cases 2 weeks into the epidemic. Round your answer to the nearest integer.
A) cases
B) cases
C) cases
D) cases
E) cases
A) cases
B) cases
C) cases
D) cases
E) cases

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Find N, A, and b for the function given.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
The following graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve). The logistic model is
Where x is the household income in thousands of dollars. For low incomes, the logistic model is approximately exponential. Which exponential model best approximates P(x) for small x Round the coefficients to the nearest hundredth.
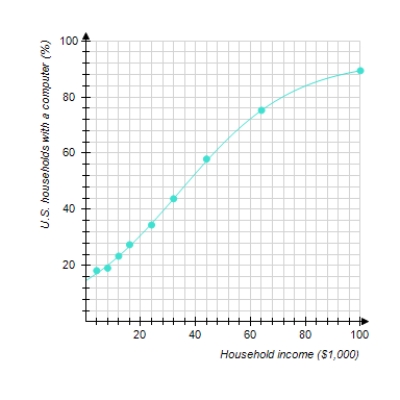
A)
B)
C)
D)
E)
Where x is the household income in thousands of dollars. For low incomes, the logistic model is approximately exponential. Which exponential model best approximates P(x) for small x Round the coefficients to the nearest hundredth.

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Choose the logistic function that best approximates the given curve. 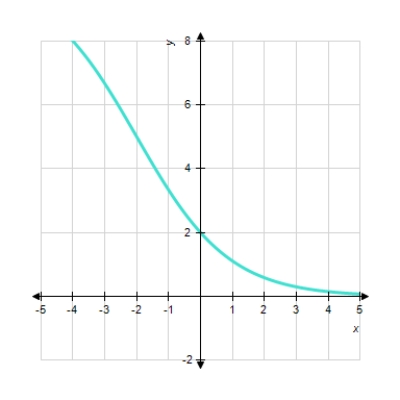
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Choose the logistic function that best approximates the curve. 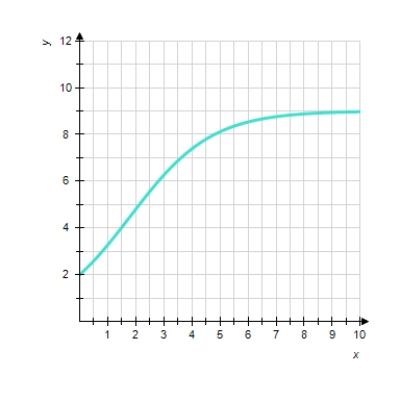
A)
B)
C)

A)
B)
C)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
Choose the logistic function that best approximates the curve. 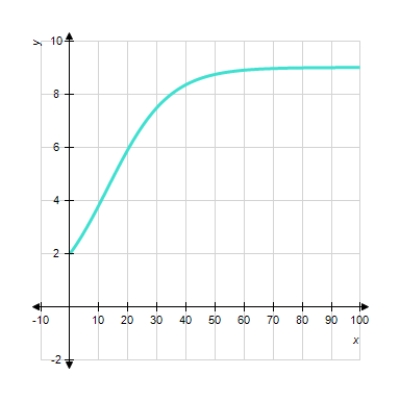
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Use technology to find a logistic regression curve approximating the given data. (Round b to three significant digits and A and N to two significant digits.)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
The graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve). The logistic model is
Where x is the household income in thousands of dollars. According to the model, what percentage of extremely wealthy households had computers
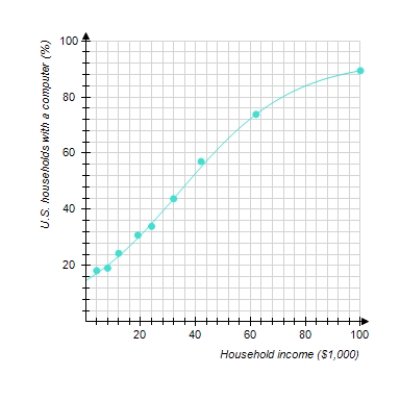
A) is close to .
B) is close to .
C) is close to .
D) is close to .
E) is close to .
Where x is the household income in thousands of dollars. According to the model, what percentage of extremely wealthy households had computers

A) is close to .
B) is close to .
C) is close to .
D) is close to .
E) is close to .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
Find the logistic function f with the given properties. , f has limiting value 500, and for small values of x, f is approximately exponential and doubles with every increase of 1 in x.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
Choose the logistic function that best approximates the given curve.
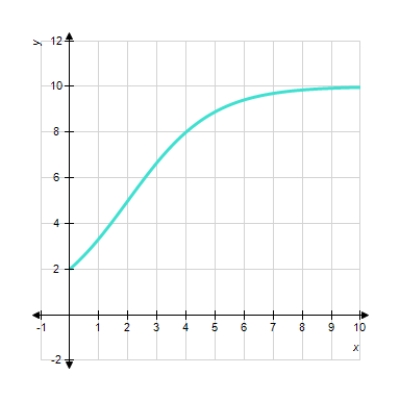
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Find the associated doubling time. 0.5t
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
Choose the logistic function that best approximates the curve. 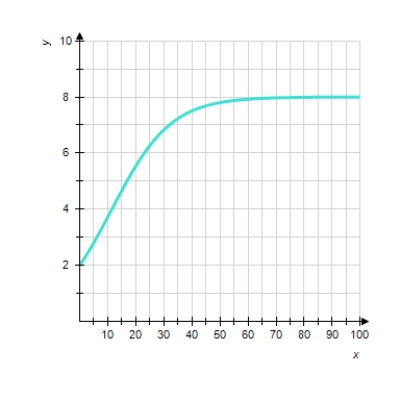
A)
B)
C)

A)
B)
C)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
Soon after taking an aspirin, a patient has absorbed 350 mg of the drug. If the amount of aspirin in the bloodstream decays exponentially, with half being removed every 2 hours, find the time it will take for the amount of aspirin in the bloodstream to decrease to 260 mg.
Select the answer rounded to three decimal places.
A)1.715 hours
B) 0.858 hours
C) 0.429 hours
D) 2.573 hours
E) 2.144 hours
Select the answer rounded to three decimal places.
A)1.715 hours
B) 0.858 hours
C) 0.429 hours
D) 2.573 hours
E) 2.144 hours

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
How long, to the nearest year, will it take an investment in U.S. to double its value if the interest is compounded every six months Please round the answer to the nearest year.
A)14 years
B) 16 years
C) 13 years
D) 8 years
E) 15 years
A)14 years
B) 16 years
C) 13 years
D) 8 years
E) 15 years

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
You are trying to determine the half-life of a new radioactive element you have isolated. You start with 2 grams, and 4 days later you determine that it has decayed down to 0.1 gram. What is the half-life Round your answer to three decimal places. ?
Select the answer rounded to three decimal places.
?
A)1.388 days
B) 1.851 days
C) 2.777 days
D) 0.463 days
E) 0.926 days
Select the answer rounded to three decimal places.
?
A)1.388 days
B) 1.851 days
C) 2.777 days
D) 0.463 days
E) 0.926 days

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Convert the exponential function to the form indicated. Round all coefficients to four significant digits.
;
A) ,
B) ,
C) ,
D) ,
E) ,
;
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
The chart shows the number of research articles in the prominent journal Physics Review that were written by researchers in Europe during 1983 - 2003 ( represents 1983). 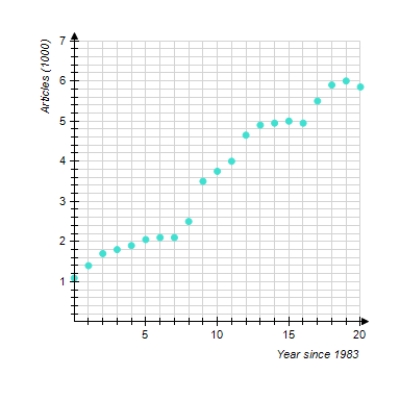
Which of the following logistic functions best models the data ( t is the number of years since 1983.) Try to determine the correct model without actually computing data points.
A)
B)
C)
D)
According to the model you selected, at what percentage was the number of articles growing around 1984
__________%

Which of the following logistic functions best models the data ( t is the number of years since 1983.) Try to determine the correct model without actually computing data points.
A)
B)
C)
D)
According to the model you selected, at what percentage was the number of articles growing around 1984
__________%

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
Find the associated exponential decay model. when ; Half-life = 9
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
Convert the exponential function to the form indicated. Round all coefficients to four significant digits.
;
A) ,
B) ,
C) ,
D) ,
E) ,
;
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
How long will it take an investment to triple if it is continuously compounded at 15% per year ?
Select the correct answer rounded to the nearest year.
A)15 years
B) 13 years
C) 8 years
D) 4 years
E) 7 years
Select the correct answer rounded to the nearest year.
A)15 years
B) 13 years
C) 8 years
D) 4 years
E) 7 years

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Use logarithms to solve the equation. (Round the answer to four decimal places.)
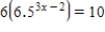
x = __________
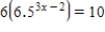
x = __________

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
Graph the function.
A)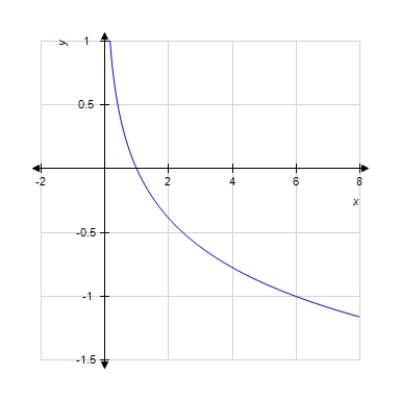
B)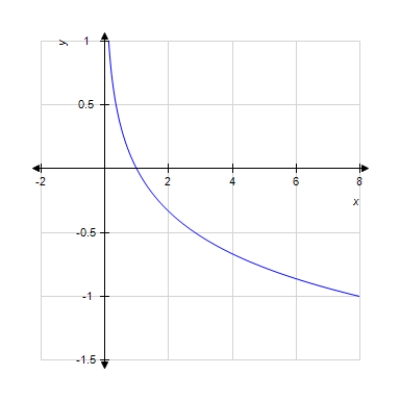
C)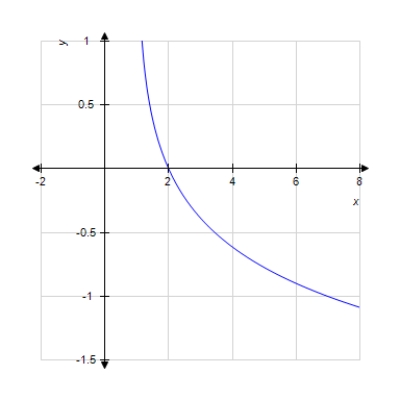
D)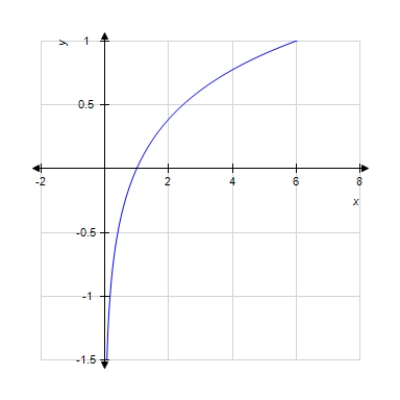
E)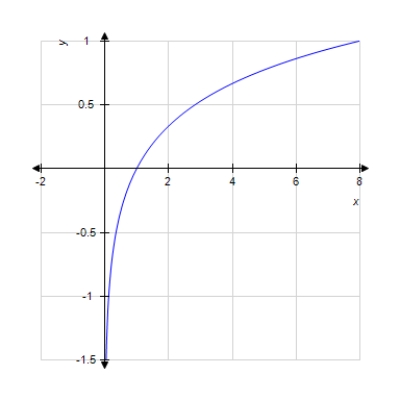
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
Use logarithms to solve the equation. Round your answer to four decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
Plutonium-239 is used as a fuel for some nuclear reactors and also as the fissionable material in atomic bombs. It has a half-life of 24,400 years. How long will it take 12 grams of plutonium-239 to decay to 2 grams ?
Round your answer to the nearest hundreds.
A)31,600 years
B) 15,800 years
C) 126,200 years
D) 63,100 years
E) 63,200 years
Round your answer to the nearest hundreds.
A)31,600 years
B) 15,800 years
C) 126,200 years
D) 63,100 years
E) 63,200 years

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Graph the function.
A)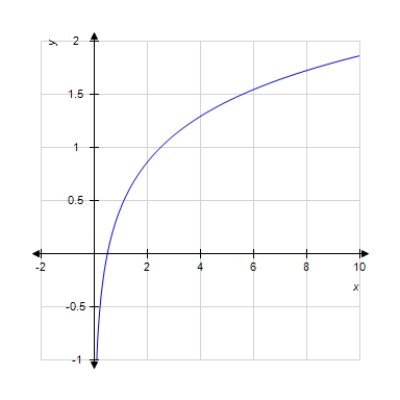
B)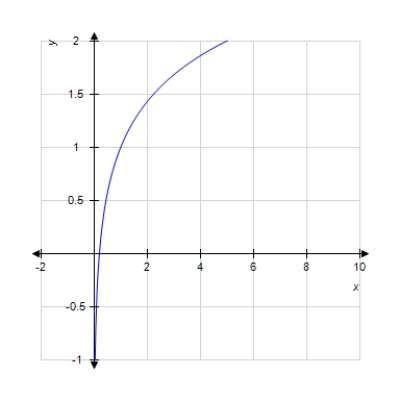
C)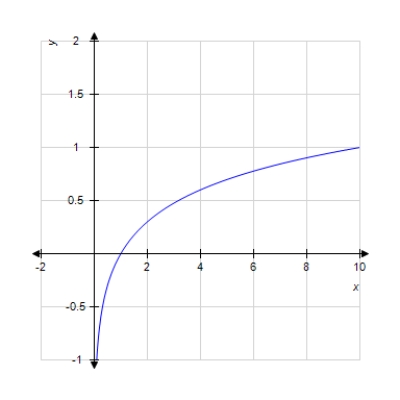
D)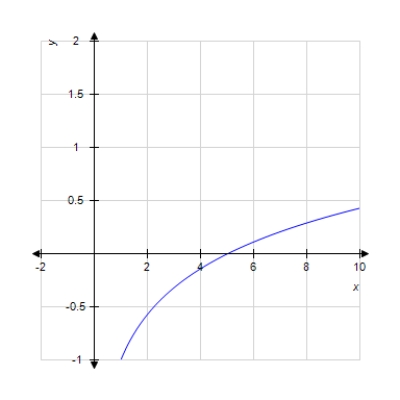
E)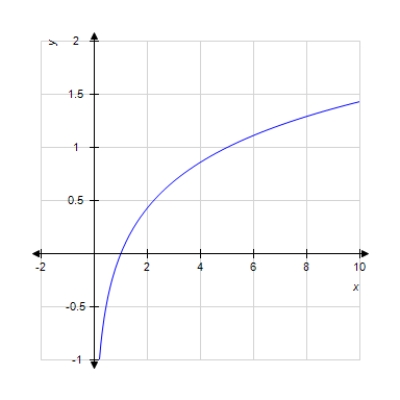
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
The chart shows the number of research articles in the prominent journal Physics Review that were written by researchers in Europe during 1983 - 2003 ( t=0 represents 1983)
a. What is the logistic regression model for the data (Round all coefficients to two significant digits.)
b. At what value does the model predict that the number of research articles will level off
__________ articles
b.c. According to the model, how many Physics Review articles were published by U.S. researchers in 1990 ( t=7)
a. What is the logistic regression model for the data (Round all coefficients to two significant digits.)
b. At what value does the model predict that the number of research articles will level off
__________ articles
b.c. According to the model, how many Physics Review articles were published by U.S. researchers in 1990 ( t=7)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
Use logarithms to solve the equation. Round your answer to four decimal places.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
The following graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve). The logistic model is
where x is the household income in thousands of dollars. For low incomes, the logistic model is approximately exponential. Which exponential model best approximates P(x) for small x Round the coefficients to the nearest hundredth.
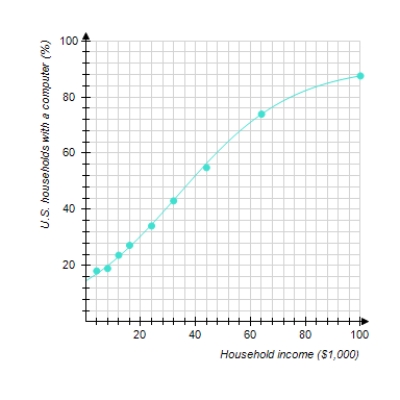
P(x) = ________ ·( ________)x
where x is the household income in thousands of dollars. For low incomes, the logistic model is approximately exponential. Which exponential model best approximates P(x) for small x Round the coefficients to the nearest hundredth.

P(x) = ________ ·( ________)x

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
The amount of carbon-14 remaining in a sample that weighs B is given by
where t is time in years. If tests on a fossilized skull reveal that 99.92% of the carbon-14 has decayed, how old is the skull
Select the correct answer rounded to the nearest integer.
A)58,929 years old
B) 2,629 years old
C) 1,985 years old
D) 0 years old
E) 23,234 years old
where t is time in years. If tests on a fossilized skull reveal that 99.92% of the carbon-14 has decayed, how old is the skull
Select the correct answer rounded to the nearest integer.
A)58,929 years old
B) 2,629 years old
C) 1,985 years old
D) 0 years old
E) 23,234 years old

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
The table lists interest rates on long-term investments (based on 10-year government bonds) in several countries in 2004-2005. Assuming that you invest $13,000 in Japan, how long (to the nearest year) must you wait before your investment is worth $19,000 if the interest is compounded annually Round your answer to the nearest year.
A)26 years
B) 19 years
C) 25 years
D) 22 years
E) 28 years
A)26 years
B) 19 years
C) 25 years
D) 22 years
E) 28 years

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
The table below is filled correctly.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Model the data using an exponential function . Select the correct answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Plutonium-239 is used as a fuel for some nuclear reactors and also as the fissionable material in atomic bombs. It has a half-life of 24,400 years. How long will it take 40 grams of plutonium-239 to decay to 3 grams
Round your answer to the nearest hundreds.
__________ years
Round your answer to the nearest hundreds.
__________ years

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
Model the data using an exponential function . Select the correct answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Find the associated exponential decay model.
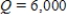 when
when 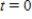 ; Half-life = 5
; Half-life = 5
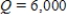 when
when 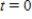 ; Half-life = 5
; Half-life = 5
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
How long, to the nearest year, will it take an investment in Canada to double its value if the interest is compounded every six months Please round the answer to the nearest year.
t = __________ year(s)
t = __________ year(s)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Rock Solid Bank & Trust is offering a CD that pays 5% compounded continuously. How much interest would a $1,000 deposit earn over 12 years (Round your answer to the nearest dollar.)
Select the correct answer.
A)$2,822
B) $822
C) $1,822
D) $1,820
E) $1,796
Select the correct answer.
A)$2,822
B) $822
C) $1,822
D) $1,820
E) $1,796

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Which of the following five functions will be largest for large values of x
Select the correct answer.
A)
B)
C)
D)
E)
Select the correct answer.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
Given the graph of the functions and . Identify which graph corresponds to . 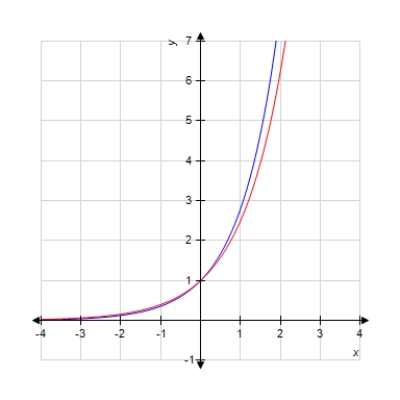
Select the correct answer.
A)Blue
B) Red

Select the correct answer.
A)Blue
B) Red

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
The U.S. population was 170 million in 1950 and 240 million in 1990. Assuming exponential population growth, what will the population be in the year 2020 Round your answer to the nearest million.
Select the correct answer.
A)250 million
B) 243 million
C) 486 million
D) 972 million
E) 311 million
Select the correct answer.
A)250 million
B) 243 million
C) 486 million
D) 972 million
E) 311 million

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
The table lists interest rates on long-term investments (based on 10-year government bonds) in several countries in 2004-2005. Assuming that you invest $12,000 in Japan, how long (to the nearest year) must you wait before your investment is worth $18,000 if the interest is compounded annually
__________ year(s)
__________ year(s)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Soon after taking an aspirin, a patient has absorbed 310 mg of the drug. If the amount of aspirin in the bloodstream decays exponentially with half being removed every 2 hours, find the amount of aspirin in the bloodstream after 9 hours.
Select the correct answer.
A)1,370
B) 137
C) 50
D) 13.7
E) 2.21
Select the correct answer.
A)1,370
B) 137
C) 50
D) 13.7
E) 2.21

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
Convert the exponential function to the form indicated. Round all coefficients to four significant digits.
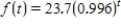 ;
; 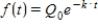


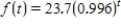 ;
; 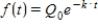



Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Graph the function.
Select the correct answer.
A)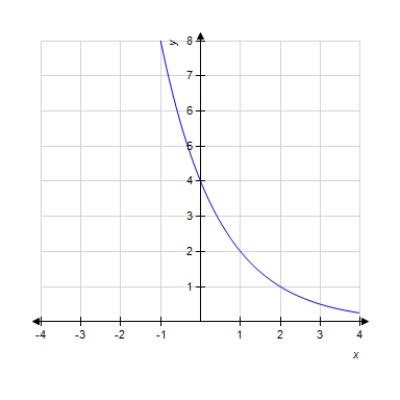
B)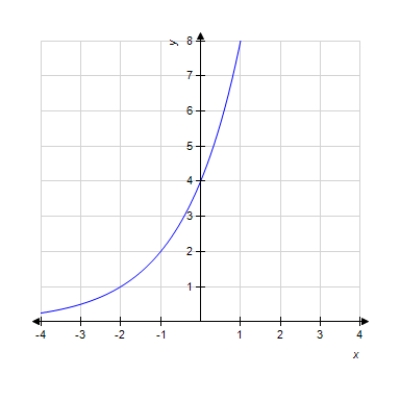
C)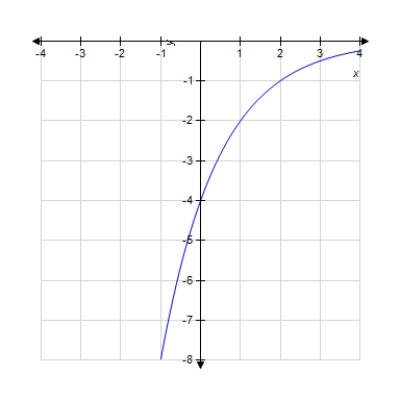
D)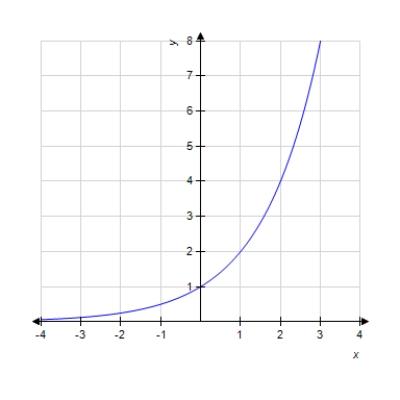
Select the correct answer.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
Model the data using an exponential function . Select the correct answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
How long, to the nearest year, will it take an investment to triple if it is continuously compounded at 15% per year
Round the answer to the nearest year.
__________ years
Round the answer to the nearest year.
__________ years

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
The table below is filled correctly.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
Find an equation for an exponential function that passes through the pair of points and .
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
Given the graph of the functions and . Determine the color of the graph that corresponds to . 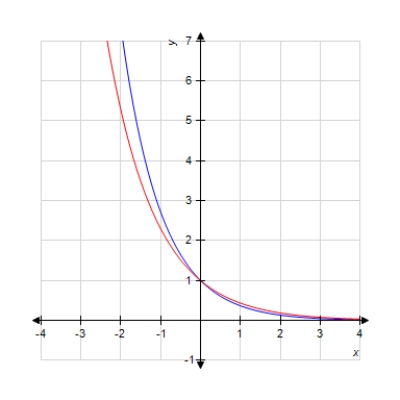
Select the correct answer.
A)Blue
B) Red

Select the correct answer.
A)Blue
B) Red

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
The table is filled correctly.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose the amount of carbon dioxide (in pounds per 15,000 miles) released by a typical sport utility vehicle (SUV) depends on its fuel efficiency according to the formula
Where x is a fuel efficiency of an SUV in miles per gallon. According to the model, what is the fuel efficiency of an SUV that has the least carbon dioxide pollution
A)14 miles per gallon
B) 19 miles per gallon
C) 18 miles per gallon
D) 32 miles per gallon
E) 29 miles per gallon
Where x is a fuel efficiency of an SUV in miles per gallon. According to the model, what is the fuel efficiency of an SUV that has the least carbon dioxide pollution
A)14 miles per gallon
B) 19 miles per gallon
C) 18 miles per gallon
D) 32 miles per gallon
E) 29 miles per gallon

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
The following chart shows the value of trade between two countries for the period 1994 - 2004 ( represents 1994). 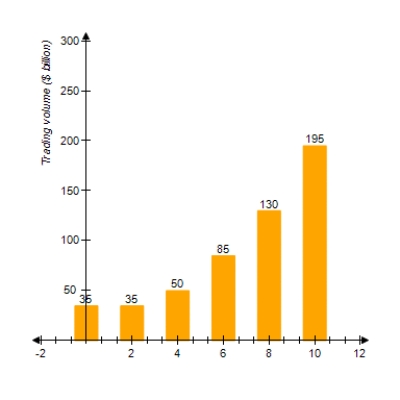
Which of the following models best approximates the data given (Try to answer this without actually computing values.)
A)
B)
C)
D)
E)

Which of the following models best approximates the data given (Try to answer this without actually computing values.)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Find the vertex of the graph of the quadratic function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
Model the data using an exponential function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
For the following demand equation, find the largest possible revenue.
A)3,200
B) 5,120,000
C) 7,680,000
D) 800
E) 2,560,000
A)3,200
B) 5,120,000
C) 7,680,000
D) 800
E) 2,560,000

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
The given table corresponds to the function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
The U.S. population was 170 million in 1970 and 250 million in 1995. Assuming exponential population growth, what will the population be in the year 2025
Round your answer to the nearest million.
__________ million
Round your answer to the nearest million.
__________ million

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
The fuel efficiency (in miles per gallon) of a sport utility vehicle (SUV) depends on its weight according to the formula
Where x is the weight of an SUV in pounds. According to the model, what is the weight of the least fuel-efficient SUV
A)3,000 pounds
B) 3,100 pounds
C) 2,000 pounds
D) 6,000 pounds
E) 491 pounds
Where x is the weight of an SUV in pounds. According to the model, what is the weight of the least fuel-efficient SUV
A)3,000 pounds
B) 3,100 pounds
C) 2,000 pounds
D) 6,000 pounds
E) 491 pounds

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
Find the y-intercept(s) of the graph of the quadratic function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
Which of the following five functions will be smallest for large values of x
Select the correct answer.
A)
B)
C)
D)
E)
Select the correct answer.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
The given table corresponds to the function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
The given table corresponds to the function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
Model the data using an exponential function 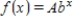 .
. 
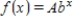 .
. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
Find the equation for the exponential function that passes through the pair of points 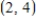 and
and 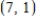 .
.
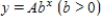
A = __________
b = __________
Round your answer to four decimal places.
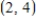 and
and 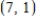 .
.
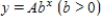
A = __________
b = __________
Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
The given table corresponds to the function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
The given table corresponds to the function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
Model the data using an exponential function 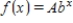 .
. 
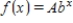 .
. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
The given table corresponds to the function .

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
For the following demand equation, find the largest possible revenue.
A)1,620,000
B) 450
C) 900
D) 810,000
E) 648,000
A)1,620,000
B) 450
C) 900
D) 810,000
E) 648,000

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
For the following demand equation, express the total revenue R as a function of the price p per item.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


