Deck 14: Further Integration Techniques and Applications of the Integral
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/118
Play
Full screen (f)
Deck 14: Further Integration Techniques and Applications of the Integral
1
For the differential equation, find the particular solution if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Your monthly sales of Tofu Ice Cream are falling at an instantaneous rate of 3% per month. If you currently sell per month, solve the differential equation that describes your change in sales to predict your monthly sales. Assume that the current sales are given for time .
NOTE: Enter your answer in the form , where f is some function of t.
A)
B)
C)
D)
E)
NOTE: Enter your answer in the form , where f is some function of t.
A)
B)
C)
D)
E)
3
You have just introduced a new computer to the market. You predict that you will eventually sell 99,000 computers and that your monthly rate of sales will be 17% of the difference between the saturation value and the total number you have sold up to that point. Solve the differential equation for your total sales s (as a function of the month). Hint: What are your total sales at the moment when you first introduce the computer
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
For the differential equation, find the particular solution if when .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
5
For the differential equation, find the particular solution if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
6
Find the general solution of the differential equation.
Solve for y as a function of x.
NOTE: Use the symbol C to enter the constant.
A)
B)
C)
D)
E)
Solve for y as a function of x.
NOTE: Use the symbol C to enter the constant.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
7
For the differential equation, find the particular solution when .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
8
Find the general solution of the differential equation. Solve for y as a function of x.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
9
Nancy's Chocolates estimates that the elasticity of demand for its dark chocolate truffles is
Where p is the price per pound. Nancy's sells 19 pounds of truffles per week when the price is $23 per pound. Find the formula expressing the demand q as a function of p. Recall that the elasticity of demand is given by .
NOTE: Round the value of the constant in your answer to four decimal places.
A)
B)
C)
D)
E)
Where p is the price per pound. Nancy's sells 19 pounds of truffles per week when the price is $23 per pound. Find the formula expressing the demand q as a function of p. Recall that the elasticity of demand is given by .
NOTE: Round the value of the constant in your answer to four decimal places.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
10
Your monthly profit p on sales of Avocado Ice Cream are rising at an instantaneous rate of 17% per month. If you currently make a profit of $14,500 per month, solve the differential equation that describes your change in profit to predict your monthly profits. Assume that the current sales are given for time .
A) .
B)
C)
D)
E)
A) .
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
11
For the given differential equation, find the particular solution when .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
12
Find the general solution of the differential equation.
Solve for y as a function of x.
A)
B)
C)
D)
E)
Solve for y as a function of x.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
13
Find the general solution of the differential equation.
Solve for y as a function of x.
A)
B)
C)
D)
E)
Solve for y as a function of x.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
14
Find the general solution of the differential equation.
Solve for y as a function of x.
A)
B)
C)
D)
E)
Solve for y as a function of x.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
15
For the given differential equation, find the particular solution if when .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
16
Find the general solution of the differential equation.
Solve for y as a function of x.
A)
B)
C)
D)
E)
Solve for y as a function of x.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
17
For the differential equation, find the particular solution if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
18
For the differential equation, find the particular solution if
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
19
Find the general solution of the differential equation.
Solve for y as a function of x.
A)
B)
C)
D)
E)
Solve for y as a function of x.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
20
For the given differential equation, find the particular solution if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
21
Decide whether the integral converges. If the integral converges, compute its value.
A)6
B) 9
C) 0
D) 18
E) diverges
A)6
B) 9
C) 0
D) 18
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
22
The Laplace transform F(x) of a function f (t ) is given by the formula.
Find if .
A)
B)
C)
D)
E)
Find if .
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
23
Decide whether the integral converges. If the integral converges, compute its value.
A)
B)
C)
D)
E) diverges
A)
B)
C)
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
24
The Laplace transform F(x) of a function f(t) is given by the formula.
Find F(x) if (n constant).
A)
B)
C)
D)
E)
Find F(x) if (n constant).
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
25
Decide whether the integral converges. If the integral converges, compute its value.
A)
B)
C)
D)
E) diverges
A)
B)
C)
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
26
Decide whether the integral converges. If the integral converges, compute its value.
A)converges to
B) converges to
C) converges to 8
D) converges to 0
E) diverges
A)converges to
B) converges to
C) converges to 8
D) converges to 0
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
27
Decide whether the integral converges. If the integral converges, compute its value.
A)
B)
C) 0
D)
E) diverges
A)
B)
C) 0
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
28
Decide whether the integral converges. If the integral converges, compute its value.
A)2
B) 1
C)
D) -2
E) diverges
A)2
B) 1
C)
D) -2
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
29
Decide whether the integral converges. If the integral converges, compute its value.
A)converges to 0
B) converges to 7
C) converges to 1
D) diverges
E) converges to 4
A)converges to 0
B) converges to 7
C) converges to 1
D) diverges
E) converges to 4

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
30
If the integral converges, compute its value.
A)
B)
C)
D)
E) diverges
A)
B)
C)
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
31
Decide whether the integral converges. If the integral converges, compute its value.
A)
B)
C)
D)
E) diverges
A)
B)
C)
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
32
Decide whether the integral converges. If the integral converges, compute its value.
A)
B)
C)
D)
E) diverges
A)
B)
C)
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
33
Decide whether the integral converges. If the integral converges, compute its value.
A)
B) 0
C)
D)
E) diverges
A)
B) 0
C)
D)
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
34
Decide whether the integral converges. If the integral converges, compute its value.
A)
B)
C)
D) 0
E) diverges
A)
B)
C)
D) 0
E) diverges

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
35
Decide whether the integral converges. If the integral converges, compute its value.
If the integral diverges, enter your answer as diverges .
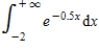
If the integral diverges, enter your answer as diverges .
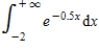

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
36
The weekly demand for your company's Lo-Cal Mousse is modeled by the equation where t is time from now in weeks and q(t) is the number of gallons sold per week. Evaluate the integral .
A)0.254 gallons
B) 5.639 gallons
C) 2.285 gallons
D) 1.142 gallons
E) 2.819 gallons
A)0.254 gallons
B) 5.639 gallons
C) 2.285 gallons
D) 1.142 gallons
E) 2.819 gallons

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the producers' surplus at the unit price for the following supply equation.
A)$80.00
B) $81.00
C) $86.00
D) $89.00
E) $83.00
A)$80.00
B) $81.00
C) $86.00
D) $89.00
E) $83.00

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
38
Calculate the producers' surplus at the unit price for the following supply equation.
A)$18.00
B) $11.00
C) $20.00
D) $12.00
E) $15.00
A)$18.00
B) $11.00
C) $20.00
D) $12.00
E) $15.00

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
39
Sales of the text "Calculus and You" have been declining continuously at an annual rate of 8%. Assuming that "Calculus and You" currently sell 800 copies per year and that sales will continue this pattern of decline, calculate total future sales of the text. Use the formula for continuously compounded interest with a negative rate.
A)100,000 copies
B) 80,000 copies
C) 10,000 copies
D) 250,000 copies
E) 500,000 copies
A)100,000 copies
B) 80,000 copies
C) 10,000 copies
D) 250,000 copies
E) 500,000 copies

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
40
The normal distribution curve, which models the distributions of data in a wide range of applications, is given by the function , and and are constants called the standard deviation and the mean, respectively. With and , approximate .
A)3
B) -5
C) 5
D) -1
E) 1
A)3
B) -5
C) 5
D) -1
E) 1

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
41
The annual revenue earned by Target for fiscal years 1998 through 2006 can be approximated by billion dollars per year where t is time in years ( represents the beginning of fiscal year 2000). Suppose that, from fiscal year 1998 on, Target invested its revenue in an investment that depreciated continuously at a rate of 5% per year. What, to the nearest $10 billion, would the total value of Target's revenue have been by the end of fiscal year 2004
A)Total revenue 40 billion dollars
B) Total revenue 220 billion dollars
C) Total revenue 2,200 billion dollars
D) Total revenue 110 billion dollars
E) Total revenue 20 billion dollars
A)Total revenue 40 billion dollars
B) Total revenue 220 billion dollars
C) Total revenue 2,200 billion dollars
D) Total revenue 110 billion dollars
E) Total revenue 20 billion dollars

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
42
The Megabucks Corporation is issuing a 20-year bond paying 7% interest. An investor wishes to buy the rights to receive the interest on $30,000 worth of these bonds and seeks a 12% rate of return. If the investor payments are made continuously, what will the investor pay Round your answer to the nearest cent. Round your answer to the nearest cent.
A)$159.12
B) $17,500.00
C) $210,405.59
D) $1,909.49
E) $15,912.44
A)$159.12
B) $17,500.00
C) $210,405.59
D) $1,909.49
E) $15,912.44

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
43
The annual net sales (revenue) earned by Nintendo Co., Ltd., in the fiscal years ending March 31, 1995 to March 31, 2003, can be approximated by billion yen per year where t is time in years ( represents March 31, 2000). Suppose that, from April 1994 on, Nintendo invested its revenue in an investment yielding 4% compounded continuously. What, to the nearest 100 billion, would the total value of Nintendo's revenue have been by the end of March 2003
A)Total revenue 500 billion yen
B) Total revenue 2,600 billion yen
C) Total revenue 1,000 billion yen
D) Total revenue 5,100 billion yen
E) Total revenue 51,200 billion yen
A)Total revenue 500 billion yen
B) Total revenue 2,600 billion yen
C) Total revenue 1,000 billion yen
D) Total revenue 5,100 billion yen
E) Total revenue 51,200 billion yen

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
44
Find the total value of the given income stream and also find its future value (at the end of the given interval) using the given interest rate. , , at 6%
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
45
Find the total value of the given income stream and also find its present value (at the beginning of the given interval) using the given interest rate. , , at 6%
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
46
The annual revenue earned by Wal-Mart in the fiscal years ending January 31, 1994 to January 31, 2002 can be approximated by billion dollars per year where t is time in years ( represents January 31, 2000). Suppose that, from January 1999 on, Wal-Mart invested its revenue in an investment that depreciated continuously at a rate of 4% per year. What, to the nearest $10 billion, would the total value of Wal-Mart's revenues have been by the end of January 2002
A)Total revenue 460 billion dollars
B) Total revenue 4,600 billion dollars
C) Total revenue 50 billion dollars
D) Total revenue 230 billion dollars
E) Total revenue 90 billion dollars
A)Total revenue 460 billion dollars
B) Total revenue 4,600 billion dollars
C) Total revenue 50 billion dollars
D) Total revenue 230 billion dollars
E) Total revenue 90 billion dollars

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
47
The U. S. Treasury issued a 20-year bond on November 16, 1998, paying 6.07% interest. Thus, if you bought $100,000 worth of these bonds, you would receive $6,070 per year in interest for 20 years. At investor wishes to buy the rights to receive the interest on $100,000 worth of these bonds. The amount the investor is willing to pay is the present value of the interest payments, assuming a 6% rate of return. If we assume (incorrectly, but approximately) that the interest payments are made continuously, what will the investor pay Round your answer to the nearest cent.
A)$70,695.85
B) $437,051.83
C) $335,885.16
D) $69,880.58
E) $706.96
A)$70,695.85
B) $437,051.83
C) $335,885.16
D) $69,880.58
E) $706.96

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
48
The annual net sales (revenue) earned by the Finnish cell phone company Nokia from January 1999 to January 2003 can be approximated by billion euros per year where t is time in years ( represents January 2000). Estimate, to the nearest billion, Nokia's total revenue from January 1999 through December 2002.
A)Total revenue 116 billion euros
B) Total revenue 120 billion euros
C) Total revenue 91 billion euros
D) Total revenue 4 billion euros
E) Total revenue 20 billion euros
A)Total revenue 116 billion euros
B) Total revenue 120 billion euros
C) Total revenue 91 billion euros
D) Total revenue 4 billion euros
E) Total revenue 20 billion euros

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
49
You are saving for your retirement by investing $1000 per month in an annuity with a guaranteed interest rate of 6% per year. With a continuous stream of investment and continuous compounding, how much will you have accumulated in the annuity by the time you retire in 15 years Round your answer to the nearest cent.
A)$180,000.00
B) $1,459.60
C) $691,920.62
D) $281,313.93
E) $291,920.62
A)$180,000.00
B) $1,459.60
C) $691,920.62
D) $281,313.93
E) $291,920.62

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
50
Find the total value of the given income stream and also find its present value (at the beginning of the given interval) using the given interest rate. , , at 9%
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
51
Find the total value of the given income stream and also find its future value (at the end of the given interval) using the given interest rate.
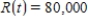 ,
, 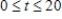 , at 11%
, at 11%
Please enter your answer in the form TV = , FV = . Round FV to the nearest cent.
TV = $__________ FV = $__________
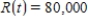 ,
, 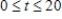 , at 11%
, at 11%
Please enter your answer in the form TV = , FV = . Round FV to the nearest cent.
TV = $__________ FV = $__________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
52
When your first child is born, you begin to save for college by depositing $600 per month in an account paying 6% interest per year. With a continuous stream of investment and continuous compounding, how much will you have accumulated in the account by the time your child enters college 18 years later Round your answer to the nearest cent.
A)$233,361.55
B) $353,361.55
C) $1,166.81
D) $473,361.55
E) $79,248.54
A)$233,361.55
B) $353,361.55
C) $1,166.81
D) $473,361.55
E) $79,248.54

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
53
Calculate the producers' surplus at the unit price 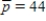 for the following supply equation.
for the following supply equation.
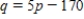
$ __________
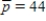 for the following supply equation.
for the following supply equation.
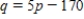
$ __________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
54
Find the total value or the given income stream and also find its future value (at the end of the given interval) using the given interest rate. , , at 7%
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
55
A fast-food outlet finds that the demand equation for its new side dish, "Sweetdough Tidbit", is given by where p is the price (in cents) per serving and q is the number of servings that can be sold per hour at this price. At the same time, the franchise is prepared to sell servings per hour at a price of p cents. Find the consumers' surplus at the equilibrium price level.
A)$6.06
B) $6.04
C) $6.00
D) $6.10
E) $6.02
A)$6.06
B) $6.04
C) $6.00
D) $6.10
E) $6.02

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
56
The annual net sales (revenue) earned by the Finnish cell phone company Nokia from January 1999 to January 2004 can be approximated by billion euros per year where t is time in years ( represents January 2000). Suppose that, from January 1999 on, Nokia invested its revenue in an investment yielding 7% compounded continuously. What, to the nearest €10 billion, would the total value of Nokia's revenues have been at the end of 2003
A)Total revenue 150 billion euros
B) Total revenue 180 billion euros
C) Total revenue 160 billion euros
D) Total revenue 170 billion euros
E) Total revenue 190 billion euros
A)Total revenue 150 billion euros
B) Total revenue 180 billion euros
C) Total revenue 160 billion euros
D) Total revenue 170 billion euros
E) Total revenue 190 billion euros

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
57
Find the total value of the given income stream and also find its future value (at the end of the given interval) using the given interest rate. , , at 8%
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
58
When your first child is born, you begin to save for college by depositing $500 per month in an account paying 12% interest per year. You increase the amount you save by 2% per year. With continuous investment and compounding, how much will you have accumulated in the account by the time your child enters college 18 years later Round your answer to the nearest cent.
A)$434,268.49
B) $4,342.68
C) $4,247,097.21
D) $5,052.23
E) $50,082.07
A)$434,268.49
B) $4,342.68
C) $4,247,097.21
D) $5,052.23
E) $50,082.07

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
59
You are saving for your retirement by investing $500 per month in an annuity with a guaranteed interest rate of 6% per year. You increase the amount you invest at the rate of 3% per year. With continuous investment and compounding, how much will you have accumulated in the annuity by the time you retire in 35 years Round your answer to the nearest cent.
A)$1,061,703.76
B) $130,012.45
C) $95,283.13
D) $10,617.04
E) $12,160,006.57
A)$1,061,703.76
B) $130,012.45
C) $95,283.13
D) $10,617.04
E) $12,160,006.57

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
60
Find the total value of the given income stream and also find its present value (at the beginning of the given interval) using the given interest rate. , , at 11%
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
61
Calculate the 11-unit moving average of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
62
Calculate the 5-unit moving average of the given function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
63
Find the total value of the given income stream and also find its present value (at the beginning of the given interval) using the given interest rate.
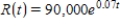 ,
, 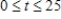 , at 10%
, at 10%
Please enter your answer in the form TV = , PV = . Give the answer to the nearest cent if necessary.
TV = $__________ PV = $__________
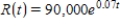 ,
, 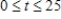 , at 10%
, at 10%
Please enter your answer in the form TV = , PV = . Give the answer to the nearest cent if necessary.
TV = $__________ PV = $__________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
64
Some values of a function and its 3-unit moving average are given. Supply the missing information:
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
65
If you invest $20,000 at 7% interest compounded continuously, what is the average amount in your account over 1 year
Please round your answer to the nearest cent.
A)$20,700.00
B) $5,350.00
C) $10,700.00
D) $21,400.00
E) $20,716.62
Please round your answer to the nearest cent.
A)$20,700.00
B) $5,350.00
C) $10,700.00
D) $21,400.00
E) $20,716.62

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
66
Find the average of the function over .
A)Average = 5
B) Average = 6
C) Average = 12
D) Average = 10
E) Average = 7
A)Average = 5
B) Average = 6
C) Average = 12
D) Average = 10
E) Average = 7

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
67
Find the formula for the a-unit moving average of a general exponential function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
68
Find the total value of the given income stream and also find its present value (at the beginning of the given interval) using the given interest rate.
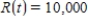 ,
, 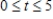 , at 5%
, at 5%
Please enter your answer in the form TV = , PV = . Give the answer to the nearest cent if necessary.
TV = $__________ PV = $__________
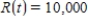 ,
, 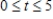 , at 5%
, at 5%
Please enter your answer in the form TV = , PV = . Give the answer to the nearest cent if necessary.
TV = $__________ PV = $__________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
69
Find the average of the function over .
A)Average = 32
B) Average = 64
C) Average = 256
D) Average = 1,024
E) Average = 1,028
A)Average = 32
B) Average = 64
C) Average = 256
D) Average = 1,024
E) Average = 1,028

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
70
Your monthly salary has been increasing steadily for the past year, and your average monthly salary over the past year was x dollars. Would you have earned more money if you had been paid ?x dollars per month ?
A)No. You would have earned exactly the same amount of money.
B) No. You would have earned less money.
C) Yes. You would have earned more money.
D) More information is needed to answer the question.
A)No. You would have earned exactly the same amount of money.
B) No. You would have earned less money.
C) Yes. You would have earned more money.
D) More information is needed to answer the question.

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
71
If you invest $12,000 at 9% interest compounded continuously, what is the average amount in your account over one year Round your answer to the nearest cent.
A)$12,556.57
B) $12,460.54
C) $12,844.66
D) $12,652.60
E) $12,748.63
A)$12,556.57
B) $12,460.54
C) $12,844.66
D) $12,652.60
E) $12,748.63

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
72
Find the total value of the given income stream and also find its present value (at the beginning of the given interval) using the given interest rate.
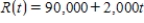 ,
, 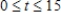 , at 11%
, at 11%
Please enter your answer in the form TV = , PV = . Give the answer to the nearest cent if necessary.
TV = $__________ PV = $__________
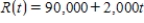 ,
, 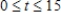 , at 11%
, at 11%
Please enter your answer in the form TV = , PV = . Give the answer to the nearest cent if necessary.
TV = $__________ PV = $__________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
73
Find the total value or the given income stream and also find its future value (at the end of the given interval) using the given interest rate.
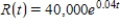 ,
, 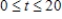 , at 7%
, at 7%
Please enter your answer in the form TV = , FV = . Give the answers to the nearest cent.
TV = $__________ FV = $__________
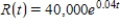 ,
, 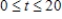 , at 7%
, at 7%
Please enter your answer in the form TV = , FV = . Give the answers to the nearest cent.
TV = $__________ FV = $__________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
74
Complete the table with the values of the 3-unit moving average of the given function:
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
75
Calculate the 5-unit moving average of the given function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
76
Calculate the 7-unit moving average of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
77
Find the average of the function over .
A)Average =
B) Average =
C) Average =
D) Average =
E) Average =
A)Average =
B) Average =
C) Average =
D) Average =
E) Average =

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
78
The rate of U.S. per capita sales of bottled water for the period 1993-2003 could be approximated by where t is the time in years since 1990.
Compute the average annual sales of bottled water over the period 1996-2003, to the nearest gallon per year.
A)16 gallons per year
B) 15 gallons per year
C) 17 gallons per year
D) 18 gallons per year
E) 19 gallons per year
Compute the average annual sales of bottled water over the period 1996-2003, to the nearest gallon per year.
A)16 gallons per year
B) 15 gallons per year
C) 17 gallons per year
D) 18 gallons per year
E) 19 gallons per year

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
79
Find the total value of the given income stream and also find its future value (at the end of the given interval) using the given interest rate.
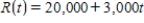 ,
, 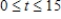 , at 10%
, at 10%
Please enter your answer in the form TV = , FV = . Round FV to the nearest cent.
TV = $__________ FV = $__________
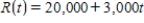 ,
, 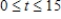 , at 10%
, at 10%
Please enter your answer in the form TV = , FV = . Round FV to the nearest cent.
TV = $__________ FV = $__________

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck
80
Find the formula for the c-unit moving average of a general linear function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 118 flashcards in this deck.
Unlock Deck
k this deck


