Deck 5: Matrix Algebra and Applications
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/174
Play
Full screen (f)
Deck 5: Matrix Algebra and Applications
1
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars): How much additional production by the Sector 1 is necessary to accommodate a $1,000 increase in the demand for the products of Sector 4 Please round your answer to two decimal places.
A)$12.78 million
B) $12.38 million
C) $12.58 million
D) $12.28 million
E) $12.08 million
A)$12.78 million
B) $12.38 million
C) $12.58 million
D) $12.28 million
E) $12.08 million
$12.38 million
2
Given the technology matrix A, and an external demand vector D, find the production vector X.
,
A)
B)
C)
D)
E)
,
A)
B)
C)
D)
E)
3
Each unit of television news requires 1.1 units of television news and 0.1 units of radio news. Each unit of radio news requires 0.3 units of television news and no radio news. With sector 1 as television news and sector 2 as radio news, set up the technology matrix A .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Two sectors of any country economy are (1) audio, video, and communication equipment and (2) electronic components and accessories. In 1998, the input-output table involving these two sectors was as follows (all figures are in millions of dollars):
Determine the production levels necessary in these two sectors to meet an external demand for $60,000 million of communication equipment and $90,000 million of electronic components. Round answers to two significant digits.
A)Equipment Sector production approximately $64,195.33 million, Components Sector production approximately $154,804.67 million.
B) Equipment Sector production approximately $67,195.33 million, Components Sector production approximately $154,804.67 million.
C) Equipment Sector production approximately $64,195.33 million, Components Sector production approximately $144,804.67 million.
D) Equipment Sector production approximately $67,195.33 million, Components Sector production approximately $144,804.67 million.
E) Equipment Sector production approximately $144,804.67 million, Components Sector production approximately $64,195.33 million.
Determine the production levels necessary in these two sectors to meet an external demand for $60,000 million of communication equipment and $90,000 million of electronic components. Round answers to two significant digits.
A)Equipment Sector production approximately $64,195.33 million, Components Sector production approximately $154,804.67 million.
B) Equipment Sector production approximately $67,195.33 million, Components Sector production approximately $154,804.67 million.
C) Equipment Sector production approximately $64,195.33 million, Components Sector production approximately $144,804.67 million.
D) Equipment Sector production approximately $67,195.33 million, Components Sector production approximately $144,804.67 million.
E) Equipment Sector production approximately $144,804.67 million, Components Sector production approximately $64,195.33 million.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
5
Two sectors of some economy are Sector 1 and Sector 2. The input-output table involving these two sectors results in the following value for
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 2
A)$0.00536
B) $0.54825
C) $1.07515
D) $1.0965
E) $0.04361
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 2
A)$0.00536
B) $0.54825
C) $1.07515
D) $1.0965
E) $0.04361

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
6
Production of 1 unit of cologne requires 0.9 units of perfume and 0.4 units of cologne. Into 1 unit of perfume goes 0.2 unit of perfume and 0.5 units of cologne. With sector 1 as cologne and sector 2 as perfume, set up the technology matrix A.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
7
Two sectors of any country economy are (1) lumber and wood products and (2) paper and allied products. In 1998 the input-output table involving these two sectors was as follows (all figures are in millions of dollars). If external demand for lumber and wood products rises by $14,000 million and external demand for paper and allied products rises by $22,000 million, what increase in output of these two sectors is necessary Round answers to two significant digits.
A)increase in output of lumber and wood products is $22,137.71 million and increase in output of paper and allied products is $25,652.56 million
B) increase in output of lumber and wood products is $24,137.71 million and increase in output of paper and allied products is $28,652.56 million
C) increase in output of lumber and wood products is $21,137.71 million and increase in output of paper and allied products is $25,652.56 million
D) increase in output of lumber and wood products is $19,137.71 million and increase in output of paper and allied products is $23,652.56 million
E) increase in output of lumber and wood products is $22,137.71 million and increase in output of paper and allied products is $23,652.56 million
A)increase in output of lumber and wood products is $22,137.71 million and increase in output of paper and allied products is $25,652.56 million
B) increase in output of lumber and wood products is $24,137.71 million and increase in output of paper and allied products is $28,652.56 million
C) increase in output of lumber and wood products is $21,137.71 million and increase in output of paper and allied products is $25,652.56 million
D) increase in output of lumber and wood products is $19,137.71 million and increase in output of paper and allied products is $23,652.56 million
E) increase in output of lumber and wood products is $22,137.71 million and increase in output of paper and allied products is $23,652.56 million

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
8
Let A be the technology matrix, where Sector 1 is computer chips, and Sector 2 is silicon.
How many units of computer chips are needed to produce one unit of silicon
How many units of silicon are needed to produce one unit of silicon
How many units of silicon are needed to produce one unit of computer chips
A) computer chips silicon:
silicon silicon:
silicon computer chips:
B) computer chips silicon:
silicon silicon:
silicon computer chips:
C) computer chips silicon:
silicon silicon:
silicon computer chips:
D) computer chips silicon:
silicon silicon:
silicon computer chips:
E) computer chips silicon:
silicon silicon:
silicon computer chips:
How many units of computer chips are needed to produce one unit of silicon
How many units of silicon are needed to produce one unit of silicon
How many units of silicon are needed to produce one unit of computer chips
A) computer chips silicon:
silicon silicon:
silicon computer chips:
B) computer chips silicon:
silicon silicon:
silicon computer chips:
C) computer chips silicon:
silicon silicon:
silicon computer chips:
D) computer chips silicon:
silicon silicon:
silicon computer chips:
E) computer chips silicon:
silicon silicon:
silicon computer chips:

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
9
Let and assume that the external demand for the products in each of the sectors increases by 1 unit. By how many units should each sector increase production
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
10
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars) How much additional production by the Sector 3 is necessary to accommodate a $100 increase in the demand for the products of Sector 1
A)$1.14
B) $0.72
C) $0.96
D) $0.42
E) $0.83
A)$1.14
B) $0.72
C) $0.96
D) $0.42
E) $0.83

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
11
Let and assume that the external demand for the products in Sector 1 increases by 1 unit. By how many units should each sector increase production
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
12
Let A be the technology matrix, where Sector 1 is paper, and Sector 2 is wood.
How many units of wood are needed to produce one unit of paper
How many units of paper are needed to produce one unit of paper
How many units of paper are needed to produce one unit of wood
A) Wood Paper:
Paper Paper:
Paper Wood:
B) Wood Paper:
Paper Paper:
Paper Wood:
C) Wood Paper:
Paper Paper:
Paper Wood:
D) Wood Paper:
Paper Paper:
Paper Wood:
E) Wood Paper:
Paper Paper:
Paper Wood:
How many units of wood are needed to produce one unit of paper
How many units of paper are needed to produce one unit of paper
How many units of paper are needed to produce one unit of wood
A) Wood Paper:
Paper Paper:
Paper Wood:
B) Wood Paper:
Paper Paper:
Paper Wood:
C) Wood Paper:
Paper Paper:
Paper Wood:
D) Wood Paper:
Paper Paper:
Paper Wood:
E) Wood Paper:
Paper Paper:
Paper Wood:

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
13
Two student groups at Enormous State University, the Choral Society and the Football Club, maintain files of term papers that they write and offer to students for research purposes. Some of these papers they use themselves in generating more papers. To avoid suspicion of plagiarism by faculty members (who seem to have astute memories), each paper is given to students or used by the clubs only once (no copies are kept). The number of papers that were used in the production of new papers last year is shown in the input-output table below. Given that 990 Choral Society papers and 1,485 Football Club papers will be used by students outside of these two clubs next year, how many new papers do the two clubs need to write
A)Choral Society 1,780, Football Club 2,480
B) Choral Society 1,730, Football Club 2,524
C) Choral Society 1,812, Football Club 2,466
D) Choral Society 1,770, Football Club 2,450
E) Choral Society 2,500, Football Club 1,830
A)Choral Society 1,780, Football Club 2,480
B) Choral Society 1,730, Football Club 2,524
C) Choral Society 1,812, Football Club 2,466
D) Choral Society 1,770, Football Club 2,450
E) Choral Society 2,500, Football Club 1,830

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
14
Given the technology matrix A, and an external demand vector D, find the production vector X. Round your answer to one decimal places. ,
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
15
Given the technology matrix A, and an external demand vector D, find the production vector X.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
16
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars) Determine how these four sectors would react to an increase in demand for Sector 1 production of $1,000 million.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
17
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars) Determine how these four sectors would react to an increase in demand for Sector 1 production of $1000 million.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
18
Two sectors of some economy are Sector 1 and Sector 2. The input-output table involving these two sectors results in the following value for
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 1
A)$1.1242
B) $0.9692
C) $0.002
D) $1.21
E) $0.155
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 1
A)$1.1242
B) $0.9692
C) $0.002
D) $1.21
E) $0.155

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
19
Given the technology matrix A, and an external demand vector D, find the production vector X.
,
A)
B)
C)
D)
E)
,
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
20
Obtain the technology matrix from the input-output table.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
21
Given the technology matrix A, and an external demand vector D, find the production vector X.
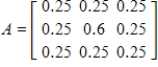 ,
, 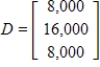
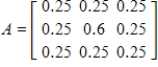 ,
, 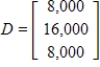

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
22
Let A be the technology matrix, where Sector 1 = wood, and Sector 2 = paper.
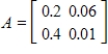
__________ units of paper are needed to produce one unit of wood.
__________ units of wood are needed to produce one unit of paper.
The production of each unit of paper requires the use of __________ units of paper.
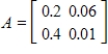
__________ units of paper are needed to produce one unit of wood.
__________ units of wood are needed to produce one unit of paper.
The production of each unit of paper requires the use of __________ units of paper.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
23
Given the technology matrix A, and an external demand vector B, find the production vector X.
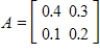 ,
, 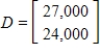
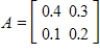 ,
, 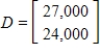

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
24
Let and assume that the external demand for the products in Sector 1 increases by 1 unit. By how many units should each sector increase production
?
Express the answer as a column matrix.
?
Express the answer as a column matrix.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
25
Each unit of television news requires 0.5 units of television news and 0.4 units of radio news. Each unit of radio news requires 0.7 units of television news and no radio news. With sector 1 as television news and sector 2 as radio news, set up the technology matrix A.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
26
Production of 1 unit of cologne requires 0.7 units of perfume and 0.3 units of cologne. Into 1 unit of perfume goes 0.2 unit of perfume and 0.4 units of cologne. With sector 1 as cologne and sector 2 as perfume, set up the technology matrix A.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
27
Given the technology matrix A, and an external demand vector D, find the production vector X.
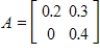 ,
, 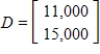
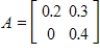 ,
, 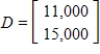

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
28
Two student groups at Enormous State University, the Choral Society and the Football Club, maintain files of term papers that they write and offer to students for research purposes. Some of these papers they use themselves in generating more papers. To avoid suspicion of plagiarism by faculty members (who seem to have astute memories), each paper is given to students or used by the clubs only once (no copies are kept). The number of papers that were used in the production of new papers last year is shown in the input-output table below.
Given that 110 Choral Society papers and 330 Football Club papers will be used by students outside of these two clubs next year, how many new papers do the two clubs need to write
Choral Society __________, Football Club __________
Given that 110 Choral Society papers and 330 Football Club papers will be used by students outside of these two clubs next year, how many new papers do the two clubs need to write
Choral Society __________, Football Club __________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
29
Two sectors of some economy are Sector 1 and Sector 2. The input-output table involving these two sectors results in the following value for
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 1 Round your answer to three decimal places.
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 1 Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
30
Given the technology matrix A, and an external demand vector D, find the production vector X.
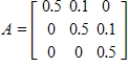 ,
, 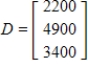
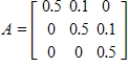 ,
, 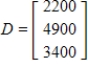

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
31
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars)
How much additional production by the Sector 3 is necessary to accommodate a $100 increase in the demand for the products of Sector 1 Round your answers to two decimal places.
$ __________
How much additional production by the Sector 3 is necessary to accommodate a $100 increase in the demand for the products of Sector 1 Round your answers to two decimal places.
$ __________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
32
Two sectors of some economy are Sector 1 and Sector 2. The input-output table involving these two sectors results in the following value for
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 2 Round your answer to four decimal places.
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 2 Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
33
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars)
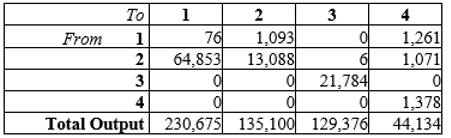


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
34
Obtain the technology matrix from the following input-output table. 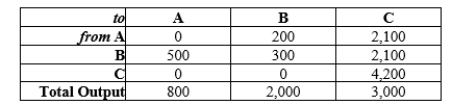


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
35
Let and assume that the external demand for the products in each of the sectors increases by 1 unit. By how many units should each sector increase production

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
36
Reduce the payoff matrix by dominance.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
37
Two sectors of any country economy are (1) audio, video, and communication equipment and (2) electronic components and accessories. In 1998, the input-output table involving these two sectors was as follows (all figures are in millions of dollars): 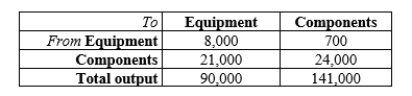
Determine the production levels necessary in these two sectors to meet an external demand for $80,000 million of communication equipment and $110,000 million of electronic components. Round answers to two significant digits.
Equipment Sector production approximately __________ million, Components Sector production approximately __________ million.

Determine the production levels necessary in these two sectors to meet an external demand for $80,000 million of communication equipment and $110,000 million of electronic components. Round answers to two significant digits.
Equipment Sector production approximately __________ million, Components Sector production approximately __________ million.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
38
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars):
How much additional production by the Sector 1 is necessary to accommodate a $1,000 increase in the demand for the products of Sector 4 Round your answer to two decimal places.
$ __________ million
How much additional production by the Sector 1 is necessary to accommodate a $1,000 increase in the demand for the products of Sector 4 Round your answer to two decimal places.
$ __________ million

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
39
Let be the technology matrix, be the production vector, and be the external demand vector.
There would be 0.4 units of sector 2 needed to produce one unit of sector 2.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
40
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars) 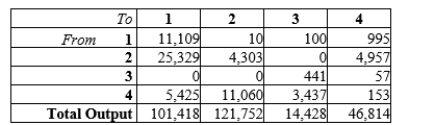
Determine how these four sectors would react to an increase in demand for Sector 1 production of $1,000 million. Round your answers to two decimal places.
Express the answer as a column matrix.

Determine how these four sectors would react to an increase in demand for Sector 1 production of $1,000 million. Round your answers to two decimal places.
Express the answer as a column matrix.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
41
Calculate the expected value of the game with the given payoff matrix using the mixed strategy supplied.
, ,
A)
B)
C)
D)
E)
, ,
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
42
City Community College (CCC) plans to host Midtown Military Academy (MMA) for a wrestling tournament. Each school has three wrestlers in the 190 lb. weight class: CCC has Pablo, Sal, and Edison, while MMA has Carlos, Marcus and Noto. Pablo can beat Carlos and Marcus, Marcus can beat Sal and Edison, Sal can beat Carlos, Noto can beat Edison, while the other combinations will result in an even match. Set up a payoff matrix, and use reduction by dominance to decide which wrestler each team should choose as their champion. Does one school have an advantage over the other ?
A)Pablo vs. Noto; evenly matched
B) Sal vs. Marcus; Marcus wins
C) Sal vs. Noto; evenly matched
D) Pablo vs. Carlos; Pablo wins
E) Sal vs. Carlos; evenly matched
A)Pablo vs. Noto; evenly matched
B) Sal vs. Marcus; Marcus wins
C) Sal vs. Noto; evenly matched
D) Pablo vs. Carlos; Pablo wins
E) Sal vs. Carlos; evenly matched

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
43
Reduce the payoff matrix by dominance.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
44
A farmer has a choice of growing wheat, barley, or rice. Her success will depend on the weather, which could be dry, average, or wet. Her payoff matrix is as follows. If the probability that the weather will be dry is 50%, the probability that it will be average is 10%, and the probability that it will be wet is 40%, what is the farmer's best choice of crop
A)Barley
B) Barley and Rice
C) Wheat
D) Wheat and Barley
E) Rice
A)Barley
B) Barley and Rice
C) Wheat
D) Wheat and Barley
E) Rice

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
45
For the given row strategy R, find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. ,
A)The strategy is ; the resulting expected value of the game is -1.2
B) The strategy is ; the resulting expected value of the game is -1.2
C) The strategy is ; the resulting expected value of the game is -0.7
D) The strategy is ; the resulting expected value of the game is -1.2
E) The strategy is ; the resulting expected value of the game is -0.2
A)The strategy is ; the resulting expected value of the game is -1.2
B) The strategy is ; the resulting expected value of the game is -1.2
C) The strategy is ; the resulting expected value of the game is -0.7
D) The strategy is ; the resulting expected value of the game is -1.2
E) The strategy is ; the resulting expected value of the game is -0.2

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
46
Reduce the payoff matrix by dominance.
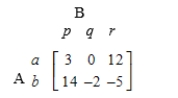
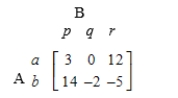

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
47
Your Abercrom B men's fashion outlet has a 60% chance of launching an expensive new line of used auto-mechanic dungarees (complete with grease stains) and a 40% chance of staying instead with its traditional torn military-style dungarees. Your rival across from you in the mall, Abercrom A, appears to be deciding between a line of torn gym shirts and a more daring line of "empty shirts" (that is, empty shirt boxes). Your corporate spies reveal that there is a 50% chance that Abercrom A will opt for the empty shirt option. The payoff matrix gives the number of customers your outlet can expect to gain from Abercrom A in each situation.
? ?
How many customers can you expect to lose Round the answer to the nearest whole.
?
__________ customers
? ?
How many customers can you expect to lose Round the answer to the nearest whole.
?
__________ customers

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
48
In the Second World War, during the struggle for New Guinea, intelligence reports revealed that the Japanese were planning to move a troop and supply convoy from the port of Rabaul at the Eastern tip of New Britain to Lae, which lies just west of New Britain on New Guinea. It could either travel via a northern route which was plagued by poor visibility, or by a southern route, where the visibility was clear. General Kenney, who was the commander of the Allied Air Forces in the area, had the choice of concentrating reconnaissance aircraft on one route or the other, and bombing the Japanese convoy once it was sighted. Suppose that General Kenney had a third alternative: Splitting his reconnaissance aircraft between the two routes Kenney's staff drafted the following outcomes for his choices, where the payoffs are estimated days of bombing time: What would you have recommended to General Kenney What would you have recommended to the Japanese Commander How much bombing time results if these recommendations are followed
A)General Kenney should use Split Reconnaissance and the Japanese Commander should use southern route; 3 days
B) General Kenney should use northern route and the Japanese Commander should use southern route; 2.5 days
C) Both commanders should use the northern route; 2 days
D) Both commanders should use the southern route; 1 days
E) General Kenney should use Split Reconnaissance and the Japanese Commander should use northern route; 0.5 days
A)General Kenney should use Split Reconnaissance and the Japanese Commander should use southern route; 3 days
B) General Kenney should use northern route and the Japanese Commander should use southern route; 2.5 days
C) Both commanders should use the northern route; 2 days
D) Both commanders should use the southern route; 1 days
E) General Kenney should use Split Reconnaissance and the Japanese Commander should use northern route; 0.5 days

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
49
Reduce the payoff matrix by dominance.
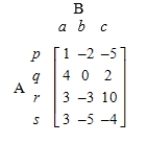
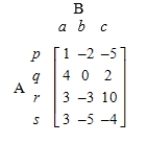

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
50
Your fast-food outlet, Burger Queen, has obtained a license to open branches in three closely situated South African cities: Brakpan, Nigel, and Springs. Your market surveys show that Brakpan and Nigel each provide a potential market of 2,500 burgers a day, while Springs provides a potential market of 1,000 burgers per day. Your company can only finance an outlet in one of those cities at the present time. Your main competitor, Burger Princess, has also obtained licenses for these cities, and is similarly planning to open only one outlet. If you both happen to locate at the same city, you will share the total business from all three cities equally, but if you locate in different cities, you will each get all the business in the cities in which you have located, plus half the business in the third city. The payoff is the number of burgers you will sell per day minus the number of burgers your competitor will sell per day. Set up the payoff matrix.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
51
Decide whether the game is strictly determined. If it is, give the players' optimal pure strategies and the value of the game.
A)A's optimal strategy is Q; B's optimal strategy is a; value: 0.5
B) A's optimal strategy is P; B's optimal strategy is a; value: 1
C) A's optimal strategy is P; B's optimal strategy is b; value: 1
D) A's optimal strategy is R; B's optimal strategy is c; value: 3
E) The game is not strictly determined
A)A's optimal strategy is Q; B's optimal strategy is a; value: 0.5
B) A's optimal strategy is P; B's optimal strategy is a; value: 1
C) A's optimal strategy is P; B's optimal strategy is b; value: 1
D) A's optimal strategy is R; B's optimal strategy is c; value: 3
E) The game is not strictly determined

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
52
You and your friend have come up with the following simple game to pass the time: at each round, you simultaneously call "heads" or "tails". If you have both called the same thing, your friend wins one point; if your calls differ, you win one point. Set up the payoff matrix.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
53
Decide whether the game is strictly determined. If it is, give the players' optimal pure strategies and the value of the game.
A)A's optimal strategy is a; B's optimal strategy is q; value: 1
B) A's optimal strategy is b; B's optimal strategy is q; value: 1
C) A's optimal strategy is b; B's optimal strategy is p; value: 1
D) A's optimal strategy is a; B's optimal strategy is p; value: 1.5
E) The game is not strictly determined
A)A's optimal strategy is a; B's optimal strategy is q; value: 1
B) A's optimal strategy is b; B's optimal strategy is q; value: 1
C) A's optimal strategy is b; B's optimal strategy is p; value: 1
D) A's optimal strategy is a; B's optimal strategy is p; value: 1.5
E) The game is not strictly determined

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
54
Your Abercrom B men's fashion outlet has a 40% chance of launching an expensive new line of used auto-mechanic dungarees (complete with grease stains) and a 60% chance of staying instead with its traditional torn military-style dungarees. Your rival across from you in the mall, Abercrom A, appears to be deciding between a line of torn gym shirts and a more daring line of "empty shirts" (that is, empty shirt boxes). Your corporate spies reveal that there is a 40% chance that Abercrom A will opt for the empty shirt option. The payoff matrix gives the number of customers your outlet can expect to gain from Abercrom A in each situation.
 What is the expected resulting effect on your customer base Round the answer to the nearest whole number.
What is the expected resulting effect on your customer base Round the answer to the nearest whole number.
A)You can expect to lose 3 customers.
B) You can expect to lose 4 customers.
C) You can expect to lose 5 customers.
D) You can expect to gain 3 customers.
E) You can expect to gain 4 customers.
 What is the expected resulting effect on your customer base Round the answer to the nearest whole number.
What is the expected resulting effect on your customer base Round the answer to the nearest whole number.A)You can expect to lose 3 customers.
B) You can expect to lose 4 customers.
C) You can expect to lose 5 customers.
D) You can expect to gain 3 customers.
E) You can expect to gain 4 customers.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
55
Find the optimal mixed row strategy, the optimal mixed column strategy, and the expected value of the game in the event that each player uses his or her optimal mixed strategy.
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
56
Decide whether the game is strictly determined. If it is, give the players' optimal pure strategies and the value of the game.
A)A's optimal strategy is b; B's optimal strategy is q; value: 0.5
B) A's optimal strategy is a; B's optimal strategy is p; value: 2
C) A's optimal strategy is a; B's optimal strategy is q; value: 1
D) A's optimal strategy is b; B's optimal strategy is p; value: 1
E) The game is not strictly determined.
A)A's optimal strategy is b; B's optimal strategy is q; value: 0.5
B) A's optimal strategy is a; B's optimal strategy is p; value: 2
C) A's optimal strategy is a; B's optimal strategy is q; value: 1
D) A's optimal strategy is b; B's optimal strategy is p; value: 1
E) The game is not strictly determined.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
57
A manufacturer of electrical machinery is located in a cramped, though low-rent, factory close to the center of a large city. The firm needs to expand, and it could do so in one of three ways: (1) remain where it is and install new equipment, (2) move to a suburban site in the same city, or (3) relocate in a different part of the country where labor is cheaper. Its decision will be influenced by the fact that one of the following will happen: (I) the government may introduce a program of equipment grants, (II) a new suburban highway may be built, or (III) the government may institute a policy of financial help to companies who move into regions of high unemployment. The value to the company of each combination is given in the following payoff matrix. If the manufacturer judges that there is a 60% probability that the government will go with option I, a 30% probability that they will go with option II, and a 10% probability that they will go with option III, what is the manufacturer's best option
A)Option 1
B) Option 3
C) Option 1 and Option 2
D) Option 2
E) Option 1 and Option 3
A)Option 1
B) Option 3
C) Option 1 and Option 2
D) Option 2
E) Option 1 and Option 3

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
58
For the given row strategy R, find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. Also determine the resulting expected value of the game. ,
A)The strategy is ; the resulting expected value of the game is -0.3
B) The strategy is ; the resulting expected value of the game is -1.3
C) The strategy is ; the resulting expected value of the game is -1.3
D) The strategy is ; the resulting expected value of the game is -1.3
E) The strategy is ; the resulting expected value of the game is -0.8
A)The strategy is ; the resulting expected value of the game is -0.3
B) The strategy is ; the resulting expected value of the game is -1.3
C) The strategy is ; the resulting expected value of the game is -1.3
D) The strategy is ; the resulting expected value of the game is -1.3
E) The strategy is ; the resulting expected value of the game is -0.8

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
59
Find the optimal mixed row strategy, the optimal mixed column strategy, and the expected value of the game in the event that each player uses his or her optimal mixed strategy.
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
60
You are deciding whether to invade England, Sweden or Norway, and your opponent is simultaneously deciding which of these three countries to defend. If you invade a country that your opponent is defending, you will be defeated (payoff: -1), but if you invade a country your opponent is not defending, you will be successful (payoff: +1). Set up the payoff matrix.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
61
Calculate the expected value of the game with the given payoff matrix using the mixed strategy supplied.
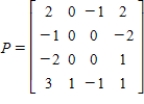 ,
, 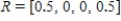 ,
, 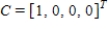
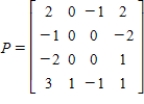 ,
, 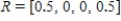 ,
, 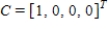

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
62
In the Second World War, during the struggle for New Guinea, intelligence reports revealed that the Japanese were planning to move a troop and supply convoy from the port of Rabaul at the Eastern tip of New Britain to Lae, which lies just west of New Britain on New Guinea. It could either travel via a northern route which was plagued by poor visibility, or by a southern route, where the visibility was clear. General Kenney, who was the commander of the Allied Air Forces in the area, had the choice of concentrating reconnaissance aircraft on one route or the other, and bombing the Japanese convoy once it was sighted. Suppose that General Kenney had a third alternative: Splitting his reconnaissance aircraft between the two routes Kenney's staff drafted the following outcomes for his choices, where the payoffs are estimated days of bombing time:
What would you have recommended to General Kenney
__________ (Northern Route or Split Reconnaissance or Southern Route)
What would you have recommended to the Japanese Commander
__________ (Northern Route or Southern Route)
How much bombing time results if these recommendations are followed
__________days
What would you have recommended to General Kenney
__________ (Northern Route or Split Reconnaissance or Southern Route)
What would you have recommended to the Japanese Commander
__________ (Northern Route or Southern Route)
How much bombing time results if these recommendations are followed
__________days

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
63
When you bet on a racehorse with odds of m-n, you stand to win m dollars for every bet of n dollars if your horse wins; for instance, if the horse you bet is running at 5-2 and wins, you will win $5 for every $2 you bet. (Thus a $2 bet will return $7.). Here are some actual odds from a 1992 race at Belmont Park, NY. The favorite at 4-1 was Pleasant Tap. The second choice was Thunder Rumble at 7-2, while the third choice was Strike the Gold at 7-2. Assume you are making a $20 bet on one of these horses. The payoffs are your winnings. (If your horse does not win, you lose your entire bet. Of course, it is possible for none of your horses to win.) Suppose that just before the race, there has been frantic betting on Thunder Rumble, with the result that the odds have dropped to 1-5. The odds on the other two horses remain unchanged. Set up the payoff matrix with your bet as the row player and winner as the column player.
Let the first column correspond to Pleasant Tap, the second one to Thunder Rumble, the third one to Strike the Gold and the first row correspond to Pleasant Tap, the second one to Thunder Rumble, the third one to Strike the Gold .
Let the first column correspond to Pleasant Tap, the second one to Thunder Rumble, the third one to Strike the Gold and the first row correspond to Pleasant Tap, the second one to Thunder Rumble, the third one to Strike the Gold .

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
64
Which of the following is a true statement
A)If A and C are matrices and , then .
B) Given , if , then M has an inverse.
C) If A, X, and C are matrices, and , then .
D) If A and C are matrices and , then and if A, X, and C are matrices, and , then is true.
E) None of these statements is true.
A)If A and C are matrices and , then .
B) Given , if , then M has an inverse.
C) If A, X, and C are matrices, and , then .
D) If A and C are matrices and , then and if A, X, and C are matrices, and , then is true.
E) None of these statements is true.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
65
A farmer has a choice of growing wheat, barley, or rice. Her success will depend on the weather, which could be dry, average, or wet. Her payoff matrix is as follows.
If the probability that the weather will be dry is 20%, the probability that it will be average is 60%, and the probability that it will be wet is 20%, what is the farmer's best choice of crop
If the probability that the weather will be dry is 20%, the probability that it will be average is 60%, and the probability that it will be wet is 20%, what is the farmer's best choice of crop

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
66
Use matrix inversion to solve the given system of linear equations.
A) ,
B) ,
C) ,
D) ,
E) The system is inconsistent.
A) ,
B) ,
C) ,
D) ,
E) The system is inconsistent.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
67
Use matrix inversion to solve the system of linear equations.
A) , ,
B) , ,
C) , ,
D) , ,
E) The system is inconsistent.
A) , ,
B) , ,
C) , ,
D) , ,
E) The system is inconsistent.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
68
A manufacturer of electrical machinery is located in a cramped, though low-rent, factory close to the center of a large city. The firm needs to expand, and it could do so in one of three ways: (1) remain where it is and install new equipment, (2) move to a suburban site in the same city, or (3) relocate in a different part of the country where labor is cheaper. Its decision will be influenced by the fact that one of the following will happen: (I) the government may introduce a program of equipment grants, (II) a new suburban highway may be built, or (III) the government may institute a policy of financial help to companies who move into regions of high unemployment. The value to the company of each combination is given in the following payoff matrix.
If the manufacturer judges that there is a 10% probability that the government will go with option I, a 10% probability that they will go with option II, and a 80% probability that they will go with option III, what is the manufacturer's best option
If the manufacturer judges that there is a 10% probability that the government will go with option I, a 10% probability that they will go with option II, and a 80% probability that they will go with option III, what is the manufacturer's best option

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
69
Use row reduction to find the inverse of the given matrix, if it exists. Check your answers by multiplication.
A)
B)
C)
D)
E) The inverse matrix does not exist.
A)
B)
C)
D)
E) The inverse matrix does not exist.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
70
Use the row reduction method to find the inverse, if it exists.
A)
B)
C)
D)
E) no inverse exists
A)
B)
C)
D)
E) no inverse exists

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
71
Decide whether the game is strictly determined. __________ (answer strictly determined or not strictly determined)
If it is, what are the players' optimal pure strategies
A __________
B __________
What is the value of the game __________
If it is, what are the players' optimal pure strategies
A __________
B __________
What is the value of the game __________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
72
Determine which pair of matrices is an inverse pair.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
73
Compute the determinant of the given matrix.
A)26
B) -10
C) 25
D) -1
E) 1
A)26
B) -10
C) 25
D) -1
E) 1

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
74
Your fast-food outlet, Burger Queen, has obtained a license to open branches in three closely situated South African cities: Brakpan, Nigel, and Springs. Your market surveys show that Brakpan and Nigel each provide a potential market of 2,500 burgers a day, while Springs provides a potential market of 1,000 burgers per day. Your company can only finance an outlet in one of those cities at the present time. Your main competitor, Burger Princess, has also obtained licenses for these cities, and is similarly planning to open only one outlet. If you both happen to locate at the same city, you will share the total business from all three cities equally, but if you locate in different cities, you will each get all the business in the cities in which you have located, plus half the business in the third city. The payoff is the number of burgers you will sell per day minus the number of burgers your competitor will sell per day. Set up the payoff matrix with you as the row player and your opponent as the column player.
Let the first column correspond to Brakpan, the second one to Nigel, the third one to Springs and the first row correspond to the Brakpan, the second one to the Nigel, the third one to Springs.
Let the first column correspond to Brakpan, the second one to Nigel, the third one to Springs and the first row correspond to the Brakpan, the second one to the Nigel, the third one to Springs.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
75
Use row reduction to find the inverse of the given matrix, if it exists. Check your answer by multiplication.
A)
B)
C)
D)
E) The inverse matrix does not exist.
A)
B)
C)
D)
E) The inverse matrix does not exist.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
76
Decide whether the game is strictly determined.
__________ (strictly determined or not strictly determined)
If it is, what are the players' optimal pure strategies
A __________
B __________
What is the value of the game __________
__________ (strictly determined or not strictly determined)
If it is, what are the players' optimal pure strategies
A __________
B __________
What is the value of the game __________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
77
You and your friend have come up with the following simple game to pass the time: at each round, you simultaneously call "heads" or "tails". If you have both called the same thing, your friend wins one point; if your calls differ, you win one point. Set up the payoff matrix with you as the row player and your friend as the column player.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
78
Decide whether the game is strictly determined. __________ (answer strictly determined or not strictly determined)
If it is, what are the players' optimal pure strategies
A __________
B __________
What is the value of the game __________
If it is, what are the players' optimal pure strategies
A __________
B __________
What is the value of the game __________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
79
You are deciding whether to invade Japan, Sweden or Canada, and your opponent is simultaneously deciding which of these three countries to defend. If you invade a country that your opponent is defending, you will be defeated (payoff: -2), but if you invade a country your opponent is not defending, you will be successful (payoff: +2). Set up the payoff matrix with you as the row player and your opponent as the column player.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
80
Find the inverse of the given matrix, if it exists.
A)
B)
C)
D)
E) The inverse matrix does not exist.
A)
B)
C)
D)
E) The inverse matrix does not exist.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck


