Deck 15: Inference About Population Variances
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 15: Inference About Population Variances
1
The value of 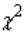 with
with 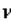 degrees of freedom, such that the area to its left under the chi-squared curve is equal to A, is denoted by
degrees of freedom, such that the area to its left under the chi-squared curve is equal to A, is denoted by 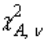 , while
, while 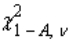 denotes the value such that the area to its right is A.
denotes the value such that the area to its right is A.
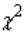 with
with 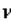 degrees of freedom, such that the area to its left under the chi-squared curve is equal to A, is denoted by
degrees of freedom, such that the area to its left under the chi-squared curve is equal to A, is denoted by 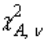 , while
, while 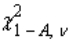 denotes the value such that the area to its right is A.
denotes the value such that the area to its right is A.False
2
Which of the following statements is false?
A) The chi-squared distribution is positively skewed.
B) The chi-squared distribution is symmetrical.
C) All the values of the chi-squared distribution are positive.
D) The shape of the chi-squared distribution depends on the number of degrees of freedom.
A) The chi-squared distribution is positively skewed.
B) The chi-squared distribution is symmetrical.
C) All the values of the chi-squared distribution are positive.
D) The shape of the chi-squared distribution depends on the number of degrees of freedom.
B
3
Which of the following best describes the number of degrees of freedom used in a Chi-square test for a value of the population variance?A.n − 2B.n - kC.n − 1D.n
C
4
Which of the following best describes the Chi-square distribution?A.The Chi-square distribution is continuous B.The Chi-square distribution is positively skewed
CThe Chi-square distribution is used in statistical inference of the population variance
DAll of these choices are correct.
CThe Chi-square distribution is used in statistical inference of the population variance
DAll of these choices are correct.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
In testing for the equality of two population variances, when the populations are normally distributed, the 10% level of significance has been used. To determine the rejection region, it will be necessary to refer to the F table corresponding to an upper-tail area of:
A) 0.90.
B) 0.05.
C) 0.20.
D) 0.10.
A) 0.90.
B) 0.05.
C) 0.20.
D) 0.10.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
A study wants to investigate whether the population variance is greater than 8, if a random sample of size 40, yielded a variance of 10. Which of the following is the correct value of the test statistic?A.50B.1.25C.48.75D.31.2

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
A study wants to investigate whether the population variance is greater than 8, if a random sample of size 40, yielded a variance of 10. Which of the following are the correct null hypothesis and alternative hypotheses?A.Ho: σ2 = 10 HA: σ2 > 10B.Ho: s2 = 10
HA: s2 > 10C.Ho: s2 = 8
HA: s2 > 8D.Ho: σ2 = 8
HA: σ2 > 8
HA: s2 > 10C.Ho: s2 = 8
HA: s2 > 8D.Ho: σ2 = 8
HA: σ2 > 8

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is the most common null hypothesis used when testing for equality of two population variances?A.Ho: σ12/σ22 > 1B.Ho: σ12/σ22 < 1C.Ho: σ12/σ22 = 1D.None of these choices are correct.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
How many degrees of freedom are used for an F statistic?A.(n1 − 1) ×(n2 - 1)B.n − 5C.n − 2D.None of these choices are correct.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
Random samples from two normal populations produced the following statistics: s1 = 3 n1=30
S2 = 4 n2=30
What is the value of the test statistic if we wanted to test the hypothesis that the two populations differ?A.0.750B.1.333C.1.778D.0.563
S2 = 4 n2=30
What is the value of the test statistic if we wanted to test the hypothesis that the two populations differ?A.0.750B.1.333C.1.778D.0.563

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following statements is correct regarding the percentile points of the chi-squared distribution?
A)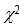 0.99,12 = 26.2170
0.99,12 = 26.2170
B) 11ef1ab3_92d1_8f9f_a741_093cd8e6d188_TB5762_110.95,12 = 0.102587.
C) 11ef1ab3_92d1_8f9f_a741_093cd8e6d188_TB5762_110.95,12 = 28.2995.
D) 11ef1ab3_92d1_8f9f_a741_093cd8e6d188_TB5762_110.99,12 = 3.57056.
A)
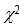 0.99,12 = 26.2170
0.99,12 = 26.2170B) 11ef1ab3_92d1_8f9f_a741_093cd8e6d188_TB5762_110.95,12 = 0.102587.
C) 11ef1ab3_92d1_8f9f_a741_093cd8e6d188_TB5762_110.95,12 = 28.2995.
D) 11ef1ab3_92d1_8f9f_a741_093cd8e6d188_TB5762_110.99,12 = 3.57056.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following statements is correct regarding the percentile points of the F-distribution?
A)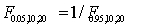 .
.
B)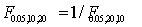 .
.
C)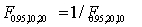 .
.
D)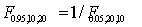 .
.
A)
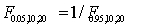 .
.B)
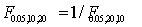 .
.C)
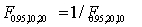 .
.D)
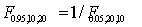 .
.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following statements is not correct for an F-distribution?
A) Variables that are F-distributed range from 0 to .
B) The exact shape of the distribution is determined by two numbers of degrees of freedom.
C) The number of degrees of freedom for the denominator is always smaller than the number of degrees of freedom for the numerator.
D) The number of degrees of freedom for the numerator can be larger than, smaller than, or equal to the number of degrees of freedom for the denominator.
A) Variables that are F-distributed range from 0 to .
B) The exact shape of the distribution is determined by two numbers of degrees of freedom.
C) The number of degrees of freedom for the denominator is always smaller than the number of degrees of freedom for the numerator.
D) The number of degrees of freedom for the numerator can be larger than, smaller than, or equal to the number of degrees of freedom for the denominator.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
The ratio of two independent chi-squared variables, each divided by its number of degrees of freedom, is:
A) normally distributed.
B) Student t distributed.
C) chi-squared distributed.
D) F distributed.
A) normally distributed.
B) Student t distributed.
C) chi-squared distributed.
D) F distributed.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
In constructing a 95% interval estimate for the ratio of two population variances, 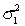 /
/ 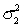 , two independent samples of sizes 41 and 61 are drawn from the populations. If the sample variances are 515 and 920, then the upper confidence limit is:
, two independent samples of sizes 41 and 61 are drawn from the populations. If the sample variances are 515 and 920, then the upper confidence limit is:
A) 0.321.
B) 1.009.
C) 0.311.
D) 0.974.
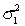 /
/ 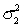 , two independent samples of sizes 41 and 61 are drawn from the populations. If the sample variances are 515 and 920, then the upper confidence limit is:
, two independent samples of sizes 41 and 61 are drawn from the populations. If the sample variances are 515 and 920, then the upper confidence limit is:A) 0.321.
B) 1.009.
C) 0.311.
D) 0.974.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following best describes the sampling distribution of s12/s22 , if we have independently sampled from two normal populations?A.Z distributionB.t distributionC.Chi square distributionD.F distribution

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following is the test statistic for σ2?A.Z test statisticB.χ2 test statisticC.t test statisticD.None of these choices are correct

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
The F-distribution is the sampling distribution of the ratio of:
A) two normal population variances.
B) two normal population means.
C) two sample variances, provided that the samples are independently drawn from two normal populations.
D) two sample variances, provided that the sample sizes are large.
A) two normal population variances.
B) two normal population means.
C) two sample variances, provided that the samples are independently drawn from two normal populations.
D) two sample variances, provided that the sample sizes are large.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
The sampling distribution of the ratio of two sample variances 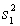 /
/ 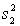 is said to be F-distributed provided that:
is said to be F-distributed provided that:
A) the samples are independent.
B) the populations are normal with equal variances.
C) the samples are dependent and their sizes are large.
D) the samples are independently drawn from two normal populations.
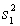 /
/ 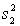 is said to be F-distributed provided that:
is said to be F-distributed provided that:A) the samples are independent.
B) the populations are normal with equal variances.
C) the samples are dependent and their sizes are large.
D) the samples are independently drawn from two normal populations.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
Two independent samples are drawn from two normal populations, where the population variances are assumed to be equal. The sampling distribution of the ratio of the two sample variances is:
A) a normal distribution.
B) Student t-distribution.
C) an F-distribution.
D) a chi-squared distribution.
A) a normal distribution.
B) Student t-distribution.
C) an F-distribution.
D) a chi-squared distribution.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
The value in a chi-squared distribution with 4 degrees of freedom such that the area to its right is 0.99 is 0.29711.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
When the necessary conditions are met, a two-tail test is being conducted at 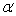 = 0.05 to test
= 0.05 to test 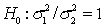 . The two sample variances are
. The two sample variances are 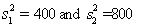 , and the sample sizes are
, and the sample sizes are 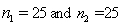 . The calculated value of the test statistic will be F = 2.
. The calculated value of the test statistic will be F = 2.
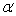 = 0.05 to test
= 0.05 to test 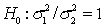 . The two sample variances are
. The two sample variances are 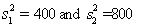 , and the sample sizes are
, and the sample sizes are 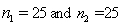 . The calculated value of the test statistic will be F = 2.
. The calculated value of the test statistic will be F = 2.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
We define 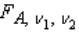 as the value of the F with
as the value of the F with 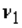 and
and 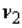 degrees of freedom such that the area to its left under the F curve is A, while
degrees of freedom such that the area to its left under the F curve is A, while 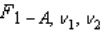 is defined as the value such that the area to its left is A.
is defined as the value such that the area to its left is A.
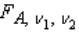 as the value of the F with
as the value of the F with 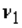 and
and 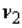 degrees of freedom such that the area to its left under the F curve is A, while
degrees of freedom such that the area to its left under the F curve is A, while 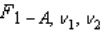 is defined as the value such that the area to its left is A.
is defined as the value such that the area to its left is A.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
The value in an F-distribution with 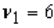 and
and 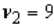 degrees of freedom such that the area to its right is 0.05 is 3.37.
degrees of freedom such that the area to its right is 0.05 is 3.37.
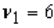 and
and 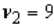 degrees of freedom such that the area to its right is 0.05 is 3.37.
degrees of freedom such that the area to its right is 0.05 is 3.37.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
Random samples from two normal populations produced the following statistics: 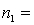 25,
25, 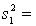 75.
75. 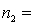 13,
13, 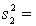 130.
130.
Briefly describe the 95% confidence the ratio of the two population variances:
LCL = (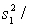
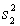 ) / F0.025,24,12 = 0.191.
) / F0.025,24,12 = 0.191.
UCL = (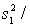
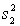 )F0.025,12,24 = 1.465.
)F0.025,12,24 = 1.465.
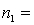 25,
25, 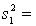 75.
75. 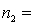 13,
13, 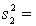 130.
130.Briefly describe the 95% confidence the ratio of the two population variances:
LCL = (
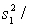
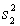 ) / F0.025,24,12 = 0.191.
) / F0.025,24,12 = 0.191.UCL = (
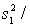
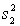 )F0.025,12,24 = 1.465.
)F0.025,12,24 = 1.465.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
The value in an F-distribution with 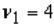 and
and 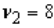 degrees of freedom such that the area to its left is 0.975 is 5.05.
degrees of freedom such that the area to its left is 0.975 is 5.05.
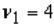 and
and 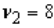 degrees of freedom such that the area to its left is 0.975 is 5.05.
degrees of freedom such that the area to its left is 0.975 is 5.05.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
The value in a chi-squared distribution with 5 degrees of freedom such that the area to its right is 0.10 is 1.61031.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
To find the value in a chi-squared distribution with 10 degrees of freedom such that the area to its left is 0.01, we find the point in the same distribution such that the area to its left is 0.99.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
Random samples from two normal populations produced the following statistics: 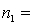 25,
25, 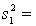 75.
75. 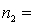 13,
13, 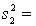 130.
130.
Estimate with 95% confidence the ratio of the two population variances.
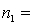 25,
25, 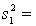 75.
75. 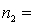 13,
13, 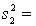 130.
130.Estimate with 95% confidence the ratio of the two population variances.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
The value in an F-distribution with 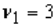 and
and 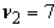 degrees of freedom such that the area to its left is 0.99 is 0.036.
degrees of freedom such that the area to its left is 0.99 is 0.036.
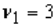 and
and 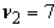 degrees of freedom such that the area to its left is 0.99 is 0.036.
degrees of freedom such that the area to its left is 0.99 is 0.036.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
A university lecturer wants to investigate if the variance of final marks of students in two of her courses differs. She takes a random sample of 25 students from the mathematics course she lectures and finds the student's final marks had a variance of 5. She takes a random sample of 13 students from the statistics course she lectures and finds the variance of 10. Assuming that the final grades of students in her mathematics and in her statistics course are normally distributed, is there enough evidence at the 5% significance level for this lecturer to infer that the two population variances differ?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
When the necessary conditions are met, a two-tail test is being conducted at 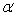 = 0.05 to test
= 0.05 to test 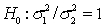 . The two sample variances are
. The two sample variances are 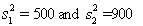 , and the sample sizes are
, and the sample sizes are 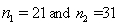 . The rejection region is F > 2.20 or F < 0.4255.
. The rejection region is F > 2.20 or F < 0.4255.
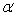 = 0.05 to test
= 0.05 to test 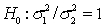 . The two sample variances are
. The two sample variances are 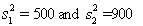 , and the sample sizes are
, and the sample sizes are 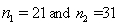 . The rejection region is F > 2.20 or F < 0.4255.
. The rejection region is F > 2.20 or F < 0.4255.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
Random samples from two normal populations produced the following statistics: 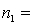 25,
25, 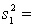 75.
75. 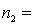 13,
13, 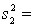 130.
130.
Briefly explain how to use the 95% confidence the ratio of the two population variances to test the hypothesis of equal population variances.
LCL = (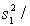
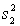 ) / F0.025,24,12 = 0.191.
) / F0.025,24,12 = 0.191.
UCL = (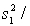
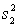 )F0.025,12,24 = 1.465.
)F0.025,12,24 = 1.465.
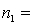 25,
25, 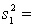 75.
75. 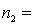 13,
13, 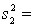 130.
130.Briefly explain how to use the 95% confidence the ratio of the two population variances to test the hypothesis of equal population variances.
LCL = (
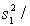
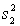 ) / F0.025,24,12 = 0.191.
) / F0.025,24,12 = 0.191.UCL = (
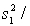
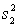 )F0.025,12,24 = 1.465.
)F0.025,12,24 = 1.465.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
The test statistic employed to test 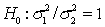 is
is 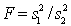 , which is F-distributed with
, which is F-distributed with 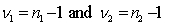 degrees of freedom, provided that the two populations are F-distributed.
degrees of freedom, provided that the two populations are F-distributed.
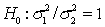 is
is 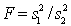 , which is F-distributed with
, which is F-distributed with 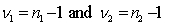 degrees of freedom, provided that the two populations are F-distributed.
degrees of freedom, provided that the two populations are F-distributed.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
When comparing two population variances, we use the difference 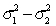 rather than the ratio
rather than the ratio 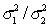 .
.
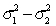 rather than the ratio
rather than the ratio 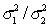 .
.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
The value in a chi-squared distribution with 8 degrees of freedom such that the area to its left is 0.95 is 15.5073.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
The value in an F-distribution with 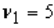 and
and 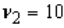 degrees of freedom such that the area to its left is 0.95 is 4.74.
degrees of freedom such that the area to its left is 0.95 is 4.74.
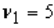 and
and 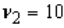 degrees of freedom such that the area to its left is 0.95 is 4.74.
degrees of freedom such that the area to its left is 0.95 is 4.74.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
Random samples from two normal populations produced the following statistics: 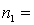 10,
10, 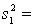 40.
40. 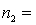 15,
15, 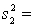 20.
20.
Is there enough evidence at the 5% significance level to infer that the variance of population 1 is larger than the variance of population 2?
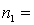 10,
10, 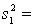 40.
40. 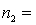 15,
15, 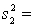 20.
20.Is there enough evidence at the 5% significance level to infer that the variance of population 1 is larger than the variance of population 2?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
The value in a chi-squared distribution with 6 degrees of freedom such that the area to its left is 0.05 is 12.5916.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
A statistician wants to test for the equality of means in two independent samples drawn from normal populations. However, he will not perform the equal-variance t-test of the difference between the population means if the condition necessary for its use is not satisfied. The data are as follows:  Given the data above, can the statistician conclude at the 5% significance level that the required condition is not satisfied?
Given the data above, can the statistician conclude at the 5% significance level that the required condition is not satisfied?
 Given the data above, can the statistician conclude at the 5% significance level that the required condition is not satisfied?
Given the data above, can the statistician conclude at the 5% significance level that the required condition is not satisfied?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
What are the rejection regions for each of the following sets of hypotheses?
a. Ho: σ12/σ22 = 1
HA: σ12/σ22 ≠ 1
n1 = 9 n2 = 20 α = 0.05
b. Ho: σ12/σ22 = 1
HA: σ12/σ22 < 1
n1 = 40 n2 = 50 α = 0.10
c. Ho: σ12/σ22 = 1
HA: σ12/σ22 > 1
n1 = 10 n2 = 8 α = 0.01
a. Ho: σ12/σ22 = 1
HA: σ12/σ22 ≠ 1
n1 = 9 n2 = 20 α = 0.05
b. Ho: σ12/σ22 = 1
HA: σ12/σ22 < 1
n1 = 40 n2 = 50 α = 0.10
c. Ho: σ12/σ22 = 1
HA: σ12/σ22 > 1
n1 = 10 n2 = 8 α = 0.01

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
A statistician wants to test for the equality of means in two independent samples drawn from normal populations. However, he will not perform the equal-variance t-test of the difference between the population means if the condition necessary for its use is not satisfied. The data are as follows:  Estimate with 95% confidence the ratio of the two population variances.
Estimate with 95% confidence the ratio of the two population variances.
 Estimate with 95% confidence the ratio of the two population variances.
Estimate with 95% confidence the ratio of the two population variances.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
A statistician wants to test for the equality of means in two independent samples drawn from normal populations. However, he will not perform the equal-variance t-test of the difference between the population means if the condition necessary for its use is not satisfied. The data are as follows:  Briefly describe what the interval estimate in the previous question tells you.
Briefly describe what the interval estimate in the previous question tells you.
 Briefly describe what the interval estimate in the previous question tells you.
Briefly describe what the interval estimate in the previous question tells you.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
In a random sample of 20 patients who visited the emergency room of hospital 1, a researcher found that the variance of the waiting time (in minutes) was 128.0. In a random sample of 15 patients in the emergency room of hospital 2, the researcher found the variance to be 178.8.
Can we infer at the 5% level of significance that the population variances differ?
Can we infer at the 5% level of significance that the population variances differ?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
For each of the following hypothesis tests, state for what values of χ2 we would reject Ho.
a. Ho: σ12 = 10
HA: σ12 ≠ 10
α = 0.10 and n = 50
b. Ho: σ12 = 4
HA: σ12 > 4
α = 0.05 and n = 30
c. Ho: σ12 = 0.50
HA: σ12 < 0.50
α = 0.01 and n = 45
a. Ho: σ12 = 10
HA: σ12 ≠ 10
α = 0.10 and n = 50
b. Ho: σ12 = 4
HA: σ12 > 4
α = 0.05 and n = 30
c. Ho: σ12 = 0.50
HA: σ12 < 0.50
α = 0.01 and n = 45

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
In a random sample of 20 patients who visited the emergency room of hospital 1, a researcher found that the variance of the waiting time (in minutes) was 128.0. In a random sample of 15 patients in the emergency room of hospital 2, the researcher found the variance to be 178.8.
Estimate with 95% confidence the ratio of the two population variances.
Estimate with 95% confidence the ratio of the two population variances.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
In a random sample of 20 patients who visited the emergency room of hospital 1, a researcher found that the variance of the waiting time (in minutes) was 128.0. In a random sample of 15 patients in the emergency room of hospital 2, the researcher found the variance to be 178.8.
Briefly describe what the interval estimate in the previous question tells you.
Briefly describe what the interval estimate in the previous question tells you.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
An investor is considering two types of investment. She is quite satisfied that the expected return on investment 1 is higher than the expected return on investment 2. However, she is quite concerned that the risk associated with investment 1 is higher than that of investment 2. To help make her decision, she randomly selects seven monthly returns on investment 1 and ten monthly returns on investment 2. She finds that the sample variances of investments 1 and 2 are 225 and 118, respectively.
Estimate with 95% confidence the ratio of the two population variances, and briefly describe what the interval estimate tells you.
Estimate with 95% confidence the ratio of the two population variances, and briefly describe what the interval estimate tells you.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
An investor is considering two types of investment. She is quite satisfied that the expected return on investment 1 is higher than the expected return on investment 2. However, she is quite concerned that the risk associated with investment 1 is higher than that of investment 2. To help make her decision, she randomly selects seven monthly returns on investment 1 and 10 monthly returns on investment 2. She finds that the sample variances of investments 1 and 2 are 225 and 118, respectively.
Can she infer at the 5% significance level that the population variance of investment 1 exceeds that of investment 2?
Can she infer at the 5% significance level that the population variance of investment 1 exceeds that of investment 2?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


