Deck 6: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/106
Play
Full screen (f)
Deck 6: Probability
1
If you roll a fair (unbiased) die 60 times, you should expect an odd number to appear: 

B
2
If the events A and B are independent, with P(A) = 0.30 and P(B) = 0.40, then the probability that both events will occur simultaneously is: 

B
3
Two events A and B are said to be independent if: 

D
4
Suppose P(A) = 0.25. The probability of complement of A is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
5
An experiment consists of three stages. There are two possible outcomes in the first stage, three possible outcomes in the second stage, and four possible outcomes in the third stage. Drawing a tree diagram for this experiment will show that the total number of outcomes is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
6
An approach of assigning probabilities that assumes that all outcomes of the experiment are equally likely is referred to as the: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
7
If P(A) = 0.60, P(B) = 0.58, and P(A B) = 0.70, then P(A \ B) is:

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
8
An experiment consists of tossing three unbiased coins simultaneously. Drawing a probability tree for this experiment will show that the number of simple events in this experiment is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
9
The collection of all possible outcomes of an experiment is called: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
10
If P(A) = 0.20, P(B) = 0.30 and P(A \ B) = 0.00, then A and B are:
A) dependent events.
B) independent events.
C) mutually exclusive events.
D) complementary events.
A) dependent events.
B) independent events.
C) mutually exclusive events.
D) complementary events.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
11
Two events A and B are said to mutually exclusive if: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following is not an approach to assigning probabilities? 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
13
When a fair die is rolled once, the sample space consists of the following six outcomes: 1, 2, 3, 4, 5, 6. Given this sample space, which of the following is a simple event? 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following statements is always correct? 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following is a requirement of the probabilities assigned to the outcomes 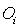 ?
? 
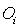 ?
? 

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
16
If P(A) = 0.35, P(B) = 0.45 and P(A \ B) =0.20, then P(A | B) is:

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
17
If A and B are mutually exclusive events with P(A) = 0.80, then P(B): 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
18
A useful graphical method of constructing the sample space for an experiment is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
19
If P(A) = 0.65, P(B) =0.76 and P(A \ B) =0.80, then P(A B) is:

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
20
If A and B are independent events with P(A) = 0.60 and P(A/B) = 0.60, then P(B) is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
21
The annual estimate of the number of deaths of infants is an example of the classical approach to probability.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
22
The probability of event A and event B occurring must be equal to 1.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
23
If A and B are mutually exclusive events, with P(A) = 0.30 and P(B) = 0.40, then P(A B) is:
A) .
B) .
C) .
D) None of these choices are correct.
A) .
B) .
C) .
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
24
If an experiment consists of five outcomes, with 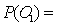 0.10,
0.10, 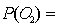 0.10,
0.10, 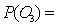 0.30,
0.30, 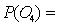 0.25, then
0.25, then 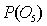 is:
is: 
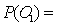 0.10,
0.10, 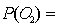 0.10,
0.10, 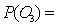 0.30,
0.30, 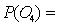 0.25, then
0.25, then 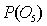 is:
is: 

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
25
Based on past exam results in principles of accounting you estimate that there is an 83% chance of passing the exam. This is an example of the subjective approach to probability.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
26
Two or more events are said to be independent when the occurrence of one event has an effect on the probability that another will occur.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
27
If we wished to determine the probability that one or more of several events will occur in an experiment, we would use addition rules.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
28
If A and B are independent events, with P(A) = 0.50 and P(B) = 0.70, then the probability that A occurs or B occurs or both occur is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
29
If event A does not occur, then its complement 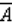 must occur.
must occur.
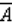 must occur.
must occur.
Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
30
If a coin is tossed three times, and a statistician predicts that the probability of obtaining three heads in a row is 0.125, which of the following assumptions is irrelevant to his prediction? 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
31
Probability refers to a number between 0 and 1 (inclusive), which expresses the chance that an event will occur.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
32
If the event of interest is A, the probability that A will not occur is the complement of A.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
33
If P(A) = 0.25 and P(B) = 0.65, then P(A B) is:
A) .
B) .
C) .
D) cannot be determined from the information given.
A) .
B) .
C) .
D) cannot be determined from the information given.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
34
Marginal probability is the probability that a given event will occur, with no other events taken into consideration.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
35
If A and B are independent events, with P(A) = 0.20 and P(B) =0.60, then P(A | B) is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
36
The classical approach to assigning probability can be applied for experiments that have equally likely outcomes.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
37
Conditional probability is the probability that an event will occur, given that another event will also occur.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
38
The relative frequency approach to probability depends on the law of large numbers.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
39
Of the last 400 customers entering a supermarket, 20 have purchased a mobile phone. If the classical approach for assigning probabilities is used, the probability that the next customer will purchase a mobile phone is: 


Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
40
If A and B are mutually exclusive events, with P(A) = 0.20 and P(B) = 0.30, then P(A \ B) is:

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
41
Jim and John go to a coffee shop during their lunch break and toss a coin to see who will pay. The probability that John will pay three days in a row is 0.125.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
42
Bayes' theorem allows us to compute conditional probabilities from other forms of probability.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
43
Two events A and B are said to be independent if P(A \B) = P(A) + P(B).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
44
If events A and B have nonzero probabilities, then they can be both independent and mutually exclusive.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
45
When it is not reasonable to use the classical approach to assigning probabilities to the outcomes of an experiment, and there is no history of the outcomes, we have no alternative but to employ the subjective approach.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
46
Three candidates for the presidency of a university's student union, Alice, Brenda and Cameron, are to address a student forum. The forum's organiser is to select the order in which the candidates will give their speeches, and must do so in such a way that each possible order is equally likely to be selected.
a. What is the random experiment?
b. List the simple events in the sample space.
c. Assign probabilities to the simple events.
d. What is the probability that Cameron will speak first?
e. What is the probability that one of the women will speak first?
f. What is the probability that Alice will speak before Cameron does?
a. What is the random experiment?
b. List the simple events in the sample space.
c. Assign probabilities to the simple events.
d. What is the probability that Cameron will speak first?
e. What is the probability that one of the women will speak first?
f. What is the probability that Alice will speak before Cameron does?

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
47
The probability of the union of two mutually exclusive events A and B is P(A B) = P(A) + P(B).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
48
Given that events A and B are independent, and that P(A) = 0.9 and P(B | A) = 0.5, then P(A \ B) = 0.45.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
49
There are three approaches to determining the probability that an outcome will occur: the classical, relative frequency, and subjective approaches. Which is most appropriate in determining the probability of the following outcomes?
a. A flipped coin will land on tails.
b. The probability of your favourite team winning the finals.
c. Five of the next 20 new cars sold in Adelaide will be imported cars.
a. A flipped coin will land on tails.
b. The probability of your favourite team winning the finals.
c. Five of the next 20 new cars sold in Adelaide will be imported cars.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
50
An effective and simple method of applying the probability rules is the probability tree, wherein the events of an experiment are represented by lines.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
51
Assume that A and B are independent events, with P(A) = 0.30 and P(B) = 0.50. The probability that both events will occur simultaneously is 0.80.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose A and B are two independent events, with P(A) = 0.20 and P(B) = 0.60.
a. Find P(B | A).
b. Find P(A | B).
c. Find P(A and B).
d. Find P(A or B).
a. Find P(B | A).
b. Find P(A | B).
c. Find P(A and B).
d. Find P(A or B).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
53
An experiment consists of tossing three fair (unbiased) coins simultaneously. This experiment has eight possible outcomes.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
54
Baye' Law is a method of revising probabilities after another event has occurred.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
55
According to an old song lyric, 'love and marriage go together like a horse and carriage'. Let love be event A and marriage be event B. Events A and B cannot be mutually exclusive.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
56
Two events A and B are said to mutually exclusive if P(A) = P(B).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
57
When events are mutually exclusive, they can happen at the same time.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
58
The relative frequency approach is not useful in interpreting probability statements such as those heard from weather forecasters or scientists.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
59
If A and B are independent events, with P(A) = 0.30 and P(B) = 0.50, then P(B | A) is 0.10.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
60
Five students from a statistics class have formed a study group. Each may or may not attend a study session. Assuming that the members will be making independent decisions on whether or not to attend, there are 32 different possibilities for the composition of the study session.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
61
A statistics professor classifies his students according to their gender and the number of hours of paid work they do a week. The following table gives the proportions of students falling into the various categories. One student is selected at random.
Paid Work (hours/week) a. If the student selected is female, what is the probability that he works between 1 and 8 hours a week?
b. If the selected student works more than 16 hours a week, what is the probability that the student is male?
c. What is the probability that the student selected is female or does do any paid work or both?
d. Is gender independent of the number of hours of paid work done a week? Explain using probabilities.
Paid Work (hours/week) a. If the student selected is female, what is the probability that he works between 1 and 8 hours a week?
b. If the selected student works more than 16 hours a week, what is the probability that the student is male?
c. What is the probability that the student selected is female or does do any paid work or both?
d. Is gender independent of the number of hours of paid work done a week? Explain using probabilities.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
62
An ice cream vendor sells three flavours: chocolate, strawberry and vanilla. 45% of the sales are chocolate, 30% are strawberry and the rest are vanilla. Sales are by the cone or the cup. The percentages of cones sales for chocolate, strawberry and vanilla are 75%, 60% and 40%, respectively. For a randomly selected sale, define the following events:
A1 = chocolate chosen.
A2 = strawberry chosen.
A3 = vanilla chosen.
B = ice cream in a cone. = ice cream in a cup.
Use this information to answer the following question(s).
-Find the probability that the ice cream was sold on a cone and the flavour was:
a. chocolate.
b. strawberry.
c. vanilla.
A1 = chocolate chosen.
A2 = strawberry chosen.
A3 = vanilla chosen.
B = ice cream in a cone. = ice cream in a cup.
Use this information to answer the following question(s).
-Find the probability that the ice cream was sold on a cone and the flavour was:
a. chocolate.
b. strawberry.
c. vanilla.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
63
A survey of a magazine's subscribers indicates that 40% own a home, 80% own a car, and 90% of the homeowners who subscribe also own a car. What proportion of subscribers:
a. own both a car and a house?
b. own a car or a house, or both?
c. own neither a car nor a house?
a. own both a car and a house?
b. own a car or a house, or both?
c. own neither a car nor a house?

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
64
Suppose P(A) = 0.40, P(B) = 0.50, and P(A B) = 0.70.
a. Find P(A B).
b. Find P(B | A).
c. Are A and B independent events? Explain using probabilities.
a. Find P(A B).
b. Find P(B | A).
c. Are A and B independent events? Explain using probabilities.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
65
Suppose P(A) = 0.30, P(B) = 0.40, and P(B /A) = 0.60.
a. Find P(A B).
b. Find P(A B).
c. Find P(A /B).
a. Find P(A B).
b. Find P(A B).
c. Find P(A /B).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
66
A woman is expecting her second child. Her doctor has told her that she has a 50-50 chance of having another girl. If she has another girl, there is a 90% chance that she will be taller than the first. If she has a boy, however, there is only a 25% chance that he will be taller than the first child. Find the probability that the woman's second child will be taller than the first.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
67
An insurance company has recently recruited ten graduates, four men and six women. Two of the graduates are to be selected at random to work in the firm's suburban office.
a. What is the probability that two men will be selected?
b. What is the probability that at least one man will be selected?
a. What is the probability that two men will be selected?
b. What is the probability that at least one man will be selected?

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
68
An financial advisor tells you that in her estimation there is an 85% chance that a particular stock's price will increase over the next three weeks.
a. Which approach was used to produce this figure?
b. Interpret the 85% probability.
a. Which approach was used to produce this figure?
b. Interpret the 85% probability.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
69
Suppose P( ) = 0.10, P( | A) = 0.40, and P( | ) = 0.50.
a. Find P(A).
b. Find P( \A).
c. Find P( \ ).
a. Find P(A).
b. Find P( \A).
c. Find P( \ ).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
70
The sample space of the toss of a fair die is S = {1, 2, 3, 4, 5, 6}. If the die is balanced, each simple event has the same probability. Find the probability of the following events.
a. Equal to 1.
b. A number greater than 3.
c. A number greater than 6.
d. A number between 2 and 4, inclusive.
a. Equal to 1.
b. A number greater than 3.
c. A number greater than 6.
d. A number between 2 and 4, inclusive.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
71
Is it possible to have two events for which P(A) = 0.40, P(B) = 0.50, and P(A B) = 0.20? Explain.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
72
An insurance company has collected the following data on the gender and marital status of 300 customers.
Marital Status Suppose that a customer is selected at random. Find the probability that the customer selected is:
a. a married female.
b. not single.
c. married, if the customer is male.
d. female or divorced.
e. Are gender and marital status mutually exclusive? Explain using probabilities.
f. Is marital status independent of gender? Explain using probabilities.
Marital Status Suppose that a customer is selected at random. Find the probability that the customer selected is:
a. a married female.
b. not single.
c. married, if the customer is male.
d. female or divorced.
e. Are gender and marital status mutually exclusive? Explain using probabilities.
f. Is marital status independent of gender? Explain using probabilities.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
73
A pharmaceutical firm has discovered a new diagnostic test for a certain disease that has infected 1% of the population. The firm has announced that 95% of those infected will show a positive test result, while 98% of those not infected will show a negative test result. What proportion of test results are correct?

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
74
Suppose P(A) = 0.10, P(B | A) = 0.20, and P(B | ) = 0.40.
a. Find P(A B).
b. Are A and B mutually exclusive events?
a. Find P(A B).
b. Are A and B mutually exclusive events?

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
75
The following table shows the numbers of cars sold by a car dealer during the last 30 weeks. 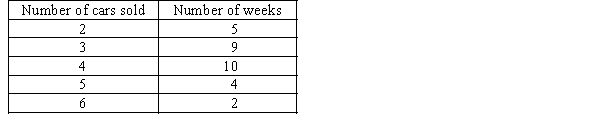 a. Define the random variable of interest to the dealer.
a. Define the random variable of interest to the dealer.
b. List the simple events in the sample space.
c. Assign probabilities to the simple events and show the probability distribution.
d. What approach have you used in determining the probabilities in part (c)?
e. What is the probability of selling no more than four cars in any given week?
 a. Define the random variable of interest to the dealer.
a. Define the random variable of interest to the dealer.b. List the simple events in the sample space.
c. Assign probabilities to the simple events and show the probability distribution.
d. What approach have you used in determining the probabilities in part (c)?
e. What is the probability of selling no more than four cars in any given week?

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
76
Suppose A and B are two mutually exclusive events for which P(A) = 0.25 and P(B) = 0.60.
a. Find P(A B).
b. Find P(A B).
c. Find P(A | B).
d. Are A and B independent events? Explain using probabilities.
a. Find P(A B).
b. Find P(A B).
c. Find P(A | B).
d. Are A and B independent events? Explain using probabilities.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
77
Suppose P(A) = 0.1, P(B) = 0.5, and P(A B) = 0.
a. Find P(A B).
b. Are A and B independent events? Explain.
c. Are A and B mutually exclusive events? Explain.
a. Find P(A B).
b. Are A and B independent events? Explain.
c. Are A and B mutually exclusive events? Explain.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
78
At the beginning of each year, an investment newsletter predicts whether or not the stock market will rise over the coming year. Historical evidence reveals that there is a 75% chance that the stock market will rise in any given year. The newsletter has predicted a rise for 80% of the years when the market actually rose, and has predicted a rise for 40% of the years when the market fell. Find the probability that the newsletter's prediction for next year will be correct.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose P(A) = 0.10, P(B) = 0.70, and P(B/A) = 0.80.
a. Find P(A \ B).
b. Find P(A B).
c. Find P(A | B).
a. Find P(A \ B).
b. Find P(A B).
c. Find P(A | B).

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck
80
Suppose P(A) = 0.50, P(B) = 0.30, and P(A or B) = 0.80.
a. Find P(A B).
b. Find P(B | A).
c. Are A and B mutually exclusive events? Explain using probabilities.
a. Find P(A B).
b. Find P(B | A).
c. Are A and B mutually exclusive events? Explain using probabilities.

Unlock Deck
Unlock for access to all 106 flashcards in this deck.
Unlock Deck
k this deck


