Deck 9: Propositional Logic-Propositions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/223
Play
Full screen (f)
Deck 9: Propositional Logic-Propositions
1
In the statement form p • q, the component statement variables p and q are called:
A)conjuncts
B)disjuncts
C)antecedents
D)consequents
E)There is no special name for the component statements.
A)conjuncts
B)disjuncts
C)antecedents
D)consequents
E)There is no special name for the component statements.
A
2
The connective "•" is called:
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
A
3
The connective "~" is called:
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
B
4
The connective used for conjunctions is:
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
5
The connective used for negations is:
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
6
In the truth table for the statement form ~p, the column of truth values underneath the main connective should be:
A)TF
B)FT
C)TFTF
D)TTFF
E)FFTT
A)TF
B)FT
C)TFTF
D)TTFF
E)FFTT

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
7
The statement form p q is:
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
8
In the truth table for the statement form p q, the column of truth values underneath the main connective should be:
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
9
Symbolize "not both p and q."
A)~p • ~q
B)~p • q
C)~( p • q)
D)( p vq) • ~( p • q)
E)( pv q) • (~p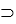 q)
q)
A)~p • ~q
B)~p • q
C)~( p • q)
D)( p vq) • ~( p • q)
E)( pv q) • (~p
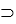 q)
q)
Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
10
The statement form ¬ p is:
A)a negation
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a negation
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
11
The connective used for biconditionals is:
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
12
The statement form p & q is:
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
13
The connective used for disjunctions is:
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
14
Choose which symbol to use for "it is not the case that," "it is false that," and "n't."
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
15
The statement form ~p is:
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
16
Symbolize "both not p and not q."
A)~p • ~q
B)~p • q
C)~( p • q)
D)( p v q) • ~( p • q)
E)( p v q) • (~p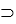 q)
q)
A)~p • ~q
B)~p • q
C)~( p • q)
D)( p v q) • ~( p • q)
E)( p v q) • (~p
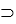 q)
q)
Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
17
Choose which symbol to use for "but," "however," "nevertheless," and "although."
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
18
The statement form p • q is:
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
19
In the truth table for the statement form p • q, the column of truth values underneath the main connective should be:
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
20
The connective used for conditionals is:
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
21
The connective " " is called:
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
22
The statement form p q is:
A)a conjunction
B)a negation
C)a disjunction
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a negation
C)a disjunction
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
23
The connective " " is called:
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
24
The connective " " is called:
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"
A)"dot"
B)"tilde"
C)"wedge"
D)"horseshoe"
E)"triple bar"

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
25
Choose which symbol to use for "provided," "given that," "supposing that," "unless," and "only if."
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
26
Choose which symbol to use for "just in case" and "just in the event that."
A)•
B)~
C)
D)
E)
A)•
B)~
C)
D)
E)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
27
The statement form p q is:
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
28
The statement form p q is:
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
29
In the statement form p q, the component statement variables p and q are called:
A)conjuncts
B)disjuncts
C)antecedents
D)consequents
E)There is no special name for the component statements.
A)conjuncts
B)disjuncts
C)antecedents
D)consequents
E)There is no special name for the component statements.

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
30
The statement form p q is:
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
31
In the statement form p q, the component statement variables p and q are called:
A)conjuncts
B)disjuncts
C)antecedents
D)consequents
E)There is no special name for the component statements.
A)conjuncts
B)disjuncts
C)antecedents
D)consequents
E)There is no special name for the component statements.

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
32
The statement form p q is:
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form
A)a conjunction
B)a negation
C)a disjunction
D)a conditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
33
In the truth table for the statement form p q, the column of truth values underneath the main connective should be:
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
34
The statement form p q is:
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
35
Symbolize "neither p nor q."
A)~p ~q
B)(~p ~q) • (p • q)
C)~( p q)
D)( p q) • ~( p • q)
E)( p q) • (~p q)
A)~p ~q
B)(~p ~q) • (p • q)
C)~( p q)
D)( p q) • ~( p • q)
E)( p q) • (~p q)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
36
In the statement form p q, the component statement variable p is called:
A)the conjunct
B)the disjunct
C)the antecedent
D)the consequent
E)There are no special names for the component statements.
A)the conjunct
B)the disjunct
C)the antecedent
D)the consequent
E)There are no special names for the component statements.

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
37
In the truth table for the statement form p q, the column of truth values underneath the consequent should be:
A)TF
B)TTFF
C)TFTF
D)TTTTFFFF
E)TTFFTTFF
A)TF
B)TTFF
C)TFTF
D)TTTTFFFF
E)TTFFTTFF

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
38
Symbolize "p or q but not both."
A)p q
B)(p q) • (~p • ~q)
C)(p q) • ~(p q)
D)(p q) • ~(p • q)
E)(p q) • (~p q)
A)p q
B)(p q) • (~p • ~q)
C)(p q) • ~(p q)
D)(p q) • ~(p • q)
E)(p q) • (~p q)

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
39
In the truth table for the statement form p q, the column of truth values underneath the main connective should be:
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT
A)TTTF
B)TFFF
C)TFTT
D)TTFF
E)TFFT

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
40
In the truth table for the statement form p q, the column of truth values underneath the antecedent should be:
A)TF
B)TTFF
C)TFTF
D)TTTTFFFF
E)TTFFTTFF
A)TF
B)TTFF
C)TFTF
D)TTTTFFFF
E)TTFFTTFF

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
41
The statement form p q is:
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form
A)a conjunction
B)a disjunction
C)a conditional
D)a biconditional
E)not actually a statement form

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
42
Identify which of the following is a correct symbolization of the following statement. The doctors X-rayed my head and did not find anything.
A)X • ~F
B)X ~F
C)X ~F
D)X ~F
E)X F
A)X • ~F
B)X ~F
C)X ~F
D)X ~F
E)X F

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
43
Identify which of the following is a correct symbolization of the following statement. If you say it cannot be done, you should not interrupt the one doing it.
A)~S • ~I
B)~S ~I
C)~S ~I
D)~S ~I
E)S ~I
A)~S • ~I
B)~S ~I
C)~S ~I
D)~S ~I
E)S ~I

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
44
If both conjuncts of a conjunction are tautologies, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
45
Identify the main connective in the following statement. {[(P P) P] P} (P P)
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
46
In the truth table for the statement form ( p • q) p, the column of truth values underneath the main connective should be TTTT.Therefore, this statement form is a:
A)tautology
B)self-contradiction
C)contingency
D)equivalency
E)contradiction
A)tautology
B)self-contradiction
C)contingency
D)equivalency
E)contradiction

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
47
Identify the main connective in the following statement. [(G • O) (A ~M)] [(G • O) (A ~M)]
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
48
Identify the main connective in the following statement. (D • N) G
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
49
Identify which of the following is a correct symbolization of the following statement. If you argue with a fool, people might not know who is the fool.
A)A • ~K
B)A ~K
C)A ~K
D)A ~K
E)~A K
A)A • ~K
B)A ~K
C)A ~K
D)A ~K
E)~A K

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
50
Identify which of the following is a correct symbolization of the following statement. The Greeks won the battle but lost the war.
A)B • W
B)B W
C)B W
D)B W
E)B ~W
A)B • W
B)B W
C)B W
D)B W
E)B ~W

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
51
Identify the main connective in the following statement. {[(F R) ~(W • T)] • (N • P)} (L ~M)
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
52
Identify the main connective in the following statement. (N T) [(S M) • ~(H T)]
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
53
Identify the main connective in the following statement. L [(W L) ~(Y T)]
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
54
Identify the main connective in the following statement. [(N • D) (T M)] ~N
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
55
The negation of a self-contradiction is itself a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
56
Identify the main connective in the following statement. (D N) • (F Y)
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
57
Identify the main connective in the following statement. [(F L) (L I)] • (S T)
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
58
Identify which of the following is a correct symbolization of the following statement. If the shoe fits, then one has to wear it.
A)F • W
B)F W
C)F W
D)F W
E)F
A)F • W
B)F W
C)F W
D)F W
E)F

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
59
Identify the main connective in the following statement. (T ~E) (C • M)
A)•
B)
C)
D)
E)~
A)•
B)
C)
D)
E)~

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
60
Below is an incomplete truth table for the statement form [( p q) • p] q. The truth-value assignment underneath the main connective should be TTTT.Therefore, the statement form [( p q) • p] q is a:
A)tautology
B)self-contradiction
C)contingency
D)equivalency
E)contradiction
A)tautology
B)self-contradiction
C)contingency
D)equivalency
E)contradiction

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
61
If neither disjunct of a disjunction is a tautology, then the disjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
62
The negation of a tautology is itself a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
63
If both main components of a biconditional are tautologies, then the biconditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
64
If the antecedent of a conditional is a tautology, then the conditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
65
If at least one disjunct of a disjunction is a tautology, then the disjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
66
If the antecedent of a conditional is a self-contradiction, then the conditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
67
If at least one conjunct of a conjunction is a tautology, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
68
If only one conjunct of a conjunction is a tautology, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
69
If both conjuncts of a conjunction are self-contradictions, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
70
If only one conjunct of a conjunction is a self-contradiction, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
71
If both main components of a biconditional are self-contradictions, then the biconditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
72
If neither main component of a biconditional is a tautology, then the biconditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
73
If only one main component of a biconditional is a tautology, then the biconditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
74
In the truth table for the statement form ~(p p), the column of truth values underneath the main connective should be FF.Therefore, this statement form is a:
A)tautology
B)self-contradiction
C)contingency
D)equivalency
E)contradiction
A)tautology
B)self-contradiction
C)contingency
D)equivalency
E)contradiction

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
75
If the consequent of a conditional is a tautology, then the conditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
76
If only one disjunct of a disjunction is a tautology, then the disjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
77
If at least one conjunct of a conjunction is a self-contradiction, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
78
If both disjuncts of a disjunction are tautologies, then the disjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
79
If at least one main component of a biconditional is a tautology, then the biconditional itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck
80
If neither conjunct of a conjunction is a tautology, then the conjunction itself is a:
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given
A)tautology
B)self-contradiction
C)contingency
D)coherency
E)unable to determine from the information given

Unlock Deck
Unlock for access to all 223 flashcards in this deck.
Unlock Deck
k this deck


