Deck 8: Nonlinear Optimization Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/48
Play
Full screen (f)
Deck 8: Nonlinear Optimization Models
1
An investor can pick the mean-variance tradeoff that he or she is most comfortable with by looking at a graph of the
A)feasible region.
B)pooled components.
C)rolling horizon.
D)efficient frontier.
A)feasible region.
B)pooled components.
C)rolling horizon.
D)efficient frontier.
D
2
A feasible solution is a global optimum if there are no other feasible solutions with a better objective function value in the immediate neighborhood.
False
3
Which of the following is incorrect?
A)A global optimum is a local optimum in a nonlinear optimization problem.
B)A local maximum is a global maximum in a concave nonlinear optimization problem.
C)A global minimum is a local minimum in a convex nonlinear optimization problem.
D)A local optimum is a global optimum in a nonlinear optimization problem.
A)A global optimum is a local optimum in a nonlinear optimization problem.
B)A local maximum is a global maximum in a concave nonlinear optimization problem.
C)A global minimum is a local minimum in a convex nonlinear optimization problem.
D)A local optimum is a global optimum in a nonlinear optimization problem.
D
4
A function is quadratic if its nonlinear terms have a power of 4.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
5
In the Bass model for forecasting the adoption of a new product, the objective function
A)minimizes the sum of forecast errors.
B)minimizes the sum of squared forecast errors.
C)maximizes the number of adoptions.
D)maximizes the number of adoptions and imitations.
A)minimizes the sum of forecast errors.
B)minimizes the sum of squared forecast errors.
C)maximizes the number of adoptions.
D)maximizes the number of adoptions and imitations.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
6
Many linear programming algorithms such as the simplex method optimize by examining only the extreme points of the feasible region.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
7
Nonlinear programming algorithms are more complex than linear programming algorithms.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
8
If the coefficient of each squared term in a quadratic function is positive, the function is
A)concave.
B)convex.
C)elliptical.
D)sinusoidal.
A)concave.
B)convex.
C)elliptical.
D)sinusoidal.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
9
Nonlinear optimization problems can have only one local optimal solution.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
10
A feasible solution is a global optimum if there are no other feasible points with a better objective function value in the feasible region.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
11
When the number of blending components exceeds the number of storage facilities, the number of feasible solutions to the blending problem
A)is reduced.
B)is increased.
C)is unchanged.
D)is zero.
A)is reduced.
B)is increased.
C)is unchanged.
D)is zero.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following is not true regarding a concave function?
A)It is bowl-shaped down.
B)It is relatively easy to maximize.
C)It has multiple local maxima.
D)It has a single global maximum.
A)It is bowl-shaped down.
B)It is relatively easy to maximize.
C)It has multiple local maxima.
D)It has a single global maximum.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
13
The measure of risk most often associated with the Markowitz portfolio model is the
A)portfolio average return.
B)portfolio minimum return.
C)portfolio variance.
D)portfolio standard deviation.
A)portfolio average return.
B)portfolio minimum return.
C)portfolio variance.
D)portfolio standard deviation.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
14
A convex function is
A)bowl-shaped up.
B)bowl-shaped down.
C)elliptical in shape.
D)sinusoidal in shape.
A)bowl-shaped up.
B)bowl-shaped down.
C)elliptical in shape.
D)sinusoidal in shape.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
15
Components that share a storage facility are called
A)constrained components.
B)indexed components.
C)blended components.
D)pooled components.
A)constrained components.
B)indexed components.
C)blended components.
D)pooled components.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
16
For a typical nonlinear problem, duals price are relatively insensitive to small changes in right-hand side values.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
17
A nonlinear optimization problem is any optimization problem in which at least one term in the objective function or a constraint is nonlinear.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is not a parameter of the Bass model for forecasting adoption of a new product?
A)the coefficient of innovation
B)the coefficient of interaction
C)the coefficient of imitation
D)the estimated number of people to eventually adopt the new product
A)the coefficient of innovation
B)the coefficient of interaction
C)the coefficient of imitation
D)the estimated number of people to eventually adopt the new product

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
19
The interpretation of the dual price for nonlinear models is different than the interpretation of the dual price for linear models.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
20
The key idea behind constructing an index fund is to choose a portfolio of securities that
A)is a mix of growth-oriented and income-oriented stocks.
B)minimizes risk without sacrificing liquidity.
C)mimics the performance of a broad market index.
D)balances short-term and long-term investments.
A)is a mix of growth-oriented and income-oriented stocks.
B)minimizes risk without sacrificing liquidity.
C)mimics the performance of a broad market index.
D)balances short-term and long-term investments.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
21
When components (or ingredients) in a blending problem must be pooled, the number of feasible solutions is reduced.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
22
Explain how the local minimum, local maximum, local optimum, global minimum, global maximum, and global optimum relate to one another in nonlinear optimization problems.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
23
For a minimization problem, a point is a global minimum if there are no other feasible points with a smaller objective function value.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
24
Provide several examples of both nonlinear objective functions and nonlinear constraints.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
25
Investment manager Max Gaines has several clients who wish to own a mutual fund portfolio that matches, as a whole, the performance of the S&P 500 stock index. His task is to determine what proportion of the portfolio should be invested in each of the five mutual funds listed below so that the portfolio most closely mimics the performance of the S&P 500 index. Formulate the appropriate nonlinear program.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
26
Each point on the efficient frontier is the maximum possible risk, measured by portfolio variance, for the given return.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
27
The function f (X, Y) = X 2 + Y 2 has a single global minimum and is relatively easy to minimize.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
28
Any feasible solution to a blending problem with pooled components is feasible to the problem with no pooling.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
29
Because most nonlinear optimization codes will terminate with a local optimum, the solution returned by the codes will be the best solution.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
30
The Markowitz mean-variance portfolio model presented in the text is a convex optimization problem.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
31
Functions that are convex have a single local maximum that is also the global maximum.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
32
Explain how the parameters required for the Bass new-product adoption model can be estimated when no historical data are available for the new product.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
33
Discuss the essence of the pooling problem in terms of the circumstances, objective, and constraints.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
34
The problem of maximizing a concave quadratic function over a linear constraint set is relatively difficult to solve.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
35
Describe how the Markowitz portfolio model can be modified to account for upper and lower bounds being placed on the amount of an asset type invested in the portfolio.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
36
In the case of functions with multiple local optima, most nonlinear optimization software methods can get stuck and terminate at a local optimum.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
37
Financial planner Minnie Margin has a substantial number of clients who wish to own a mutual fund portfolio that matches, as a whole, the performance of the Russell 2000 index. Her task is to determine what proportion of the portfolio should be invested in each of the five mutual funds listed below so that the portfolio most closely mimics the performance of the Russell 2000 index. Formulate the appropriate nonlinear program.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
38
There are nonlinear applications in which there is a single local optimal solution that is also the global optimal solution.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
39
The value of the coefficient of imitation, q, in the Bass model for forecasting adoption of a new product cannot be negative.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
40
Any feasible solution to a blending problem without pooled components is feasible to the problem with pooled components.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
41
Financial planner Minnie Margin wishes to develop a mutual fund portfolio based on the Markowitz portfolio model. She needs to determine the proportion of the portfolio to invest in each of the five mutual funds listed below so that the variance of the portfolio is minimized subject to the constraint that the expected return of the portfolio be at least 5%. Formulate the appropriate nonlinear program. 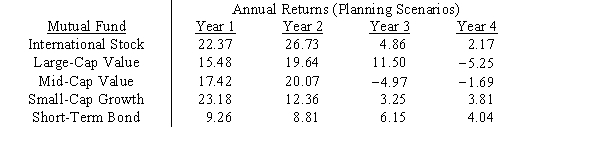
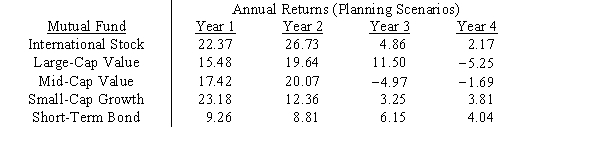

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
42
Skooter's Skateboards produces two models of skateboards, the FX and the ZX. Skateboard revenue (in $l,000s) for the firm is nonlinear and is stated as (number of FXs)(5-0.2 number of FXs) + (number of ZXs)(7 - 0.3 number of ZXs). Skooter's has 80 labor-hours available per week in its paint shop. Each FX requires 2 labor-hours to paint and each ZX requires 3 labor-hours. Formulate this nonlinear production planning problem to determine how many FX and ZX skateboards should be produced per week at Scooter's.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
43
Native Customs sells two popular styles of hand-sewn footwear: a sandal and a moccasin. The cost to make a pair of sandals is $18, and the cost to make a pair of moccasins is $24. The demand for these two items is sensitive to the price, and historical data indicate that the monthly demands are given by S = 400 -10P1 and M = 450 - 15P2 , where S = demand for sandals (in pairs), M = demand for moccasins (in pairs), P1 = price for a pair of sandals, and P2 = price for a pair of moccasins. To remain competitive, Native Customs must limit the price (per pair) to no more than $60 and $75 for its sandals and moccasins, respectively. Formulate this nonlinear programming problem to find the optimal production quantities and prices for sandals and moccasins that maximize total monthly profit.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
44
Cutting Edge Yard Care is a residential and commercial lawn service company that has been in business in the Atlanta metropolitan area for almost one year. Cutting Edge would like to use its Atlanta service subscription data below to develop a model for forecasting service subscriptions in other metropolitan areas where it might expand. The first step is to estimate values for p (coefficient of innovation) and q (coefficient of imitation). Formulate the appropriate nonlinear program. 


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
45
Investment manager Max Gaines wishes to develop a mutual fund portfolio based on the Markowitz portfolio model. He needs to determine the proportion of the portfolio to invest in each of the five mutual funds listed below so that the variance of the portfolio is minimized subject to the constraint that the expected return of the portfolio be at least 4%. Formulate the appropriate nonlinear program.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
46
Pacific-Gulf Oil Company is faced with the problem of refining three petroleum components into regular and premium gasoline in order to maximize profit. Components 1 and 2 are pooled in a single storage tank and component 3 has its own storage tank. Regular and premium gasolines are made from blending the pooled components and component 3. Prices per gallon for the two products and three components, as well as product specifications, are listed below. The maximum number of gallons available for each of the three components is 4000, 8000, and 8000, respectively. Formulate a nonlinear program to determine: 1) what percentages of component 1 and component 2 should be used in the pooled mixture, and 2) how to make regular and premium gasoline by blending the mixture of components 1 and 2 from the pooling tank with component 3.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
47
MegaSports, Inc. produces two high-priced metal baseball bats, the Slugger and the Launcher, that are made from special aluminum and steel alloys. The cost to produce a Slugger bat is $100, and the cost to produce a Launcher bat is $120. We can not assume that MegaSports will sell all the bats it can produce. As the selling price of each bat model -- Slugger and Launcher -- increases, the quantity demanded for each model goes down.
Assume that the demand, S, for Slugger bats is given by S = 640 - 4PS and the demand, L, for Launcher bats is given by L = 450 - 3PL where PS is the price of a Slugger bat and PL is the price of a Launcher bat. The profit contributions are PS S - 100S for Slugger bats and PL L - 120L for Launcher bats. Develop the total profit contribution function for this problem.
Assume that the demand, S, for Slugger bats is given by S = 640 - 4PS and the demand, L, for Launcher bats is given by L = 450 - 3PL where PS is the price of a Slugger bat and PL is the price of a Launcher bat. The profit contributions are PS S - 100S for Slugger bats and PL L - 120L for Launcher bats. Develop the total profit contribution function for this problem.

Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck
48
Shampooch is a mobile dog grooming service firm that has been quite successful developing a client base in the Dallas area. The firm plans to expand to other cities in Texas during the next few years. Shampooch would like to use its Dallas subscription data shown below to develop a model for forecasting service subscriptions in cities where it might expand. The first step is to estimate values for p (coefficient of innovation) and q (coefficient of imitation). Formulate the appropriate nonlinear program. 


Unlock Deck
Unlock for access to all 48 flashcards in this deck.
Unlock Deck
k this deck


