Deck 14: Multicriteria Decisions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/45
Play
Full screen (f)
Deck 14: Multicriteria Decisions
1
There can only be one goal at each priority level.
False
2
Goal programming with preemptive priorities never permits trade-offs between
A)goals with the same priority level and the same weights.
B)goals with different priority levels.
C)goals with the same priority level and different weights.
D)any goals.
A)goals with the same priority level and the same weights.
B)goals with different priority levels.
C)goals with the same priority level and different weights.
D)any goals.
B
3
Computing the consistency ratio for a criterion's pair-wise comparison matrix is the next step after
A)developing the criterion's pair-wise comparison matrix.
B)converting the criterion's pair-wise comparison matrix to a normalized matrix.
C)developing the criterion's priority vector.
D)developing the overall priority vector.
A)developing the criterion's pair-wise comparison matrix.
B)converting the criterion's pair-wise comparison matrix to a normalized matrix.
C)developing the criterion's priority vector.
D)developing the overall priority vector.
C
4
When using a linear programming approach to solving a goal programming problem, a linear program must be solved for each
A)goal.
B)pair of deviation variables.
C)priority level.
D)pair-wise comparison.
A)goal.
B)pair of deviation variables.
C)priority level.
D)pair-wise comparison.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
5
Inconsistency in the pair-wise judgments is indicated by a consistency ratio that is
A)less than zero
B)greater than 0.10
C)greater than 0.50
D)greater than 1.00
A)less than zero
B)greater than 0.10
C)greater than 0.50
D)greater than 1.00

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
6
A required step in the analytic hierarchy process is to determine
A)the goals to be satisfied.
B)the expected value of the criteria.
C)the relative importance of a set of features based on a criterion.
D)how many hierarchies to use.
A)the goals to be satisfied.
B)the expected value of the criteria.
C)the relative importance of a set of features based on a criterion.
D)how many hierarchies to use.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
7
Target values will never be met precisely in a goal programming problem.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
8
The steps of the scoring model include all of the following EXCEPT:
A)list the decision-making criteria and assign a weight to each.
B)develop a pair-wise comparison matrix for each criterion.
C)rate how well each decision alternative satisfies each criterion.
D)compute the total score for each decision alternative.
A)list the decision-making criteria and assign a weight to each.
B)develop a pair-wise comparison matrix for each criterion.
C)rate how well each decision alternative satisfies each criterion.
D)compute the total score for each decision alternative.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
9
Pair-wise comparisons are used to
A)compare criteria in terms of the overall goal.
B)compare choices on each criterion.
C)both a and b are true.
D)neither a nor b is true.
A)compare criteria in terms of the overall goal.
B)compare choices on each criterion.
C)both a and b are true.
D)neither a nor b is true.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
10
Goal equations consist of a function that defines goal achievement and deviation variables that measure the distance from the target.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
11
The variable d- measures
A)the amount over the target and is similar to a slack.
B)the amount under the target and is similar to a slack.
C)the amount over the target and is similar to a surplus.
D)the amount under the target and is similar to a surplus.
A)the amount over the target and is similar to a slack.
B)the amount under the target and is similar to a slack.
C)the amount over the target and is similar to a surplus.
D)the amount under the target and is similar to a surplus.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
12
A decision with more than one objective
A)cannot have an optimal solution.
B)requires the decision maker to place the objectives in some order of importance.
C)depends on the probability of satisfying each objective.
D)should be decomposed into a separate model for each objective.
A)cannot have an optimal solution.
B)requires the decision maker to place the objectives in some order of importance.
C)depends on the probability of satisfying each objective.
D)should be decomposed into a separate model for each objective.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
13
The overall priorities for decision alternatives
A)are the sum of the products of the criterion priority times the priority of the decision alternative with respect to that criterion.
B)sum to 1.
C)indicate what choice is preferred, but do not force that choice to be made.
D)each of the above is true.
A)are the sum of the products of the criterion priority times the priority of the decision alternative with respect to that criterion.
B)sum to 1.
C)indicate what choice is preferred, but do not force that choice to be made.
D)each of the above is true.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
14
To solve a goal programming problem with preemptive priorities, successive linear programming programs, with an adjustment to the objective function and an additional constraint, must be solved.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
15
The constraint 5x1 + 3x2 150 is modified to become a goal equation, and priority one is to avoid overutilization. Which of the following is appropriate?
A)Min P1d1- ; 5x1 + 3x2 + d1--d1+ = 150
B)Min P1d1+ ; 5x1 + 3x2 + d1- -d1+ = 150
C)Min P1d1+ ; 5x1 + 3x2 + d1+ = 150
D)Min P1d1+ ; 5x1 + 3x2 -d1+ = 150
A)Min P1d1- ; 5x1 + 3x2 + d1--d1+ = 150
B)Min P1d1+ ; 5x1 + 3x2 + d1- -d1+ = 150
C)Min P1d1+ ; 5x1 + 3x2 + d1+ = 150
D)Min P1d1+ ; 5x1 + 3x2 -d1+ = 150

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
16
Preemptive priorities in goal programming
A)show the target values for the problem.
B)prevent sacrifice of a goal to satisfy a lower level one.
C)force the problem to be a standard linear program.
D)limit deviations to d- only.
A)show the target values for the problem.
B)prevent sacrifice of a goal to satisfy a lower level one.
C)force the problem to be a standard linear program.
D)limit deviations to d- only.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
17
Deviation variables that occur in the objective function indicate
A)the targets.
B)the priorities.
C)only the areas that are of concern.
D)the difference between all actual and target values.
A)the targets.
B)the priorities.
C)only the areas that are of concern.
D)the difference between all actual and target values.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
18
Variables that indicate the distance a target is from the level achieved are called
A)goal variables.
B)target variables.
C)deviation variables.
D)preemptive variables.
A)goal variables.
B)target variables.
C)deviation variables.
D)preemptive variables.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
19
The goal programming problem with the objective function min P1(d1+) +P2(d2-) is initially solved by the computer and the objective function value is 0. What constraint should be added for the second problem?
A)d1+ = 0
B)d1+ + d2- = 0
C)-d1+ + d2- = 0
D)d1+ 0
A)d1+ = 0
B)d1+ + d2- = 0
C)-d1+ + d2- = 0
D)d1+ 0

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
20
Objectives in multicriteria problems seldom conflict.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
21
A problem involving only one priority level is not considered a goal programming problem.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
22
Explain the difference between hard and soft constraints in a goal programming problem.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
23
Explain why goal programming could be a good approach to use after a linear programming problem is found to be infeasible.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
24
The goal programming approach can be used when an analyst is confronted with an infeasible solution to an ordinary linear program.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
25
How can you be sure your rankings in AHP are consistent?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
26
The goal programming problem below was solved with the Management Scientist.
Min
P1(d1-) + P2(d2+) + P3(d3-)
s.t.
72x1 + 38x2 + 23x3 - 20,000
.72x1 -.76x2 - .23x3 + d1- - d1+ = 0
x3 + d2- - d2+ = 150
38x2 + d3- -d3+ = 2000
x1, x2, x3, d1-, d 1+, d2-, d2+, d3-, d3+ 0
Partial output from three successive linear programming problems is given. For each problem, give the original objective function expression and its value, and list any constraints needed beyond those that were in the original problem.
Min
P1(d1-) + P2(d2+) + P3(d3-)
s.t.
72x1 + 38x2 + 23x3 - 20,000
.72x1 -.76x2 - .23x3 + d1- - d1+ = 0
x3 + d2- - d2+ = 150
38x2 + d3- -d3+ = 2000
x1, x2, x3, d1-, d 1+, d2-, d2+, d3-, d3+ 0
Partial output from three successive linear programming problems is given. For each problem, give the original objective function expression and its value, and list any constraints needed beyond those that were in the original problem.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
27
The Lofton Company has developed the following linear programming problem  but finds it is infeasible. In revision, Lofton drops the original objective and establishes the three goals
but finds it is infeasible. In revision, Lofton drops the original objective and establishes the three goals
Goal 1:
Don't exceed 10 in constraint 1.
Goal 2:
Don't fall short of 36 in constraint 3.
Goal 3:
Don't exceed 24 in constraint 2.
Give the goal programming model and solve it graphically.
 but finds it is infeasible. In revision, Lofton drops the original objective and establishes the three goals
but finds it is infeasible. In revision, Lofton drops the original objective and establishes the three goalsGoal 1:
Don't exceed 10 in constraint 1.
Goal 2:
Don't fall short of 36 in constraint 3.
Goal 3:
Don't exceed 24 in constraint 2.
Give the goal programming model and solve it graphically.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
28
If airline A is moderately preferred to airline B, at a value of 3, then airline B is compared to airline A at a value of -3.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
29
One limitation of a scoring model is that it uses arbitrary weights that do not necessarily reflect the preferences of the individual decision maker.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
30
As treasurer of the school PTA, you chair the committee to decide how the $20,000 raised by candy sales will be spent. Four kinds of projects have been proposed, and facts on each are shown below. Develop a goal programming model that would represent these goals and priorities.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
31
Why are multicriteria problems of special interest to quantitative analysts?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
32
An ATM is to be located in a campus union building so that it minimizes the distance from the food court, the gift shop, and the theater. They are located at coordinates (2,2), (0,6) and (8,0). Develop a goal programming model to use to locate the best place for the ATM.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the following problem graphically: 


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
34
For a scoring model, the decision maker evaluates each decision alternative using equally weighted criteria.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
35
A consistency ratio greater than 0.10 indicates inconsistency in the pair-wise comparisons.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
36
If a problem has multiple goals at different priority levels, then usually they can all be achieved.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
37
The priority matrix shows the priority for each item on each criterion.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
38
Should the decision maker always accept the alternatives with the highest AHP rating? Explain.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
39
An item's priority reveals how it compares to its competitors on a specific criterion.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
40
Calculating the priority of each criterion in terms of its contribution to the overall goal is known as developing the hierarchy.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
41
A consumer group is using AHP to compare four used car models. Part of the pair-wise comparison matrix for "repair frequency" is shown below.
a.Complete the matrix.
b.Does it seem to be consistent?
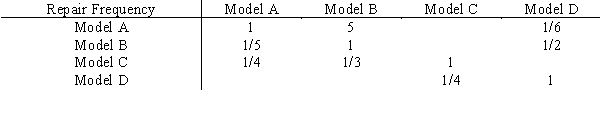
a.Complete the matrix.
b.Does it seem to be consistent?


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
42
Rosie's Ribs is in need of an office management software package. After considerable research, Rosie has narrowed her choice to one of three packages: N-able, VersaSuite, and SoftTrack. She has determined her decision-making criteria, assigned a weight to each criterion, and rated how well each alternative satisfies each criterion. 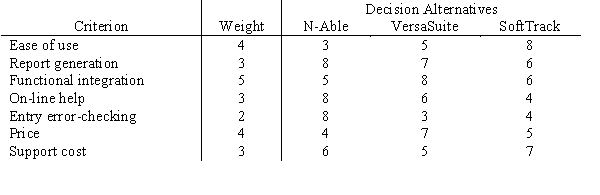 Using a scoring model, determine the recommended software package for Rosie's.
Using a scoring model, determine the recommended software package for Rosie's.
 Using a scoring model, determine the recommended software package for Rosie's.
Using a scoring model, determine the recommended software package for Rosie's.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
43
Like many high school seniors, Anne has several universities to consider when making her final college choice. To assist in her decision, she has decided to use AHP to develop a ranking for school R, school P, and school M. The schools will be evaluated on five criteria, and Anne's pair-wise comparison matrix for the criteria is shown below. 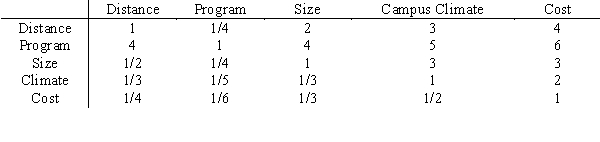 The universities' pair-wise comparisons on the criteria are shown below.
The universities' pair-wise comparisons on the criteria are shown below. 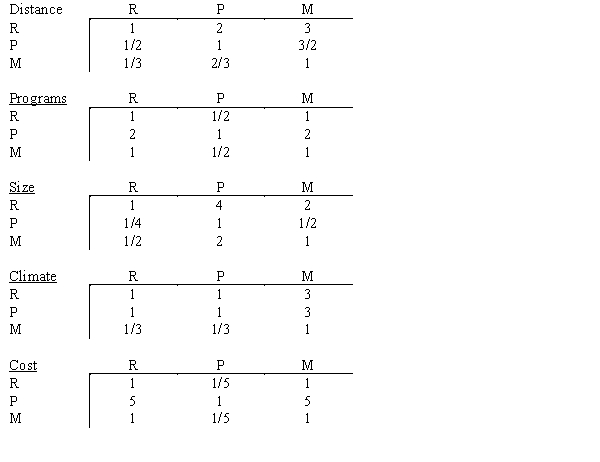
a.What is the overall ranking of the five criteria?
b.What is the overall ranking of the three universities?
 The universities' pair-wise comparisons on the criteria are shown below.
The universities' pair-wise comparisons on the criteria are shown below. 
a.What is the overall ranking of the five criteria?
b.What is the overall ranking of the three universities?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
44
In an AHP problem, the priorities for three criteria are  The priority matrix is
The priority matrix is  Compute the overall priority for each choice.
Compute the overall priority for each choice.
 The priority matrix is
The priority matrix is  Compute the overall priority for each choice.
Compute the overall priority for each choice.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
45
A computer company looking for a new location for a plant has determined three criteria to use to rate cities. Pair-wise comparisons are given.  Determine priorities for the three relative to the overall location goal.
Determine priorities for the three relative to the overall location goal.
 Determine priorities for the three relative to the overall location goal.
Determine priorities for the three relative to the overall location goal.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck


