Deck 21: Dynamic Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/30
Play
Full screen (f)
Deck 21: Dynamic Programming
1
Dynamic programming requires that its subproblems be independent of one another.
False
2
State variables are a function of a state variable and a decision.
True
3
The solution of stage k of a dynamic programming problem is dependent upon the solution of stage k-1.
True
4
The knapsack problem is to determine how many units of each item to place in the knapsack to:
A)minimize total value.
B)maximize total value.
C)minimize the number of items in the knapsack.
D)maximize the number of items in the knapsack.
A)minimize total value.
B)maximize total value.
C)minimize the number of items in the knapsack.
D)maximize the number of items in the knapsack.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
5
Stage transformation functions
A)are linear.
B)calculate the return.
C)determine the output of the stage.
D)All of the alternatives are true.
A)are linear.
B)calculate the return.
C)determine the output of the stage.
D)All of the alternatives are true.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
6
The stage transformation function
A)transforms the input into the output.
B)transforms a stage into a state.
C)is a different function for each stage.
D)None of the alternatives is true.
A)transforms the input into the output.
B)transforms a stage into a state.
C)is a different function for each stage.
D)None of the alternatives is true.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
7
Solutions in dynamic programming
A)are not optimal.
B)are unique.
C)represent each stage.
D)All of the alternatives are true.
A)are not optimal.
B)are unique.
C)represent each stage.
D)All of the alternatives are true.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
8
Dynamic programming, when used for the shortest route problem, requires complete enumeration of paths from the beginning to ending node.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
9
Stages of a dynamic programming solution procedure
A)represent parts of a large mathematical model.
B)often represent a sequence of decisions made over time.
C)are usually not independent of each other.
D)All of the alternatives are true.
A)represent parts of a large mathematical model.
B)often represent a sequence of decisions made over time.
C)are usually not independent of each other.
D)All of the alternatives are true.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
10
Dynamic programming is a general approach rather than a specific technique.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
11
In solving a shortest route problem using dynamic programming the stages represent how many arcs you are from the terminal node.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
12
If x3 = t4 (x4,d4) = x4 -2d4 and r4(x4,d4) = 16d4 the state variable is
A)t
B)x
C)r
D)d
A)t
B)x
C)r
D)d

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
13
The output of stage k is the input for stage k-1.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
14
If x3 = t4(x4,d4) = x4 - 2d4 and r4(x4,d4) = 16d4, the subscripts refer to
A)state.
B)stage.
C)transformation.
D)return.
A)state.
B)stage.
C)transformation.
D)return.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
15
The return function for a shortest route problem refers to two directional arcs between nodes.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
16
If x3 = t4(x4,d4) = x4 -2d4 and r4(x4,d4) = 16d4, the stage transformation function is
A)t
B)x
C)r
D)d
A)t
B)x
C)r
D)d

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
17
State variables in a shortest route problem represent
A)decisions.
B)locations in the network.
C)the minimum distance between nodes.
D)None of the alternatives is true.
A)decisions.
B)locations in the network.
C)the minimum distance between nodes.
D)None of the alternatives is true.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
18
A return function is a value such as profit or loss associated with making decision dn at:
A)stage n for specific value of output variable xn.
B)stage n for a specific value of input variable xn.
C)stage n for a specific value of stage m.
D)input n for a specific value of output variable xn.
A)stage n for specific value of output variable xn.
B)stage n for a specific value of input variable xn.
C)stage n for a specific value of stage m.
D)input n for a specific value of output variable xn.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
19
Dynamic programming must only involve a finite number of decision alternatives and a finite number of stages.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
20
Dynamic programming is a general approach with stage decision problems differing substantially from application to application.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
21
What is the Principle of Optimality, and what is its relationship to Dynamic Programming?

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
22
A driver wants to make a trip from city 1 to city 7. The road mileage between cities is given below. Find the shortest route. 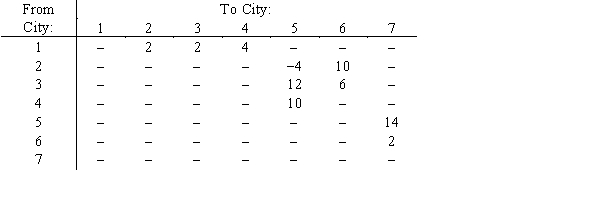


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following integer linear program
Max
5x1 + 7x2 + 9x3
s.t.
2x1 + 3x2 + 4x3 8
x1 3
x2 2
x1, x2, x3 0, integer
a.Set up the network that represents the dynamic programming formulation.
b.Solve the problem using dynamic programming.
Max
5x1 + 7x2 + 9x3
s.t.
2x1 + 3x2 + 4x3 8
x1 3
x2 2
x1, x2, x3 0, integer
a.Set up the network that represents the dynamic programming formulation.
b.Solve the problem using dynamic programming.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
24
A stage in a dynamic programming problem is defined when 2 variables and 2 functions related to that stage are defined. Identify and define the 2 variables and 2 functions and illustrate them with an example of your choice.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
25
The owner of a small construction firm is excavating at three sites. He wishes to assign his 5 additional trucks in such a way as to minimize his total costs. Each site can use 0 to 3 additional trucks; no site can use more than 3 trucks efficiently. The following site total costs are known. 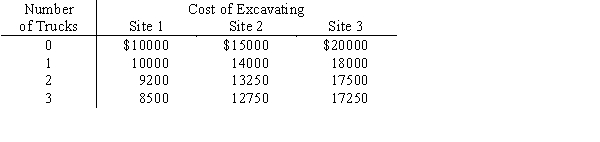
a.Use dynamic programming to find the assignment of the additional trucks that minimizes total cost.
b.If the owner had only 4 trucks to assign, what would be the optimal assignment and total cost?

a.Use dynamic programming to find the assignment of the additional trucks that minimizes total cost.
b.If the owner had only 4 trucks to assign, what would be the optimal assignment and total cost?

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
26
A cargo company has a set of delivery patterns for its goods from its locations at city1 to a series of cities 2,3,4,5, and 6. The delivery times between cities are given I hours below. Find the shortest route. 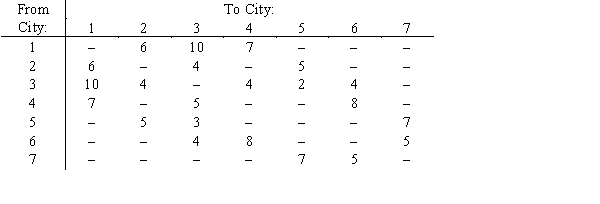


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
27
We have a number of types of items to be shipped as cargo. The total available weight in the truck is ten tons. We wish to determine the number of units of items to be shipped to maximize profit. 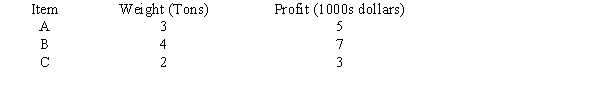
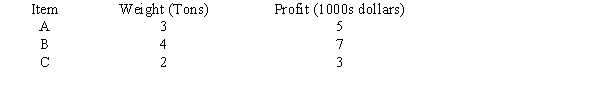

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
28
Audio Disks will be opening outlets in the greater Phoenix area. The estimated sales at each store are dependent not only on the store location, but on the number of sales personnel, as presented in the table below ($000/year). Each store requires at least 2 sales people, and a pool of 9 salespeople is available. 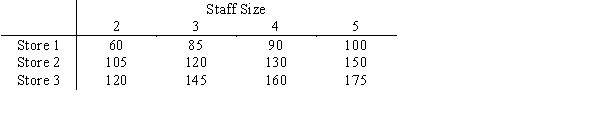
a.What would the states be in the dynamic programming formulation?
b.Draw the network that represents the dynamic programming formulation.
c.Given the above network, solve the sales personnel allocation problem by finding the longest path.

a.What would the states be in the dynamic programming formulation?
b.Draw the network that represents the dynamic programming formulation.
c.Given the above network, solve the sales personnel allocation problem by finding the longest path.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
29
Define the following terms as they relate to dynamic programming.
a.Stage.
b.State variable.
c.Stage transformation function.
a.Stage.
b.State variable.
c.Stage transformation function.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
30
Find the shortest path through the following network using dynamic programming. 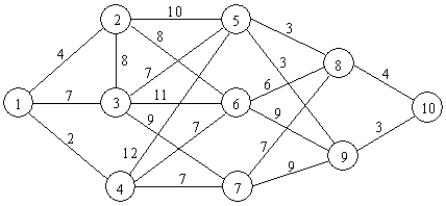


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck


