Deck 15: Multiple Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/103
Play
Full screen (f)
Deck 15: Multiple Regression
1
A variable that takes on the values of 0 or 1 and is used to incorporate the effect of categorical independent variables in a regression model is called
A) an interaction.
B) a constant variable.
C) a dummy variable.
D) a logit variable.
A) an interaction.
B) a constant variable.
C) a dummy variable.
D) a logit variable.
a dummy variable.
2
The adjusted multiple coefficient of determination is adjusted for the
A) number of dependent variables.
B) number of independent variables.
C) number of equations.
D) sample size.
A) number of dependent variables.
B) number of independent variables.
C) number of equations.
D) sample size.
number of independent variables.
3
In a multiple regression model, the variance of the error term ε is assumed to be
A) the same for all values of the dependent variable.
B) zero.
C) the same for all values of the independent variable.
D) one.
A) the same for all values of the dependent variable.
B) zero.
C) the same for all values of the independent variable.
D) one.
the same for all values of the independent variable.
4
In a multiple regression model, the error term ε is assumed to be a random variable with a mean of
A) zero.
B) -1.
C) 1.
D) any value.
A) zero.
B) -1.
C) 1.
D) any value.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
5
A multiple regression model has
A) only one independent variable.
B) more than one dependent variable.
C) more than one independent variable.
D) at least two dependent variables.
A) only one independent variable.
B) more than one dependent variable.
C) more than one independent variable.
D) at least two dependent variables.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
6
In a multiple regression model, the error term ε is assumed to
A) have a mean of 1.
B) have a variance of zero.
C) have no distribution.
D) be normally distributed.
A) have a mean of 1.
B) have a variance of zero.
C) have no distribution.
D) be normally distributed.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
7
In regression analysis, the response variable is the
A) independent variable.
B) dependent variable.
C) slope of the regression function.
D) intercept.
A) independent variable.
B) dependent variable.
C) slope of the regression function.
D) intercept.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
8
A measure of identifying the effect of an unusual x value on the regression results is called
A) Cook's D.
B) Leverage.
C) odd ratio.
D) unusual regression.
A) Cook's D.
B) Leverage.
C) odd ratio.
D) unusual regression.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
9
In multiple regression analysis, the correlation among the independent variables is termed
A) adjusted correlation.
B) linearity.
C) multicollinearity.
D) adjusted coefficient of determination.
A) adjusted correlation.
B) linearity.
C) multicollinearity.
D) adjusted coefficient of determination.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
10
The equation which has the form of E(y) = 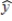 = b0 + b1x1 + b2x2 + ...+ bpxp is a(n)
= b0 + b1x1 + b2x2 + ...+ bpxp is a(n)
A) estimated multiple nonlinear regression equation.
B) multiple nonlinear regression model.
C) estimated multiple regression equation.
D) multiple regression equation.
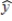 = b0 + b1x1 + b2x2 + ...+ bpxp is a(n)
= b0 + b1x1 + b2x2 + ...+ bpxp is a(n)A) estimated multiple nonlinear regression equation.
B) multiple nonlinear regression model.
C) estimated multiple regression equation.
D) multiple regression equation.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
11
In order to test for the significance of a regression model involving 3 independent variables and 47 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are
A) 47 and 3.
B) 3 and 47.
C) 2 and 43.
D) 3 and 43.
A) 47 and 3.
B) 3 and 47.
C) 2 and 43.
D) 3 and 43.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
12
The mathematical equation that explains how the dependent variable y is related to several independent variables x1, x2, …, xp and the error term ε is a(n)
A) simple nonlinear regression model.
B) multiple regression model.
C) estimated multiple regression equation.
D) multiple regression equation.
A) simple nonlinear regression model.
B) multiple regression model.
C) estimated multiple regression equation.
D) multiple regression equation.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
13
A measure of goodness of fit for the estimated regression equation is the
A) multiple coefficient of determination.
B) multicollinearity.
C) mean square due to regression.
D) studentized residual.
A) multiple coefficient of determination.
B) multicollinearity.
C) mean square due to regression.
D) studentized residual.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
14
A term used to describe the case when the independent variables in a multiple regression model are correlated is
A) regression.
B) correlation.
C) multicollinearity.
D) leverage.
A) regression.
B) correlation.
C) multicollinearity.
D) leverage.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
15
In multiple regression analysis,
A) there can be any number of dependent variables, but only one independent variable.
B) the adjusted coefficient of determination can never be negative.
C) the multiple coefficient of determination must be larger than 1.
D) there can be several independent variables, but only one dependent variable.
A) there can be any number of dependent variables, but only one independent variable.
B) the adjusted coefficient of determination can never be negative.
C) the multiple coefficient of determination must be larger than 1.
D) there can be several independent variables, but only one dependent variable.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
16
The mathematical equation which has the form of E(y) = β0 + β1x1 + β2x2 + ...+ βpxp relating the expected value of the dependent variable to the value of the independent variables is a(n)
A) estimated multiple nonlinear regression equation.
B) multiple nonlinear regression model.
C) estimated multiple regression equation.
D) multiple regression equation.
A) estimated multiple nonlinear regression equation.
B) multiple nonlinear regression model.
C) estimated multiple regression equation.
D) multiple regression equation.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
17
A regression model in which more than one independent variable is used to predict the dependent variable is called
A) a simple linear regression model.
B) a multiple regression model.
C) an independent model.
D) an adjusted prediction model.
A) a simple linear regression model.
B) a multiple regression model.
C) an independent model.
D) an adjusted prediction model.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
18
The numerical value of the coefficient of determination.
A) is always larger than the coefficient of correlation.
B) is always smaller than the coefficient of correlation.
C) is negative if the coefficient of correlation is negative.
D) can be larger or smaller than the coefficient of correlation.
A) is always larger than the coefficient of correlation.
B) is always smaller than the coefficient of correlation.
C) is negative if the coefficient of correlation is negative.
D) can be larger or smaller than the coefficient of correlation.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
19
In regression analysis, an outlier is an observation whose
A) mean is larger than the standard deviation.
B) residual is zero.
C) mean is zero.
D) residual is much larger than the rest of the residual values.
A) mean is larger than the standard deviation.
B) residual is zero.
C) mean is zero.
D) residual is much larger than the rest of the residual values.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
20
In a multiple regression model, the values of the error term ε are assumed to be
A) zero.
B) dependent on each other.
C) independent of each other.
D) always negative.
A) zero.
B) dependent on each other.
C) independent of each other.
D) always negative.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
21
In a multiple regression analysis involving 15 independent variables and 200 observations, SST = 800 and SSE = 240.The multiple coefficient of determination is
A) .300.
B) .192.
C) .500.
D) .700.
A) .300.
B) .192.
C) .500.
D) .700.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
22
The multiple coefficient of determination is
A) MSR/MST.
B) MSR/MSE.
C) SSR/SST.
D) SSE/SSR.
A) MSR/MST.
B) MSR/MSE.
C) SSR/SST.
D) SSE/SSR.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
23
A regression model involved 5 independent variables and 136 observations.The critical value of t for testing the significance of each of the independent variable's coefficients will have
A) 121 degrees of freedom.
B) 135 degrees of freedom.
C) 130 degrees of freedom.
D) 4 degrees of freedom.
A) 121 degrees of freedom.
B) 135 degrees of freedom.
C) 130 degrees of freedom.
D) 4 degrees of freedom.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
24
In a multiple regression analysis involving 10 independent variables and 81 observations, SST = 100 and SSE = 40.The multiple coefficient of determination is
A) .241.
B) .11.
C) .40.
D) .60.
A) .241.
B) .11.
C) .40.
D) .60.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
25
The correct relationship between SST, SSR, and SSE is given by
A) SSR = SST + SSE.
B) SSR = SST - SSE.
C) SSE = SSR + SST.
D) n(SST) = p(SSR) + (n - p)(SSE).
A) SSR = SST + SSE.
B) SSR = SST - SSE.
C) SSE = SSR + SST.
D) n(SST) = p(SSR) + (n - p)(SSE).

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
26
In logistic regression,
A) there can only be two independent variables.
B) there are two dependent variables.
C) the dependent variable only assumes two discrete values.
D) the dependent variable only assumes two continuous values.
A) there can only be two independent variables.
B) there are two dependent variables.
C) the dependent variable only assumes two discrete values.
D) the dependent variable only assumes two continuous values.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
27
A regression model involved 20 independent variables and 200 observations.The critical value of t for testing the significance of each of the independent variable's coefficients will have
A) 18 degrees of freedom.
B) 200 degrees of freedom.
C) 199 degrees of freedom.
D) 179 degrees of freedom.
A) 18 degrees of freedom.
B) 200 degrees of freedom.
C) 199 degrees of freedom.
D) 179 degrees of freedom.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
28
In a multiple regression analysis involving 10 independent variables and 165 observations, SSR = 878 and SSE = 122.The multiple coefficient of determination is
A) .1389.
B) .122.
C) .878.
D) .7317.
A) .1389.
B) .122.
C) .878.
D) .7317.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
29
In order to test for the significance of a regression model involving 14 independent variables and 260 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are
A) 14 and 260.
B) 260 and 14.
C) 13 and 245.
D) 14 and 245.
A) 14 and 260.
B) 260 and 14.
C) 13 and 245.
D) 14 and 245.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
30
For a multiple regression model, SSR = 600 and SSE = 200.The multiple coefficient of determination is
A) .333.
B) .275.
C) .30.
D) .75.
A) .333.
B) .275.
C) .30.
D) .75.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
31
In a multiple regression analysis, SSR = 1000 and SSE = 200.The F statistic for this model is
A) 5.
B) 1200.
C) 800.
D) Not enough information is provided to answer this question.
A) 5.
B) 1200.
C) 800.
D) Not enough information is provided to answer this question.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
32
For a multiple regression model, SST = 200 and SSE = 60.The multiple coefficient of determination is
A) .25.
B) .30.
C) .80.
D) .70.
A) .25.
B) .30.
C) .80.
D) .70.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
33
In multiple regression analysis, a variable that cannot be measured in numerical terms is called a
A) nonmeasurable random variable.
B) constant variable.
C) dependent variable.
D) categorical independent variable.
A) nonmeasurable random variable.
B) constant variable.
C) dependent variable.
D) categorical independent variable.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
34
In a situation where the dependent variable can assume only one of the two possible discrete values,
A) we must use multiple regression.
B) there can only be two independent variables.
C) logistic regression should be applied.
D) all the independent variables must have values of either zero or one.
A) we must use multiple regression.
B) there can only be two independent variables.
C) logistic regression should be applied.
D) all the independent variables must have values of either zero or one.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
35
In order to test for the significance of a regression model involving 9 independent variables and 121 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are
A) 9 and 121.
B) 7 and 120.
C) 9 and 111.
D) 7 and 111.
A) 9 and 121.
B) 7 and 120.
C) 9 and 111.
D) 7 and 111.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
36
A multiple regression model has the estimated form 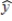 = 5 + 6x + 7w
= 5 + 6x + 7w
As x increases by 1 unit (holding x constant), y is expected to
A) increase by 11 units.
B) decrease by 11 units.
C) increase by 7 units.
D) decrease by 7 units.
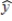 = 5 + 6x + 7w
= 5 + 6x + 7w
As x increases by 1 unit (holding x constant), y is expected to
A) increase by 11 units.
B) decrease by 11 units.
C) increase by 7 units.
D) decrease by 7 units.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
37
A regression analysis involved 8 independent variables and 100 observations.The critical value of t for testing the significance of each of the independent variable's coefficients will have
A) 9 degrees of freedom.
B) 97 degrees of freedom.
C) 91 degrees of freedom.
D) 7 degrees of freedom.
A) 9 degrees of freedom.
B) 97 degrees of freedom.
C) 91 degrees of freedom.
D) 7 degrees of freedom.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
38
In a regression model involving more than one independent variable, which of the following tests must be used in order to determine if the relationship between the dependent variable and the set of independent variables is significant?
A) t test
B) F test
C) Either a t test or a chi-square test can be used.
D) chi-square test
A) t test
B) F test
C) Either a t test or a chi-square test can be used.
D) chi-square test

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
39
A multiple regression model has the estimated form 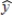 = 7 + 3x1 + 9x2
= 7 + 3x1 + 9x2
As x1 increases by 1 unit (holding x2 constant), y is expected to
A) increase by 9 units.
B) decrease by 9 units.
C) increase by 3 units.
D) decrease by 3 units.
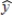 = 7 + 3x1 + 9x2
= 7 + 3x1 + 9x2
As x1 increases by 1 unit (holding x2 constant), y is expected to
A) increase by 9 units.
B) decrease by 9 units.
C) increase by 3 units.
D) decrease by 3 units.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
40
The ratio of MSR to MSE yields
A) SST.
B) the F statistic.
C) SSR.
D) the chi-square statistic.
A) SST.
B) the F statistic.
C) SSR.
D) the chi-square statistic.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
41
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 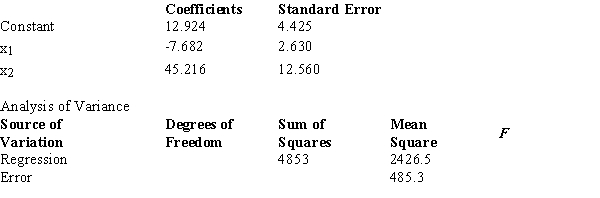 The interpretation of the coefficient of x1 is that
The interpretation of the coefficient of x1 is that
A) a one unit change in x1 will lead to a 7.682 unit decrease in y.
B) a one unit increase in x1 will lead to a 7.682 unit decrease in y when all other variables are held constant.
C) a one unit increase in x1 will lead to a 7.682 unit decrease in x2 when all other variables are held constant.
D) The unit of measurement for y is required to interpret the coefficient.
 The interpretation of the coefficient of x1 is that
The interpretation of the coefficient of x1 is thatA) a one unit change in x1 will lead to a 7.682 unit decrease in y.
B) a one unit increase in x1 will lead to a 7.682 unit decrease in y when all other variables are held constant.
C) a one unit increase in x1 will lead to a 7.682 unit decrease in x2 when all other variables are held constant.
D) The unit of measurement for y is required to interpret the coefficient.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
42
In a multiple regression model involving 44 observations, the following estimated regression equation was obtained. 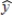 = 50+ 13x1 + 40x2 + 68x3
= 50+ 13x1 + 40x2 + 68x3
For this model, SSR = 600 and SSE = 300.MSR for this model is
A) 200.
B) 10.
C) 1000.
D) 43.
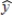 = 50+ 13x1 + 40x2 + 68x3
= 50+ 13x1 + 40x2 + 68x3
For this model, SSR = 600 and SSE = 300.MSR for this model is
A) 200.
B) 10.
C) 1000.
D) 43.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
43
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 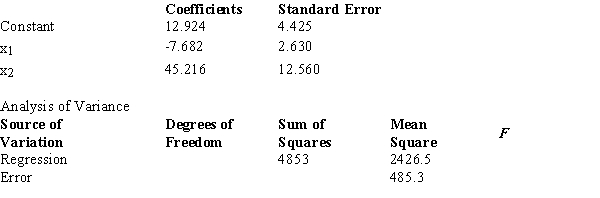 The degrees of freedom for the sum of squares explained by the regression (SSR) are
The degrees of freedom for the sum of squares explained by the regression (SSR) are
A) 2.
B) 3.
C) 13.
D) 15.
 The degrees of freedom for the sum of squares explained by the regression (SSR) are
The degrees of freedom for the sum of squares explained by the regression (SSR) areA) 2.
B) 3.
C) 13.
D) 15.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
44
In order to test for the significance of a regression model involving 5 independent variables and 36 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are
A) 4 and 36.
B) 3 and 35.
C) 5 and 30.
D) 5 and 31.
A) 4 and 36.
B) 3 and 35.
C) 5 and 30.
D) 5 and 31.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
45
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 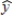 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.To test for the significance of the model, the p-value is
A) less than .01.
B) between .01 and .025.
C) between .025 and .05.
D) greater than .10.
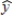 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.To test for the significance of the model, the p-value is
A) less than .01.
B) between .01 and .025.
C) between .025 and .05.
D) greater than .10.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
46
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 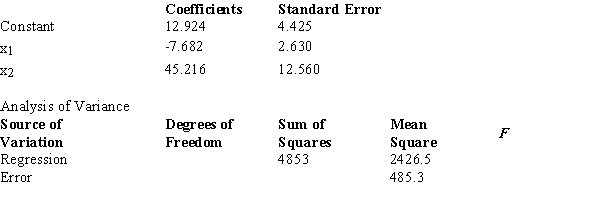 We want to test whether the parameter β1 is significant.The test statistic equals
We want to test whether the parameter β1 is significant.The test statistic equals
A) -2.9.
B) 2.9.
C) 3.6.
D) -5.0.
 We want to test whether the parameter β1 is significant.The test statistic equals
We want to test whether the parameter β1 is significant.The test statistic equalsA) -2.9.
B) 2.9.
C) 3.6.
D) -5.0.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
47
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function:  = 7 - 4x1 + 5x2
= 7 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.The adjusted multiple coefficient of determination for this problem is
A) .70.
B) .8367.
C) .6647.
D) .3353.
 = 7 - 4x1 + 5x2
= 7 - 4x1 + 5x2For this model, SSR = 3500, SSE = 1500, and the sample size is 20.The adjusted multiple coefficient of determination for this problem is
A) .70.
B) .8367.
C) .6647.
D) .3353.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
48
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function:  = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.The coefficient of x2 indicates that if television advertisement is increased by $1 (holding the unit price constant), sales are expected to
A) increase by $5.
B) increase by $20,000.
C) increase by $5000.
D) decrease by $4000.
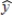 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.The coefficient of x2 indicates that if television advertisement is increased by $1 (holding the unit price constant), sales are expected to
A) increase by $5.
B) increase by $20,000.
C) increase by $5000.
D) decrease by $4000.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
49
In a multiple regression model involving 50 observations, the following estimated regression equation was obtained: 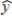 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.The multiple coefficient of determination for the above model is
A) .934.
B) .875.
C) .125.
D) .144.
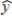 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.The multiple coefficient of determination for the above model is
A) .934.
B) .875.
C) .125.
D) .144.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
50
In a multiple regression model involving 50 observations, the following estimated regression equation was obtained: 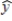 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.At the 5% level,
A) there is no evidence that the model is significant.
B) it can be concluded that the model is significant.
C) the conclusion is that the slope of x1 is significant.
D) there is evidence that the slope of x2 is significant.
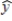 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.At the 5% level,
A) there is no evidence that the model is significant.
B) it can be concluded that the model is significant.
C) the conclusion is that the slope of x1 is significant.
D) there is evidence that the slope of x2 is significant.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
51
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 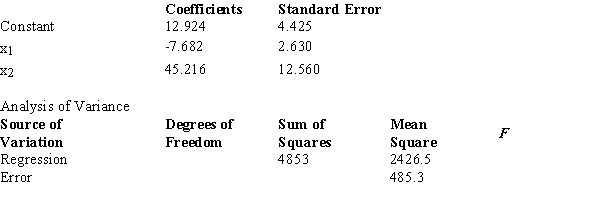 Carry out the test of significance for the parameter β1 at the 1% level.The null hypothesis should
Carry out the test of significance for the parameter β1 at the 1% level.The null hypothesis should
A) be rejected.
B) not be rejected.
C) be revised to test using F statistic.
D) be tested for β₃ instead.
 Carry out the test of significance for the parameter β1 at the 1% level.The null hypothesis should
Carry out the test of significance for the parameter β1 at the 1% level.The null hypothesis shouldA) be rejected.
B) not be rejected.
C) be revised to test using F statistic.
D) be tested for β₃ instead.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
52
A regression analysis involved 10independent variables and 27 observations.The critical value of t for testing the significance of each of the independent variable's coefficients will have
A) 27 degrees of freedom.
B) 26 degrees of freedom.
C) 21 degrees of freedom.
D) 16 degrees of freedom.
A) 27 degrees of freedom.
B) 26 degrees of freedom.
C) 21 degrees of freedom.
D) 16 degrees of freedom.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
53
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 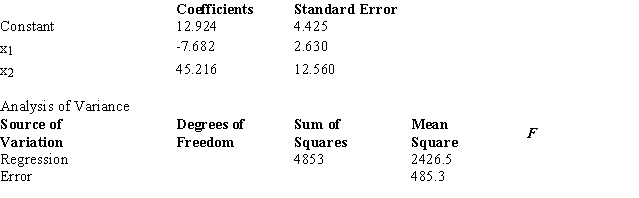 The t value obtained from the table which is used to test an individual parameter at the 1% level is
The t value obtained from the table which is used to test an individual parameter at the 1% level is
A) 2.650.
B) 2.921.
C) 2.977.
D) 3.012.
 The t value obtained from the table which is used to test an individual parameter at the 1% level is
The t value obtained from the table which is used to test an individual parameter at the 1% level isA) 2.650.
B) 2.921.
C) 2.977.
D) 3.012.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
54
In a multiple regression model involving 50 observations, the following estimated regression equation was obtained: 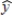 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.The critical F value at α = .05 is (using the conservative value from the table)
A) 2.53.
B) 2.69.
C) 2.61.
D) 2.99.
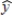 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.The critical F value at α = .05 is (using the conservative value from the table)
A) 2.53.
B) 2.69.
C) 2.61.
D) 2.99.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
55
In a multiple regression model involving 50 observations, the following estimated regression equation was obtained: 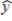 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.The computed F statistic for testing the significance of the above model is
A) 78.75.
B) 82.25.
C) 50.19.
D) 7.00.
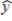 = 20 + 5x1 - 4x2 + 8x3 + 8x4
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100.The computed F statistic for testing the significance of the above model is
A) 78.75.
B) 82.25.
C) 50.19.
D) 7.00.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
56
In a multiple regression analysis involving 5 independent variables and 30 observations, SSR = 380 and SSE = 45.The multiple coefficient of determination is
A) .80.
B) .89.
C) .25.
D) .11.
A) .80.
B) .89.
C) .25.
D) .11.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
57
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 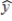 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.The coefficient of the unit price indicates that if the unit price is
A) increased by $1 (holding advertisement constant), sales are expected to increase by $4.
B) decreased by $1 (holding advertisement constant), sales are expected to decrease by $4.
C) increased by $1 (holding advertisement constant), sales are expected to increase by $4000.
D) increased by $1 (holding advertisement constant), sales are expected to decrease by $4000.
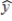 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.The coefficient of the unit price indicates that if the unit price is
A) increased by $1 (holding advertisement constant), sales are expected to increase by $4.
B) decreased by $1 (holding advertisement constant), sales are expected to decrease by $4.
C) increased by $1 (holding advertisement constant), sales are expected to increase by $4000.
D) increased by $1 (holding advertisement constant), sales are expected to decrease by $4000.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
58
In a multiple regression model involving 44 observations, the following estimated regression equation was obtained. 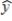 = 50 + 13x1 + 40x2 + 68x3
= 50 + 13x1 + 40x2 + 68x3
For this model, SSR = 600 and SSE = 400.The computed F statistic for testing the significance of the above model is
A) 28.00.
B) 20.00.
C) .600.
D) .667.
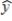 = 50 + 13x1 + 40x2 + 68x3
= 50 + 13x1 + 40x2 + 68x3
For this model, SSR = 600 and SSE = 400.The computed F statistic for testing the significance of the above model is
A) 28.00.
B) 20.00.
C) .600.
D) .667.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
59
In a multiple regression model involving 44 observations, the following estimated regression equation was obtained. 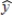 = 45+ 19x1 + 63x2 + 80x3
= 45+ 19x1 + 63x2 + 80x3
For this model, SSR = 800 and SSE = 200.The multiple coefficient of determination for the above model is
A) .667.
B) .800.
C) .336.
D) .200.
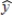 = 45+ 19x1 + 63x2 + 80x3
= 45+ 19x1 + 63x2 + 80x3
For this model, SSR = 800 and SSE = 200.The multiple coefficient of determination for the above model is
A) .667.
B) .800.
C) .336.
D) .200.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
60
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 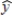 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.To test for the significance of the model, the test statistic F is
A) 19.83.
B) 88.23.
C) 17.
D) 2.33.
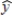 = 8 - 4x1 + 5x2
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20.To test for the significance of the model, the test statistic F is
A) 19.83.
B) 88.23.
C) 17.
D) 2.33.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
61
A regression model involving 4 independent variables and a sample of 15 observations resulted in the following sum of squares. SSR = 165
SSE = 60
The multiple coefficient of determination is
A) .3636.
B) .7333.
C) .275.
D) .5.
SSE = 60
The multiple coefficient of determination is
A) .3636.
B) .7333.
C) .275.
D) .5.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
62
Even though a residual may be unusually large, the standardized residual rule might fail to identify the observation as being an outlier.This difficulty can be circumvented by using
A) categorical independent variables.
B) residual transformation.
C) studentized deleted residuals.
D) logistic regression.
A) categorical independent variables.
B) residual transformation.
C) studentized deleted residuals.
D) logistic regression.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
63
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female).
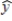 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.At the 5% level, the model
A) is significant.
B) is not significant.
C) would be significant if the sample size was larger than 30.
D) has significant individual parameters.
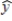 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.At the 5% level, the model
A) is significant.
B) is not significant.
C) would be significant if the sample size was larger than 30.
D) has significant individual parameters.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
64
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 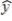 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.If we want to test for the significance of the model, the critical value of F at α = .05 is
A) 3.33.
B) 3.35.
C) 3.34.
D) 2.96.
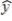 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.If we want to test for the significance of the model, the critical value of F at α = .05 is
A) 3.33.
B) 3.35.
C) 3.34.
D) 2.96.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
65
If an independent variable is added to a multiple regression model, the R2 value
A) becomes larger or smaller depending on the statistical significance of the variable.
B) becomes larger even if the variable added is not statistically significant.
C) might or might not become larger even if the variable added is statistically significant.
D) is not affected by the variable added even if it is statistically significant.
A) becomes larger or smaller depending on the statistical significance of the variable.
B) becomes larger even if the variable added is not statistically significant.
C) might or might not become larger even if the variable added is statistically significant.
D) is not affected by the variable added even if it is statistically significant.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
66
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 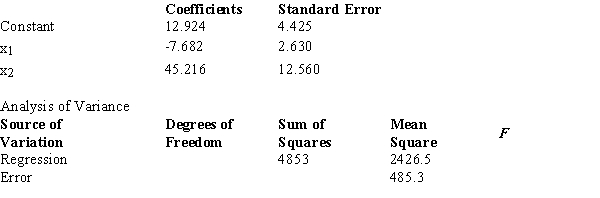 Carry out the test to determine if there is a relationship among the variables at the 1% level.The null hypothesis should
Carry out the test to determine if there is a relationship among the variables at the 1% level.The null hypothesis should
A) be rejected.
B) not be rejected.
C) be revised to test for multicollinearity.
D) test for individual significance instead.
 Carry out the test to determine if there is a relationship among the variables at the 1% level.The null hypothesis should
Carry out the test to determine if there is a relationship among the variables at the 1% level.The null hypothesis shouldA) be rejected.
B) not be rejected.
C) be revised to test for multicollinearity.
D) test for individual significance instead.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
67
A regression model involving 4 independent variables and a sample of 15 observations resulted in the following sum of squares. SSR = 165
SSE = 60
If we want to test for the significance of the model at a .05 level of significance, the critical F value (from the table) is
A) 3.06.
B) 3.48.
C) 3.34.
D) 3.11.
SSE = 60
If we want to test for the significance of the model at a .05 level of significance, the critical F value (from the table) is
A) 3.06.
B) 3.48.
C) 3.34.
D) 3.11.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
68
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 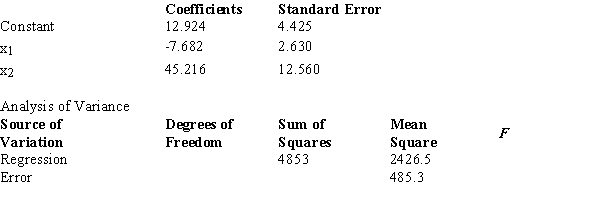 The test statistic used to determine if there is a relationship among the variables equals
The test statistic used to determine if there is a relationship among the variables equals
A) 1.40.
B) .2.
C) .77.
D) 5.
 The test statistic used to determine if there is a relationship among the variables equals
The test statistic used to determine if there is a relationship among the variables equalsA) 1.40.
B) .2.
C) .77.
D) 5.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
69
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female).  = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The test statistic for testing the significance of the model is
A) .73.
B) 1.47.
C) 28.69.
D) 5.22.
 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The test statistic for testing the significance of the model is
A) .73.
B) 1.47.
C) 28.69.
D) 5.22.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
70
A regression model involving 4 independent variables and a sample of 15 observations resulted in the following sum of squares. SSR = 165
SSE = 60
The test statistic obtained from the information provided is
A) 2.110.
B) 3.480.
C) 5.455.
D) 6.875.
SSE = 60
The test statistic obtained from the information provided is
A) 2.110.
B) 3.480.
C) 5.455.
D) 6.875.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
71
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 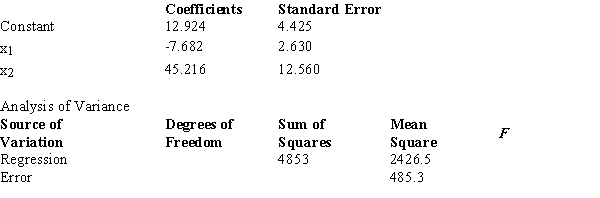 The F value obtained from the table which is used to test if there is a relationship among the variables at the 1% level equals
The F value obtained from the table which is used to test if there is a relationship among the variables at the 1% level equals
A) 3.41.
B) 3.63.
C) 5.74.
D) 3.81.
 The F value obtained from the table which is used to test if there is a relationship among the variables at the 1% level equals
The F value obtained from the table which is used to test if there is a relationship among the variables at the 1% level equalsA) 3.41.
B) 3.63.
C) 5.74.
D) 3.81.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
72
As the value of the multiple coefficient of determination increases,
A) the value of the adjusted multiple coefficient of determination decreases.
B) the value of the regression equation's constant b0 decreases.
C) the goodness of fit for the estimated multiple regression equation increases.
D) the value of the correlation coefficient decreases.
A) the value of the adjusted multiple coefficient of determination decreases.
B) the value of the regression equation's constant b0 decreases.
C) the goodness of fit for the estimated multiple regression equation increases.
D) the value of the correlation coefficient decreases.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
73
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 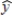 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The yearly income (in $) expected of a 24-year-old female individual is
A) $19.80.
B) $19,800.
C) $49.80.
D) $49,800.
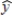 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The yearly income (in $) expected of a 24-year-old female individual is
A) $19.80.
B) $19,800.
C) $49.80.
D) $49,800.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
74
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 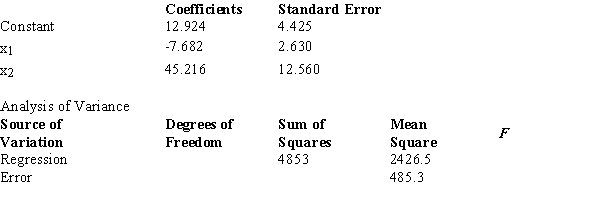 The sum of squares due to error (SSE) equals
The sum of squares due to error (SSE) equals
A) 373.31.
B) 485.3.
C) 4853.
D) 6308.9.
 The sum of squares due to error (SSE) equals
The sum of squares due to error (SSE) equalsA) 373.31.
B) 485.3.
C) 4853.
D) 6308.9.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
75
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 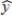 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The yearly income (in $) expected of a 24-year-old male individual is
A) $16,800.
B) $13,800.
C) $46,800.
D) $49,800.
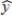 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The yearly income (in $) expected of a 24-year-old male individual is
A) $16,800.
B) $13,800.
C) $46,800.
D) $49,800.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
76
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 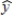 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The multiple coefficient of determination is
A) .32.
B) .42.
C) .68.
D) .50.
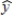 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The multiple coefficient of determination is
A) .32.
B) .42.
C) .68.
D) .50.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
77
A regression analysis involved 17 independent variables and 697 observations.The critical value of t for testing the significance of each of the independent variable's coefficients will have
A) 696 degrees of freedom.
B) 16 degrees of freedom.
C) 679 degrees of freedom.
D) 714 degrees of freedom.
A) 696 degrees of freedom.
B) 16 degrees of freedom.
C) 679 degrees of freedom.
D) 714 degrees of freedom.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
78
The _______ of an observation is determined by how far the values of the independent variables are from their means.
A) odds ratio
B) residual
C) collinearity
D) leverage
A) odds ratio
B) residual
C) collinearity
D) leverage

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
79
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 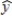 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The estimated income (in $) of a 30-year-old male is
A) $51,000.
B) $21.
C) $90,000.
D) $51.
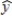 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.The estimated income (in $) of a 30-year-old male is
A) $51,000.
B) $21.
C) $90,000.
D) $51.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
80
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 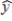 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.From the above linear function for multiple regression, it can be said that the expected yearly income of
A) males is $3 more than females.
B) females is $3 more than males.
C) males is $3000 more than females.
D) females is $3000 more than males.
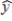 = 30 + .7x1 + 3x2
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384.From the above linear function for multiple regression, it can be said that the expected yearly income of
A) males is $3 more than females.
B) females is $3 more than males.
C) males is $3000 more than females.
D) females is $3000 more than males.

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck


