Deck 4: Applications of the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/184
Play
Full screen (f)
Deck 4: Applications of the Derivative
1
The owner of the Rancho Los Feliz has 2,600 yd of fencing material with which to enclose a rectangular piece of grazing land along the straight portion of a river.If fencing is not required along the river, what are the dimensions of the largest area that he can enclose? What is this area?
A)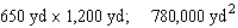
B)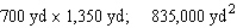
C)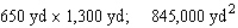
D)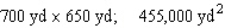
A)
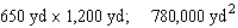
B)
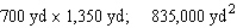
C)
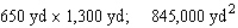
D)
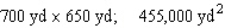
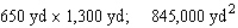
2
Phillip, the proprietor of a vineyard, estimates that the first 10,000 bottles of wine produced this season will fetch a profit of $2/bottle.However, the profit from each bottle beyond 10,000 drops by $0.0004 for each additional bottle sold. Assuming at least 10,000 bottles of wine are produced and sold, what is the maximum profit? What would be the price/bottle in this case?
A)The maximum profit is $40,500.00, the price/bottle is $3.20/bottle
B)The maximum profit is $22,500.00, the price/bottle is $3.00/bottle
C)The maximum profit is $28,500.00,the price/bottle is $3.00/bottle
D)The maximum profit is $46,500.00, the price/bottle is $3.40/bottle
E)The maximum profit is $34,500.00, the price/bottle is $3.10/bottle
A)The maximum profit is $40,500.00, the price/bottle is $3.20/bottle
B)The maximum profit is $22,500.00, the price/bottle is $3.00/bottle
C)The maximum profit is $28,500.00,the price/bottle is $3.00/bottle
D)The maximum profit is $46,500.00, the price/bottle is $3.40/bottle
E)The maximum profit is $34,500.00, the price/bottle is $3.10/bottle
The maximum profit is $22,500.00, the price/bottle is $3.00/bottle
3
An apple orchard has an average yield of 48 bushels of apples/tree if tree density is 26 trees/acre.For each unit increase in tree density, the yield decreases by 3 bushels.How many trees should be planted in order to maximize the yield?
A)23
B)24
C)22
D)21
A)23
B)24
C)22
D)21
21
4
A Norman window has the shape of a rectangle surmounted by a semicircle (see the accompanying figure).If a Norman window is to have a perimeter of 28 ft, what should its dimensions be in order to allow the maximum amount of light through the window? 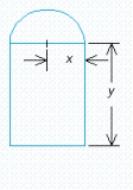
A)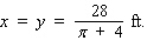
B)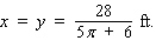
C)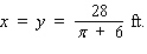
D)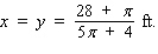

A)
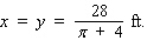
B)
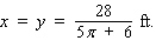
C)
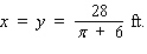
D)
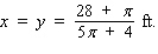

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
5
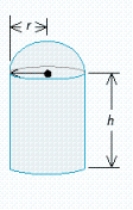
A cylindrical container for storing radioactive waste is to be constructed from lead and have a thickness of 6 in.(see the figure).If the volume of the outside cylinder is to be 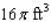 , find the radius and the height of the inside cylinder that will result in a container of maximum storage capacity.
, find the radius and the height of the inside cylinder that will result in a container of maximum storage capacity. 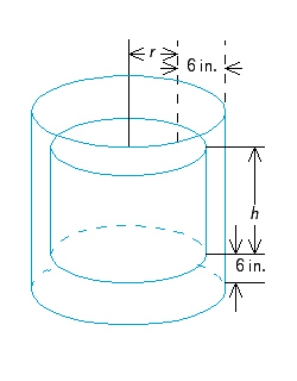 Hint: Show that the storage capacity (inside volume) is given by
Hint: Show that the storage capacity (inside volume) is given by 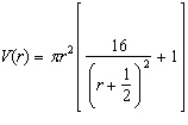
A)r =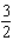 ft.; h = 2 ft.
ft.; h = 2 ft.
B)r =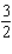 ft.; h = 3 ft.
ft.; h = 3 ft.
C)r =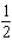 ft.; h = 2 ft.
ft.; h = 2 ft.
D)r =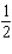 ft.; h = 3 ft.
ft.; h = 3 ft.
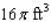 , find the radius and the height of the inside cylinder that will result in a container of maximum storage capacity.
, find the radius and the height of the inside cylinder that will result in a container of maximum storage capacity.  Hint: Show that the storage capacity (inside volume) is given by
Hint: Show that the storage capacity (inside volume) is given by 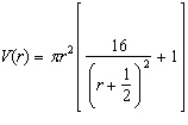
A)r =
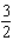 ft.; h = 2 ft.
ft.; h = 2 ft.B)r =
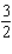 ft.; h = 3 ft.
ft.; h = 3 ft.C)r =
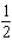 ft.; h = 2 ft.
ft.; h = 2 ft.D)r =
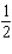 ft.; h = 3 ft.
ft.; h = 3 ft.
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
6
A book designer has decided that the pages of a book should have 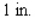 margins at the top and bottom and
margins at the top and bottom and 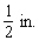 margins on the sides.She further stipulated that each page should have an area of
margins on the sides.She further stipulated that each page should have an area of 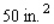 (see the figure).
(see the figure). 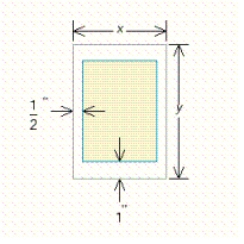 Determine the page dimensions that will result in the maximum printed area on the page.
Determine the page dimensions that will result in the maximum printed area on the page.
A)
B)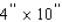
C)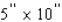
D)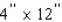
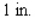 margins at the top and bottom and
margins at the top and bottom and 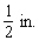 margins on the sides.She further stipulated that each page should have an area of
margins on the sides.She further stipulated that each page should have an area of 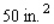 (see the figure).
(see the figure).  Determine the page dimensions that will result in the maximum printed area on the page.
Determine the page dimensions that will result in the maximum printed area on the page.A)
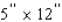
B)
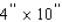
C)
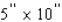
D)
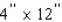

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
7
A grain silo has the shape of a right circular cylinder surmounted by a hemisphere (see the figure).If the silo is to have a capacity of 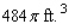 , find the radius and height of the silo that requires the least amount of material to construct. Hint: The volume of the silo is
, find the radius and height of the silo that requires the least amount of material to construct. Hint: The volume of the silo is 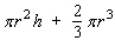 , and the surface area (including the floor) is
, and the surface area (including the floor) is 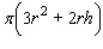 .
. 
A)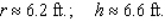
B)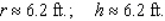
C)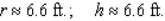
D)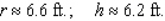
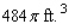 , find the radius and height of the silo that requires the least amount of material to construct. Hint: The volume of the silo is
, find the radius and height of the silo that requires the least amount of material to construct. Hint: The volume of the silo is 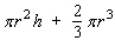 , and the surface area (including the floor) is
, and the surface area (including the floor) is 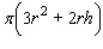 .
. 
A)
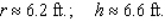
B)
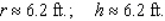
C)
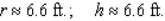
D)
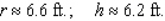

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
8
The management of the UNICO department store has decided to enclose an 300  area outside the building for displaying potted plants and flowers.One side will be formed by the external wall of the store, two sides will be constructed of pine boards, and the fourth side will be made of galvanized steel fencing material.
area outside the building for displaying potted plants and flowers.One side will be formed by the external wall of the store, two sides will be constructed of pine boards, and the fourth side will be made of galvanized steel fencing material. 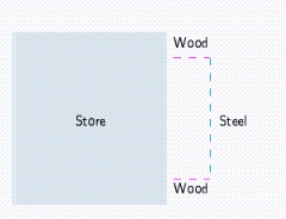 If the pine board fencing costs $6/running foot and the steel fencing costs $2/running foot, determine the dimensions of the enclosure that can be erected at minimum cost.
If the pine board fencing costs $6/running foot and the steel fencing costs $2/running foot, determine the dimensions of the enclosure that can be erected at minimum cost.
A)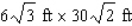
B)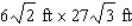
C)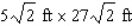
D)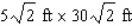
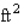 area outside the building for displaying potted plants and flowers.One side will be formed by the external wall of the store, two sides will be constructed of pine boards, and the fourth side will be made of galvanized steel fencing material.
area outside the building for displaying potted plants and flowers.One side will be formed by the external wall of the store, two sides will be constructed of pine boards, and the fourth side will be made of galvanized steel fencing material.  If the pine board fencing costs $6/running foot and the steel fencing costs $2/running foot, determine the dimensions of the enclosure that can be erected at minimum cost.
If the pine board fencing costs $6/running foot and the steel fencing costs $2/running foot, determine the dimensions of the enclosure that can be erected at minimum cost.A)
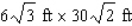
B)
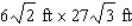
C)
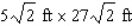
D)
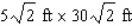

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
9
A rectangular box is to have a square base and a volume of 32 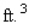 .If the material for the base costs 10 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 20 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
.If the material for the base costs 10 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 20 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 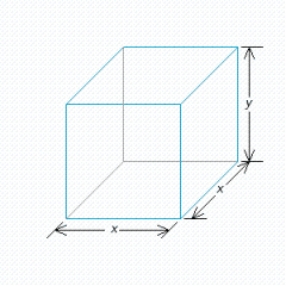
A)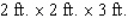
B)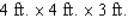
C)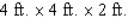
D)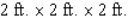
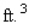 .If the material for the base costs 10 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 20 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
.If the material for the base costs 10 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 20 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 
A)
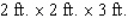
B)
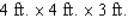
C)
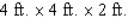
D)
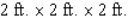

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
10
For its beef stew, Betty Moore Company uses aluminum containers that have the form of right circular cylinders.Find the radius and height of a container if it has a capacity of 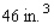 and is constructed using the least amount of metal.
and is constructed using the least amount of metal.
A)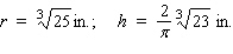
B)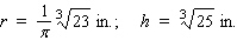
C)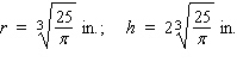
D)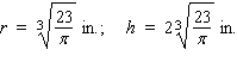
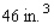 and is constructed using the least amount of metal.
and is constructed using the least amount of metal.A)
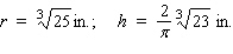
B)
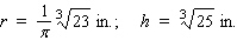
C)
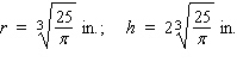
D)
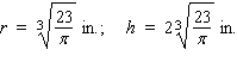

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
11
In the diagram, S represents the position of a power relay station located on a straight coast, and E shows the location of a marine biology experimental station on an island.A cable is to be laid connecting the relay station with the experimental station. 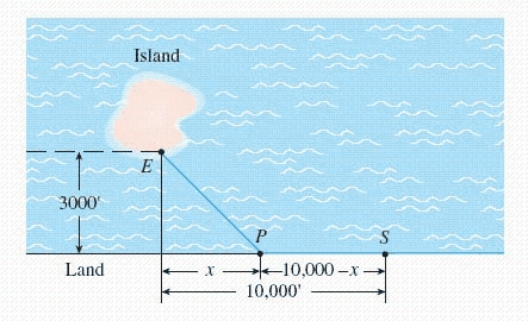 If the cost of running the cable on land is $2.50/running foot and the cost of running the cable under water is $6.50/running foot, locate the point P that will result in a minimum cost (solve for x).
If the cost of running the cable on land is $2.50/running foot and the cost of running the cable under water is $6.50/running foot, locate the point P that will result in a minimum cost (solve for x).
A)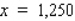 ft
ft
B)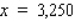 ft
ft
C)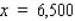 ft
ft
D)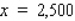 ft
ft
E)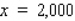 ft
ft
 If the cost of running the cable on land is $2.50/running foot and the cost of running the cable under water is $6.50/running foot, locate the point P that will result in a minimum cost (solve for x).
If the cost of running the cable on land is $2.50/running foot and the cost of running the cable under water is $6.50/running foot, locate the point P that will result in a minimum cost (solve for x).A)
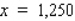 ft
ftB)
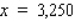 ft
ftC)
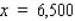 ft
ftD)
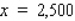 ft
ftE)
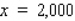 ft
ft
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
12
A truck gets 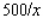 mpg when driven at a constant speed of x mph (between 40 and 80 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 40 and 80 mph is it most economical to drive?
mpg when driven at a constant speed of x mph (between 40 and 80 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 40 and 80 mph is it most economical to drive?
A)60 mph
B)80 mph
C)40 mph
D)75 mph
E)45 mph
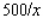 mpg when driven at a constant speed of x mph (between 40 and 80 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 40 and 80 mph is it most economical to drive?
mpg when driven at a constant speed of x mph (between 40 and 80 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 40 and 80 mph is it most economical to drive?A)60 mph
B)80 mph
C)40 mph
D)75 mph
E)45 mph

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
13
The owner of a luxury motor yacht that sails among the 4,000 Greek islands charges $600/person/day if exactly 20 people sign up for the cruise.However,if more than 20 people sign up (up to the maximum capacity of 90) for the cruise, then each fare is reduced by $4 for each additional passenger. Assuming at least 20 people sign up for the cruise, determine how many passengers will result in the maximum revenue for the owner of the yacht.What is the maximum revenue? What would be the fare/passenger in this case?
A)85; $28,400; $340
B)90; $28,900; $350
C)90; $28,400; $350
D)85; $28,900; $340
A)85; $28,400; $340
B)90; $28,900; $350
C)90; $28,400; $350
D)85; $28,900; $340

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
14
The demand for motorcycle tires imported by Dixie Import-Export is 40,000/year and may be assumed to be uniform throughout the year.The cost of ordering a shipment of tires is $400, and the cost of storing each tire for a year is $2. Determine how many tires should be in each shipment if the ordering and storage costs are to be minimized.(Assume that each shipment arrives just as the previous one has been sold.)
A)5,500
B)4,000
C)3,500
D)3,000
A)5,500
B)4,000
C)3,500
D)3,000

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
15
What are the dimensions of a closed rectangular box that has a square cross section, a capacity of 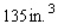 and is constructed using the least amount of material?
and is constructed using the least amount of material?
A)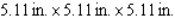
B)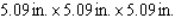
C)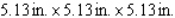
D)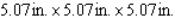
E)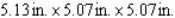
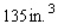 and is constructed using the least amount of material?
and is constructed using the least amount of material?A)
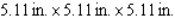
B)
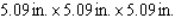
C)
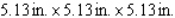
D)
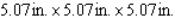
E)
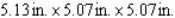

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
16
If exactly 150 people sign up for a charter flight, Leisure World Travel Agency charges $250/person.However, if more than 150 people sign up for the flight (assume this is the case), then each fare is reduced by $1 for each additional person. Determine how many passengers will result in a maximum revenue for the travel agency.What is the maximum revenue? What would be the fare per passenger in this case?
Hint: Let x denote the number of passengers above 150.Show that the revenue function R is given by R(x) = (150 + x)(250 - x).
A)250; $39,000; $250
B)200; $40,000; $200
C)200; $39,000; $200
D)250; $40,000; $250
Hint: Let x denote the number of passengers above 150.Show that the revenue function R is given by R(x) = (150 + x)(250 - x).
A)250; $39,000; $250
B)200; $40,000; $200
C)200; $39,000; $200
D)250; $40,000; $250

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
17
By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made.If the cardboard is 8 in.long and 3 in.wide, find the dimensions of the box that will yield the maximum volume.
A)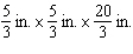
B)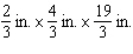
C)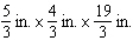
D)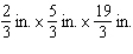
E)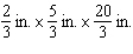
A)
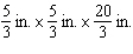
B)
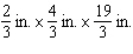
C)
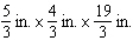
D)
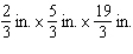
E)
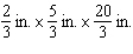

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
18
Postal regulations specify that a parcel sent by parcel post may have a combined length and girth of no more than 102 in.Find the dimensions of a rectangular package that has a square cross section and the largest volume that may be sent through the mail.What is the volume of such a package? (Hint: The length plus the girth is 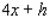 (see the figure)).
(see the figure)). 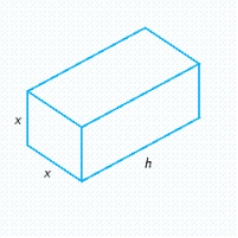
A)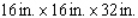 ,
, 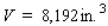
B)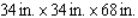 ,
, 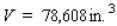
C)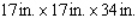 ,
, 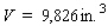
D)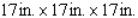 ,
, 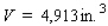
E)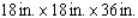 ,
, 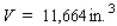
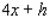 (see the figure)).
(see the figure)). 
A)
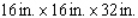 ,
, 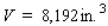
B)
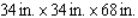 ,
, 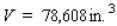
C)
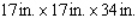 ,
, 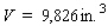
D)
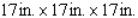 ,
, 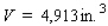
E)
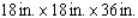 ,
, 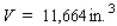

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
19
If an open box has a square base and a volume of 500 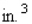 and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.
and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.
A)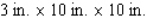
B)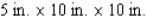
C)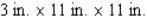
D)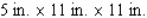
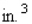 and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.
and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.A)
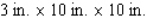
B)
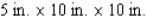
C)
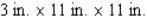
D)
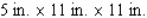

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
20
A wooden beam has a rectangular cross section of height 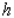 in.and width
in.and width 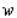 in.(see the figure).The strength
in.(see the figure).The strength 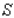 of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross section of the strongest beam that can be cut from a round log of diameter 24 in.? Hint:
of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross section of the strongest beam that can be cut from a round log of diameter 24 in.? Hint: 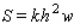 , where
, where 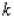 is a constant of proportionality.
is a constant of proportionality. 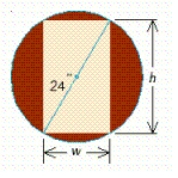
A)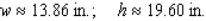
B)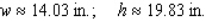
C)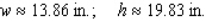
D)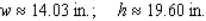
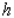 in.and width
in.and width 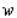 in.(see the figure).The strength
in.(see the figure).The strength 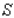 of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross section of the strongest beam that can be cut from a round log of diameter 24 in.? Hint:
of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross section of the strongest beam that can be cut from a round log of diameter 24 in.? Hint: 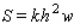 , where
, where 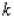 is a constant of proportionality.
is a constant of proportionality. 
A)
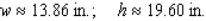
B)
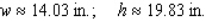
C)
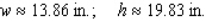
D)
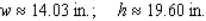

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
21
What are the dimensions of a closed rectangular box that has a square cross section, a capacity of 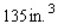 and is constructed using the least amount of material? Round the answer to two decimal places.
and is constructed using the least amount of material? Round the answer to two decimal places. 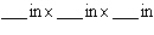
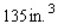 and is constructed using the least amount of material? Round the answer to two decimal places.
and is constructed using the least amount of material? Round the answer to two decimal places. 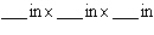

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
22
An apple orchard has an average yield of 48 bushels of apples/tree if tree density is 24 trees/acre.For each unit increase in tree density, the yield decreases by 3 bushels.How many trees should be planted in order to maximize the yield?
__________ trees
__________ trees

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
23
The demand for motorcycle tires imported by Dixie Import-Export is 30,000/year and may be assumed to be uniform throughout the year.The cost of ordering a shipment of tires is $300, and the cost of storing each tire for a year is $2.
Determine how many tires should be in each shipment if the ordering and storage costs are to be minimized.(Assume that each shipment arrives just as the previous one has been sold.)
__________ tires
Determine how many tires should be in each shipment if the ordering and storage costs are to be minimized.(Assume that each shipment arrives just as the previous one has been sold.)
__________ tires

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
24
Neilsen Cookie Company sells its assorted butter cookies in containers that have a net content of 1 lb.The estimated demand for the cookies is 1,000,000 1-lb containers.The setup cost for each production run is $250, and the manufacturing cost is $.50 for each container of cookies.The cost of storing each container of cookies over the year is $.20.
Assuming uniformity of demand throughout the year and instantaneous production, how many containers of cookies should Neilsen produce per production run in order to minimize the production cost?
Hint: Show that the total production cost is given by the function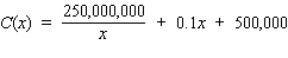 .
.
Then minimize the function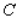 on the interval (0, 1,000,000).
on the interval (0, 1,000,000).
__________ containers of cookies per production run
Assuming uniformity of demand throughout the year and instantaneous production, how many containers of cookies should Neilsen produce per production run in order to minimize the production cost?
Hint: Show that the total production cost is given by the function
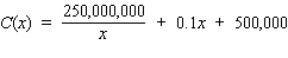 .
.Then minimize the function
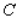 on the interval (0, 1,000,000).
on the interval (0, 1,000,000).__________ containers of cookies per production run

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
25
A rectangular box is to have a square base and a volume of 4  .If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
.If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 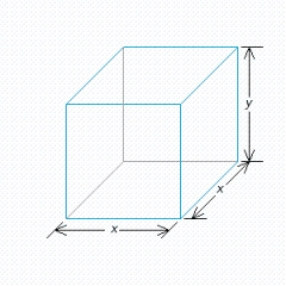
 .If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
.If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 
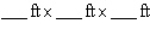

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
26
Phillip, the proprietor of a vineyard, estimates that the first 10,000 bottles of wine produced this season will fetch a profit of $2/bottle.However, the profit from each bottle beyond 10,000 drops by $0.0002 for each additional bottle sold.Assuming at least 10,000 bottles of wine are produced and sold, what is the maximum profit? Round the answer to two decimal places.
The maximum profit is $__________
What would be the price/bottle in this case? Round the answer to the nearest cent.
$__________/bottle
The maximum profit is $__________
What would be the price/bottle in this case? Round the answer to the nearest cent.
$__________/bottle

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
27
Find the dimensions of a rectangle with a perimeter of 200 ft that has the largest possible area.
A)Dimensions are 100 ft.by 75 ft.
B)Dimensions are 65 ft.by 70 ft.
C)Dimensions are 65 ft.by 75 ft.
D)Dimensions are 60 ft.by 60 ft.
E)Dimensions are 50 ft.by 50 ft.
A)Dimensions are 100 ft.by 75 ft.
B)Dimensions are 65 ft.by 70 ft.
C)Dimensions are 65 ft.by 75 ft.
D)Dimensions are 60 ft.by 60 ft.
E)Dimensions are 50 ft.by 50 ft.

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
28
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 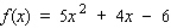
A)Absolute maximum value: none; absolute minimum value: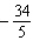
B)Absolute maximum value: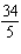 ; absolute minimum value: none
; absolute minimum value: none
C)Absolute maximum value: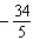 ; absolute minimum value: none
; absolute minimum value: none
D)No absolute extrema
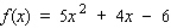
A)Absolute maximum value: none; absolute minimum value:
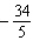
B)Absolute maximum value:
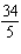 ; absolute minimum value: none
; absolute minimum value: noneC)Absolute maximum value:
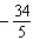 ; absolute minimum value: none
; absolute minimum value: noneD)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
29
You are given the graph of some function f defined on the indicated interval.Find the absolute maximum and the absolute minimum of f, if they exist. 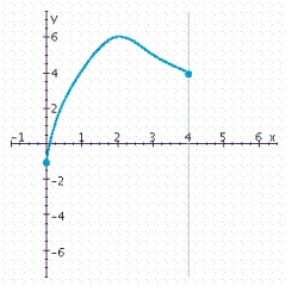
A)Absolute maximum value: 6; absolute minimum value: 0
B)Absolute maximum value: 4; absolute minimum value: - 1
C)Absolute maximum value: 3; absolute minimum value: - 1
D)Absolute maximum value: 6; absolute minimum value: - 1

A)Absolute maximum value: 6; absolute minimum value: 0
B)Absolute maximum value: 4; absolute minimum value: - 1
C)Absolute maximum value: 3; absolute minimum value: - 1
D)Absolute maximum value: 6; absolute minimum value: - 1

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
30
By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made.If the cardboard is 8 in.long and 3 in.wide, find the dimensions of the box that will yield the maximum volume. 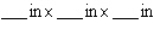

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
31
If an open box has a square base and a volume of 864 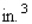 and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.
and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction. 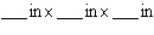
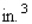 and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.
and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction. 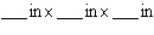

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
32
You are given the graph of some function f defined on the indicated interval.Find the absolute maximum and the absolute minimum of f, if they exist. 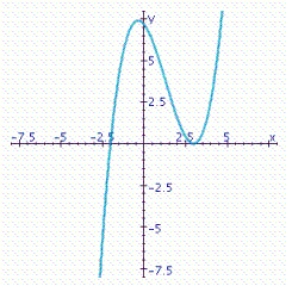
A)Absolute maximum value: none; absolute minimum value: 0
B)Absolute maximum value: 7.4; absolute minimum value: none
C)Absolute maximum value: none; absolute minimum value: none
D)Absolute maximum value: 7.4; absolute minimum value: 0

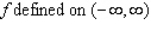
A)Absolute maximum value: none; absolute minimum value: 0
B)Absolute maximum value: 7.4; absolute minimum value: none
C)Absolute maximum value: none; absolute minimum value: none
D)Absolute maximum value: 7.4; absolute minimum value: 0

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
33
A book designer has decided that the pages of a book should have 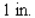 margins at the top and bottom and
margins at the top and bottom and 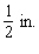 margins on the sides.She further stipulated that each page should have an area of
margins on the sides.She further stipulated that each page should have an area of 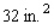 (see the figure).
(see the figure). 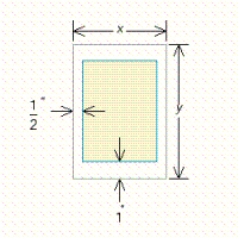 Determine the page dimensions that will result in the maximum printed area on the page.
Determine the page dimensions that will result in the maximum printed area on the page. 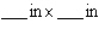
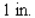 margins at the top and bottom and
margins at the top and bottom and 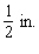 margins on the sides.She further stipulated that each page should have an area of
margins on the sides.She further stipulated that each page should have an area of 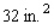 (see the figure).
(see the figure).  Determine the page dimensions that will result in the maximum printed area on the page.
Determine the page dimensions that will result in the maximum printed area on the page. 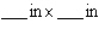

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
34
Find the dimensions of a rectangle of area 144 sq ft that has the smallest possible perimeter.
A)Dimensions are 13 ft.by 11 ft.
B)Dimensions are 15ft.by 14 ft.
C)Dimensions are 12 ft.by 12 ft.
D)Dimensions are 10 ft.by 14 ft.
E)Dimensions are 9 ft.by 13 ft.
A)Dimensions are 13 ft.by 11 ft.
B)Dimensions are 15ft.by 14 ft.
C)Dimensions are 12 ft.by 12 ft.
D)Dimensions are 10 ft.by 14 ft.
E)Dimensions are 9 ft.by 13 ft.

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
35
The figure depicts a racetrack with ends that are semicircular in shape.The length of the track is 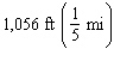 .
.  Find
Find 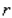 and
and 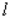 so that the area enclosed by the rectangular region of the racetrack is as large as possible.
so that the area enclosed by the rectangular region of the racetrack is as large as possible.
A)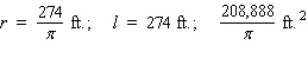
B)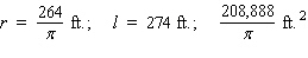
C)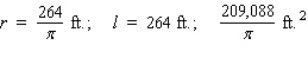
D)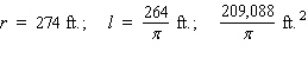
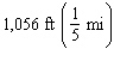 .
.  Find
Find 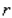 and
and 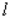 so that the area enclosed by the rectangular region of the racetrack is as large as possible.
so that the area enclosed by the rectangular region of the racetrack is as large as possible.A)
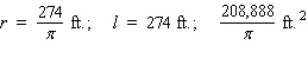
B)
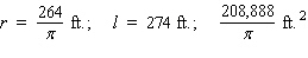
C)
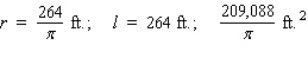
D)
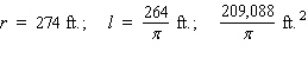

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
36
The owner of the Rancho Los Feliz has 3,000 yd of fencing material with which to enclose a rectangular piece of grazing land along the straight portion of a river.
If fencing is not required along the river, what are the dimensions of the largest area that he can enclose?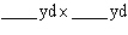 What is this area?
What is this area?
__________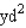
If fencing is not required along the river, what are the dimensions of the largest area that he can enclose?
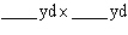 What is this area?
What is this area?__________
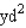

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
37
Neilsen Cookie Company sells its assorted butter cookies in containers that have a net content of 1 lb.The estimated demand for the cookies is 1,000,000 1-lb containers.The setup cost for each production run is $250, and the manufacturing cost is $.30 for each container of cookies.The cost of storing each container of cookies over the year is $.20. Assuming uniformity of demand throughout the year and instantaneous production, how many containers of cookies should Neilsen produce per production run in order to minimize the production cost?
Hint: Show that the total production cost is given by the function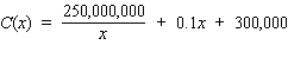 .
.
Then minimize the function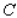 on the interval (0, 1,000,000).
on the interval (0, 1,000,000).
A)50,000
B)40,000
C)45,000
D)35,000
Hint: Show that the total production cost is given by the function
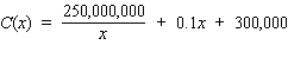 .
.Then minimize the function
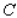 on the interval (0, 1,000,000).
on the interval (0, 1,000,000).A)50,000
B)40,000
C)45,000
D)35,000

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
38
A truck gets 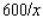 mpg when driven at a constant speed of x mph (between 50 and 70 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 50 and 70 mph is it most economical to drive?
mpg when driven at a constant speed of x mph (between 50 and 70 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 50 and 70 mph is it most economical to drive?
__________ mph
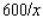 mpg when driven at a constant speed of x mph (between 50 and 70 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 50 and 70 mph is it most economical to drive?
mpg when driven at a constant speed of x mph (between 50 and 70 mph).If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 50 and 70 mph is it most economical to drive?__________ mph

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
39
Postal regulations specify that a parcel sent by parcel post may have a combined length and girth of no more than 84 in.
Find the dimensions of a rectangular package that has a square cross section and the largest volume that may be sent through the mail.Hint: The length plus the girth is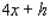 (see the figure).
(see the figure).
Dimensions: _____ x _____ x _____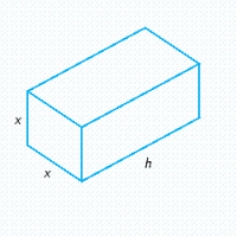 What is the volume of such a package?
What is the volume of such a package? 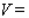 __________
__________ 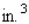
Find the dimensions of a rectangular package that has a square cross section and the largest volume that may be sent through the mail.Hint: The length plus the girth is
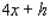 (see the figure).
(see the figure).Dimensions: _____ x _____ x _____
 What is the volume of such a package?
What is the volume of such a package? 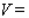 __________
__________ 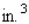

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
40
In the diagram, S represents the position of a power relay station located on a straight coast, and E shows the location of a marine biology experimental station on an island.A cable is to be laid connecting the relay station with the experimental station. 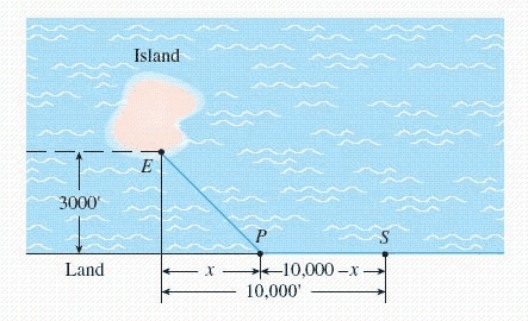 If the cost of running the cable on land is $3.60/running foot and the cost of running the cable under water is $6.00/running foot, locate the point P that will result in a minimum cost (solve for x).
If the cost of running the cable on land is $3.60/running foot and the cost of running the cable under water is $6.00/running foot, locate the point P that will result in a minimum cost (solve for x).  __________ ft
__________ ft
 If the cost of running the cable on land is $3.60/running foot and the cost of running the cable under water is $6.00/running foot, locate the point P that will result in a minimum cost (solve for x).
If the cost of running the cable on land is $3.60/running foot and the cost of running the cable under water is $6.00/running foot, locate the point P that will result in a minimum cost (solve for x).  __________ ft
__________ ft
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
41
Find the absolute maximum value and the absolute minimum value, if any, of the function. 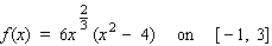
A)Absolute maximum value: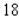 ; absolute minimum value:
; absolute minimum value:
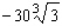
B)Absolute maximum value: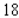 ; absolute minimum value:
; absolute minimum value:
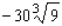
C)Absolute maximum value: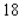 ; absolute minimum value:
; absolute minimum value:
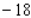
D)Absolute maximum value: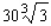 ; absolute minimum value:
; absolute minimum value:
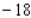
E)Absolute maximum value: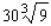 ; absolute minimum value:
; absolute minimum value:
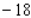
A)Absolute maximum value:
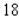 ; absolute minimum value:
; absolute minimum value: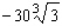
B)Absolute maximum value:
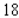 ; absolute minimum value:
; absolute minimum value: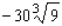
C)Absolute maximum value:
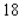 ; absolute minimum value:
; absolute minimum value: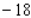
D)Absolute maximum value:
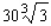 ; absolute minimum value:
; absolute minimum value: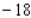
E)Absolute maximum value:
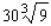 ; absolute minimum value:
; absolute minimum value: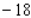

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose the quantity demanded per week of a certain dress is related to the unit price p by the demand equation 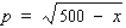 , where p is in dollars and x is the number of dresses made. To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px).Round the answer to the nearest integer.
, where p is in dollars and x is the number of dresses made. To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px).Round the answer to the nearest integer.
A)333 dresses
B)330 dresses
C)335 dresses
D)338 dresses
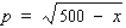 , where p is in dollars and x is the number of dresses made. To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px).Round the answer to the nearest integer.
, where p is in dollars and x is the number of dresses made. To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px).Round the answer to the nearest integer.A)333 dresses
B)330 dresses
C)335 dresses
D)338 dresses

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
43
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 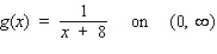
A)Absolute maximum value: ; absolute minimum value:
; absolute minimum value:
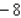
B)Absolute maximum value: ; absolute minimum value:
; absolute minimum value:

C)Absolute maximum value: none; absolute minimum value:
D)No absolute extrema
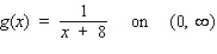
A)Absolute maximum value:
 ; absolute minimum value:
; absolute minimum value: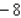
B)Absolute maximum value:
 ; absolute minimum value:
; absolute minimum value:
C)Absolute maximum value: none; absolute minimum value:

D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
44
Find the absolute maximum value and the absolute minimum value, if any, of the given function. ![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e26_b394_c52cc33db7be_TB7866_11.jpg) on [1, 5]
on [1, 5]
A)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e27_b394_e9067dc29a5e_TB7866_11.jpg) ; Absolute minimum value: 3
; Absolute minimum value: 3
B)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e28_b394_9385f43946d0_TB7866_11.jpg) ; Absolute minimum value:
; Absolute minimum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e29_b394_07c4ea87b133_TB7866_11.jpg)
C)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_a53a_b394_b7b8ca2cd430_TB7866_11.jpg) ; Absolute minimum value: 3
; Absolute minimum value: 3
D)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_a53b_b394_33bbe42cf095_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4
E)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_a53c_b394_699c80ec3814_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e26_b394_c52cc33db7be_TB7866_11.jpg) on [1, 5]
on [1, 5]A)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e27_b394_e9067dc29a5e_TB7866_11.jpg) ; Absolute minimum value: 3
; Absolute minimum value: 3B)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e28_b394_9385f43946d0_TB7866_11.jpg) ; Absolute minimum value:
; Absolute minimum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_7e29_b394_07c4ea87b133_TB7866_11.jpg)
C)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_a53a_b394_b7b8ca2cd430_TB7866_11.jpg) ; Absolute minimum value: 3
; Absolute minimum value: 3D)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_a53b_b394_33bbe42cf095_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4E)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]</strong> A)Absolute maximum value: ; Absolute minimum value: 3 B)Absolute maximum value: ; Absolute minimum value: C)Absolute maximum value: ; Absolute minimum value: 3 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value: 4](https://storage.examlex.com/TB7866/11eb12b0_a9e4_a53c_b394_699c80ec3814_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
45
Find the absolute maximum value and the absolute minimum value, if any, of the given function. ![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_2fff_b394_8de900d82758_TB7866_11.jpg) on [1, 4]
on [1, 4]
A)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_3000_b394_57b18df8d387_TB7866_11.jpg) ; Absolute minimum value: 5
; Absolute minimum value: 5
B)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5711_b394_6318882721e6_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4
C)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5712_b394_2d2860079dce_TB7866_11.jpg) ; Absolute minimum value: 5
; Absolute minimum value: 5
D)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5713_b394_e9818c09693f_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4
E)Absolute maximum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5714_b394_8583a447e533_TB7866_11.jpg) ; Absolute minimum value:
; Absolute minimum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5715_b394_39c35ee43b78_TB7866_11.jpg)
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_2fff_b394_8de900d82758_TB7866_11.jpg) on [1, 4]
on [1, 4]A)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_3000_b394_57b18df8d387_TB7866_11.jpg) ; Absolute minimum value: 5
; Absolute minimum value: 5B)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5711_b394_6318882721e6_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4C)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5712_b394_2d2860079dce_TB7866_11.jpg) ; Absolute minimum value: 5
; Absolute minimum value: 5D)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5713_b394_e9818c09693f_TB7866_11.jpg) ; Absolute minimum value: 4
; Absolute minimum value: 4E)Absolute maximum value:
![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5714_b394_8583a447e533_TB7866_11.jpg) ; Absolute minimum value:
; Absolute minimum value:![<strong>Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 4]</strong> A)Absolute maximum value: ; Absolute minimum value: 5 B)Absolute maximum value: ; Absolute minimum value: 4 C)Absolute maximum value: ; Absolute minimum value: 5 D)Absolute maximum value: ; Absolute minimum value: 4 E)Absolute maximum value: ; Absolute minimum value:](https://storage.examlex.com/TB7866/11eb12b0_a9e4_5715_b394_39c35ee43b78_TB7866_11.jpg)

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
46
A division of Chapman Corporation manufactures a pager.The weekly fixed cost for the division is $20,000, and the variable cost for producing x pagers/week is 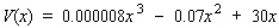 dollars. The company realizes a revenue of
dollars. The company realizes a revenue of 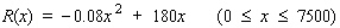 dollars from the sale of x pagers/week.
dollars from the sale of x pagers/week.
Find the level of production that will yield a maximum profit for the manufacturer.(Hint: Use the quadratic formula.)
A)1,316 pagers/week
B)1,666 pagers/week
C)1,616 pagers/week
D)1,542 pagers/week
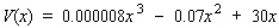 dollars. The company realizes a revenue of
dollars. The company realizes a revenue of 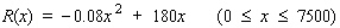 dollars from the sale of x pagers/week.
dollars from the sale of x pagers/week.Find the level of production that will yield a maximum profit for the manufacturer.(Hint: Use the quadratic formula.)
A)1,316 pagers/week
B)1,666 pagers/week
C)1,616 pagers/week
D)1,542 pagers/week

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
47
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 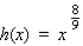
A)Absolute maximum value: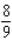 ; absolute minimum value: none
; absolute minimum value: none
B)Absolute maximum value: none; absolute minimum value: 0
C)Absolute maximum value: none; absolute minimum value: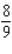
D)No absolute extrema
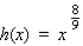
A)Absolute maximum value:
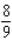 ; absolute minimum value: none
; absolute minimum value: noneB)Absolute maximum value: none; absolute minimum value: 0
C)Absolute maximum value: none; absolute minimum value:
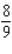
D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
48
Find the absolute maximum value and the absolute minimum value, if any, of the function. 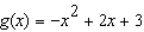
A)Absolute maximum value: 3; Absolute minimum value: 4
B)Absolute maximum value: 4; Absolute minimum value: none
C)Absolute maximum value: none; Absolute minimum value: 4
D)Absolute maximum value: 2; Absolute minimum value: 3
E)g(x) has no absolute extrema
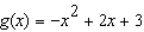
A)Absolute maximum value: 3; Absolute minimum value: 4
B)Absolute maximum value: 4; Absolute minimum value: none
C)Absolute maximum value: none; Absolute minimum value: 4
D)Absolute maximum value: 2; Absolute minimum value: 3
E)g(x) has no absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
49
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 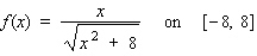
A)Absolute maximum value: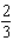 ; absolute minimum value:
; absolute minimum value:
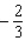
B)Absolute maximum value: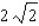 ; absolute minimum value:
; absolute minimum value:
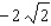
C)Absolute maximum value: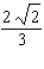 ; absolute minimum value:
; absolute minimum value:
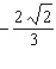
D)No absolute extrema
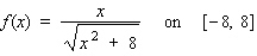
A)Absolute maximum value:
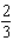 ; absolute minimum value:
; absolute minimum value: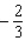
B)Absolute maximum value:
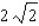 ; absolute minimum value:
; absolute minimum value: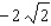
C)Absolute maximum value:
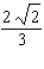 ; absolute minimum value:
; absolute minimum value: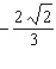
D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
50
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 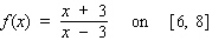
A)Absolute maximum value: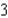 ; absolute minimum value:
; absolute minimum value:
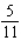
B)Absolute maximum value: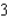 ; absolute minimum value:
; absolute minimum value:
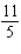
C)Absolute maximum value: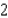 ; absolute minimum value:
; absolute minimum value:
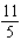
D)No absolute extrema
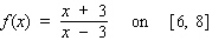
A)Absolute maximum value:
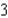 ; absolute minimum value:
; absolute minimum value: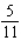
B)Absolute maximum value:
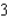 ; absolute minimum value:
; absolute minimum value: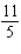
C)Absolute maximum value:
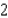 ; absolute minimum value:
; absolute minimum value: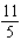
D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
51
A stone is thrown straight up from the roof of a 50-ft building.The height (in feet) of the stone at any time t (in seconds), measured from the ground, is given by 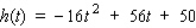 What is the maximum height the stone reaches?
What is the maximum height the stone reaches?
A)99 ft
B)92 ft
C)110 ft
D)96 ft
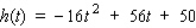 What is the maximum height the stone reaches?
What is the maximum height the stone reaches?A)99 ft
B)92 ft
C)110 ft
D)96 ft

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
52
Find the absolute maximum value and the absolute minimum value, if any, of the function. 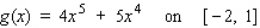
A)Absolute maximum value: 0; absolute minimum value: - 48
B)Absolute maximum value: 5; absolute minimum value: - 4
C)Absolute maximum value: 4; absolute minimum value: - 5
D)Absolute maximum value: 9; absolute minimum value: - 48
E)Absolute maximum value: 9; absolute minimum value: 0
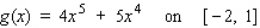
A)Absolute maximum value: 0; absolute minimum value: - 48
B)Absolute maximum value: 5; absolute minimum value: - 4
C)Absolute maximum value: 4; absolute minimum value: - 5
D)Absolute maximum value: 9; absolute minimum value: - 48
E)Absolute maximum value: 9; absolute minimum value: 0

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
53
The quantity demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, manufactured by Phonola Record Industries, is related to the price/compact disc. The equation 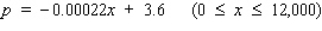 , where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
, where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by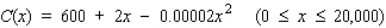 .
.
To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is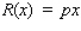 , and the profit is
, and the profit is 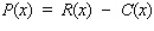 .
.
A)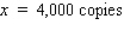
B)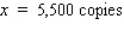
C)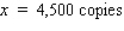
D)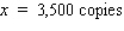
E)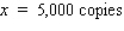
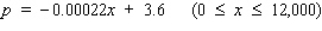 , where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
, where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by
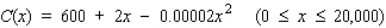 .
.To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is
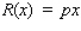 , and the profit is
, and the profit is 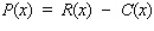 .
.A)
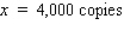
B)
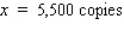
C)
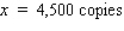
D)
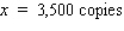
E)
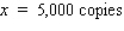

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
54
A manufacturer of tennis rackets finds that the total cost C(x) (in dollars) of manufacturing x rackets/day is given by 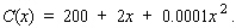 Each racket can be sold at a price of p dollars, where p is related to x by the demand equation
Each racket can be sold at a price of p dollars, where p is related to x by the demand equation 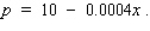 If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
A)6,000 rackets/day
B)11,000 rackets/day
C)7,000 rackets/day
D)8,000 rackets/day
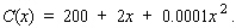 Each racket can be sold at a price of p dollars, where p is related to x by the demand equation
Each racket can be sold at a price of p dollars, where p is related to x by the demand equation 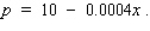 If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.A)6,000 rackets/day
B)11,000 rackets/day
C)7,000 rackets/day
D)8,000 rackets/day

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
55
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 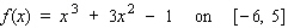
A)Absolute maximum value: 199; absolute minimum value: - 1
B)Absolute maximum value: 3; absolute minimum value: - 1
C)Absolute maximum value: 3; absolute minimum value: - 109
D)Absolute maximum value: 199; absolute minimum value: - 109
E)No absolute extrema
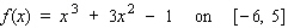
A)Absolute maximum value: 199; absolute minimum value: - 1
B)Absolute maximum value: 3; absolute minimum value: - 1
C)Absolute maximum value: 3; absolute minimum value: - 109
D)Absolute maximum value: 199; absolute minimum value: - 109
E)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
56
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 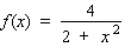
A)Absolute maximum value: 2; absolute minimum value: - 2
B)Absolute maximum value: 2; absolute minimum value: none
C)Absolute maximum value: 4; absolute minimum value: none
D)No absolute extrema
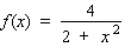
A)Absolute maximum value: 2; absolute minimum value: - 2
B)Absolute maximum value: 2; absolute minimum value: none
C)Absolute maximum value: 4; absolute minimum value: none
D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
57
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 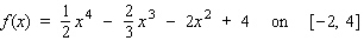
A)Absolute maximum value: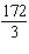 ; absolute minimum value:
; absolute minimum value:
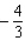
B)Absolute maximum value: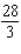 ; absolute minimum value:
; absolute minimum value:
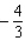
C)Absolute maximum value: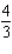 ; absolute minimum value:
; absolute minimum value:
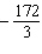
D)No absolute extrema
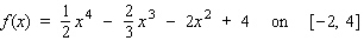
A)Absolute maximum value:
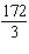 ; absolute minimum value:
; absolute minimum value: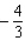
B)Absolute maximum value:
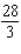 ; absolute minimum value:
; absolute minimum value: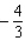
C)Absolute maximum value:
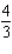 ; absolute minimum value:
; absolute minimum value: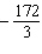
D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
58
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 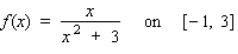
A)Absolute maximum value: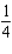 ; absolute minimum value:
; absolute minimum value:
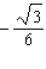
B)Absolute maximum value: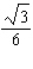 ; absolute minimum value:
; absolute minimum value:
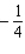
C)Absolute maximum value: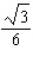 ; absolute minimum value:
; absolute minimum value:
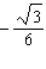
D)No absolute extrema
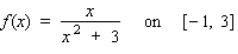
A)Absolute maximum value:
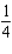 ; absolute minimum value:
; absolute minimum value: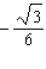
B)Absolute maximum value:
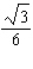 ; absolute minimum value:
; absolute minimum value: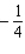
C)Absolute maximum value:
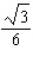 ; absolute minimum value:
; absolute minimum value: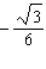
D)No absolute extrema

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
59
The estimated monthly profit (in dollars) realizable by Cannon Precision Instruments for manufacturing and selling x units of its model M1 camera is 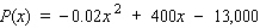 To maximize its profits, how many cameras should Cannon produce each month?
To maximize its profits, how many cameras should Cannon produce each month?
A)10,000 cameras
B)10,100 cameras
C)10,050 cameras
D)10,025 cameras
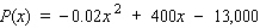 To maximize its profits, how many cameras should Cannon produce each month?
To maximize its profits, how many cameras should Cannon produce each month?A)10,000 cameras
B)10,100 cameras
C)10,050 cameras
D)10,025 cameras

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
60
Suppose the total cost function for manufacturing a certain product is 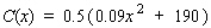 dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.
dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.
A)46 units
B)50 units
C)40 units
D)44 units
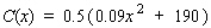 dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.
dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.A)46 units
B)50 units
C)40 units
D)44 units

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
61
The estimated monthly profit (in dollars) realizable by Cannon Precision Instruments for manufacturing and selling x units of its model M1 camera is 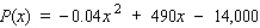 .
.
To maximize its profits, how many cameras should Cannon produce each month?
__________ cameras
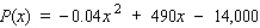 .
.To maximize its profits, how many cameras should Cannon produce each month?
__________ cameras

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
62
Find the horizontal and vertical asymptotes of the graph. 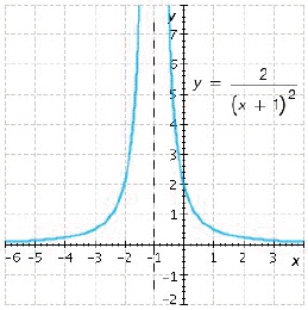
A)Horizontal asymptote is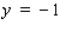 , vertical asymptote is
, vertical asymptote is
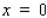
B)Horizontal asymptote is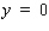 , vertical asymptote is
, vertical asymptote is
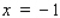
C)Horizontal asymptote is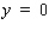 , vertical asymptote is
, vertical asymptote is
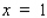
D)Horizontal asymptote is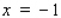 , vertical asymptote is
, vertical asymptote is
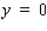
E)Horizontal asymptote is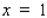 , vertical asymptote is
, vertical asymptote is
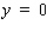

A)Horizontal asymptote is
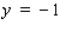 , vertical asymptote is
, vertical asymptote is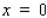
B)Horizontal asymptote is
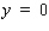 , vertical asymptote is
, vertical asymptote is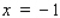
C)Horizontal asymptote is
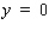 , vertical asymptote is
, vertical asymptote is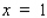
D)Horizontal asymptote is
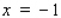 , vertical asymptote is
, vertical asymptote is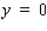
E)Horizontal asymptote is
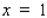 , vertical asymptote is
, vertical asymptote is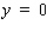

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
63
A stone is thrown straight up from the roof of an 60-ft building.The height (in feet) of the stone at any time t (in seconds), measured from the ground, is given by 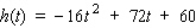 .
.
What is the maximum height the stone reaches?
__________ ft
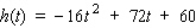 .
.What is the maximum height the stone reaches?
__________ ft

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
64
Find the horizontal and vertical asymptotes of the graph. 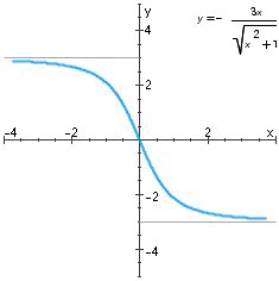
A)Horizontal asymptotes: y = 3 and y = - 3
B)Vertical asymptotes: x = 3 and x = -3
C)Horizontal asymptotes: y = 3 and y = - 3; Vertical asymptote: x = 0
D)Horizontal asymptote: y = 1; Vertical asymptote: y = 3

A)Horizontal asymptotes: y = 3 and y = - 3
B)Vertical asymptotes: x = 3 and x = -3
C)Horizontal asymptotes: y = 3 and y = - 3; Vertical asymptote: x = 0
D)Horizontal asymptote: y = 1; Vertical asymptote: y = 3

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
65
After the economy softened, the sky-high office space rents of the late 1990s started to come down to earth.The function R gives the approximate price per square foot in dollars, R(t), of prime space in Boston's Back Bay and Financial District from 1997 (  ) through 2000, where
) through 2000, where 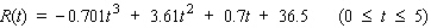 . What was the highest office space rent during the period in question? Hint: Use the quadratic formula.
. What was the highest office space rent during the period in question? Hint: Use the quadratic formula.
A)$53.02 per sq ft
B)$52.92 per sq ft
C)$52.97 per sq ft
D)$53.07 per sq ft
E)$53.12 per sq ft
 ) through 2000, where
) through 2000, where 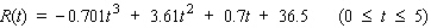 . What was the highest office space rent during the period in question? Hint: Use the quadratic formula.
. What was the highest office space rent during the period in question? Hint: Use the quadratic formula.A)$53.02 per sq ft
B)$52.92 per sq ft
C)$52.97 per sq ft
D)$53.07 per sq ft
E)$53.12 per sq ft

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
66
Find the horizontal and vertical asymptotes of the graph. 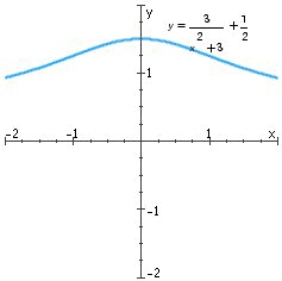
A)Horizontal asymptote: y = 0.5
B)Horizontal asymptote: y = 0.5; Vertical asymptote: x = 0
C)Horizontal asymptotes: y = 0.5 and y = 1.5
D)Vertical asymptote: x = 0

A)Horizontal asymptote: y = 0.5
B)Horizontal asymptote: y = 0.5; Vertical asymptote: x = 0
C)Horizontal asymptotes: y = 0.5 and y = 1.5
D)Vertical asymptote: x = 0

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose the quantity demanded per week of a certain dress is related to the unit price p by the demand equation 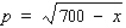 , where p is in dollars and x is the number of dresses made.
, where p is in dollars and x is the number of dresses made.
To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px.) Round the answer to the nearest integer.
__________ dresses
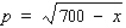 , where p is in dollars and x is the number of dresses made.
, where p is in dollars and x is the number of dresses made.To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px.) Round the answer to the nearest integer.
__________ dresses

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
68
If f is not continuous on the closed interval 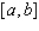 , then f cannot have an absolute maximum value.
, then f cannot have an absolute maximum value.
A)false
B)true
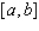 , then f cannot have an absolute maximum value.
, then f cannot have an absolute maximum value.A)false
B)true

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
69
A manufacturer of tennis rackets finds that the total cost C(x) (in dollars) of manufacturing x rackets/day is given by 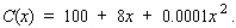 Each racket can be sold at a price of p dollars, where p is related to x by the demand equation
Each racket can be sold at a price of p dollars, where p is related to x by the demand equation 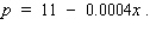 If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
__________ rackets/day
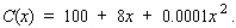 Each racket can be sold at a price of p dollars, where p is related to x by the demand equation
Each racket can be sold at a price of p dollars, where p is related to x by the demand equation 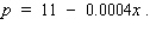 If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.__________ rackets/day

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
70
Answer true or false.
If f is defined on a closed interval , then f has an absolute maximum value.
, then f has an absolute maximum value.
If f is defined on a closed interval
 , then f has an absolute maximum value.
, then f has an absolute maximum value.
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
71
A division of Chapman Corporation manufactures a pager.The weekly fixed cost for the division is $20,000, and the variable cost for producing x pagers/week is 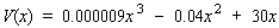 dollars.The company realizes a revenue of
dollars.The company realizes a revenue of 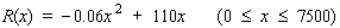 dollars from the sale of x pagers/week.
dollars from the sale of x pagers/week.
Find the level of production that will yield a maximum profit for the manufacturer.(Hint: Use the quadratic formula.)
__________ pagers/week
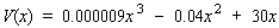 dollars.The company realizes a revenue of
dollars.The company realizes a revenue of 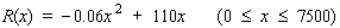 dollars from the sale of x pagers/week.
dollars from the sale of x pagers/week.Find the level of production that will yield a maximum profit for the manufacturer.(Hint: Use the quadratic formula.)
__________ pagers/week

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
72
Lynbrook West, an apartment complex, has 100 two-bedroom units.The monthly profit (in dollars) realized from renting out x apartments is given by 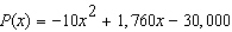 To maximize the monthly rental profit, how many units should be rented out? What is the maximum monthly profit realizable?
To maximize the monthly rental profit, how many units should be rented out? What is the maximum monthly profit realizable?
A)88 units are rented and the maximum monthly profit realizable is $23,720
B)22 units are rented and the maximum monthly profit realizable is $47,440
C)88 units are rented and the maximum monthly profit realizable ix $11,860
D)88 units are rented and the maximum monthly profit realizable is $47,440
E)44 units are rented and the maximum monthly profit realizable is $47,440
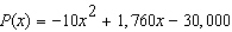 To maximize the monthly rental profit, how many units should be rented out? What is the maximum monthly profit realizable?
To maximize the monthly rental profit, how many units should be rented out? What is the maximum monthly profit realizable?A)88 units are rented and the maximum monthly profit realizable is $23,720
B)22 units are rented and the maximum monthly profit realizable is $47,440
C)88 units are rented and the maximum monthly profit realizable ix $11,860
D)88 units are rented and the maximum monthly profit realizable is $47,440
E)44 units are rented and the maximum monthly profit realizable is $47,440

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
73
The number of major crimes committed in the city of Bronxville between 1997 and 2004 is approximated by the function 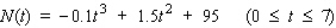 where N(t) denotes the number of crimes committed in year t (
where N(t) denotes the number of crimes committed in year t ( 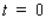 corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens of Bronxville with the help of the local police organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace. When was the growth in the crime rate maximal?
corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens of Bronxville with the help of the local police organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace. When was the growth in the crime rate maximal?
A)2000
B)2001
C)2002
D)1999
E)2003
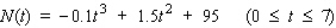 where N(t) denotes the number of crimes committed in year t (
where N(t) denotes the number of crimes committed in year t ( 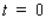 corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens of Bronxville with the help of the local police organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace. When was the growth in the crime rate maximal?
corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens of Bronxville with the help of the local police organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace. When was the growth in the crime rate maximal?A)2000
B)2001
C)2002
D)1999
E)2003

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
74
The average speed of a vehicle on a stretch of a route between 6
A.M.At what time of the morning commute is the traffic moving at the slowest rate? What is the average speed of a vehicle at that time?
time = __________
A.M.average speed = __________ mph
A.M.and 10
A.M.on a typical weekday is approximated by the function
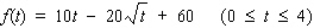 , where f (t) is measured in miles per hour and t is measured in hours, with t = 0 corresponding to 6
, where f (t) is measured in miles per hour and t is measured in hours, with t = 0 corresponding to 6
A.M.At what time of the morning commute is the traffic moving at the slowest rate? What is the average speed of a vehicle at that time?
time = __________
A.M.average speed = __________ mph
A.M.and 10
A.M.on a typical weekday is approximated by the function
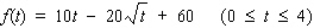 , where f (t) is measured in miles per hour and t is measured in hours, with t = 0 corresponding to 6
, where f (t) is measured in miles per hour and t is measured in hours, with t = 0 corresponding to 6
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
75
The quantity demanded each month of the Sicard wristwatch is related to the unit price by the equation 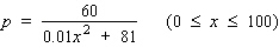 , where p is measured in dollars and x is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
, where p is measured in dollars and x is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
A)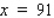
B)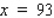
C)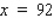
D)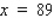
E)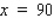
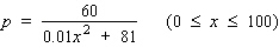 , where p is measured in dollars and x is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
, where p is measured in dollars and x is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?A)
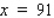
B)
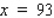
C)
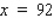
D)
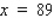
E)
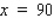

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
76
Find the horizontal and vertical asymptotes of the graph. 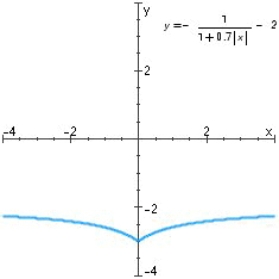
A)Horizontal asymptote: y = -2 ; vertical asymptote x = 0
B)Vertical asymptote: x = 0 .
C)Horizontal asymptotes: y = -2 and y = -3
D)Horizontal asymptote: y = -2

A)Horizontal asymptote: y = -2 ; vertical asymptote x = 0
B)Vertical asymptote: x = 0 .
C)Horizontal asymptotes: y = -2 and y = -3
D)Horizontal asymptote: y = -2

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
77
The number of major crimes committed in the city between 1997 and 2004 is approximated by the function 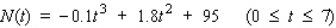 where N(t) denotes the number of crimes committed in year t (
where N(t) denotes the number of crimes committed in year t ( 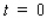 corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens, with the help of the local police, organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace.
corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens, with the help of the local police, organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace.
Show that the growth in the crime rate was maximal in 2003, giving credence to the claim that the Neighborhood Crime Watch program was working.
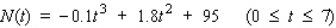 where N(t) denotes the number of crimes committed in year t (
where N(t) denotes the number of crimes committed in year t ( 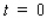 corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens, with the help of the local police, organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace.
corresponds to 1997).Enraged by the dramatic increase in the crime rate, the citizens, with the help of the local police, organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace.Show that the growth in the crime rate was maximal in 2003, giving credence to the claim that the Neighborhood Crime Watch program was working.

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
78
The quantity demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, manufactured by Phonola Record Industries, is related to the price/compact disc.The equation 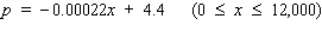 , where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
, where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by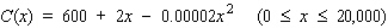 .
.
To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is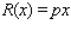 , and the profit is
, and the profit is 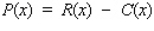 .
. 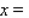 __________ copies
__________ copies
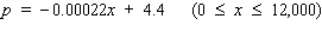 , where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
, where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by
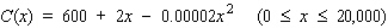 .
.To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is
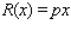 , and the profit is
, and the profit is 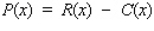 .
. 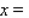 __________ copies
__________ copies
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
79
The quantity demanded each month of the Sicard wristwatch is related to the unit price by the equation 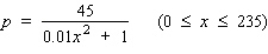 , where p is measured in dollars and x is measured in units of a thousand.
, where p is measured in dollars and x is measured in units of a thousand.
To yield a maximum revenue, how many watches must be sold?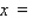 __________
__________
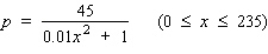 , where p is measured in dollars and x is measured in units of a thousand.
, where p is measured in dollars and x is measured in units of a thousand.To yield a maximum revenue, how many watches must be sold?
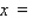 __________
__________
Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck
80
Suppose the total cost function for manufacturing a certain product is 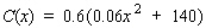 dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.
dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.
__________ units
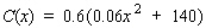 dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.
dollars, where x represents the number of units produced.Find the level of production that will minimize the average cost.Round the answer to the nearest integer.__________ units

Unlock Deck
Unlock for access to all 184 flashcards in this deck.
Unlock Deck
k this deck


