Deck 13: Experimental Design and Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 13: Experimental Design and Analysis of Variance
1
In an ANOVA procedure, a term that means the same as the term "variable" is
A) factor.
B) treatment.
C) replication.
D) within-variance.
A) factor.
B) treatment.
C) replication.
D) within-variance.
factor.
2
In an analysis of variance problem involving 3 treatments and 10 observations per treatment, SSE = 399.6. The MSE for this situation is
A) 133.2.
B) 33.32.
C) 12.1.
D) 11.1.
A) 133.2.
B) 33.32.
C) 12.1.
D) 11.1.
12.1.
3
The mean square is the sum of squares divided by
A) the total number of observations.
B) its corresponding degrees of freedom.
C) its corresponding degrees of freedom minus one.
D) the total number of replications.
A) the total number of observations.
B) its corresponding degrees of freedom.
C) its corresponding degrees of freedom minus one.
D) the total number of replications.
its corresponding degrees of freedom.
4
The ANOVA procedure is a statistical approach for determining whether or not the means of _____ are equal.
A) two samples
B) two or more samples
C) two populations
D) three or more populations
A) two samples
B) two or more samples
C) two populations
D) three or more populations

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
An ANOVA procedure is applied to data obtained from 6 samples where each sample contains 20 observations. The critical value of F occurs with
A) 6 numerator and 20 denominator degrees of freedom.
B) 5 numerator and 20 denominator degrees of freedom.
C) 5 numerator and 114 denominator degrees of freedom.
D) 6 numerator and 114 denominator degrees of freedom.
A) 6 numerator and 20 denominator degrees of freedom.
B) 5 numerator and 20 denominator degrees of freedom.
C) 5 numerator and 114 denominator degrees of freedom.
D) 6 numerator and 114 denominator degrees of freedom.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
The number of times each experimental condition is observed in a factorial design is known as
A) partition.
B) replication.
C) blocking.
D) factor.
A) partition.
B) replication.
C) blocking.
D) factor.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
In the analysis of variance procedure (ANOVA), "factor" refers to
A) the dependent variable.
B) the independent variable.
C) different levels of a treatment.
D) the critical value of F.
A) the dependent variable.
B) the independent variable.
C) different levels of a treatment.
D) the critical value of F.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
The critical F value with 6 numerator and 40 denominator degrees of freedom at α = .05 is
A) 3.77.
B) 2.25.
C) 2.34.
D) 1.96.
A) 3.77.
B) 2.25.
C) 2.34.
D) 1.96.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
The independent variable of interest in an ANOVA procedure is called a
A) partition.
B) treatment.
C) response.
D) factor.
A) partition.
B) treatment.
C) response.
D) factor.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
In order to determine whether or not the means of two populations are equal,
A) a t test must be performed.
B) an analysis of variance must be performed.
C) either a t test or an analysis of variance can be performed.
D) a chi-square test can be performed.
A) a t test must be performed.
B) an analysis of variance must be performed.
C) either a t test or an analysis of variance can be performed.
D) a chi-square test can be performed.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
In an analysis of variance where the total sample size for the experiment is nT and the number of populations is k, the mean square due to error is
A) SSE/(nT - k).
B) SSTR/(nT - k).
C) SSE/(k - 1).
D) SSTR/k.
A) SSE/(nT - k).
B) SSTR/(nT - k).
C) SSE/(k - 1).
D) SSTR/k.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
When an analysis of variance is performed on samples drawn from k populations, the mean square due to treatments (MSTR) is
A) SSTR/nT.
B) SSTR/(nT - 1).
C) SSTR/k.
D) SSTR/(k - 1).
A) SSTR/nT.
B) SSTR/(nT - 1).
C) SSTR/k.
D) SSTR/(k - 1).

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
The F ratio in a completely randomized ANOVA is given by
A) MSTR/MSE.
B) MST/MSE.
C) MSE/MSTR.
D) MSE/MST.
A) MSTR/MSE.
B) MST/MSE.
C) MSE/MSTR.
D) MSE/MST.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
In ANOVA, which of the following is not affected by whether or not the population means are equal?
A)
B) between-treatments estimate of σ2
C) within-treatments estimate of σ2
D) ratio of between- and within-treatments estimate of σ2
A)

B) between-treatments estimate of σ2
C) within-treatments estimate of σ2
D) ratio of between- and within-treatments estimate of σ2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
In factorial designs, the response produced when the treatments of one factor interact with the treatments of another in influencing the response variable is known as
A) main effect.
B) replication.
C) interaction.
D) error.
A) main effect.
B) replication.
C) interaction.
D) error.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
The required condition for using an ANOVA procedure on data from several populations is that the
A) selected samples are dependent on each other.
B) response variables from samples are all uniform.
C) sampled populations have equal variances.
D) sampled populations have equal means.
A) selected samples are dependent on each other.
B) response variables from samples are all uniform.
C) sampled populations have equal variances.
D) sampled populations have equal means.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
An experimental design where the experimental units are randomly assigned to the treatments is known as _____ design.
A) factor block
B) random factor
C) completely randomized
D) randomized treatment
A) factor block
B) random factor
C) completely randomized
D) randomized treatment

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
In an analysis of variance problem if SST = 120 and SSTR = 90, then SSE is
A) 210.
B) 30.
C) 80.
D) 120.
A) 210.
B) 30.
C) 80.
D) 120.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
An ANOVA procedure is used for data that was obtained from five sample groups each comprised of six observations. The degrees of freedom for the critical value of F are
A) 5 and 30.
B) 4 and 25.
C) 4 and 30.
D) 4 and 6.
A) 5 and 30.
B) 4 and 25.
C) 4 and 30.
D) 4 and 6.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
In the ANOVA, treatments refer to
A) experimental units.
B) different levels of a factor.
C) the dependent variables.
D) statistical applications.
A) experimental units.
B) different levels of a factor.
C) the dependent variables.
D) statistical applications.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
In a completely randomized design involving four treatments, the following information is provided. 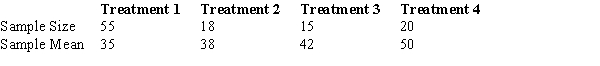 The overall mean (the grand mean) for all treatments is
The overall mean (the grand mean) for all treatments is
A) 40.0.
B) 40.76.
C) 39.25.
D) 41.25.
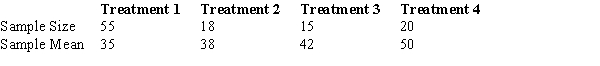 The overall mean (the grand mean) for all treatments is
The overall mean (the grand mean) for all treatments isA) 40.0.
B) 40.76.
C) 39.25.
D) 41.25.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
An ANOVA procedure is used for data obtained from five populations. Five samples, each comprised of 25 observations, were taken from the five populations. The numerator and denominator (respectively) degrees of freedom for the critical value of F are
A) 5 and 25.
B) 4 and 25.
C) 4 and 124.
D) 4 and 120.
A) 5 and 25.
B) 4 and 25.
C) 4 and 124.
D) 4 and 120.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following information.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 =μ5
SSE = 8000
Ha: At least one mean is different
The null hypothesis is to be tested at the 5% level of significance. The null hypothesis
A) should be rejected.
B) should not be rejected.
C) was designed incorrectly.
D) cannot be tested.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 =μ5
SSE = 8000
Ha: At least one mean is different
The null hypothesis is to be tested at the 5% level of significance. The null hypothesis
A) should be rejected.
B) should not be rejected.
C) was designed incorrectly.
D) cannot be tested.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the following ANOVA table. 
The mean square due to treatments equals
A) 288.
B) 518.4.
C) 1200.
D) 8294.4.

The mean square due to treatments equals
A) 288.
B) 518.4.
C) 1200.
D) 8294.4.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
An experimental design that permits simultaneous statistical conclusions about two or more factors is a
A) randomized block design.
B) factorial design.
C) completely randomized design.
D) multiple block design.
A) randomized block design.
B) factorial design.
C) completely randomized design.
D) multiple block design.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
The process of allocating the total sum of squares and degrees of freedom to the various components is called
A) factoring.
B) blocking.
C) replicating.
D) partitioning.
A) factoring.
B) blocking.
C) replicating.
D) partitioning.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
The critical F value with 8 numerator and 29 denominator degrees of freedom at α = .05 is
A) 2.28.
B) 3.20.
C) 3.33.
D) 3.64.
A) 2.28.
B) 3.20.
C) 3.33.
D) 3.64.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the following information. 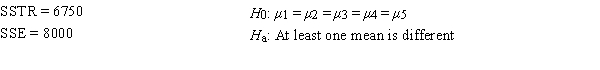
If n = 5, the mean square due to error (MSE) equals
A) 400.
B) 500.
C) 1687.5.
D) 2250.
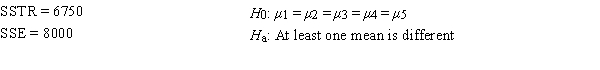
If n = 5, the mean square due to error (MSE) equals
A) 400.
B) 500.
C) 1687.5.
D) 2250.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the following ANOVA table. 
The sum of squares due to error equals
A) 13833.6.
B) 2073.6.
C) 5760.
D) 6000.

The sum of squares due to error equals
A) 13833.6.
B) 2073.6.
C) 5760.
D) 6000.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the following information.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 = μ5
SSE = 8000
Ha: At least one mean is different
The null hypothesis is to be tested at the 5% level of significance. The p-value is
A) less than .01.
B) between .01 and .025.
C) between .025 and .05.
D) greater than .10.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 = μ5
SSE = 8000
Ha: At least one mean is different
The null hypothesis is to be tested at the 5% level of significance. The p-value is
A) less than .01.
B) between .01 and .025.
C) between .025 and .05.
D) greater than .10.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
In an analysis of variance, one estimate of σ2 is based upon the differences between the treatment means and the
A) means of each sample.
B) overall sample mean.
C) sum of observations.
D) population means.
A) means of each sample.
B) overall sample mean.
C) sum of observations.
D) population means.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
An ANOVA procedure is used for data obtained from four populations. Four samples, each comprised of 25 observations, were taken from the four populations. The numerator and denominator (respectively) degrees of freedom for the critical value of F are
A) 3 and 25.
B) 4 and 25.
C) 3 and 99.
D) 3 and 96.
A) 3 and 25.
B) 4 and 25.
C) 3 and 99.
D) 3 and 96.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the following ANOVA table. 
The null hypothesis is to be tested at the 1% level of significance. The null hypothesis should
A) be rejected.
B) not be rejected.
C) be revised.
D) not be tested.

The null hypothesis is to be tested at the 1% level of significance. The null hypothesis should
A) be rejected.
B) not be rejected.
C) be revised.
D) not be tested.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the following ANOVA table. 
The null hypothesis for this ANOVA problem is
A) μ1 = μ2 = μ3 = μ4.
B) μ1 = μ2 = μ3 = μ4 = μ5.
C) μ1 = μ2 = μ3 = μ4 = μ5 = μ6.
D) μ1 = μ2 = ... = μ20.

The null hypothesis for this ANOVA problem is
A) μ1 = μ2 = μ3 = μ4.
B) μ1 = μ2 = μ3 = μ4 = μ5.
C) μ1 = μ2 = μ3 = μ4 = μ5 = μ6.
D) μ1 = μ2 = ... = μ20.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the following ANOVA table. 
The null hypothesis is to be tested at the 1% level of significance. The p-value is
A) greater than .10.
B) between .05 to .10.
C) between .025 to .05.
D) less than .01.

The null hypothesis is to be tested at the 1% level of significance. The p-value is
A) greater than .10.
B) between .05 to .10.
C) between .025 to .05.
D) less than .01.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the following ANOVA table. 
The test statistic to test the null hypothesis equals
A) .432.
B) 1.8.
C) 4.17.
D) 28.8.

The test statistic to test the null hypothesis equals
A) .432.
B) 1.8.
C) 4.17.
D) 28.8.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the following information.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 = μ5
SSE = 8000
Ha: At least one mean is different
The test statistic to test the null hypothesis equals
A) .22.
B) .84.
C) 4.22.
D) 4.50.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 = μ5
SSE = 8000
Ha: At least one mean is different
The test statistic to test the null hypothesis equals
A) .22.
B) .84.
C) 4.22.
D) 4.50.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the following information.
SSTR = 6750
H0: μ1 =μ2 =μ3 =μ4 = μ5
SSE = 8000
Ha: At least one mean is different
The mean square due to treatments (MSTR) equals
A) 400.
B) 500.
C) 1687.5.
D) 1350.
SSTR = 6750
H0: μ1 =μ2 =μ3 =μ4 = μ5
SSE = 8000
Ha: At least one mean is different
The mean square due to treatments (MSTR) equals
A) 400.
B) 500.
C) 1687.5.
D) 1350.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following is not a required assumption for the analysis of variance?
A) The random variable of interest for each population has a normal probability distribution.
B) The variance associated with the random variable must be the same for all populations.
C) At least 2 populations are under consideration.
D) Populations under consideration have equal means.
A) The random variable of interest for each population has a normal probability distribution.
B) The variance associated with the random variable must be the same for all populations.
C) At least 2 populations are under consideration.
D) Populations under consideration have equal means.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
In a completely randomized design involving three treatments, the following information is provided: 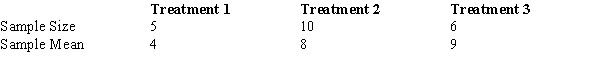 The overall mean (the grand mean) for all the treatments is
The overall mean (the grand mean) for all the treatments is
A) 7.33.
B) 7.00.
C) 7.25.
D) 8.55.
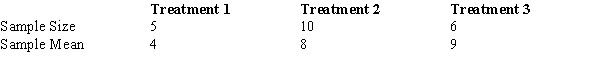 The overall mean (the grand mean) for all the treatments is
The overall mean (the grand mean) for all the treatments isA) 7.33.
B) 7.00.
C) 7.25.
D) 8.55.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 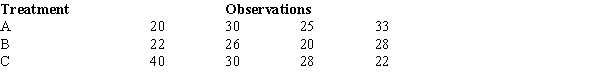
The null hypothesis is to be tested at the 1% level of significance. The null hypothesis
A) should be rejected.
B) should not be rejected.
C) should be revised.
D) should not be tested.
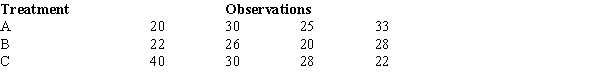
The null hypothesis is to be tested at the 1% level of significance. The null hypothesis
A) should be rejected.
B) should not be rejected.
C) should be revised.
D) should not be tested.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
Part of an ANOVA table is shown below.  The mean square due to treatments (MSTR) is
The mean square due to treatments (MSTR) is
A) 36.
B) 16.
C) 64.
D) 15.
 The mean square due to treatments (MSTR) is
The mean square due to treatments (MSTR) isA) 36.
B) 16.
C) 64.
D) 15.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
Part of an ANOVA table is shown below.  The number of degrees of freedom corresponding to between-treatments is
The number of degrees of freedom corresponding to between-treatments is
A) 18.
B) 2.
C) 4.
D) 3.
 The number of degrees of freedom corresponding to between-treatments is
The number of degrees of freedom corresponding to between-treatments isA) 18.
B) 2.
C) 4.
D) 3.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to within-treatments is
A) 60.
B) 59.
C) 5.
D) 4.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to within-treatments is
A) 60.
B) 59.
C) 5.
D) 4.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 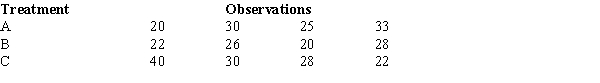
The mean square due to treatments (MSTR) equals
A) 1.872.
B) 5.86.
C) 34.
D) 36.
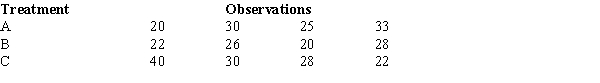
The mean square due to treatments (MSTR) equals
A) 1.872.
B) 5.86.
C) 34.
D) 36.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 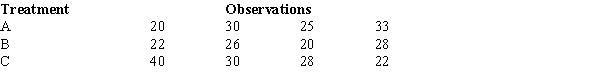
The test statistic to test the null hypothesis equals
A) .944.
B) 1.06.
C) 3.13.
D) 19.231.
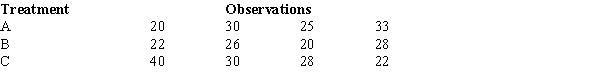
The test statistic to test the null hypothesis equals
A) .944.
B) 1.06.
C) 3.13.
D) 19.231.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The mean square due to treatments (MSTR) is
A) 60.00.
B) 10.00.
C) 75.00.
D) 12.00.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The mean square due to treatments (MSTR) is
A) 60.00.
B) 10.00.
C) 75.00.
D) 12.00.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to between-treatments is
A) 60.
B) 59.
C) 5.
D) 4.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to between-treatments is
A) 60.
B) 59.
C) 5.
D) 4.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
Part of an ANOVA table is shown below.  The mean square due to treatments (MSTR) is
The mean square due to treatments (MSTR) is
A) 20.
B) 60.
C) 18.
D) 15.
 The mean square due to treatments (MSTR) is
The mean square due to treatments (MSTR) isA) 20.
B) 60.
C) 18.
D) 15.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The mean square due to error (MSE) is
A) 75.
B) 8.3.
C) 200.
D) 500.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The mean square due to error (MSE) is
A) 75.
B) 8.3.
C) 200.
D) 500.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
Part of an ANOVA table is shown below.  The test statistic is
The test statistic is
A) 2.25.
B) 6.00.
C) 2.67.
D) 3.00.
 The test statistic is
The test statistic isA) 2.25.
B) 6.00.
C) 2.67.
D) 3.00.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
Part of an ANOVA table is shown below.  The mean square due to error (MSE) is
The mean square due to error (MSE) is
A) 60.
B) 15.
C) 18.
D) 20.
 The mean square due to error (MSE) is
The mean square due to error (MSE) isA) 60.
B) 15.
C) 18.
D) 20.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
If, at a 5% level of significance, we want to determine whether or not the means of the five populations are equal, the critical value of F is
A) 2.53.
B) 19.48.
C) 4.98.
D) 5.69.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
If, at a 5% level of significance, we want to determine whether or not the means of the five populations are equal, the critical value of F is
A) 2.53.
B) 19.48.
C) 4.98.
D) 5.69.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). The following information is provided.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
If we want to determine whether or not the means of the five populations are equal, the p-value is
A) greater than .10.
B) between .025 to .05.
C) between .01 to .025.
D) less than .01.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
If we want to determine whether or not the means of the five populations are equal, the p-value is
A) greater than .10.
B) between .025 to .05.
C) between .01 to .025.
D) less than .01.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 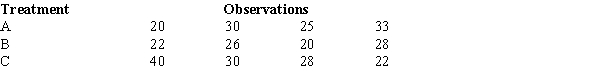
The null hypothesis for this ANOVA problem is
A) μ1 = μ2.
B) μ1 = μ2 = μ3.
C) μ1 = μ2 = μ3 = μ4.
D) μ1 = μ2 = ... = μ12.
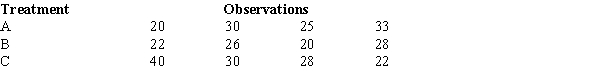
The null hypothesis for this ANOVA problem is
A) μ1 = μ2.
B) μ1 = μ2 = μ3.
C) μ1 = μ2 = μ3 = μ4.
D) μ1 = μ2 = ... = μ12.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). The following information is provided.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The test statistic is
A) .11.
B) 9.04.
C) 3.75.
D) 15.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The test statistic is
A) .11.
B) 9.04.
C) 3.75.
D) 15.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 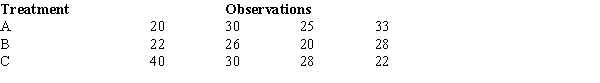 The mean square due to error (MSE) equals
The mean square due to error (MSE) equals
A) 1.872.
B) 5.86.
C) 34.
D) 36.
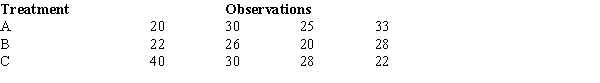 The mean square due to error (MSE) equals
The mean square due to error (MSE) equalsA) 1.872.
B) 5.86.
C) 34.
D) 36.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 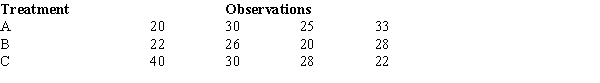
The null hypothesis is to be tested at the 1% level of significance. The p-value is
A) greater than .1.
B) between .05 to .10.
C) less than .01.
D) between .01 to .025.
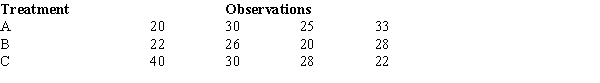
The null hypothesis is to be tested at the 1% level of significance. The p-value is
A) greater than .1.
B) between .05 to .10.
C) less than .01.
D) between .01 to .025.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
Part of an ANOVA table is shown below.  The number of degrees of freedom corresponding to within-treatments is
The number of degrees of freedom corresponding to within-treatments is
A) 22.
B) 4.
C) 5.
D) 18.
 The number of degrees of freedom corresponding to within-treatments is
The number of degrees of freedom corresponding to within-treatments isA) 22.
B) 4.
C) 5.
D) 18.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The sum of squares due to error (SSE) is
A) 1100.
B) 500.
C) 300.
D) 1600.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The sum of squares due to error (SSE) is
A) 1100.
B) 500.
C) 300.
D) 1600.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
The heating bills for a selected sample of houses in a city using various forms of heating are given below (values are in dollars). 
At α = .05, test to see if there is a significant difference among the average bills of all the homes (in a city) using three forms of heating. Use both the critical and p-value approaches.

At α = .05, test to see if there is a significant difference among the average bills of all the homes (in a city) using three forms of heating. Use both the critical and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
Three universities in your state decided to administer the same comprehensive examination to the recipients of MBA degrees from the three institutions. From each institution, MBA recipients were randomly selected and were given the test. The following table shows the scores of the students tested by each university. 
At α = .01, test to see if there is any significant difference in the average scores of all the students who took the exam from the three universities. (Note that the sample sizes are not equal.) Use both the critical and p-value approaches.

At α = .01, test to see if there is any significant difference in the average scores of all the students who took the exam from the three universities. (Note that the sample sizes are not equal.) Use both the critical and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Individuals were randomly assigned to three different production processes. The hourly units of production for the three processes are shown below. 
Use the analysis of variance procedure with α = .05 to determine if there is a significant difference in the mean hourly units of production for the three types of production processes. Use both the critical and p-value approaches.

Use the analysis of variance procedure with α = .05 to determine if there is a significant difference in the mean hourly units of production for the three types of production processes. Use both the critical and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
At α = .01, test to determine if the means of the three populations (from which the following samples are selected) are equal. Use both the critical and p-value approaches. 


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
In testing for the equality of k population means, the number of treatments is
A) k.
B) k - 1.
C) nT.
D) nT - k.
A) k.
B) k - 1.
C) nT.
D) nT - k.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
In a factorial experiment, if there are x levels of factor A and y levels of factor B, there is a total of
A) x + y treatment combinations.
B) (x + y)/2 treatment combinations.
C) 2(x + y) treatment combinations.
D) xy treatment combinations.
A) x + y treatment combinations.
B) (x + y)/2 treatment combinations.
C) 2(x + y) treatment combinations.
D) xy treatment combinations.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
MNM, Inc. has three stores located in three different areas. Random samples of the daily sales of the three stores (in $1000) are shown below. 
At the 1% level of significance, test to see if there is a significant difference in the average sales of the three stores. Use both the critical and p-value approaches.

At the 1% level of significance, test to see if there is a significant difference in the average sales of the three stores. Use both the critical and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
For four populations, the population variances are assumed to be equal. Random samples from each population provide the following data. 
Using a .05 level of significance, test to see if the means for all four populations are the same.

Using a .05 level of significance, test to see if the means for all four populations are the same.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
A completely randomized design is useful when the experimental units are
A) homogeneous.
B) heterogeneous.
C) clustered.
D) stratified.
A) homogeneous.
B) heterogeneous.
C) clustered.
D) stratified.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
If we are testing for the equality of three population means, we should use the
A) test statistic t.
B) test statistic z.
C) test statistic F.
D) test statistic χ2.
A) test statistic t.
B) test statistic z.
C) test statistic F.
D) test statistic χ2.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
Random samples of employees from three different departments of MNM Corporation showed the following yearly incomes (in $1000). 
At α = .05, test to determine if there is a significant difference among the average incomes of the employees from the three departments. Use both the critical and p-value approaches.

At α = .05, test to determine if there is a significant difference among the average incomes of the employees from the three departments. Use both the critical and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
The test scores for selected samples of sociology students who took the course from three different instructors are shown below. 
At α = .05, test to see if there is a significant difference among the averages of the three groups. Use both the critical value and p-value approaches.

At α = .05, test to see if there is a significant difference among the averages of the three groups. Use both the critical value and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
Three major automobile manufacturers have entered their cars in the Indianapolis 500 race. The speeds (in miles per hour) of the tested cars are given below. Please note the sample sizes are not equal. 
At α = .05, test to see if there is a significant difference in the average racing speeds of the cars of the three auto manufacturers. Use both the critical and p-value approaches.

At α = .05, test to see if there is a significant difference in the average racing speeds of the cars of the three auto manufacturers. Use both the critical and p-value approaches.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
The process of using the same or similar experimental units for all treatments is called
A) factoring.
B) blocking.
C) replicating.
D) partitioning.
A) factoring.
B) blocking.
C) replicating.
D) partitioning.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Part of an ANOVA table is shown below.  If we want to determine whether or not the means of the populations are equal, the p-value is
If we want to determine whether or not the means of the populations are equal, the p-value is
A) greater than .1.
B) between .05 to .1.
C) between .025 to .05.
D) less than .01.
 If we want to determine whether or not the means of the populations are equal, the p-value is
If we want to determine whether or not the means of the populations are equal, the p-value isA) greater than .1.
B) between .05 to .1.
C) between .025 to .05.
D) less than .01.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Part of an ANOVA table is shown below.  At a 5% level of significance, if we want to determine whether or not the means of the populations are equal, the conclusion of the test is that
At a 5% level of significance, if we want to determine whether or not the means of the populations are equal, the conclusion of the test is that
A) all means are equal.
B) some means may be equal.
C) not all means are equal.
D) some means will never be equal.
 At a 5% level of significance, if we want to determine whether or not the means of the populations are equal, the conclusion of the test is that
At a 5% level of significance, if we want to determine whether or not the means of the populations are equal, the conclusion of the test is thatA) all means are equal.
B) some means may be equal.
C) not all means are equal.
D) some means will never be equal.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


