Deck 8: Rotational Motion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/130
Play
Full screen (f)
Deck 8: Rotational Motion
1
A particle moves uniformly around the circumference of a circle whose radius is 8.0 cm with a period of /20 s. The angular velocity of the particle is
A) 2.5 rad/s.
B) 3.2 102 rad/s.
C) 40 rad/s.
D) 7.9 rad/s.
E) 0.96 rad/s.
A) 2.5 rad/s.
B) 3.2 102 rad/s.
C) 40 rad/s.
D) 7.9 rad/s.
E) 0.96 rad/s.
40 rad/s.
2
Two objects, m1 and m2, both of mass m, are place on a horizontal platform that is rotating at a constant angular velocity. m1 = m is located at a distance R from the axis of rotation and the second object of mass m2 = 2m is located at a distance 2R. The angular velocity of mass m1____ to the angular velocity of m2.
A) is less than
B) is equal to
C) is greater than
D) depends how fast it is rotating
E) Unable to tell.
A) is less than
B) is equal to
C) is greater than
D) depends how fast it is rotating
E) Unable to tell.
is equal to
3
Four 50-g point masses are at the corners of a square with 20-cm sides. What is the moment of inertia of this system about an axis perpendicular to the plane of the square and passing through its center?
A) 1.0 10-3 kg · m2
B) 4.0 10-3 kg · m2
C) 2.0 10-3 kg · m2
D) 8.0 10-3 kg · m2
E) 2.8 10-3 kg · m2
A) 1.0 10-3 kg · m2
B) 4.0 10-3 kg · m2
C) 2.0 10-3 kg · m2
D) 8.0 10-3 kg · m2
E) 2.8 10-3 kg · m2
4.0 10-3 kg · m2
4
Two objects, m1 and m2, both of mass m, are placed on a horizontal platform that is rotating at a constant angular velocity. m1 is located at a distance R from the axis of rotation and m2 is located at a R. The centripetal acceleration of mass m1 ____ to the centripetal acceleration of m2.
A) is less than
B) is equal to
C) is greater than
D) depends how fast it is rotating
E) Unable to tell.
A) is less than
B) is equal to
C) is greater than
D) depends how fast it is rotating
E) Unable to tell.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
5
A hoop of mass 50 kg rolls without slipping. If the center of mass of the hoop has a translational speed of 4.0 m/s, the total kinetic energy of the hoop is
A) 0.20 kJ.
B) 0.40 kJ.
C) 1.1 kJ.
D) 3.9 kJ.
E) None of these is correct.
A) 0.20 kJ.
B) 0.40 kJ.
C) 1.1 kJ.
D) 3.9 kJ.
E) None of these is correct.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
6
You have a friend who lives in the southern part of the United States, and you live in the northern part. As Earth rotates, your linear velocity is ___________ hers, and your angular velocity is ____________ hers.
A) greater than; equal to
B) equal to; greater than
C) greater than; less than
D) less than; greater than
E) less than; equal to
A) greater than; equal to
B) equal to; greater than
C) greater than; less than
D) less than; greater than
E) less than; equal to

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
7
The moment of inertia of a slim rod about a transverse crosswise) axis through one end is mL2/3, where m is the mass of the rod and L is its length. The moment of inertia of a 0.24-kg meter stick about a transverse axis through its center is
A) 0.14 kg · m2.
B) 20 kg · m2.
C) 0.020 kg · m2.
D) 80 kg · m2.
E) 4.5 kg · m2.
A) 0.14 kg · m2.
B) 20 kg · m2.
C) 0.020 kg · m2.
D) 80 kg · m2.
E) 4.5 kg · m2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
8
A hoop of radius 3.05 m has a mass of 145 kg. Its moment of inertia is mR2. The hoop rolls without slipping along a horizontal plane. If the center of mass of the hoop has a speed of 0.305 m/s, the work required to bring the hoop to rest is
A) 6.78 J.
B) 13.5 J.
C) 682 J.
D) 217 J.
E) 4.34 kJ.
A) 6.78 J.
B) 13.5 J.
C) 682 J.
D) 217 J.
E) 4.34 kJ.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
9
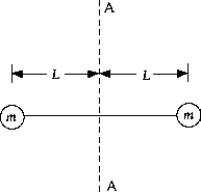 The moment of inertia of a set of dumbbells, considered as two mass points m separated by a distance 2L about the axis A, is
The moment of inertia of a set of dumbbells, considered as two mass points m separated by a distance 2L about the axis A, isA) mL2.
B)
 mL2.
mL2. C) 2mL2.
D)
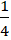 mL2.
mL2. E) 4mL2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
10
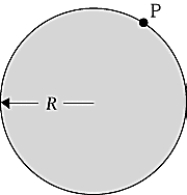 A homogeneous solid cylinder of mass m, length L, and radius R rotates about an axis through point P, which is parallel to the cylinder axis. If the moment of inertia about the cylinder axis is
A homogeneous solid cylinder of mass m, length L, and radius R rotates about an axis through point P, which is parallel to the cylinder axis. If the moment of inertia about the cylinder axis is  mR2, the moment of inertia about the axis through P is
mR2, the moment of inertia about the axis through P isA) 0.4mR2.
B) 11ec81b0_c290_3328_8138_9d3307bc9410_TB7291_11mR2.
C) 2/3 mR2.
D) mR2.
E) 1.5mR2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
11
A wheel on a car is rolling without slipping along level ground. The speed of the car is 36 m/s. The wheel has an outer diameter of 50 cm. The speed of the top of the wheel is
A) 36 m/s.
B) 3.6 m/s.
C) 72 m/s.
D) 18 m/s.
E) 98 m/s.
A) 36 m/s.
B) 3.6 m/s.
C) 72 m/s.
D) 18 m/s.
E) 98 m/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
12
The London Eye, a giant Ferris wheel, has a diameter of 135 m. It revolves at a constant rate and takes 30 minutes to complete one revolution. What is the linear velocity of a rider in a capsule that is located at the perimeter of the wheel?
A) 0.24 m/s
B) 0.47 m/s
C) 3.5 m/s
D) 7.1 m/s
E) None of the above.
A) 0.24 m/s
B) 0.47 m/s
C) 3.5 m/s
D) 7.1 m/s
E) None of the above.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
13
The moment of inertia of a slim rod of mass m and length L about a transverse axis through one end is mL2/3. The moment of inertia of such a rod about a transverse axis through the rod at a distance L/3 from one end is
A) mL2/36.
B) 7mL2/36.
C) mL2/9.
D) 2mL2/9.
E) 4mL2/9.
A) mL2/36.
B) 7mL2/36.
C) mL2/9.
D) 2mL2/9.
E) 4mL2/9.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
14
A wheel of radius R is rolling without slipping. The velocity of the point on the rim that is in contact with the surface, relative to the surface, is
A) equal to R in the direction of motion of the center of mass.
B) equal to R opposite the direction of motion of the center of mass.
C) zero.
D) equal to the velocity of the center of mass and in the same direction.
E) equal to the velocity of the center of mass but in the opposite direction.
A) equal to R in the direction of motion of the center of mass.
B) equal to R opposite the direction of motion of the center of mass.
C) zero.
D) equal to the velocity of the center of mass and in the same direction.
E) equal to the velocity of the center of mass but in the opposite direction.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
15
A wheel is rotating at 30 rev/min. The angular velocity of the wheel is
A) 2π2 rad/s.
B) 2π rad/s.
C) 2 rad/s.
D) π/2 rad/s.
E) π rad/s.
A) 2π2 rad/s.
B) 2π rad/s.
C) 2 rad/s.
D) π/2 rad/s.
E) π rad/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
16
To increase the moment of inertia of a body about an axis, you must
A) increase the angular acceleration.
B) increase the angular velocity.
C) decrease the angular velocity.
D) make the body occupy less space.
E) place part of the body farther from the axis.
A) increase the angular acceleration.
B) increase the angular velocity.
C) decrease the angular velocity.
D) make the body occupy less space.
E) place part of the body farther from the axis.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
17
The disc brake of a high performance car is often made of carbon fiber instead of iron, thereby reducing the mass. If the mass of a carbon disc is that of iron for the same shape and size, by what factor is the moment of inertia changed?
A) one quarter
B) half
C) unchanged
D) doubled
E) quadrupled
A) one quarter
B) half
C) unchanged
D) doubled
E) quadrupled

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
18
A particle is moving uniformly in a circle of radius 50 cm. Its angular velocity is 96 rad/s. The linear speed of the particle is
A) 1.0 m/s.
B) 96 cm/s.
C) 48 m/s.
D) zero.
E) 15 m/s.
A) 1.0 m/s.
B) 96 cm/s.
C) 48 m/s.
D) zero.
E) 15 m/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
19
A body of mass m is whirled at a constant angular velocity on the end of a string of length R. To double the kinetic energy of the body as it whirls while maintaining the angular velocity, the length of the string must be changed to
A) 2R.
B)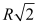 .
.
C) R/2.
D) 4R.
E)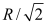 .
.
A) 2R.
B)
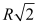 .
.C) R/2.
D) 4R.
E)
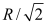 .
.
Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
20
Michelle Kwan, the American figure skater, is spinning on ice with her arms extended. She then draws her arms in and crosses them in front of her chest. How has her moment of inertia changed?
A) Her moment of inertia has decreased.
B) Her moment of inertia has increased.
C) Her moment of inertia has not changed.
D) Her moment of inertia decreases as she draws her arms in, but then returns to the initial value once she has crossed them.
E) Her moment of inertia increases as she draws her arms in, but then returns to the initial value once she has crossed them.
A) Her moment of inertia has decreased.
B) Her moment of inertia has increased.
C) Her moment of inertia has not changed.
D) Her moment of inertia decreases as she draws her arms in, but then returns to the initial value once she has crossed them.
E) Her moment of inertia increases as she draws her arms in, but then returns to the initial value once she has crossed them.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
21
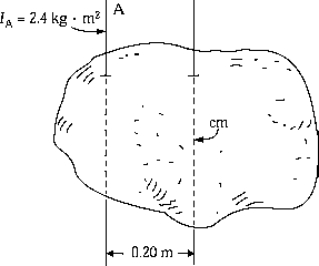 A stone of mass 10 kg has a rotational inertia of 2.4 kg · m2 about an axis A parallel to an axis through the center of mass. If axis A is 0.20 m from the center of mass axis, the rotational inertia about the center of mass axis is
A stone of mass 10 kg has a rotational inertia of 2.4 kg · m2 about an axis A parallel to an axis through the center of mass. If axis A is 0.20 m from the center of mass axis, the rotational inertia about the center of mass axis isA) 0.40 kg · m2.
B) 2.0 kg · m2.
C) 2.4 kg · m2.
D) 2.8 kg · m2.
E) 4.4 kg · m2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
22
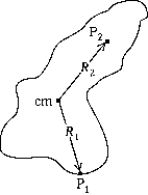 In the figure, R1 = R2 and cm represents the center of mass of the object. The rotational inertia about an axis through point P1 is I1, the rotational inertia about an axis through point P2 is I2, and the rotational inertia about an axis through the cm is Icm. The relationship among the moments is
In the figure, R1 = R2 and cm represents the center of mass of the object. The rotational inertia about an axis through point P1 is I1, the rotational inertia about an axis through point P2 is I2, and the rotational inertia about an axis through the cm is Icm. The relationship among the moments isA) I1 = I2 > Icm.
B) I1 = I2 < Icm.
C) I1 > I2 > Icm.
D) I1 < Icm > I2.
E) I1 = I2 = Icm.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
23
The rotational inertia of an object about an axis depends on the
A) angular velocity about the axis.
B) angular acceleration about the axis.
C) mass distribution about the axis.
D) torque about the axis.
E) linear acceleration about the axis.
A) angular velocity about the axis.
B) angular acceleration about the axis.
C) mass distribution about the axis.
D) torque about the axis.
E) linear acceleration about the axis.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
24
A uniform cylinder I = mR2) of diameter 0.20 m and mass 12 kg rolls without slipping down a 37o inclined plane. The gain in translational kinetic energy of the cylinder when it has rolled 5 m down the incline of the plane is approximately
A) 24 J.
B) 0.12 kJ.
C) 0.24 kJ.
D) 0.35 kJ.
E) 0.59 kJ.
A) 24 J.
B) 0.12 kJ.
C) 0.24 kJ.
D) 0.35 kJ.
E) 0.59 kJ.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
25
A wheel rotates through 6.0 rad in 2.0 s as it is uniformly brought to rest. The initial angular velocity of the wheel before braking began was
A) 0.60 rad/s.
B) 0.90 rad/s.
C) 1.8 rad/s.
D) 6.0 rad/s.
E) 7.2 rad/s.
A) 0.60 rad/s.
B) 0.90 rad/s.
C) 1.8 rad/s.
D) 6.0 rad/s.
E) 7.2 rad/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
26
For a hoop ring) of mass M and radius R that is rolling without slipping, which is greater, its translational or its rotational kinetic energy?
A) Its translational kinetic energy is greater.
B) Its rotational kinetic energy is greater.
C) They are equal.
D) The answer depends on the radius.
E) The answer depends on the mass.
A) Its translational kinetic energy is greater.
B) Its rotational kinetic energy is greater.
C) They are equal.
D) The answer depends on the radius.
E) The answer depends on the mass.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
27
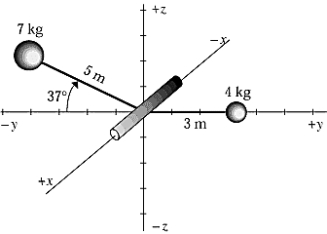 A 7.00-kg mass and a 4.00-kg mass are mounted on a spindle, free to turn about the x axis as shown. Assume the mass of the arms and the spindle to be negligible. The rotational inertia of this system is approximately
A 7.00-kg mass and a 4.00-kg mass are mounted on a spindle, free to turn about the x axis as shown. Assume the mass of the arms and the spindle to be negligible. The rotational inertia of this system is approximatelyA) 44.0 kg · m2.
B) 47.0 kg · m2.
C) 99.0 kg · m2.
D) 148 kg · m2.
E) 211 kg · m2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
28
A solid uniform sphere has a density of 3000 kg/m3 when the radius is equal to 0.6 m. If the mass stayed the same but the radius tripled in size, what would the new moment of inertia be for the sphere?
A) 98.0 kg m2
B) 879 kg m2
C) 294 kg m2
D) 196 kg m2
E) 2650 kg m2
A) 98.0 kg m2
B) 879 kg m2
C) 294 kg m2
D) 196 kg m2
E) 2650 kg m2

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
29
Two objects, m1 and m2, both of mass m, are placed on a horizontal platform which is rotating at a constant angular velocity. m1 is located at a distance R from the axis of rotation and m2 is located at a R. The tangential acceleration of mass m1 ____ the tangential acceleration of m2.
A) is less than
B) is equal to
C) is greater than
D) is independent of
E) Unable to tell.
A) is less than
B) is equal to
C) is greater than
D) is independent of
E) Unable to tell.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
30
The moment of inertia of a certain wheel about its axle is mR2. The translational speed of its axle after it starts from rest and rolls without slipping down an inclined plane 2.13 m high is
A) 9.75 m/s.
B) 8.53 m/s.
C) 7.31 m/s.
D) 6.10 m/s.
E) 4.88 m/s.
A) 9.75 m/s.
B) 8.53 m/s.
C) 7.31 m/s.
D) 6.10 m/s.
E) 4.88 m/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
31
A bicycle wheel, a hollow sphere, and a solid sphere each have the same mass and radius. They each rotate about an axis through their centers. Which has the greatest moment of inertia and which has the least?
A) The wheel has the greatest; the solid sphere has the least.
B) The wheel has the greatest; the hollow sphere has the least.
C) The hollow sphere has the greatest; the solid sphere has the least.
D) The hollow sphere has the greatest; the wheel has the least.
E) The solid sphere has the greatest; the hollow sphere has the least.
A) The wheel has the greatest; the solid sphere has the least.
B) The wheel has the greatest; the hollow sphere has the least.
C) The hollow sphere has the greatest; the solid sphere has the least.
D) The hollow sphere has the greatest; the wheel has the least.
E) The solid sphere has the greatest; the hollow sphere has the least.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
32
Assume that all of the mass of a bicycle wheel is concentrated at its rim. Such a wheel of mass 1.2 kg and radius 30 cm starts from rest at the top of a hill 100 m long and inclined at 20o to the horizontal. What will the speed of the wheel be at the bottom of the hill if it rolls without slipping?
A) 21 m/s
B) 26 m/s
C) 15 m/s
D) 33 m/s
E) 37 m/s
A) 21 m/s
B) 26 m/s
C) 15 m/s
D) 33 m/s
E) 37 m/s

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
33
A record turntable rotates through 5.0 rad in 2.8 s as it is accelerated uniformly from rest. What is the angular velocity at the end of that time?
A) 0.60 rad/s
B) 0.90 rad/s
C) 1.8 rad/s
D) 3.6 rad/s
E) 14 rad/s
A) 0.60 rad/s
B) 0.90 rad/s
C) 1.8 rad/s
D) 3.6 rad/s
E) 14 rad/s

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
34
A 5-kg block is attached to a pulley by a light rope. The rope is wound around the pulley, and when the block is released, the rope unspools without slipping. The pulley is a solid disk of radius 0.2 m and mass 2 kg. What is the approximate angular speed of the pulley when the block has fallen 1 meter?
A) 0.7 rad/s
B) 7.0 rad/s
C) 15.7 rad/s
D) 22.2 rad/s
E) The answer cannot be determined without knowing the final speed of the block.
A) 0.7 rad/s
B) 7.0 rad/s
C) 15.7 rad/s
D) 22.2 rad/s
E) The answer cannot be determined without knowing the final speed of the block.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
35
For a disk of mass M and radius R that is rolling without slipping, which is greater, its translational or its rotational kinetic energy?
A) Its translational kinetic energy is greater.
B) Its rotational kinetic energy is greater.
C) They are equal.
D) The answer depends on the radius.
E) The answer depends on the mass.
A) Its translational kinetic energy is greater.
B) Its rotational kinetic energy is greater.
C) They are equal.
D) The answer depends on the radius.
E) The answer depends on the mass.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
36
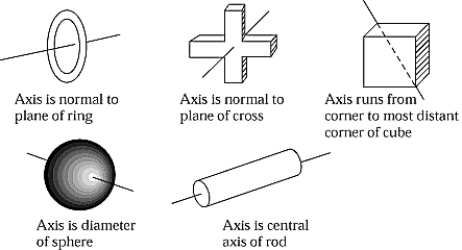 If all of the objects illustrated in the figure have equal masses, the moment of inertia about the indicated axis is largest for the
If all of the objects illustrated in the figure have equal masses, the moment of inertia about the indicated axis is largest for theA) ring.
B) cross.
C) sphere.
D) cube.
E) rod.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
37
A uniform disk Io = ½ mR2) of mass m and radius R is suspended from a point on its rim. The moment of inertia of the disk about an axis perpendicular to the disk through the pivot point is
A) ½ mR2.
B) mR2.
C) 1.5mR2.
D) 2mR2.
E) 2mR2/3.
A) ½ mR2.
B) mR2.
C) 1.5mR2.
D) 2mR2.
E) 2mR2/3.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
38
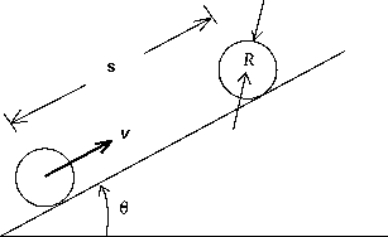
A solid disk Icm =
 mR2) rolls without slipping up a plane a distance s. The plane is inclined at an angle θ with the horizontal. The disk has mass m, radius R, and an initial translational speed v. The distance s the disk rolls is
mR2) rolls without slipping up a plane a distance s. The plane is inclined at an angle θ with the horizontal. The disk has mass m, radius R, and an initial translational speed v. The distance s the disk rolls isA)
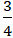 v2/g sin θ ).
v2/g sin θ ).B) 11ec81b1_0372_75b9_8138_b76fd7fac723_TB7291_11v2/g sin θ ).
C) 11ec81b1_0372_75b9_8138_b76fd7fac723_TB7291_11Rv/g sin θ ).
D) 11ec81b1_0372_75b9_8138_b76fd7fac723_TB7291_11mgsin θ - cos θ )Rv)2.
E) v2/g sin θ ).

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
39
A uniform cylinder I = mR2) of diameter 0.20 m and mass 12 kg rolls without slipping down a 37o inclined plane. The acceleration of the cylinder down the plane is approximately
A) 2.0 m/s2.
B) 3.9 m/s2.
C) 4.9 m/s2.
D) 5.8 m/s2.
E) 9.8 m/s2.
A) 2.0 m/s2.
B) 3.9 m/s2.
C) 4.9 m/s2.
D) 5.8 m/s2.
E) 9.8 m/s2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
40
Starting from rest, a disk rotates with constant angular acceleration. If it takes 10 rev to reach an angular velocity , then how many additional revolutions are required to reach an angular velocity 2?
A) 10 rev
B) 20 rev
C) 30 rev
D) 40 rev
E) 50 rev
A) 10 rev
B) 20 rev
C) 30 rev
D) 40 rev
E) 50 rev

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
41
You are whirling a stone on the end of a string in a horizontal circle of radius R = 0.65 m with a frequency of 4 rev/s when the string breaks. Just after the string breaks, the velocity of the stone is
A) straight down.
B) 32 m/s along a tangent to the circle.
C) 16 m/s along the radius away from the center.
D) 1.0 m/s along the radius toward the center.
E) none of these.
A) straight down.
B) 32 m/s along a tangent to the circle.
C) 16 m/s along the radius away from the center.
D) 1.0 m/s along the radius toward the center.
E) none of these.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
42
A wheel rotates with a constant nonzero angular acceleration. Which of the following quantities remains constant in magnitude?
A) v ⃗, tangential velocity
B) a ⃗r, radial acceleration
C) at ⃗ , tangential acceleration
D) ω ⃗, angular velocity
E) All of these are correct.
A) v ⃗, tangential velocity
B) a ⃗r, radial acceleration
C) at ⃗ , tangential acceleration
D) ω ⃗, angular velocity
E) All of these are correct.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
43
A wheel slows from 20 rad/s to 12 rad/s in 5 s under the influence of a constant frictional torque. In these 5 s, the wheel turns through an angle of
A) 2.4 rad.
B) 43 rad.
C) 60 rad.
D) 80 rad.
E) 100 rad.
A) 2.4 rad.
B) 43 rad.
C) 60 rad.
D) 80 rad.
E) 100 rad.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
44
The Crab Pulsar rotates 30 times per second. However, its period is increasing by about s per year. How many years will it take before its period of rotation has doubled?
A) 3.0 106 yr
B) 6.7 103 yr
C) 3.3 103 yr
D) 1.05 1010 yr
E) 2.10 1010 yr
A) 3.0 106 yr
B) 6.7 103 yr
C) 3.3 103 yr
D) 1.05 1010 yr
E) 2.10 1010 yr

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
45
Torque is defined as
A) a force tending to cause rotation.
B) the cross product of force and displacement.
C) the product of the force and the angular displacement.
D) the product of the force and the angular velocity.
E) the rotational work done.
A) a force tending to cause rotation.
B) the cross product of force and displacement.
C) the product of the force and the angular displacement.
D) the product of the force and the angular velocity.
E) the rotational work done.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
46
The torque exerted on a perfectly spherical satellite by the gravitational pull of the sun is
A) zero.
B) directed along Earth's axis to the north pole.
C) directed along Earth's axis to the south pole.
D) in the direction of Earth's orbit.
E) directed toward the sun.
A) zero.
B) directed along Earth's axis to the north pole.
C) directed along Earth's axis to the south pole.
D) in the direction of Earth's orbit.
E) directed toward the sun.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
47
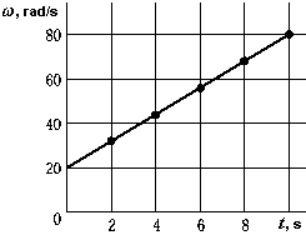 The data used to construct the graph were taken from the tachometer of an airplane a tachometer measures the angular speed of an engine). The angular acceleration during the 10 s interval was
The data used to construct the graph were taken from the tachometer of an airplane a tachometer measures the angular speed of an engine). The angular acceleration during the 10 s interval wasA) "3.0 rad/s2. "
B) "6.0 rad/s2. "
C) "8.0 rad/s2. "
D) "20 rad/s2. "
E) "38 rad/s2. "

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
48
A turntable rotating at 8.0 rad/s slows to a stop in 10 s. If the acceleration is constant, the angle through which the turntable rotates in the 10 s is
A) 0.80 rad.
B) 0.40 rad.
C) 40 rad.
D) 80 rad.
E) 16 rad.
A) 0.80 rad.
B) 0.40 rad.
C) 40 rad.
D) 80 rad.
E) 16 rad.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
49
Two blocks m1 = 0.4 kg) and m2 = 0.6 kg) are initially positioned at x = 0.6 and x = 1.1m. One cord is used to couple the blocks together and another to attach m1 to a vertical pole at the origin. The blocks are made to rotate in a horizontal circle on a frictionless surface. If the period of rotation is 0.4 s, then calculate the ratio of the tension for the inner cord divided by the tension in the outer cord.
A) 0.64
B) 1.4
C) 1.6
D) 0.74
E) 1.8
A) 0.64
B) 1.4
C) 1.6
D) 0.74
E) 1.8

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
50
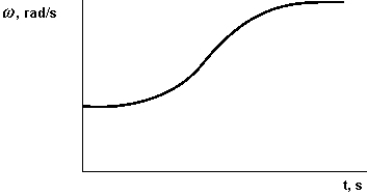 What physical quantity is represented by the slope of the curve shown on the graph?
What physical quantity is represented by the slope of the curve shown on the graph?A) displacement
B) angular acceleration
C) tangential acceleration
D) velocity
E) None of these is correct.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
51
A wheel starting from rest has a constant angular acceleration. After 3.0 s the angular velocity of the wheel is 7.5 rad/s. This same angular acceleration continues for a further 7.0 s after which it drops suddenly to zero. In the first 20.0 s how many revolutions does the wheel make?
A) 20
B) 40
C) 60
D) 80
E) 100
A) 20
B) 40
C) 60
D) 80
E) 100

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
52
Water is drawn from a well in a bucket tied to the end of a rope whose other end wraps around a cylinder of mass 50 kg and diameter 25 cm. As you turn this cylinder with a crank, the rope raises the bucket. If the mass of a bucket of water is 20 kg, what torque must you apply to the crank to raise the bucket of water at a constant speed?
A) 24 N · m
B) 2.5 N · m
C) 80 N · m
D) 2.4 103 N · m
E) 49 N · m
A) 24 N · m
B) 2.5 N · m
C) 80 N · m
D) 2.4 103 N · m
E) 49 N · m

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
53
When an object is moving in a circle at constant speed, its acceleration is
A) constantly increasing.
B) constant in direction.
C) zero.
D) constant in magnitude.
E) constant in both magnitude and direction.
A) constantly increasing.
B) constant in direction.
C) zero.
D) constant in magnitude.
E) constant in both magnitude and direction.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
54
A uniform stick 1 m long is placed horizontally on the ground along an east-west axis. A force of 1.0 N is applied to the center of the stick in a direction 30o west of north. The torque exerted by the force relative to the east end of the stick is
A) zero.
B) 0.25 m, clockwise.
C) 0.43 m, clockwise.
D) 0.25 m, counterclockwise.
E) 0.43 m, counterclockwise.
A) zero.
B) 0.25 m, clockwise.
C) 0.43 m, clockwise.
D) 0.25 m, counterclockwise.
E) 0.43 m, counterclockwise.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
55
The Empire's space station is a long way from any star. It is circular and has a radius of 5.10 km. The angular velocity that is needed to give the station an artificial gravity of 9.80 m/s2 at its circumference is
A) 4.4 10-2 rad/s.
B) 7.0 10-3 rad/s.
C) 0.28 rad/s.
D) - 0.22 rad/s.
E) 1.3 103 rad/s.
A) 4.4 10-2 rad/s.
B) 7.0 10-3 rad/s.
C) 0.28 rad/s.
D) - 0.22 rad/s.
E) 1.3 103 rad/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
56
A point P is at a distance R from the axis of rotation of a rigid body. The linear speed, centripetal acceleration, and tangential acceleration of the point can be expressed 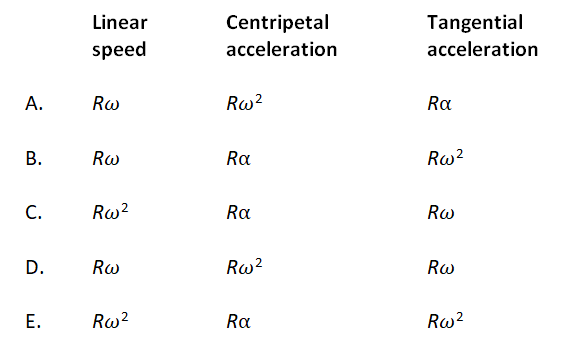
A)A
B)B
C)C
D)D
E)E

A)A
B)B
C)C
D)D
E)E

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
57
You are pedaling a bicycle at 9.8 m/s. The radius of the wheels of the bicycle is 51.9 cm. The angular velocity of rotation of the wheels is
A) 19 rad/s.
B) 2.5 rad/s.
C) 4.5 rad/s.
D) 3.0 rad/s.
E) 6.3 rad/s.
A) 19 rad/s.
B) 2.5 rad/s.
C) 4.5 rad/s.
D) 3.0 rad/s.
E) 6.3 rad/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
58
The information on a compact disk is scanned by a laser initially at a radius of 2.4 cm and then out to a maximum of 6.0 cm. Because the dimensions of the pit information remain constant with radius, the disk motor adjusts so that the tangential velocity remains constant. What is the ratio of the inner to outer rotational frequencies?
A) 0.16
B) 6.3
C) 1.0
D) 2.5
E) 0.40
A) 0.16
B) 6.3
C) 1.0
D) 2.5
E) 0.40

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
59
A serious audiophile prefers to listen to music on his vinyl record turntable. The 12-inch diameter disk rotates at a constant 33 rpm. How fast is the record passing by the pickup cartridge tip at a radius of 4 inches 1 inch = 2.54 cm)?
A) 5.6 cm/s
B) 35 cm/s
C) 3.3 102 cm/s
D) 21 m/s
E) 18 cm/s
A) 5.6 cm/s
B) 35 cm/s
C) 3.3 102 cm/s
D) 21 m/s
E) 18 cm/s

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
60
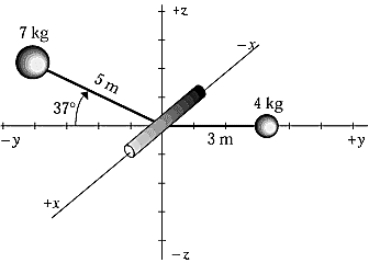 A 7.00-kg mass and a 4.00-kg mass are mounted on a spindle that is free to turn about the x axis as shown. Assume the mass of the arms and the spindle to be negligible. The magnitude of the resultant torque is approximately
A 7.00-kg mass and a 4.00-kg mass are mounted on a spindle that is free to turn about the x axis as shown. Assume the mass of the arms and the spindle to be negligible. The magnitude of the resultant torque is approximatelyA) 82.2 N · m.
B) 157 N · m.
C) 225 N · m.
D) 392 N · m.
E) 461 N · m.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
61
A spherical shell and a solid sphere both of the same total mass) are rotating about a diameter at the same angular frequency and with the same rotational kinetic energy. What is the ratio of the spherical shell radius to the solid sphere i.e., Rspherical shell/Rsolid sphere)?
A) 2/5)1/2
B) 3/10)1/2
C) 1/2)1/2
D) 3/5)1/2
E) 2/3)1/2
A) 2/5)1/2
B) 3/10)1/2
C) 1/2)1/2
D) 3/5)1/2
E) 2/3)1/2

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
62
A disk with a radius of 1.5 m whose moment of inertia is 34 kg m2 is caused to rotate by a force of 160 N tangent to the circumference. The angular acceleration of the disk is approximately
A) 0.14 rad/s2.
B) 0.23 rad/s2.
C) 4.4 rad/s2.
D) 7.1 rad/s2.
E) 23 rad/s2.
A) 0.14 rad/s2.
B) 0.23 rad/s2.
C) 4.4 rad/s2.
D) 7.1 rad/s2.
E) 23 rad/s2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
63
A body that moves with a constant speed in a circle
A) experiences no acceleration.
B) undergoes no change in velocity.
C) has no resultant force acting on it.
D) has no work done on it.
E) is described by all of these.
A) experiences no acceleration.
B) undergoes no change in velocity.
C) has no resultant force acting on it.
D) has no work done on it.
E) is described by all of these.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
64
The torque exerted on a perfectly spherical orbiting communications satellite by the gravitational pull of Earth is
A) directed toward Earth.
B) directed parallel to Earth's axis and toward the north pole.
C) directed parallel to Earth's axis and toward the south pole.
D) directed toward the satellite.
E) zero.
A) directed toward Earth.
B) directed parallel to Earth's axis and toward the north pole.
C) directed parallel to Earth's axis and toward the south pole.
D) directed toward the satellite.
E) zero.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
65
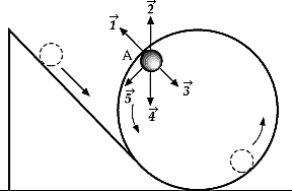 The ball shown in the figure will loop-the-loop if it starts from a point high enough on the incline. When the ball is at point A, the centripetal force on it is best represented by which of the following vectors?
The ball shown in the figure will loop-the-loop if it starts from a point high enough on the incline. When the ball is at point A, the centripetal force on it is best represented by which of the following vectors?A)
B)
C)
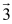
D)
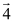
E)
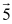

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
66
A 0.3-kg object is being whirled in a horizontal circle at the end of a 1.5 m long string. If the string breaks when the number of revolutions per minute, rpm = 200, then find the maximum tension in the string.
A) 2.0 102 N
B) 59 N
C) 7.0 105 N
D) 9.0 N
E) 88 N
A) 2.0 102 N
B) 59 N
C) 7.0 105 N
D) 9.0 N
E) 88 N

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
67
A disk-shaped grindstone of mass 3.0 kg and radius 8.0 cm is spinning at 600 rev/min. After the power is shut off, a man continues to sharpen his axe by holding it against the grindstone until it stops 10 s later. What is the average torque exerted by the axe on the grindstone?
A) 9.6 mN · m
B) 0.12 N · m
C) 0.75 N · m
D) 0.60 kN · m
E) 0.060 N · m
A) 9.6 mN · m
B) 0.12 N · m
C) 0.75 N · m
D) 0.60 kN · m
E) 0.060 N · m

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
68
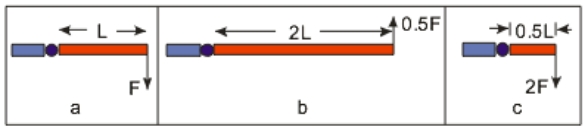 The diagrams above show the application of a force to a level arm. Which diagram has the largest magnitude) torque about the hinge?
The diagrams above show the application of a force to a level arm. Which diagram has the largest magnitude) torque about the hinge?A) a
B) b
C) c
D) They are the same.
E) Unable to determine.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
69
A cylinder I = ½mR2) rolls along a level floor with a speed v. The work required to stop this cylinder is
A) ¼ mv2.
B) ½ mv2.
C) ¾ mv2.
D) mv2.
E) 1.25mv2.
A) ¼ mv2.
B) ½ mv2.
C) ¾ mv2.
D) mv2.
E) 1.25mv2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
70
What constant torque, in the absence of friction, must be applied to a wheel to give it an angular velocity of 50 rad/s if it starts from rest and is accelerated for 10 s? The moment of inertia of the wheel about its axle is 9.0 kg · m2.
A) 4.5 N · m
B) 9.0 N · m
C) 45 N · m
D) 30 N · m
E) 60 N · m
A) 4.5 N · m
B) 9.0 N · m
C) 45 N · m
D) 30 N · m
E) 60 N · m

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
71
A thin solid disk of radius R = 0.5 m and mass M = 2.0 kg is rolling without slipping on a horizontal surface with a linear speed v = 5.0 m/s. The disk now rolls without slipping up an inclined plane that is at an angle of 60 degrees to the vertical. Calculate the maximum height that the disk rolls up the incline.
A) 5.1 m
B) 2.6 m
C) 2.9 m
D) 3.1 m
E) 1.3 m
A) 5.1 m
B) 2.6 m
C) 2.9 m
D) 3.1 m
E) 1.3 m

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
72
A 5 10-6-kg dot of paint on the side of a rotating cylinder flies off when the angular speed of the cylinder reaches 5 103 rad/s. The spin axis of the cylinder is vertical and its radius is 0.04 m. The force of adhesion between the paint and the surface is approximately
A) 1 N.
B) 1 mN.
C) 5 mN.
D) 5 kN.
E) 5 N.
A) 1 N.
B) 1 mN.
C) 5 mN.
D) 5 kN.
E) 5 N.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
73
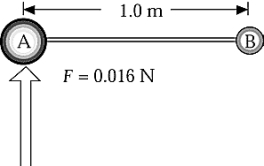 Two small masses, mA = 4.0 10-3 kg and mB = 2.0 10-3 kg, are connected by a 1.0-m rod of negligible mass. The angular acceleration about B produced by a force of 0.016 N applied at A is approximately
Two small masses, mA = 4.0 10-3 kg and mB = 2.0 10-3 kg, are connected by a 1.0-m rod of negligible mass. The angular acceleration about B produced by a force of 0.016 N applied at A is approximatelyA) 4.0 rad/s2.
B) 2.7 rad/s2.
C) 11 rad/s2.
D) 12 rad/s2.
E) 4.0 102 rad/s2.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
74
A turntable has an angular velocity of 1.4 rad/s. The coefficient of static friction between the turntable and a block placed on it is 0.20. The maximum distance from the center of the turntable that the block can be placed without sliding is approximately
A) 0.50 m.
B) 1.0 m.
C) 1.4 m.
D) 2.0 m.
E) 4.4 m.
A) 0.50 m.
B) 1.0 m.
C) 1.4 m.
D) 2.0 m.
E) 4.4 m.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
75
A solid sphere I = 0.4MR2) of radius 0.06 m and mass 0.50 kg rolls without slipping 14 m down a 30° inclined plane. At the bottom of the plane, the linear velocity of the center of mass of the sphere is approximately
A) 3.5 m/s.
B) 3.9 m/s.
C) 8.7 m/s.
D) 18 m/s.
E) 9.9 m/s.
A) 3.5 m/s.
B) 3.9 m/s.
C) 8.7 m/s.
D) 18 m/s.
E) 9.9 m/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
76
A penny is placed 0.10 m from the center of a turntable. If the coefficient of static friction between the penny and the turntable is 0.50, the maximum linear speed at which the penny can travel without slipping is approximately
A) 0.49 m/s.
B) 0.70 m/s.
C) 1.3 m/s.
D) 1.4 m/s.
E) 0.20 km/s.
A) 0.49 m/s.
B) 0.70 m/s.
C) 1.3 m/s.
D) 1.4 m/s.
E) 0.20 km/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
77
Two masses M and m M > m) are hung over a disk Idisk = M'R2) and are released so that they accelerate. If T1 is the tension in the cord on the left and T2 is the tension in the cord on the right, then
A) T1 = T2.
B) T2 > T1.
C) T2 < T1.
D) T2 = Mg.
E) T2 = Mg/m.
A) T1 = T2.
B) T2 > T1.
C) T2 < T1.
D) T2 = Mg.
E) T2 = Mg/m.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
78
 The diagrams above show the application of a force to a level arm. The arms are of the same length and = 30o. Which diagram has the largest magnitude) torque about the hinge?
The diagrams above show the application of a force to a level arm. The arms are of the same length and = 30o. Which diagram has the largest magnitude) torque about the hinge?A) a
B) b
C) c
D) d
E) They are the same.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
79
Water is drawn from a well in a bucket tied to the end of a rope whose other end wraps around a solid cylinder of mass 50 kg and diameter 25 cm. As this cylinder is turned with a crank, the rope raises the bucket. The mass of a bucket of water is 20 kg. Someone cranks the bucket up, lets go of the crank, and the bucket of water falls down to the bottom of the well. Without friction or air resistance, what is the angular acceleration of the 50-kg cylinder?
A) 1.1 102 rad/s2
B) 3.6 rad/s2
C) 35 rad/s2
D) 63 rad/s2
E) 17 rad/s2
A) 1.1 102 rad/s2
B) 3.6 rad/s2
C) 35 rad/s2
D) 63 rad/s2
E) 17 rad/s2

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck
80
The moment of inertia of a certain cylinder, whose mass is not distributed uniformly, is 0.6mR2 about its geometric axis. The translational speed of the center of mass after it starts from rest and rolls 14 m down a 30° incline is approximately
A) 9.3 m/s.
B) 86 m/s.
C) 13 m/s.
D) 3.1 m/s.
E) 41 m/s.
A) 9.3 m/s.
B) 86 m/s.
C) 13 m/s.
D) 3.1 m/s.
E) 41 m/s.

Unlock Deck
Unlock for access to all 130 flashcards in this deck.
Unlock Deck
k this deck


