Deck 10: Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/68
Play
Full screen (f)
Deck 10: Sampling Distributions
1
A sample of size 50 is to be taken from an infinite population whose mean and standard deviation are 52 and 20, respectively. The probability that the sample mean will be larger than 49 is: 

C
2
If all possible samples of size n are drawn from an infinite population with mean and standard deviation , then the standard error of the sample mean is inversely proportional to:
D
3
Given an infinite population with a mean of 75 and a standard deviation of 12, the probability that the mean of a sample of 36 observations, taken at random from this population, exceeds 78 is: 

B
4
The finite population correction factor should not be used when: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
5
If all possible samples of size n are drawn from a population, the probability distribution of the sample mean 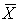 is called the:
is called the: 
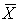 is called the:
is called the: 

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
6
As a general rule in computing the standard error of the sample mean, the finite population correction factor is used only if the: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
7
A normally distributed population with 200 elements has a mean of 60 and a standard deviation of 10. The probability that the mean of a sample of 25 elements taken from this population will be smaller than 56 is: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
8
Random samples of size 64 are taken from an infinite population whose mean is 160 and standard deviation is 32. The mean and standard error of the sample mean, respectively, are: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
9
If a random sample of size n is drawn from a normal population, then the sampling distribution of the sample mean 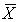 will be:
will be: 
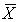 will be:
will be: 

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
10
The standard deviation of the sampling distribution of the sample mean is also called the: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
11
Consider an infinite population with a mean of 160 and a standard deviation of 25. A random sample of size 64 is taken from this population. The standard deviation of the sample mean equals: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
12
If all possible samples of size n are drawn from an infinite population with a mean of 15 and a standard deviation of 5, then the standard error of the sample mean equals 1.0 only for samples of size: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
13
A population that consists of 250 items has a mean of 37 and a standard deviation of 13. A sample of size 5 is taken at random from this population. The standard error of the sample mean equals (up to three decimal places): 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
14
An infinite population has a mean of 33 and a standard deviation of 6. A sample of 100 observations is to be taken at random from this population. The probability that the sample mean will be between 34.5 and 36.1 is: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
15
A sample of size n is selected at random from an infinite population. As n increases, which of the following statements is true?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
16
A sample of size 35 is selected at random from a finite population. If the finite population correction factor is 0.5, then (rounded to the nearest integer) the population size is: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
17
Random samples of size 81 are taken from an infinite population whose mean and standard deviation are 45 and 9, respectively. The mean and standard error of the sampling distribution of the sample mean are: 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
18
The central limit theorem states that if a random sample of size n is drawn from a population, then the sampling distribution of the sample mean 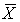 :
: 
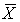 :
: 

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following best describes the Central Limit Theorem? 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
20
The expected value of the sampling distribution of the sample mean equals the population mean :

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
21
A sample of size n is selected at random from an infinite population. As n increases the standard error of the sample mean decreases.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
22
When a great many simple random samples of size n are drawn from a population that is normally distributed, the sampling distribution of the sample means will be normal, regardless of sample size n.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
23
If all possible samples of size n are drawn from a population, the probability distribution of the sample mean is referred to as the normal distribution.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
24
The sampling distribution of the sample proportion has mean p and variance pq/n.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
25
If the daily demand for boxes of mineral water at a supermarket is normally distributed with a mean of 47.6 boxes and a standard deviation of 5.8 boxes, what is the probability that the average demand for a sample of 10 supermarkets will be less than 50 boxes in a given day?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
26
The sampling distribution of the sample proportion is approximately normal provided that np ≥ 5 and nq ≥ 5

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
27
It is know that 40% of voters in a certain electorate are in favour of a particular candidate. If a sample of size 30 is taken, what is the probability that less than 35% are in favour of this political candidate? 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following best describes the sampling distribution of the sample proportion? 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
29
The standard deviation of a sampled population is also called the standard error of the sample mean.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose that the time needed to complete a final exam is normally distributed with a mean of 85 minutes and a standard deviation of 18 minutes.
a. What is the probability that the total time taken by a group of 100 students will not exceed 8200 minutes?
b. What assumption did you have to make in your computations in part (a)?
a. What is the probability that the total time taken by a group of 100 students will not exceed 8200 minutes?
b. What assumption did you have to make in your computations in part (a)?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
31
A manufacturing company is concerned about the number of defective items produced by their assembly line. In the past they have had 5% of their products produced defectively. They take a random sample of 35 products. What is the probability that more than 5 products in the sample are defective? 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
32
A researcher conducted a survey on a university campus for a sample of 64 third-year students and reported that third-year students read an average of 3.12 books in the prior academic semester, with a standard deviation of 2.15 books. Determine the probability that the sample mean is:
a. less than 3.45.
b. between 3.38 and 3.58.
c. above 2.94.
a. less than 3.45.
b. between 3.38 and 3.58.
c. above 2.94.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
33
Consider an infinite population with a mean of 100 and a standard deviation of 20. A random sample of size 50 is taken from this population. The standard deviation of the sample mean equals 3.2.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
34
The sampling distribution of the sample proportion is always normally distributed.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
35
If it is known that the population proportion of car parks in a particular city that offer early discount fees is 25%, which of the following best describes the mean and standard deviation of the sampling distribution of the sample proportion of car parks that offer early discount fees for samples taken of size 30? 


Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
36
The standard error of the mean is the standard deviation of the sampling distribution of .

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
37
If all possible samples of size n are drawn from an infinite population with a mean of 60 and a standard deviation of 8, then the standard error of the sample mean equals 1.0 only for samples of size 64.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
38
A sample of size 70 is selected at random from a finite population. If the finite population correction factor is 0.808, the population size (rounded to the nearest integer) must be 200.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
39
The central limit theorem is basic to the concept of statistical inference, because it permits us to draw conclusions about the population based strictly on sample data, and without having any knowledge about the distribution of the underlying population.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
40
An infinite population has a mean of 120 and a standard deviation of 44. A sample of 100 observations is to be selected at random from the population.
a. What is the expected value of the sample mean?
b. What is the standard deviation of the sample mean?
c. What is the shape of the sampling distribution of the sample mean?
d. What does the sampling distribution of the sample mean show?
a. What is the expected value of the sample mean?
b. What is the standard deviation of the sample mean?
c. What is the shape of the sampling distribution of the sample mean?
d. What does the sampling distribution of the sample mean show?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
41
A sample of 30 observations is drawn from a normal population with mean of 750 and a standard deviation of 300. Suppose the population size is 600.
a. Find the expected value of the sample mean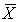 .
.
b. Find the standard error of the sample mean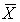 .
.
c. Find P(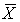 > 790).
> 790).
d. Find P(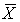 < 650).
< 650).
e. Find P(760 <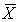 < 810).
< 810).
a. Find the expected value of the sample mean
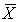 .
.b. Find the standard error of the sample mean
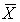 .
.c. Find P(
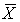 > 790).
> 790).d. Find P(
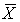 < 650).
< 650).e. Find P(760 <
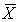 < 810).
< 810).
Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
42
The amount of time spent by Australian adults playing sports per day is normally distributed, with a mean of 4 hours and standard deviation of 1.25 hours. Use this information to answer the following question(s).
Find the probability that a randomly selected Australian adult plays sport for more than 5 hours per day.
Find the probability that a randomly selected Australian adult plays sport for more than 5 hours per day.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
43
The heights of 9-year-old children are normally distributed, with a mean of 123 cm and a standard deviation of 10 cm.
a. Find the probability that one randomly selected 9-year-old child is taller than 125 cm.
b. Find the probability that three randomly selected 9-year-old children are taller than 125 cm.
c. Find the probability that the mean height of three randomly selected 9-year-old children is greater than 125 cm.
a. Find the probability that one randomly selected 9-year-old child is taller than 125 cm.
b. Find the probability that three randomly selected 9-year-old children are taller than 125 cm.
c. Find the probability that the mean height of three randomly selected 9-year-old children is greater than 125 cm.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
44
The heights of women in Australia are normally distributed, with a mean of 165 centimetres and a standard deviation of 10 centimetres. What is the probability that the mean height of a random sample of 30 women is smaller than 162 centimetres?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
45
The amount of time spent by Australian adults playing sports per day is normally distributed, with a mean of 4 hours and standard deviation of 1.25 hours. Find the probability that if four Australian adults are randomly selected, their average number of hours spent playing sport is more than 5 hours per day.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
46
A sample of size 400 is drawn from a population whose mean and variance are 5000 and 10 000, respectively. Find the following probabilities.
a. P(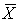 < 4,990).
< 4,990).
b. P(4995 <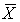 < 5010).
< 5010).
c. P(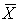 = 5000).
= 5000).
a. P(
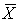 < 4,990).
< 4,990).b. P(4995 <
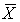 < 5010).
< 5010).c. P(
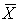 = 5000).
= 5000).
Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
47
The amount of time spent by Australian adults playing sports per day is normally distributed, with a mean of 4 hours and standard deviation of 1.25 hours. Find the probability that if four Australian adults are randomly selected, all four play sport for more than 5 hours per day.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
48
An auditor knows from past history that the average accounts receivable for a company is $521.72, with a standard deviation of $584.64. If the auditor takes a simple random sample of 100 accounts, what is the probability that the mean of the sample will be within $120 of the population mean?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
49
The heights of women in Australia are normally distributed, with a mean of 165 centimetres and a standard deviation of 10 centimetres. If the population of women's heights were not normally distributed, which, if any, of the following questions could you answer?
A) What is the probability that a randomly selected woman is taller than 160 cm?
B) A random sample of five women is selected. What is the probability that the sample mean is greater than 160 cm?
C) What is the probability that the mean height of a random sample of 75 women is greater than 160 cm?
A) What is the probability that a randomly selected woman is taller than 160 cm?
B) A random sample of five women is selected. What is the probability that the sample mean is greater than 160 cm?
C) What is the probability that the mean height of a random sample of 75 women is greater than 160 cm?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
50
The heights of women in Australia are normally distributed, with a mean of 165 centimetres and a standard deviation of 10 centimetres. Use this information to answer the following question(s).
What is the probability that a randomly selected woman is shorter than 162 centimetres?
What is the probability that a randomly selected woman is shorter than 162 centimetres?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose that the average annual income of a lawyer is $150 000 with a standard deviation of $40 000. Assume that the income distribution is normal.
a. What is the probability that the average annual income of a sample of 5 lawyers is more than $120 000?
b. What is the probability that the average annual income of a sample of 15 lawyers is more than $120 000?
a. What is the probability that the average annual income of a sample of 5 lawyers is more than $120 000?
b. What is the probability that the average annual income of a sample of 15 lawyers is more than $120 000?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
52
The heights of women in Australia are normally distributed, with a mean of 165 centimetres and a variance of 100 centimetres2. A random sample of five women is selected. What is the probability that the sample mean is greater than 162 centimetres?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
53
Assume that the time needed by a worker to perform a maintenance operation is normally distributed, with a mean of 60 minutes and a standard deviation of 6 minutes. What is the probability that the average time needed by a sample of 5 workers to perform the maintenance is between 63 and 68 minutes?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
54
A sample of 50 observations is drawn at random from a normal population whose mean and standard deviation are 75 and 6, respectively.
a. What does the central limit theorem say about the sampling distribution of the sample mean? Why?
b. Find the mean and standard error of the sampling distribution of the sample mean.
c. Find P(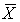 > 73).
> 73).
d. Find P(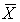 < 74).
< 74).
a. What does the central limit theorem say about the sampling distribution of the sample mean? Why?
b. Find the mean and standard error of the sampling distribution of the sample mean.
c. Find P(
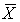 > 73).
> 73).d. Find P(
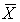 < 74).
< 74).
Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
55
The following table gives the number of pets owned for a population of four families. Find the mean and standard deviation for the population.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
56
An infinite population has a mean of 100 and a standard deviation of 20. Suppose that the population is not normally distributed. What does the central limit theorem say about the sampling distribution of the mean if samples of size 64 are drawn at random from this population?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
57
A sample of size 35 is taken from a normal population, with mean of 65 and standard deviation of 9.3. Describe the sampling distribution of the sample mean.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
58
If a random variable X is not known to be normally distributed, has a mean of size 8 and a variance of size 1.5, describe the sampling distribution of the sample mean for samples of size 30.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
59
In order to estimate the mean salary for a population of 500 employees, the managing director of a certain company selected at random a sample of 40 employees.
a. Would you use the finite population correction factor in calculating the standard error of the sample mean? Explain.
b. If the population standard deviation is $800, compute the standard error both with and without using the finite population correction factor.
c. What is the probability that the sample mean salary of the employees will be within ±$200 of the population mean salary?
a. Would you use the finite population correction factor in calculating the standard error of the sample mean? Explain.
b. If the population standard deviation is $800, compute the standard error both with and without using the finite population correction factor.
c. What is the probability that the sample mean salary of the employees will be within ±$200 of the population mean salary?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
60
In a given year, the average annual salary of an Rugby player was $205 000, with a standard deviation of $24 500. If a simple random sample of 50 players is taken, what is the probability that the sample mean will be less than $210 000?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
61
A video rental store wants to know what proportion of its customers are under 21 years old. A simple random sample of 500 customers is taken, and 350 of them are under 21. Assume that the true population proportion of customers aged under 21 is 0.68.
Describe the sampling distribution of proportion of customers who are under age 21.
Describe the sampling distribution of proportion of customers who are under age 21.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
62
A local newspaper sells an average of 2100 papers per day, with a standard deviation of 500 papers. Consider a sample of 60 days of operation.
a. What is the shape of the sampling distribution of the sample mean number of papers sold per day? Why?
b. Find the expected value and the standard error of the sample mean.
c. What is the probability that the sample mean will be between 2000 and 2300 papers?
a. What is the shape of the sampling distribution of the sample mean number of papers sold per day? Why?
b. Find the expected value and the standard error of the sample mean.
c. What is the probability that the sample mean will be between 2000 and 2300 papers?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
63
A video rental store wants to know what proportion of its customers are under 21 years old. A simple random sample of 500 customers is taken, and 350 of them are under 21. Assume that the true population proportion of customers aged under 21 is 0.68. If another simple random sample of size 500 is taken, what is the probability that more than 70% of customers are under 21 years old?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
64
The following table gives the number of pets owned for a population of four families.  List all possible samples of two families that can be selected without replacement from this population, and compute the sample mean
List all possible samples of two families that can be selected without replacement from this population, and compute the sample mean 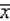 for each sample.
for each sample.
 List all possible samples of two families that can be selected without replacement from this population, and compute the sample mean
List all possible samples of two families that can be selected without replacement from this population, and compute the sample mean 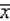 for each sample.
for each sample.
Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
65
Using the following sampling distribution, directly recalculate the mean and standard deviation of 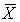 .
. 
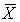 .
. 

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
66
The following table gives the number of pets owned for a population of four families. Samples of size 2 will be drawn at random from the population. Use your answers to the previous question to calculate the mean and the standard deviation of the sampling distribution of the sample means.

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
67
A video rental store wants to know what proportion of its customers are under 21 years old. A simple random sample of 500 customers is taken, and 375 of them are under 21. Assume that the true population proportion of customers aged under 21 is 0.68.
What is the probability that the sample proportion will be within 0.03 of the true proportion of customers who are aged under 21?
What is the probability that the sample proportion will be within 0.03 of the true proportion of customers who are aged under 21?

Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck
68
The following table gives the number of pets owned for a population of four families.  Find the sampling distribution of
Find the sampling distribution of 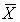 .
.
 Find the sampling distribution of
Find the sampling distribution of 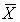 .
.
Unlock Deck
Unlock for access to all 68 flashcards in this deck.
Unlock Deck
k this deck


