Deck 8: Using the Definite Integral
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/104
Play
Full screen (f)
Deck 8: Using the Definite Integral
1
You love the function 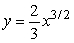 and you also love the number 6.What is the arc length of this curve from x = 0 to x = 6? Round to 2 decimal places.
and you also love the number 6.What is the arc length of this curve from x = 0 to x = 6? Round to 2 decimal places.
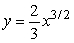 and you also love the number 6.What is the arc length of this curve from x = 0 to x = 6? Round to 2 decimal places.
and you also love the number 6.What is the arc length of this curve from x = 0 to x = 6? Round to 2 decimal places.The arc length is about 11.68 units.
2
A large chocolate bar has trapezoidal cross section shown in the following figure.If you want the bar to have volume 861 cm3, what should H be? 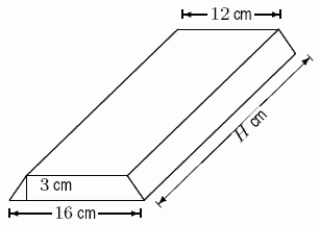

20.5
3
Focus on Engineering It's time for the School of Engineering class picture and you are the photographer! You stand at the origin with your camera and your classmates are strung out along the curve from (0, 1)to .You focus your camera at the average value of the distance to your classmates on the curve.Who is more in focus, the person at (0, 1)or the person at ? 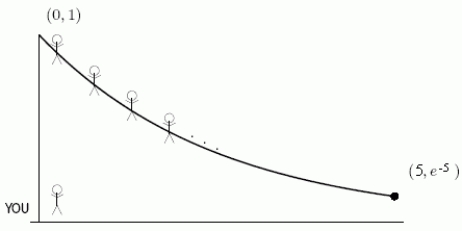
A)The person at (0, 1).
B)The person at .

A)The person at (0, 1).
B)The person at .
The person at (0, 1).
4
Suppose that a new office building is being planned.The architect wants to design a building that is thick at the base and eventually tapers to a small flat roof at the top.The building is to have 10 floors, and each floor is to be 15 feet high.For purposes of air conditioning the building, an estimate of the total volume is needed.You have been hired as a consultant at an exorbitant salary to do this.You have been provided with the following information which shows how much area, in units of 100 square feet, each of the 10 floors will contain:
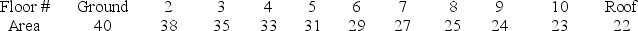
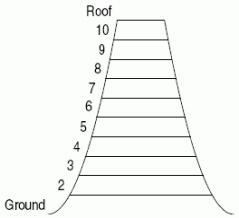 Earn your wage: find an approximate value for the number of cubic feet in the entire building.
Earn your wage: find an approximate value for the number of cubic feet in the entire building.
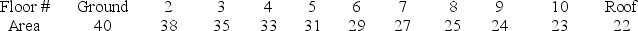
 Earn your wage: find an approximate value for the number of cubic feet in the entire building.
Earn your wage: find an approximate value for the number of cubic feet in the entire building.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
5
A coffee filter is in the shape of a cone, as shown below.Suppose that when it is filled with water to a height h cm, the rate at which coffee flows out the hole at the bottom is given by
Volume of coffee which flows out per second =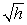 cm3 / sec.
cm3 / sec. 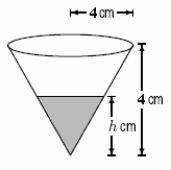 Suppose the coffee filter starts full.Write an integral representing the total amount of time it takes for the coffee filter to empty, and then evaluate it to find the time needed for the filter to empty.Give your answer to the nearest second.
Suppose the coffee filter starts full.Write an integral representing the total amount of time it takes for the coffee filter to empty, and then evaluate it to find the time needed for the filter to empty.Give your answer to the nearest second.
Volume of coffee which flows out per second =
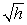 cm3 / sec.
cm3 / sec.  Suppose the coffee filter starts full.Write an integral representing the total amount of time it takes for the coffee filter to empty, and then evaluate it to find the time needed for the filter to empty.Give your answer to the nearest second.
Suppose the coffee filter starts full.Write an integral representing the total amount of time it takes for the coffee filter to empty, and then evaluate it to find the time needed for the filter to empty.Give your answer to the nearest second.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
6
In a recent archaeological expedition, a scroll was discovered containing a description of a plan to build what appears to be the Tower of Babel.According to the manuscript, the tower was supposed to have a circular cross section and "go up to the heavens" (i.e., be infinitely high).A mathematician was consulted to solve some of the questions posed by the archaeologists.The mathematicians plotted half of the silhouette of the tower on a set of coordinate axes with the y-axis running through the center and discovered that it was approximated by the curve .The manuscript mentions that 2560 cubic "shrims" (Babel's unit of length)of stones were available to build the tower.The base of the tower was to have radius 3 shrims.Did they have enough?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
7
Focus on Engineering It's time for the School of Engineering class picture and you are the photographer! You stand at the origin with your camera and your classmates are strung out along the curve from (0, 1)to . 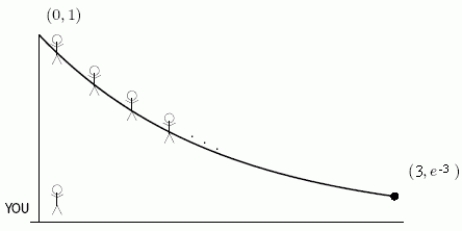 What is the formula for the average value of the distance from you to your classmates at points (x, y)on the curve?
What is the formula for the average value of the distance from you to your classmates at points (x, y)on the curve?
A)
B)
C)
D)
 What is the formula for the average value of the distance from you to your classmates at points (x, y)on the curve?
What is the formula for the average value of the distance from you to your classmates at points (x, y)on the curve?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
8
A rectangular lake is 100 km long and 60 km wide.The depth of the water at any point of the surface is a tenth of the distance from the nearest shoreline.How many km3 of water does the lake contain? Round to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
9
A cone has base radius = 4 cm and height = 2 cm.Using horizontal slicing, which of the following definite integrals represents volume of the cone?
A) cm3
B) cm3
C) cm3
D) cm3
A) cm3
B) cm3
C) cm3
D) cm3

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
10
In a recent archaeological expedition, a scroll was discovered containing a description of a plan to build what appears to be the Tower of Babel.According to the manuscript, the tower was supposed to have a circular cross section and "go up to the heavens" (i.e., be infinitely high).A mathematician was consulted to solve some of the questions posed by the archaeologists.The mathematicians plotted half of the silhouette of the tower on a set of coordinate axes with the y-axis running through the center and discovered that it was approximated by the curve 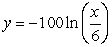 .Would such a tower have finite volume? If so, calculate it to the nearest whole number.If not, enter "infinite".
.Would such a tower have finite volume? If so, calculate it to the nearest whole number.If not, enter "infinite".
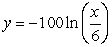 .Would such a tower have finite volume? If so, calculate it to the nearest whole number.If not, enter "infinite".
.Would such a tower have finite volume? If so, calculate it to the nearest whole number.If not, enter "infinite".
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
11
Find the area of the dumbbell shaped region bounded by the curve 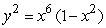 .Round your answer to 2 decimal places.
.Round your answer to 2 decimal places.
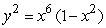 .Round your answer to 2 decimal places.
.Round your answer to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
12
Focus on Engineering
It's time for the School of Engineering class picture and you are the photographer! You stand at the origin with your camera and your classmates are strung out along the curve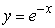 from (0, 1)to
from (0, 1)to 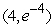 .
. 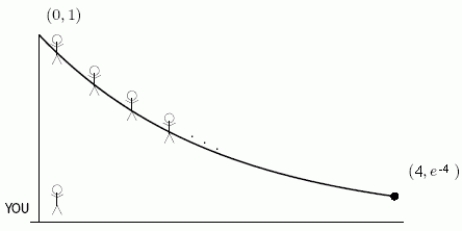 Use a calculator to find the average value of the distance from you to your classmates at a point (x, y)on the curve.Round to 3 decimal places.
Use a calculator to find the average value of the distance from you to your classmates at a point (x, y)on the curve.Round to 3 decimal places.
It's time for the School of Engineering class picture and you are the photographer! You stand at the origin with your camera and your classmates are strung out along the curve
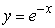 from (0, 1)to
from (0, 1)to 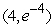 .
.  Use a calculator to find the average value of the distance from you to your classmates at a point (x, y)on the curve.Round to 3 decimal places.
Use a calculator to find the average value of the distance from you to your classmates at a point (x, y)on the curve.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
13
If a cylinder has radius 6 and height h (in centimeters), which of the following definite integrals represents the volume using slices?
A) cm3
B) cm3
C) cm3
D) cm3
A) cm3
B) cm3
C) cm3
D) cm3

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the region bounded by 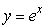 , the x-axis and the lines x = 0 and x = 2.Find the volume of the solid whose base is the given region and whose cross sections perpendicular to the x-axis are isosceles right triangles with hypotenuses lying in the region.Round to 2 decimal places.
, the x-axis and the lines x = 0 and x = 2.Find the volume of the solid whose base is the given region and whose cross sections perpendicular to the x-axis are isosceles right triangles with hypotenuses lying in the region.Round to 2 decimal places.
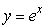 , the x-axis and the lines x = 0 and x = 2.Find the volume of the solid whose base is the given region and whose cross sections perpendicular to the x-axis are isosceles right triangles with hypotenuses lying in the region.Round to 2 decimal places.
, the x-axis and the lines x = 0 and x = 2.Find the volume of the solid whose base is the given region and whose cross sections perpendicular to the x-axis are isosceles right triangles with hypotenuses lying in the region.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
15
Alice starts at the origin and walks along the graph of at a velocity of 6 units/second.Which of the following integrals show how far Alice has traveled when she reaches the point where x = a?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
16
Alice starts at the origin and walks along the graph of 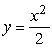 at a velocity of 11 units/second.You want to find the x-coordinate of the point Alice reaches after traveling for 2 seconds.Estimate this coordinate to 1 decimal place.
at a velocity of 11 units/second.You want to find the x-coordinate of the point Alice reaches after traveling for 2 seconds.Estimate this coordinate to 1 decimal place.
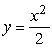 at a velocity of 11 units/second.You want to find the x-coordinate of the point Alice reaches after traveling for 2 seconds.Estimate this coordinate to 1 decimal place.
at a velocity of 11 units/second.You want to find the x-coordinate of the point Alice reaches after traveling for 2 seconds.Estimate this coordinate to 1 decimal place.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
17
A coffee filter is in the shape of a cone, as shown below.Suppose that when it is filled with water to a height h cm, the rate at which coffee flows out the hole at the bottom is given by Volume of coffee which flows out per second = cm3 / sec. 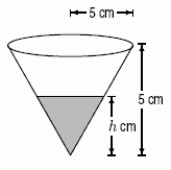 Approximately how many cubic centimeters are in the "slice" of coffee lying below h + h and above h?
Approximately how many cubic centimeters are in the "slice" of coffee lying below h + h and above h?
A)
B)
C)
D)
 Approximately how many cubic centimeters are in the "slice" of coffee lying below h + h and above h?
Approximately how many cubic centimeters are in the "slice" of coffee lying below h + h and above h?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following integrals determines the volume of a cone of height H and radius R?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
19
What is represented by the integral ?
A)A cone with radius 6 and height 6.
B)A cone with radius 3 and height 6.
C)A sphere with radius 6.
D)A hemisphere with radius 6.
A)A cone with radius 6 and height 6.
B)A cone with radius 3 and height 6.
C)A sphere with radius 6.
D)A hemisphere with radius 6.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
20
What is represented by the integral ?
A)A cone with radius 2 and height 4.
B)A cone with radius 4 and height 4.
C)A sphere with radius 4.
D)A hemisphere with radius 4.
A)A cone with radius 2 and height 4.
B)A cone with radius 4 and height 4.
C)A sphere with radius 4.
D)A hemisphere with radius 4.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
21
A curve is given parametrically as and for 0 t 2 .How does the length change if the coefficients of x and y are doubled (meaning x = 8 sin t and y = 8 cos t)?
A)The length is doubled.
B)The length is halved
C)The length is increased by a factor of 4.
D)The length remains the same.
A)The length is doubled.
B)The length is halved
C)The length is increased by a factor of 4.
D)The length remains the same.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
22
A thin strip of nutrients 20 cm long is placed in a circular petri dish of radius 10 cm, as shown.The population density of bacteria in the disk after 3 hours is given by bacteria/cm2 where D is the distance (in cm)to the nutrient strip.Which of the following integrals gives the number of bacteria in the petri dish 3 hours after the nutrient strip has been introduced? 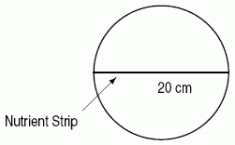
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
23
A cylindrically-shaped mug with a 3cm radius and a 10cm height is filled with tea.You have added some sugar to the tea, which tends to settle to the bottom of the mug.It turns out that the density of sugar (in gm/cm3)in the tea, as a function of the height, h, in cm, above the bottom of the mug, is given by the formula (h)= 0.025(10 - h).Which of the following Riemann sums approximates the total mass of sugar (in grams)in the mug of tea? 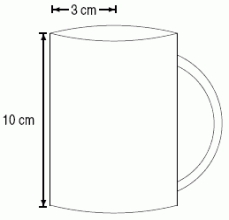
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
24
A plastic travel mug is made in two parts, the cup and the base.The cup part has outside shape 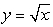 and inside shape
and inside shape 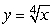 cut off at x = 4 as shown in the following figure.
cut off at x = 4 as shown in the following figure. 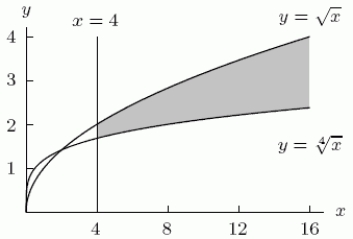 If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.
If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.
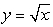 and inside shape
and inside shape 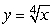 cut off at x = 4 as shown in the following figure.
cut off at x = 4 as shown in the following figure.  If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.
If the cup is 14 cm tall, and the base is 10 cm in diameter and 1 cm thick, find the volume of plastic needed to make the mug.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
25
Choose inequalities for r and which describe the following region in polar coordinates. 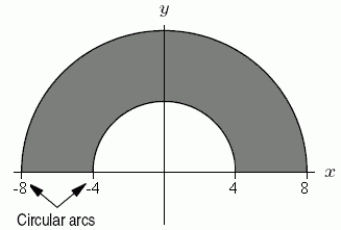
A) and
B) and
C) and
D) and

A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
26
Find the length of the curve given parametrically as and for 0 t 2 .Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
27
A straight road goes through the center of a circular city of radius 5 km.The density of the population at a distance r (in km)from the road is well approximated by 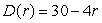 (in thousand people per km2).Find the total population of the city, to the nearest person.
(in thousand people per km2).Find the total population of the city, to the nearest person.
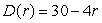 (in thousand people per km2).Find the total population of the city, to the nearest person.
(in thousand people per km2).Find the total population of the city, to the nearest person.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
28
Find the area outside the limaçon r = 1 + cos and inside the circle r = 2.Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
29
When an oil well burns, sediment is carried up into the air by the flames and is eventually deposited on the ground.Less sediment is deposited further away from the oil well.Suppose that the density (in tons/square mile)at a distance r from the burning oil well is given by .Which Riemann sum approximates the total amount of sediment which is deposited within 100 miles of the well?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
30
Find the volume of the solid obtained by rotating the region bounded by 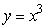 , x = 0, y = 0, and y = -8 around y = 1.Round to 2 decimal places.
, x = 0, y = 0, and y = -8 around y = 1.Round to 2 decimal places.
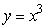 , x = 0, y = 0, and y = -8 around y = 1.Round to 2 decimal places.
, x = 0, y = 0, and y = -8 around y = 1.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
31
A cylindrically-shaped mug with a 3 cm radius and a 10 cm height is filled with tea.You have added some sugar to the tea, which tends to settle to the bottom of the mug.It turns out that the density of sugar (in gm/cm3)in the tea, as a function of the height, h, in cm, above the bottom of the mug, is given by the formula (h)= 0.01(10 - h).Find the amount of sugar in the mug.Round to 2 decimal places. 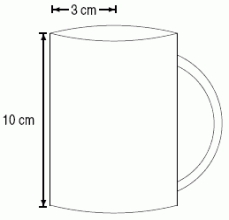


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
32
The globular cluster M13 is a spherical distribution of stars which orbits our galaxy.Suppose that the density of stars in the cluster is purely a function of distance r from the center of the cluster and is given as stars/(ly)3, where r is measured in light-years, and 0 r 90 ly.(One light-year is the distance light travels in one year; "light-year" is abbreviated as "ly".)Find the number of stars in M13.Round to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
33
The globular cluster M13 is a spherical distribution of stars which orbits our galaxy.Suppose that the density of stars in the cluster is purely a function of distance r from the center of the cluster and is given as stars/(ly)3, where r is measured in light-years, and 0 r 120 ly.(One light-year is the distance light travels in one year; "light-year" is abbreviated as "ly".)Set up an integral whose value is the exact number of stars in M13.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
34
Find the area inside the three-petal rose 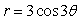 shown in the following figure.Round to 2 decimal places.
shown in the following figure.Round to 2 decimal places. 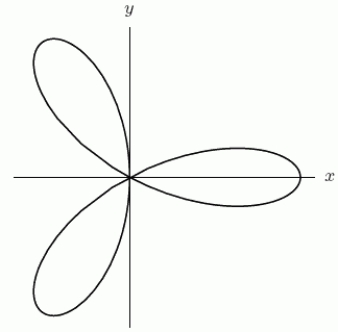
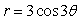 shown in the following figure.Round to 2 decimal places.
shown in the following figure.Round to 2 decimal places. 

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
35
Set up an integral representing the volume of the torus (donut)obtained by rotating the circle about the y-axis.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
36
When an oil well burns, sediment is carried up into the air by the flames and is eventually deposited on the ground.Less sediment is deposited further away from the oil well.Suppose that the density (in tons/square mile)at a distance r from the burning oil well is given by 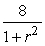 .Find and evaluate an integral which represents the total amount of sediment which is deposited within 100 miles of the well.Round to 2 decimal places.
.Find and evaluate an integral which represents the total amount of sediment which is deposited within 100 miles of the well.Round to 2 decimal places.
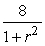 .Find and evaluate an integral which represents the total amount of sediment which is deposited within 100 miles of the well.Round to 2 decimal places.
.Find and evaluate an integral which represents the total amount of sediment which is deposited within 100 miles of the well.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
37
Find the arc length of 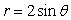 ,
, 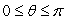 .Give an exact answer and then round to 2 decimal places.
.Give an exact answer and then round to 2 decimal places.
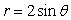 ,
, 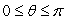 .Give an exact answer and then round to 2 decimal places.
.Give an exact answer and then round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
38
Set up a Riemann sum approximating the volume of the torus (donut)obtained by rotating the circle about the y-axis.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
39
The circle 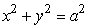 is rotated around the y-axis to form a solid sphere of radius a.A plane perpendicular to the y-axis at y = a/5 cuts off a spherical cap from the sphere.What percent of the total volume of the sphere is contained in the cap? Round to 2 decimal places.
is rotated around the y-axis to form a solid sphere of radius a.A plane perpendicular to the y-axis at y = a/5 cuts off a spherical cap from the sphere.What percent of the total volume of the sphere is contained in the cap? Round to 2 decimal places.
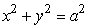 is rotated around the y-axis to form a solid sphere of radius a.A plane perpendicular to the y-axis at y = a/5 cuts off a spherical cap from the sphere.What percent of the total volume of the sphere is contained in the cap? Round to 2 decimal places.
is rotated around the y-axis to form a solid sphere of radius a.A plane perpendicular to the y-axis at y = a/5 cuts off a spherical cap from the sphere.What percent of the total volume of the sphere is contained in the cap? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
40
After Mt.St.Helens erupted in 1980, it was found that ash was spread in decreasing density as a function of distance r from the center of the crater.Say that the density of ash at a distance r (meters)from the center of the crater is given by kg/m2.Find the total amount of ash within 1400 meters of the center of the crater.Round to the nearest whole number and give your answer in kg.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
41
A study of the costs to produce airplanes in World War II led to the theory of "learning curves," the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the xth plane is given by ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.](https://storage.examlex.com/TB4204/11eb1831_d919_734d_88c1_cbbcf59398a9_TB4204_11.jpg) , where
, where ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.](https://storage.examlex.com/TB4204/11eb1831_d919_734e_88c1_f1591ba359ab_TB4204_11.jpg) = marginal cost to produce the first plane.[Note: You may use the fact that
= marginal cost to produce the first plane.[Note: You may use the fact that ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.](https://storage.examlex.com/TB4204/11eb1831_d919_734f_88c1_077b4747af80_TB4204_11.jpg) .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.
.] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.
![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.](https://storage.examlex.com/TB4204/11eb1831_d919_734d_88c1_cbbcf59398a9_TB4204_11.jpg) , where
, where ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.](https://storage.examlex.com/TB4204/11eb1831_d919_734e_88c1_f1591ba359ab_TB4204_11.jpg) = marginal cost to produce the first plane.[Note: You may use the fact that
= marginal cost to produce the first plane.[Note: You may use the fact that ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.](https://storage.examlex.com/TB4204/11eb1831_d919_734f_88c1_077b4747af80_TB4204_11.jpg) .] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.
.] If a plant produces planes with a 90% learning curve on production costs, and the marginal cost for the first plane is $700,000, then what is the marginal cost to produce the fourth plane? Round to the nearest thousand dollars.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
42
An object is in the shape drawn below; its boundary is obtained by rotating the parabola (for 0 x 1)around the y axis.(Units are in centimeters.)Suppose that the density of this object varies with height according to the rule (y)= 12 (2 - y)grams/cm3.Which of the following Riemann sums computes (approximately)the mass in grams of this object? 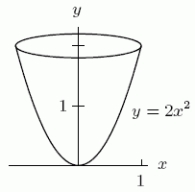
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
43
The work done lifting a 5-lb bag of sugar 4 feet off the floor is _____ ft-lbs.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
44
If it is known to take 147 joules of work to lift a box 1.5 meters off the floor, what is the mass of the box in kg?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
45
A swimming pool has shape as shown in the following figure. 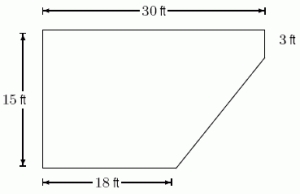 If the pool is 9 ft deep, how many foot-pounds does it take to pump all the water out? (Note: water weighs 62.4 pounds/ft3.)Round to the nearest whole number.
If the pool is 9 ft deep, how many foot-pounds does it take to pump all the water out? (Note: water weighs 62.4 pounds/ft3.)Round to the nearest whole number.
 If the pool is 9 ft deep, how many foot-pounds does it take to pump all the water out? (Note: water weighs 62.4 pounds/ft3.)Round to the nearest whole number.
If the pool is 9 ft deep, how many foot-pounds does it take to pump all the water out? (Note: water weighs 62.4 pounds/ft3.)Round to the nearest whole number.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
46
The density of cars (in cars per mile)down a 24-mile stretch of the Massachusetts Turnpike starting at a toll plaza is given by , where x is the distance in miles from the toll plaza and 0 x 24.Estimate the total number of cars down the 24-mile stretch by creating a Reimann sum, converting it to an integral, and evaluating it.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
47
A bridge worker needs to pull a 14-meter uniform cable with mass 3 kg/meter up to the work platform.How many joules are needed, assuming that the cable is hanging straight down from the platform? Round to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
48
Circle City is circular with a radius of 3 miles.Right in the center is a circular park with radius one mile.No one lives in the park.Elsewhere the population density is 3000(5 - r)people per square mile, where r is the distance from the center in miles.What is the total population of Circle City, to the nearest thousand?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
49
A flat metal plate is in the shape determined by the area under the graph of 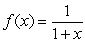 between x = 0 and x = 4.The density of the plate x units from the y-axis is given by x2 grams/cm2.Write down a Riemann sum which approximates the total mass.Convert it to an integral, and evaluate the integral to 3 decimal places.
between x = 0 and x = 4.The density of the plate x units from the y-axis is given by x2 grams/cm2.Write down a Riemann sum which approximates the total mass.Convert it to an integral, and evaluate the integral to 3 decimal places. 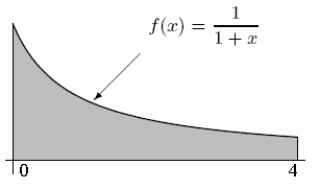
 between x = 0 and x = 4.The density of the plate x units from the y-axis is given by x2 grams/cm2.Write down a Riemann sum which approximates the total mass.Convert it to an integral, and evaluate the integral to 3 decimal places.
between x = 0 and x = 4.The density of the plate x units from the y-axis is given by x2 grams/cm2.Write down a Riemann sum which approximates the total mass.Convert it to an integral, and evaluate the integral to 3 decimal places. 

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
50
A study of the costs to produce airplanes in World War II led to the theory of "learning curves," the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the xth plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).What, physically, is the meaning of the constant of integration in your formula?
A)The cost of producing the first plane.
B)The cost if no planes are produced (the cost of setting up the plant for production).
C)The marginal cost of the xth unit.
D)The average cost of producing x units.
A)The cost of producing the first plane.
B)The cost if no planes are produced (the cost of setting up the plant for production).
C)The marginal cost of the xth unit.
D)The average cost of producing x units.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
51
The force of gravitational attraction between a thin rod of mass M and length L and a particle of mass m lying on the same line as the rod at a distance of A from one of the ends is .Use this result to select an integral for the total force due to gravity between two thin rods, both of mass M and length L, lying along the same line and separated by a distance A.[Hint: Divide one of the rods into small pieces, each of length dx and mass .Apply the formula above to each of the pieces, then form a Riemann sum.You know the rest…] ![<strong>The force of gravitational attraction between a thin rod of mass M and length L and a particle of mass m lying on the same line as the rod at a distance of A from one of the ends is \frac{G m M}{A(L+A)} .Use this result to select an integral for the total force due to gravity between two thin rods, both of mass M and length L, lying along the same line and separated by a distance A.[Hint: Divide one of the rods into small pieces, each of length dx and mass \frac{M}{L} d x .Apply the formula above to each of the pieces, then form a Riemann sum.You know the rest…] </strong> A) F=\int_{A}^{A+L} \frac{G M^{2} d x}{L x(L+x)} B) F=\int_{A}^{A+L} \frac{G M^{2} d x}{x(L+x)} C) F=\int_{0}^{A} \frac{G M^{2} d x}{L(L+x)} D) F=\int_{0}^{A} \frac{G M^{2} d x}{x(L+x)}](https://storage.examlex.com/TB4204/11eb1831_d918_88e7_88c1_590a7e89f2b1_TB4204_00.jpg)
A)
B)
C)
D)
![<strong>The force of gravitational attraction between a thin rod of mass M and length L and a particle of mass m lying on the same line as the rod at a distance of A from one of the ends is \frac{G m M}{A(L+A)} .Use this result to select an integral for the total force due to gravity between two thin rods, both of mass M and length L, lying along the same line and separated by a distance A.[Hint: Divide one of the rods into small pieces, each of length dx and mass \frac{M}{L} d x .Apply the formula above to each of the pieces, then form a Riemann sum.You know the rest…] </strong> A) F=\int_{A}^{A+L} \frac{G M^{2} d x}{L x(L+x)} B) F=\int_{A}^{A+L} \frac{G M^{2} d x}{x(L+x)} C) F=\int_{0}^{A} \frac{G M^{2} d x}{L(L+x)} D) F=\int_{0}^{A} \frac{G M^{2} d x}{x(L+x)}](https://storage.examlex.com/TB4204/11eb1831_d918_88e7_88c1_590a7e89f2b1_TB4204_00.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
52
An object is in the shape drawn below; its boundary is obtained by rotating the parabola (for 0 x 1)around the y axis.(Units are in centimeters.)Suppose that the density of this object varies with height according to the rule (y)= 8 (2 - y)grams/cm3.Compute the mass in grams of this object.Give an exact answer and then round it to 2 decimal places. 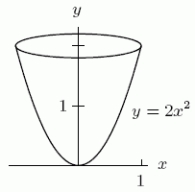


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
53
A 3-gram drop of thick red paint is added to a large can of white paint.A red disk forms and spreads outward, growing lighter at the edges.Since the amount of red paint stays constant through time, the density of the red paint in the disk must vary with time.Suppose that its density p in gm/cm2 is of the form for some functions k(t)of time and f(r)of the distance to the center of the disk.Let R(t)be the radius of the disk at time t.Which of the following equations expresses the fact that there are 3 grams of red paint in the disk?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
54
The Great Cone of Haverford College is a monument built by freshmen during a customs week long, long ago.It is 100 ft.high and its base has a diameter of 100 ft.It has been built from bricks (purportedly made of straw)which weigh 2 lbs/ft3.Use a definite integral to approximate the number of foot-pounds required to build the Cone.Round to the nearest million. 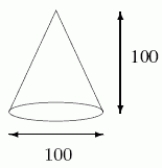


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
55
The density of cars (in cars per mile)down a 20-mile stretch of the Massachusetts Turnpike starting at a toll plaza is given by , where x is the distance in miles from the toll plaza and 0 x 20.Which of the following Riemann sums estimates the total number of cars down the 20-mile stretch?
A) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
B) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
C) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
D) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
A) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
B) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
C) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.
D) , where the 20-mile stretch is divided into n pieces of length , and
is a point in the i th segment.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
56
Circle City is circular with a radius of 3 miles.Right in the center is a circular park with radius one mile.No one lives in the park.Elsewhere the population density is 4500(5 - r)people per square mile, where r is the distance from the center in miles.What is the average population density of Circle City, to the nearest whole number?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
57
A 5-gram drop of thick red paint is added to a large can of white paint.A red disk forms and spreads outward, growing lighter at the edges.Since the amount of red paint stays constant through time, the density of the red paint in the disk must vary with time.Suppose that its density p in gm/cm2 is of the form for some functions k(t)of time and f(r)of the distance to the center of the disk.For fixed r, which of the following integrals gives the average density of red paint at a distance r from the center of the disk from 0 to T seconds?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
58
A chlorine solution is poured over the surface of a rectangular swimming pool that is 20 meters long, 10 meters wide and 2 meters deep everywhere.Before the circulating pumps in the pool are turned on, it is discovered that the density of the chlorine solution at a height h meters above the bottom of the pool is given by (h)= 100h grams/m3. In other words, the chlorine solution has distributed itself so that its density increases linearly from the bottom of the pool.Write a Riemann sum that approximates the total mass of chlorine solution in the pool, convert it into a definite integral, and evaluate it to find the total mass of the chlorine solution in the pool.Give your answer in kg.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
59
A bridge worker needs to pull a 10-meter uniform cable with mass 3 kg/meter up to the work platform.A second worker needs to pull an identical cable (which is one-half as long)up one-half the original distance.Will the second worker do one-half the work of the first worker? Assume that each cable is hanging straight down from its platform.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
60
The density of a compressible liquid is 30(5 - h)kg/m3 at a height of h meters above the bottom.The liquid is put in the container as shown below (resting on the triangular side).The cross sections of the container are isosceles triangles, it has straight sides, and it looks like a triangular prism.How many kg will it hold? Round to the nearest whole number. 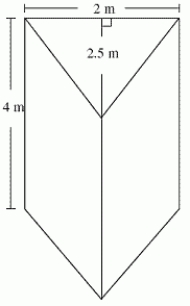


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
61
On each of two days (January 1, 2005 and January 1, 2006), a person deposits $2500 in a savings bank.The bank deposits interest in the account at a rate of 6%, compounded 4 times per year.Choose the sum that gives the size of the bank account at the end of 2006.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
62
By the year 2016 you will have made your first million dollars.You invest it in a new company on January 1, 2017.The new company starts to earn a profit six months later.Thus, starting July 1, 2017, you receive income from the company in a continuous stream at a constant rate of 1/2 million dollars per year. Your bank offers interest at a nominal rate of 8% per year, compounded continuously.Consider the date when will you have received an income of $1 million from the company.(Do not take into account the bank's interest; this question is simply asking when the total income you have received will reach $1 million.)Which of the following is true?
A)Your investment paid off on that date.
B)Your investment paid off before that date
C)Your investment will not be paid off until after that date
A)Your investment paid off on that date.
B)Your investment paid off before that date
C)Your investment will not be paid off until after that date

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
63
The capital value of an asset such as a machine is sometimes defined as the present value of all future net earnings of the asset.The actual lifetime of the asset may not be known, and since some assets last indefinitely, the capital value of the asset may be written in the form 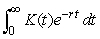 ,
,
where K(t)is the annual rate of earnings produced by the asset at time t, and r is the annual interest rate, compounded continuously.Find the capital value of an asset that generates income at a rate of $1000 per year, with an interest rate of 9%.Round to the nearest dollar.
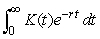 ,
,where K(t)is the annual rate of earnings produced by the asset at time t, and r is the annual interest rate, compounded continuously.Find the capital value of an asset that generates income at a rate of $1000 per year, with an interest rate of 9%.Round to the nearest dollar.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
64
The probability density function f(x)shown below describes the chances that a computer circuit board will cost a manufacturer more than a certain number of dollars to produce.In this case, the cost of the circuit board, x, is measured in thousands of dollars.What is the probability that the circuit board will cost less than $2 thousand to produce? 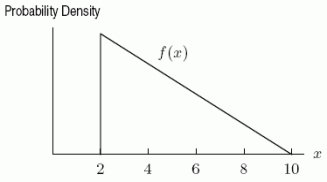


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
65
The probability density function f(x)shown below describes the chances that a computer circuit board will cost a manufacturer more than a certain number of dollars to produce.In this case, the cost of the circuit board, x, is measured in thousands of dollars.Which of the following definite integrals give the probability that the circuit card will cost between $2 thousand and some amount $b thousand? Assume that b is between 2 and 10. 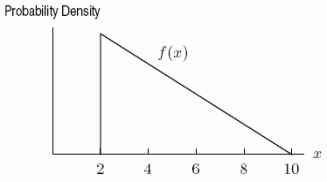
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
66
You have $100,000 that you want to invest.Some "business men" are willing to sell you a machine for your $100,000 that prints money.You figure that every day you can print $200 with the machine, and you would deposit the $200 each day in a "special" bank account at BCCI.Your friends at BCCI will only be able to offer you 5% nominal annual interest, compounded continuously, due to the "sensitive nature" of the transaction.It would be your intention to print money each day for one year.If you were depositing the money that you printed in a continuous stream at a constant rate of $200 per day into the bank account, then find and evaluate a definite integral that gives your balance after one year.Round to the nearest dollar.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
67
It is estimated that in fifteen years, it will cost $200,000 to send a child to a four-year college.Suppose you want to set up an account at a bank that offers 8% nominal annual interest compounded continuously, so that 20 years from today, the account has $200,000 in it for your child's college education.Determine at what constant continuous rate K dollars per year you would need to deposit money as follows:
Set up a differential equation for the rate of change of your bank balance, where B = f(t)is your bank balance at time t.Next, solve this differential equation for an initial balance of zero.Finally, use this result find K (to the nearest dollar).
Set up a differential equation for the rate of change of your bank balance, where B = f(t)is your bank balance at time t.Next, solve this differential equation for an initial balance of zero.Finally, use this result find K (to the nearest dollar).

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
68
By the year 2016 you will have made your first million dollars.You invest it in a new company on January 1, 2017.The new company starts to earn a profit six months later.Thus, starting July 1, 2017, you receive income from the company in a continuous stream at a constant rate of 1/2 million dollars per year. Your bank offers interest at a nominal rate of 8% per year, compounded continuously.When will you have received an income of $1 million from the company? (Do not take into account the bank's interest; this question is simply asking when the total income you have received will reach $1 million.)
A)July 1, 2019
B)January 1, 2019
C)July1, 2018
D)January1, 2018
A)July 1, 2019
B)January 1, 2019
C)July1, 2018
D)January1, 2018

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
69
Somebody offers to pay you money in one of the following ways: • Two $50 payments, one six months from now and one twelve months from now.
• Payment in a continuous cash flow over the next year at a constant rate of $99 per year.
These payments are to be deposited into a bank account that earns 10% interest compounded continuously.You want to determine which plan is preferable, i.e., which plan has a larger present value.Find the present value of the first payment plan.Then use a Riemann sum converted into a definite integral to get the exact present value of the second payment plan.Which payment plan has the larger present value?
A)The second one
B)The first one
• Payment in a continuous cash flow over the next year at a constant rate of $99 per year.
These payments are to be deposited into a bank account that earns 10% interest compounded continuously.You want to determine which plan is preferable, i.e., which plan has a larger present value.Find the present value of the first payment plan.Then use a Riemann sum converted into a definite integral to get the exact present value of the second payment plan.Which payment plan has the larger present value?
A)The second one
B)The first one

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
70
You have $100,000 that you want to invest.Some "business men" are willing to sell you a machine for your $100,000 that prints money.You figure that every day you can print $200 with the machine, and you would deposit the $200 each day in a "special" bank account at BCCI.Your friends at BCCI will only be able to offer you 5% nominal annual interest, compounded continuously, due to the "sensitive nature" of the transaction.It would be your intention to print money each day for one year.Which of the following sums gives the value of your bank balance after one year?
A) , with day
B) , with day
C)
, with day
D) , with day
A) , with day
B) , with day
C)
, with day
D) , with day

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
71
By the year 2016 you will have made your first million dollars.You invest it in a new company on January 1, 2017.The new company starts to earn a profit six months later.Thus, starting July 1, 2017, you receive income from the company in a continuous stream at a constant rate of 1/2 million dollars per year.
Your bank offers interest at a nominal rate of 6% per year, compounded continuously.Suppose T is measured in years from January 1, 2017.Compute the future value of your original investment of $1 million at time T and the future value at time T of the income that you have received by that time.Use these to determine how many years, T, it will take for your investment to have paid off.Round to 2 decimal places.
Your bank offers interest at a nominal rate of 6% per year, compounded continuously.Suppose T is measured in years from January 1, 2017.Compute the future value of your original investment of $1 million at time T and the future value at time T of the income that you have received by that time.Use these to determine how many years, T, it will take for your investment to have paid off.Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
72
The probability density function f(x)shown below describes the chances that a computer circuit board will cost a manufacturer more than a certain number of dollars to produce.In this case, the cost of the circuit board, x, is measured in thousands of dollars.Find the height of the triangle that describes the probability density function. 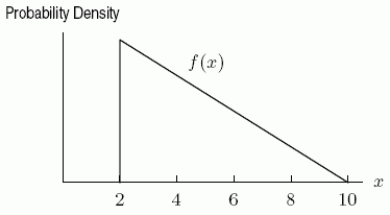


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
73
You have a bank account that earns 9% nominal annual interest compounded continuously, and you want to have $90,000 in the bank account in five years so that you can buy a brand new Porsche.How much money would you have to deposit in one lump sum today so that the account balance would be $90,000 in five years? Round to the nearest dollar.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
74
An insurance salesman offers you a life insurance policy with the following terms.You are to make payments at a rate of $1000 per year until age 70.If you pass away at any time, the policy will pay $150,000.Consider the payments to be made at a constant continuous rate of $1000 per year.You are 30 years old, and you have a bank account that you know will offer you 5% nominal annual interest compounded continuously for an indefinite amount of time.You could choose instead to make the $1000 payments into your bank account instead of paying for the insurance policy. If you stop these payments at age 70, just as you would stop making payments on the life insurance policy, then you would simply earn interest on the bank balance that you have accumulated to that point.If you feel that you are likely to live to be 76 years old, which is the better option?
A)The insurance policy
B)The bank account
A)The insurance policy
B)The bank account

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
75
AnsYou have $100,000 that you want to invest.Some "business men" are willing to sell you a machine for your $100,000 that prints money.You figure that every day you can print $310 with the machine, and you would deposit the $310 each day in a "special" bank account at BCCI.Your friends at BCCI will only be able to offer you 5% nominal annual interest, compounded continuously, due to the "sensitive nature" of the transaction.It would be your intention to print money each day for one year.If you were depositing the money that you printed in a continuous stream at a constant rate of $310 per day into the bank account, then find and evaluate a definite integral that gives your balance after one year.If you had just taken the original $100,000 and placed it in a regular bank account that compounds interest annually, then what interest rate would you have had to earn in order for this option to be more profitable than the money machine (legal concerns aside)? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
76
A lightbulb company is interested in the lifespan of their lightbulbs.They have 20,000 lightbulbs burning and have collected the following information.
After 2 months, 98% of the bulbs were still working.
After 8 months, 80% of the bulbs were still working.
We summarize all the data collected below: (Read carefully: the data was not collected at regular intervals.)
 Approximate the average lifespan of a lightbulb in months.Round to 2 decimal places.
Approximate the average lifespan of a lightbulb in months.Round to 2 decimal places.
After 2 months, 98% of the bulbs were still working.
After 8 months, 80% of the bulbs were still working.
We summarize all the data collected below: (Read carefully: the data was not collected at regular intervals.)
 Approximate the average lifespan of a lightbulb in months.Round to 2 decimal places.
Approximate the average lifespan of a lightbulb in months.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
77
A lightbulb company is interested in the lifespan of their lightbulbs.They have 20,000 lightbulbs burning and have collected the following information.
After 2 months, 98% of the bulbs were still working.
After 8 months, 80% of the bulbs were still working.
We summarize all the data collected below: (Read carefully: the data was not collected at regular intervals.)
 How many bulbs out of the original 20,000 burned out during the first 4 months?
How many bulbs out of the original 20,000 burned out during the first 4 months?
After 2 months, 98% of the bulbs were still working.
After 8 months, 80% of the bulbs were still working.
We summarize all the data collected below: (Read carefully: the data was not collected at regular intervals.)
 How many bulbs out of the original 20,000 burned out during the first 4 months?
How many bulbs out of the original 20,000 burned out during the first 4 months?
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
78
On each of two days (January 1, 2005 and January 1, 2006), a person deposits $500 in a savings bank.The bank deposits interest in the account at a rate of 8%, compounded continuously.Choose the sum/integral that gives the size of the bank account at the end of 2006.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
79
A study of the costs to produce airplanes in World War II led to the theory of "learning curves," the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the xth plane is given by ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db5_88c1_ef84c72ee60a_TB4204_11.jpg) , where
, where ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db6_88c1_d799ebbba366_TB4204_11.jpg) = marginal cost to produce the first plane.[Note: You may use the fact that
= marginal cost to produce the first plane.[Note: You may use the fact that ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db7_88c1_d9450f2f9c37_TB4204_11.jpg) .] Recall that marginal cost is related to total cost as follows:
.] Recall that marginal cost is related to total cost as follows: ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db8_88c1_cf79d064b241_TB4204_11.jpg) , where C(x)= total cost to produce x units.
, where C(x)= total cost to produce x units.
Given this, and the formula for MC(x)with![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db9_88c1_77c7bef033fb_TB4204_11.jpg) = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?
= $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?
![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db5_88c1_ef84c72ee60a_TB4204_11.jpg) , where
, where ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db6_88c1_d799ebbba366_TB4204_11.jpg) = marginal cost to produce the first plane.[Note: You may use the fact that
= marginal cost to produce the first plane.[Note: You may use the fact that ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db7_88c1_d9450f2f9c37_TB4204_11.jpg) .] Recall that marginal cost is related to total cost as follows:
.] Recall that marginal cost is related to total cost as follows: ![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db8_88c1_cf79d064b241_TB4204_11.jpg) , where C(x)= total cost to produce x units.
, where C(x)= total cost to produce x units.Given this, and the formula for MC(x)with
![A study of the costs to produce airplanes in World War II led to the theory of learning curves, the idea of which is that the marginal cost per plane decreases over the duration of a production run.In other words, with experience, staff on an assembly line can produce planes with greater efficiency.The 90% learning curve describes a typical situation where the marginal cost, MC, to produce the x<sup>th</sup> plane is given by , where = marginal cost to produce the first plane.[Note: You may use the fact that .] Recall that marginal cost is related to total cost as follows: , where C(x)= total cost to produce x units. Given this, and the formula for MC(x)with = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?](https://storage.examlex.com/TB4204/11eb1831_d91a_5db9_88c1_77c7bef033fb_TB4204_11.jpg) = $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?
= $500,000, find a formula for C(x).If the constant for C(x)is $20 million, what is C(50), the cost of producing 50 planes, to the nearest thousand dollars?
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
80
You have a bank account that earns 8% nominal annual interest compounded continuously, and you want to have $90,000 in the bank account in five years so that you can buy a brand new Porsche.You decide to deposit money in the account at a constant continuous rate of K dollars per year.Use a Riemann sum followed by an integral to determine the value of K (to the nearest dollar)so that you will have the $90,000 after five years.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck


