Deck 3: Short-Cuts to Differentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/175
Play
Full screen (f)
Deck 3: Short-Cuts to Differentiation
1
Given 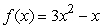 and
and 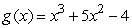 , find
, find 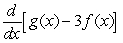 .
.
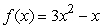 and
and 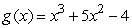 , find
, find 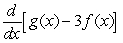 .
.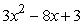
2
Consider the function 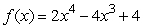 .Is f increasing or decreasing at the point x = 0.5?
.Is f increasing or decreasing at the point x = 0.5?
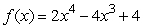 .Is f increasing or decreasing at the point x = 0.5?
.Is f increasing or decreasing at the point x = 0.5?decreasing
3
Find a formula for the slope of the tangent line to 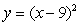
A)2x -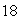
B)2x - 9
C)2(x - 9)3
D)(x - 9)3/3
E)none of the above
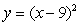
A)2x -
B)2x - 9
C)2(x - 9)3
D)(x - 9)3/3
E)none of the above
2x - 
4
Find the derivative of 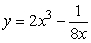 .
.
A)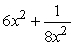
B)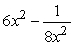
C)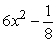
D)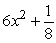
E)None of the above
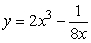 .
.A)
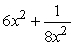
B)
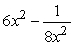
C)
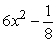
D)
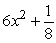
E)None of the above

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the function 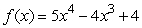 .Is f concave up or down at the point x = -0.2?
.Is f concave up or down at the point x = -0.2?
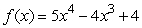 .Is f concave up or down at the point x = -0.2?
.Is f concave up or down at the point x = -0.2?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
6
If 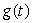 represents the position of a particle at time t seconds, then g'(t)represents the __________ of the particle at time t seconds.
represents the position of a particle at time t seconds, then g'(t)represents the __________ of the particle at time t seconds.
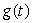 represents the position of a particle at time t seconds, then g'(t)represents the __________ of the particle at time t seconds.
represents the position of a particle at time t seconds, then g'(t)represents the __________ of the particle at time t seconds.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
7
Find the derivative of 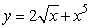 .
.
A)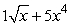
B)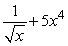
C)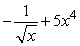
D)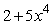
E)None of the above
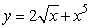 .
.A)
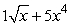
B)
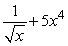
C)
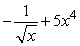
D)
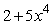
E)None of the above

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
8
The 12th derivative of 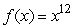 is 0.
is 0.
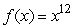 is 0.
is 0.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
9
If 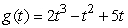 , then what is
, then what is 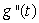 ?
?
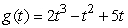 , then what is
, then what is 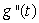 ?
?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
10
Given the variable  , find
, find  when
when  .
.
A)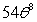
B)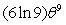
C)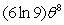
D)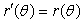
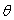 , find
, find 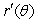 when
when 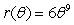 .
.A)
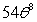
B)
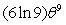
C)
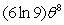
D)
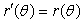

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
11
A man plans to propose to a woman in romantic fashion by taking her up in an air balloon.Unfortunately, he pulls the diamond ring from his pocket and drops it over the side of the balloon's basket.The ring's position above the earth t seconds after it falls is given by the function 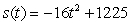 feet.How fast is the ring falling 3 seconds after he drops it?
feet.How fast is the ring falling 3 seconds after he drops it?
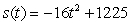 feet.How fast is the ring falling 3 seconds after he drops it?
feet.How fast is the ring falling 3 seconds after he drops it?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
12
A man plans to propose to a woman in romantic fashion by taking her up in an air balloon.Unfortunately, he pulls the diamond ring from his pocket and drops it over the side of the balloon's basket.The ring's position above the earth t seconds after it falls is given by the function 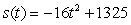 feet.How fast is the ring falling at the instant it hits the ground? 1325
feet.How fast is the ring falling at the instant it hits the ground? 1325
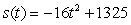 feet.How fast is the ring falling at the instant it hits the ground? 1325
feet.How fast is the ring falling at the instant it hits the ground? 1325
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the function 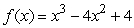 .Estimate
.Estimate 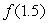 using the tangent line at x = 1.
using the tangent line at x = 1.
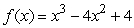 .Estimate
.Estimate 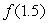 using the tangent line at x = 1.
using the tangent line at x = 1.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
14
Given 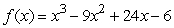 , at which value(s)of x does the curve have a horizontal tangent?
, at which value(s)of x does the curve have a horizontal tangent?
A)1
B)2
C)3
D)4
E)5
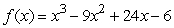 , at which value(s)of x does the curve have a horizontal tangent?
, at which value(s)of x does the curve have a horizontal tangent?A)1
B)2
C)3
D)4
E)5

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
15
Find the derivative of 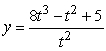 .
.
A)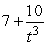
B)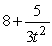
C)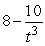
D)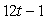
E)None of the above
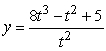 .
.A)
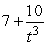
B)
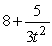
C)
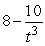
D)
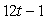
E)None of the above

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
16
Find 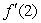 when
when 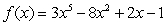 .
.
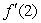 when
when 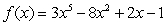 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
17
Find 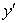 when
when 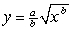 .
.
A)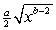
B)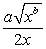
C)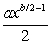
D)all of the above
E)none of the above
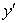 when
when 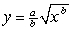 .
.A)
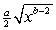
B)
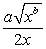
C)
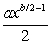
D)all of the above
E)none of the above

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
18
Given 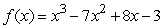 , what is the slope of the tangent line to the curve at x = -3?
, what is the slope of the tangent line to the curve at x = -3?
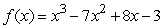 , what is the slope of the tangent line to the curve at x = -3?
, what is the slope of the tangent line to the curve at x = -3?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
19
Find the derivative of 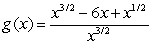 with respect to x.
with respect to x.
A)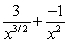
B)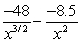
C)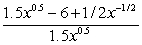
D)6x - 3
 with respect to x.
with respect to x.A)
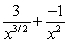
B)
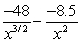
C)
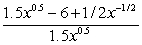
D)6x - 3

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
20
Differentiate 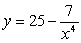 .
.
A)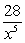
B)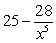
C)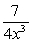
D)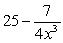
E)None of the above
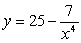 .
.A)
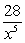
B)
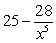
C)
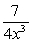
D)
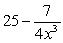
E)None of the above

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
21
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
22
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
23
A child earns five cents from her grandfather for each dandelion she pulls out of his front yard.The child pulls out all the dandelions that are there.As the season passes, the number of dandelions in the front yard increase according to the model 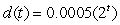 .After 15 days, her grandfather calls off the deal.How many dandelions does she pull on the 15th day? How fast is the number of dandelions increasing on the 15th day?
.After 15 days, her grandfather calls off the deal.How many dandelions does she pull on the 15th day? How fast is the number of dandelions increasing on the 15th day?
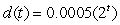 .After 15 days, her grandfather calls off the deal.How many dandelions does she pull on the 15th day? How fast is the number of dandelions increasing on the 15th day?
.After 15 days, her grandfather calls off the deal.How many dandelions does she pull on the 15th day? How fast is the number of dandelions increasing on the 15th day?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
24
Find the slope of the graph of 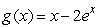 at the point where it crosses the y-axis.
at the point where it crosses the y-axis.
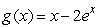 at the point where it crosses the y-axis.
at the point where it crosses the y-axis.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the following table of data for the function f.
Suppose g is a function such that g(5.1)= 9 and g'(5.1)= 3.Find h'(5.1)where h(x)= f(x)g(x).Use the right-hand estimate for .Round to 2 decimal places.
Suppose g is a function such that g(5.1)= 9 and g'(5.1)= 3.Find h'(5.1)where h(x)= f(x)g(x).Use the right-hand estimate for .Round to 2 decimal places.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
26
Prove that the function 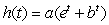 , where a > 1 and b > 1, is increasing for all values of t.
, where a > 1 and b > 1, is increasing for all values of t.
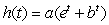 , where a > 1 and b > 1, is increasing for all values of t.
, where a > 1 and b > 1, is increasing for all values of t.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
27
With a yearly inflation rate of 7%, prices are described by 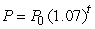 , where
, where 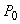 is the price in dollars when t = 0 and t is time in years.If
is the price in dollars when t = 0 and t is time in years.If 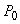 = 1.3, how fast (in cents/year)are prices rising when t = 19? Round to 1 decimal place.
= 1.3, how fast (in cents/year)are prices rising when t = 19? Round to 1 decimal place.
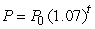 , where
, where 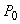 is the price in dollars when t = 0 and t is time in years.If
is the price in dollars when t = 0 and t is time in years.If 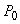 = 1.3, how fast (in cents/year)are prices rising when t = 19? Round to 1 decimal place.
= 1.3, how fast (in cents/year)are prices rising when t = 19? Round to 1 decimal place.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
28
On what intervals is the function 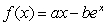 :
:
a)increasing?
b)decreasing?
c)concave up?
d)concave down?
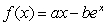 :
:a)increasing?
b)decreasing?
c)concave up?
d)concave down?

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the following table of data for the function f. What is the sign of f '(5.1)?
A)positive
B)negative
A)positive
B)negative

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
30
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
31
On what intervals is the polynomial 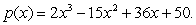 concave down? Concave up?
concave down? Concave up?
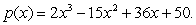 concave down? Concave up?
concave down? Concave up?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
32
Given 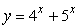 , find
, find 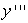 .
.
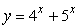 , find
, find 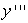 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the graph .What is the x-intercept of the tangent line to the graph at
A)
B)e a
C)
D)
A)
B)e a
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
34
If P dollars are invested at an annual rate of r%, then in t years this investment grows to F dollars, where .If you solve this equation for P and hold F and r constant, what will the sign of be?
A)positive
B)negative
A)positive
B)negative

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
35
Differentiate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
36
On what intervals is the polynomial 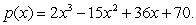 increasing? Decreasing?
increasing? Decreasing?
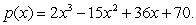 increasing? Decreasing?
increasing? Decreasing?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
37
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
38
If P dollars are invested at an annual rate of r%, then in t years this investment grows to F dollars, where .Assuming P and r are constant, find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
39
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
40
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
41
Given , , and h(x)= f(x)g(x), find h'(1).Round to 2 decimal places.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
42
Find the equation of the tangent line to 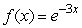 at x = 3 and use it find the point where the tangent line crosses the x-axis.Round to 2 decimal places.
at x = 3 and use it find the point where the tangent line crosses the x-axis.Round to 2 decimal places.
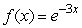 at x = 3 and use it find the point where the tangent line crosses the x-axis.Round to 2 decimal places.
at x = 3 and use it find the point where the tangent line crosses the x-axis.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
43
The table below gives values for functions f and g, and their derivatives.
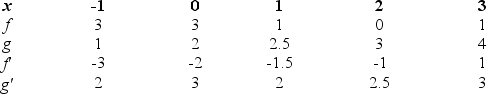 Find
Find 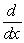 g(f(x))at x = -1.If is cannot be computed from the information given, enter "cannot find".
g(f(x))at x = -1.If is cannot be computed from the information given, enter "cannot find".
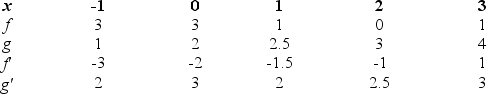 Find
Find 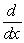 g(f(x))at x = -1.If is cannot be computed from the information given, enter "cannot find".
g(f(x))at x = -1.If is cannot be computed from the information given, enter "cannot find".
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
44
Use the product rule to write a proof of the constant multiple rule: 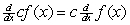 .
.
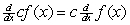 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
45
Let f(x)and g(x)be two functions.Values of f(x), f '(x), g(x), and g'(x)for x = 0, 1, and 2 are given in the table below.Use the information in the table to find if e g(x)
x.
A)
B)
C)
D)
x.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
46
Differentiate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
47
Find the second derivative of at x = 1.5.Round to three decimal places.
A)0.738
B)-0.105
C)0.316
D)-1.159
A)0.738
B)-0.105
C)0.316
D)-1.159

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
48
Determine the derivative rule for finding the derivative of the reciprocal function:
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
49
Given , , and h(x)= g(x)/f(x), find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
50
Given , , and h(x)= g(x)f(x), find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
51
A table of values for a function F near x = 3 and tables of values for a function G near x = 3 and near x = 7 are given below.If 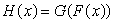 , estimate H'(3)using the chain rule.Use right-hand estimates for
, estimate H'(3)using the chain rule.Use right-hand estimates for 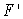 and
and 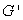 .
.


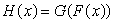 , estimate H'(3)using the chain rule.Use right-hand estimates for
, estimate H'(3)using the chain rule.Use right-hand estimates for 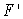 and
and 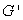 .
.


Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
52
The volume of a certain tree is given by 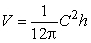 , where C is the circumference of the tree at the ground level and h is the height of the tree.If C is 4 feet and growing at the rate of 0.25 feet per year, and if h is 25 feet and is growing at 5 feet per year, find the rate of growth of the volume V (in ft3/yr).Round to 2 decimal places.
, where C is the circumference of the tree at the ground level and h is the height of the tree.If C is 4 feet and growing at the rate of 0.25 feet per year, and if h is 25 feet and is growing at 5 feet per year, find the rate of growth of the volume V (in ft3/yr).Round to 2 decimal places.
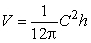 , where C is the circumference of the tree at the ground level and h is the height of the tree.If C is 4 feet and growing at the rate of 0.25 feet per year, and if h is 25 feet and is growing at 5 feet per year, find the rate of growth of the volume V (in ft3/yr).Round to 2 decimal places.
, where C is the circumference of the tree at the ground level and h is the height of the tree.If C is 4 feet and growing at the rate of 0.25 feet per year, and if h is 25 feet and is growing at 5 feet per year, find the rate of growth of the volume V (in ft3/yr).Round to 2 decimal places.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
53
A table of values for functions F and G near x = 3 is given below.If H(x)= F(x)/G(x), estimate H'(3)by using the quotient rule and then using right-hand estimates for 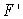 and
and 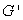 .Round to 2 decimal places.
.Round to 2 decimal places.

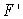 and
and 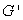 .Round to 2 decimal places.
.Round to 2 decimal places.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
54
Differentiate 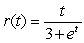 .
.
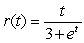 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
55
Find the slope of the line tangent to 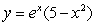 when x = 2.Round to two decimal places.
when x = 2.Round to two decimal places.
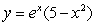 when x = 2.Round to two decimal places.
when x = 2.Round to two decimal places.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
56
The table below gives values for functions f and g, and their derivatives.
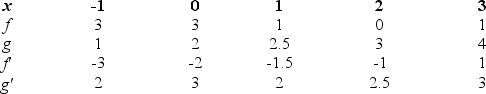 Find
Find 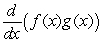 at x = 1.Round to 2 decimal places.
at x = 1.Round to 2 decimal places.
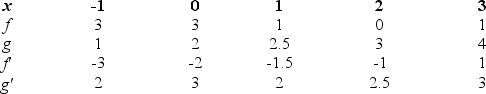 Find
Find 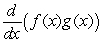 at x = 1.Round to 2 decimal places.
at x = 1.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
57
Let f(x)and g(x)be two functions.Values of f(x), f '(x), g(x), and g'(x)for x = 0, 1, and 2 are given in the table below.Use the information in the table to find if [f(x)]2.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
58
A table of values for a function F near x = 3 and tables of values for a function G near x = 3 and near x = 7 are given below.Estimate 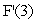 using the right-hand estimate.
using the right-hand estimate.


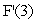 using the right-hand estimate.
using the right-hand estimate.


Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
59
What is the instantaneous rate of change of the function 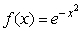 at x = 2? Round to 3 decimal places.
at x = 2? Round to 3 decimal places.
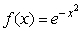 at x = 2? Round to 3 decimal places.
at x = 2? Round to 3 decimal places.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
60
Find the equation of the tangent line to 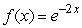 at x = 3 and use it to approximate the value of f(3.2).Round to 5 decimal places.
at x = 3 and use it to approximate the value of f(3.2).Round to 5 decimal places.
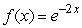 at x = 3 and use it to approximate the value of f(3.2).Round to 5 decimal places.
at x = 3 and use it to approximate the value of f(3.2).Round to 5 decimal places.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
61
A botanist in the field needs a quick estimate of the growth of jumping cholla cactus.In his study area, he has controlled the water and nutrients the jumping cholla receive so he can isolate the effect of sunlight on growth.He lets a function s(t)represent the average hours of sunlight per day in month t (where t = 1 is January).He lets a function g(s)represent the monthly growth of jumping cholla in centimeters at different sunlight exposures.From past experience, he quickly jots down the table below.
 Suppose
Suppose 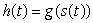 .
.
a)Find and interpret meaning of the quantity g(10).
b)Find and interpret the meaning of the quantity g'(10).
c)Find the interpret the meaning of the quantity h(10).
d)Find the interpret the meaning of the quantity h'(10).
 Suppose
Suppose 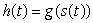 .
.a)Find and interpret meaning of the quantity g(10).
b)Find and interpret the meaning of the quantity g'(10).
c)Find the interpret the meaning of the quantity h(10).
d)Find the interpret the meaning of the quantity h'(10).

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
62
Find the derivative .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
63
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
64
Find the slope of the curve 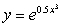 at x = 2 to the nearest whole number.
at x = 2 to the nearest whole number.
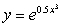 at x = 2 to the nearest whole number.
at x = 2 to the nearest whole number.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
65
Which is true of the following graph? 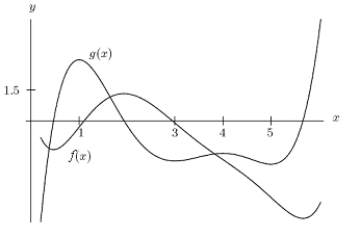
A)
B)

A)
B)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
66
Differentiate 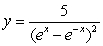 .
.
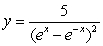 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
67
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
68
Find the derivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
69
Differentiate
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
70
If a and b are constants and 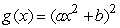 , find
, find 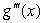 .
.
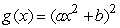 , find
, find 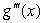 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
71
Find when .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
72
Find a function F(x)such that 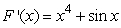 and F(0)= 5.
and F(0)= 5.
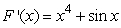 and F(0)= 5.
and F(0)= 5.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
73
Differentiate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
74
Differentiate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
75
Differentiate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
76
A particle moves in such a way that 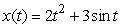 , where x is the horizontal distance the particle has traveled, in units, and t is time, in seconds.What is the average rate of change between t = 0 and
, where x is the horizontal distance the particle has traveled, in units, and t is time, in seconds.What is the average rate of change between t = 0 and 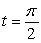 ? Specify units
? Specify units
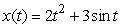 , where x is the horizontal distance the particle has traveled, in units, and t is time, in seconds.What is the average rate of change between t = 0 and
, where x is the horizontal distance the particle has traveled, in units, and t is time, in seconds.What is the average rate of change between t = 0 and 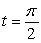 ? Specify units
? Specify units
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
77
Differentiate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
78
Find the critical number(s)of the curve 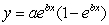 .
.
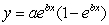 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
79
Find 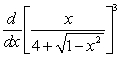 .
.
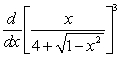 .
.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
80
A particle moves in such a way that 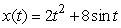 .What is the instantaneous rate of change at t = 0?
.What is the instantaneous rate of change at t = 0?
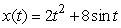 .What is the instantaneous rate of change at t = 0?
.What is the instantaneous rate of change at t = 0?
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck


