Deck 6: Constructing Antiderivatives
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/90
Play
Full screen (f)
Deck 6: Constructing Antiderivatives
1
Find a function F such that .
A)
B)
C)
D)
A)
B)
C)
D)
2
Given the values of the derivative f '(x)in the table and that f (0)= 60, estimate f (4).(Average left- and right-hand sums).
120
3
A young girl who aspires to be a rocket scientist launches a model rocket from the ground at time t = 0.The rocket travels straight up in the air, and the following graph shows the upward velocity of the rocket as a function of time: 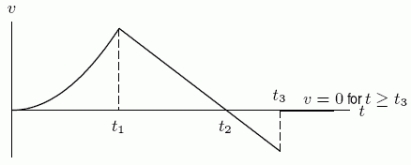 Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, which of the following is larger?
Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, which of the following is larger?
A)
B)
 Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, which of the following is larger?
Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, which of the following is larger?A)
B)
4
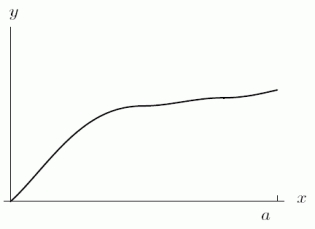
If is as shown in the first graph, could the function in the second graph represent the total area (i.e., not necessarily the definite integral)between f(x)and the x-axis from 0 to a? 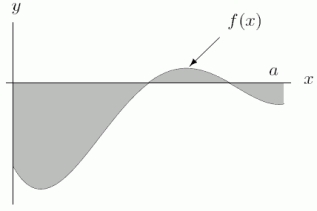



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
5
You decide to take a trip down a stretch of road that runs straight east and west.The following table gives your eastward velocity (in miles per minute)measured at one-minute intervals for the first ten minutes of your trip.
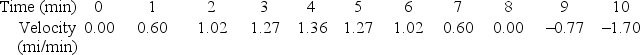 What is your best estimate of the total eastward distance of your car from your starting position after ten minutes? Round to the nearest whole number.
What is your best estimate of the total eastward distance of your car from your starting position after ten minutes? Round to the nearest whole number.
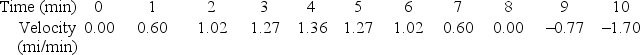 What is your best estimate of the total eastward distance of your car from your starting position after ten minutes? Round to the nearest whole number.
What is your best estimate of the total eastward distance of your car from your starting position after ten minutes? Round to the nearest whole number.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
6
Find a function F such that .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
7
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
8
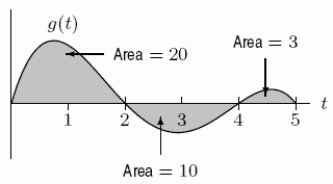
The graph of 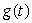 is shown in the following figure.If G is an antiderivative of g such that
is shown in the following figure.If G is an antiderivative of g such that 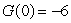 , what is
, what is 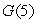 ?
? 
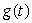 is shown in the following figure.If G is an antiderivative of g such that
is shown in the following figure.If G is an antiderivative of g such that 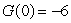 , what is
, what is 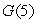 ?
? 

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
9
Estimate 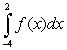 for the figure given.
for the figure given. 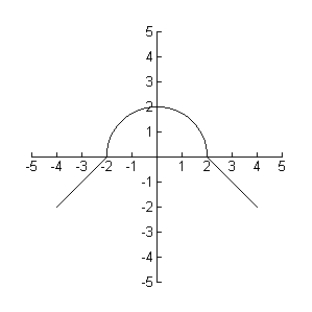
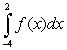 for the figure given.
for the figure given. 

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
10
Find the total area bounded between the curve 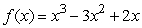 and the x-axis.Round to 3 decimal places.
and the x-axis.Round to 3 decimal places.
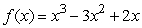 and the x-axis.Round to 3 decimal places.
and the x-axis.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
11
A young girl who aspires to be a rocket scientist launches a model rocket from the ground at time t = 0.The rocket travels straight up in the air, and the following graph shows the upward velocity of the rocket as a function of time: 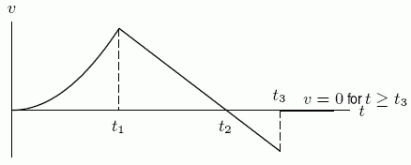 Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, what does the sign of mean physically?
Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, what does the sign of mean physically?
A)The rocket came to rest somewhere above the ground.
B)The rocket came to rest somewhere below the ground.
C)The rocket was accelerating when it hit the ground.
D)The rocket was decelerating when it hit the ground.
 Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, what does the sign of mean physically?
Let v(t)be the function that gives the velocity of the rocket at time t.From the graph of the rocket's velocity, what does the sign of mean physically?A)The rocket came to rest somewhere above the ground.
B)The rocket came to rest somewhere below the ground.
C)The rocket was accelerating when it hit the ground.
D)The rocket was decelerating when it hit the ground.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
12
Could the second function be an antiderivative of the first function? 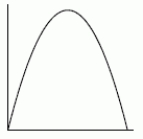
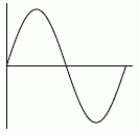



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
13
You decide to take a trip down a stretch of road that runs straight east and west.The following table gives your eastward velocity (in miles per minute)measured at one-minute intervals for the first ten minutes of your trip. Does the following graph give your acceleration or your eastward distance from your starting place as a function of time? 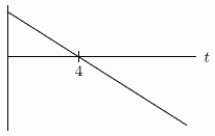
A)Your acceleration
B)Your eastward distance

A)Your acceleration
B)Your eastward distance

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
14
The rate of change in concentration of a certain medication in a person's body, H'(t), in micrograms per milliliter per minute, is -1 for the first 2 minutes.Then it increases at a constant rate for 2 minutes, reaching 1 at t = 4.Then it remains constant for 1 minute.Sketch H(t), assuming H(0)= 9.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
15
Sketch the graphs of 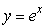 and y = ex.Find the average value of the difference between
and y = ex.Find the average value of the difference between 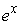 and ex on the interval between x = 0 and x = 1.5.Round to 2 decimal places.
and ex on the interval between x = 0 and x = 1.5.Round to 2 decimal places.
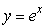 and y = ex.Find the average value of the difference between
and y = ex.Find the average value of the difference between 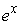 and ex on the interval between x = 0 and x = 1.5.Round to 2 decimal places.
and ex on the interval between x = 0 and x = 1.5.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
16
A young girl who aspires to be a rocket scientist launches a model rocket from the ground at time t = 0.The rocket travels straight up in the air, and the following graph shows the upward velocity of the rocket as a function of time: 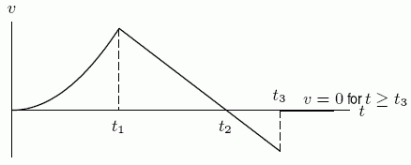 Let h be the height (or vertical displacement)of the rocket, let a be the acceleration of the rocket, and let h = 0 be the ground level from which the rocket was launched.Recall that the first derivative of displacement is velocity and that the first derivative of velocity is acceleration.Is the following a graph of the acceleration or the height of the rocket as a function of time?
Let h be the height (or vertical displacement)of the rocket, let a be the acceleration of the rocket, and let h = 0 be the ground level from which the rocket was launched.Recall that the first derivative of displacement is velocity and that the first derivative of velocity is acceleration.Is the following a graph of the acceleration or the height of the rocket as a function of time? 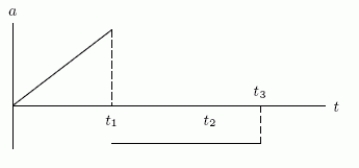
A)The acceleration.
B)The height.
 Let h be the height (or vertical displacement)of the rocket, let a be the acceleration of the rocket, and let h = 0 be the ground level from which the rocket was launched.Recall that the first derivative of displacement is velocity and that the first derivative of velocity is acceleration.Is the following a graph of the acceleration or the height of the rocket as a function of time?
Let h be the height (or vertical displacement)of the rocket, let a be the acceleration of the rocket, and let h = 0 be the ground level from which the rocket was launched.Recall that the first derivative of displacement is velocity and that the first derivative of velocity is acceleration.Is the following a graph of the acceleration or the height of the rocket as a function of time? 
A)The acceleration.
B)The height.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
17
Sketch the graphs of and y = ex.For which values of x is ? Mark all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
18
If f is shown in the first graph, which of the two functions F could have F' = f ? 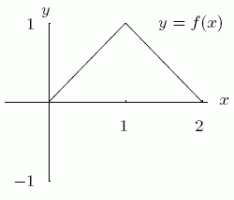
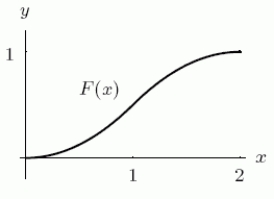
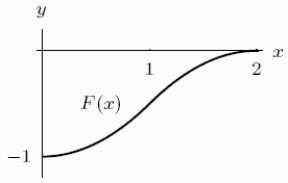
A)The first one
B)The second one
C)Both of them
D)Neither of them



A)The first one
B)The second one
C)Both of them
D)Neither of them

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
19
Sketch a graph of the antiderivative of g(x), given the graph g'(x)and g(0)=1. 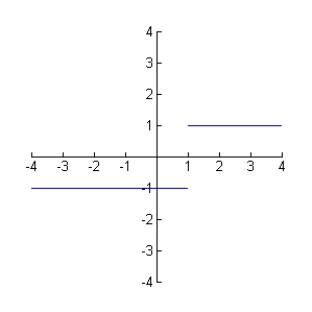


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
20
Is an antiderivative of ?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
21
On planet Janet the gravitational constant g is -10 feet per second per second: that is, for every second an object falls it picks up an extra 10 feet per second of velocity downward.A ball is thrown upward (from height zero)at time t = 0 at 40 feet per second.What is the peak height of the ball?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
22
A factory is dumping pollutants into a lake continuously at the rate of 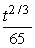 tons per week, where t is the time in weeks since the factory commenced operations.
tons per week, where t is the time in weeks since the factory commenced operations.
Assume that natural processes can remove up to 0.138 tons of pollutant per week from the lake and that there was no pollution in the lake when the factory commenced operations one year ago.How many tons of pollutant have now accumulated in the lake? (Note: The amount of pollutant being dumped into the lake is never negative.)Round to 2 decimal places.
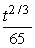 tons per week, where t is the time in weeks since the factory commenced operations.
tons per week, where t is the time in weeks since the factory commenced operations.Assume that natural processes can remove up to 0.138 tons of pollutant per week from the lake and that there was no pollution in the lake when the factory commenced operations one year ago.How many tons of pollutant have now accumulated in the lake? (Note: The amount of pollutant being dumped into the lake is never negative.)Round to 2 decimal places.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
23
Find the area above and below .
A)9.7980
B)29.3939
C)19.5959
D)-19.5959
E)2.2020
A)9.7980
B)29.3939
C)19.5959
D)-19.5959
E)2.2020

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
24
A car is going 64 feet per second and the driver puts on the brakes, bringing the car to a stop in 4 seconds.Assume the deceleration of the car is constant while the brakes are on.The acceleration (really deceleration)of the car is _____ ft/sec.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
25
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
26
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
27
A factory is dumping pollutants into a lake continuously at the rate of 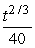 tons per week, where t is the time in weeks since the factory commenced operations.After one year of operation, how many tons of pollutant has the factory dumped into the lake? Round to 2 decimal places.
tons per week, where t is the time in weeks since the factory commenced operations.After one year of operation, how many tons of pollutant has the factory dumped into the lake? Round to 2 decimal places.
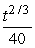 tons per week, where t is the time in weeks since the factory commenced operations.After one year of operation, how many tons of pollutant has the factory dumped into the lake? Round to 2 decimal places.
tons per week, where t is the time in weeks since the factory commenced operations.After one year of operation, how many tons of pollutant has the factory dumped into the lake? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
28
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
29
Determine: 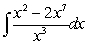
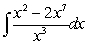

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose .Find the total area bounded by F(x), x = 0, x = and y = 0.Round to 2 decimal places.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
31
Find the general antiderivative of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
32
A ball is dropped from a window 80 feet above the ground.Assume that its acceleration is a(t)= -32 ft/sec2 for t 0.After how many seconds does it hit the ground? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose the rate at which ice in a skating pond is melting is given by 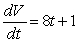 , where V is the volume of the ice in cubic feet, and t is the time in minutes.Use a definite integral to find how many cubic feet of ice have melted in the first 2 minutes.
, where V is the volume of the ice in cubic feet, and t is the time in minutes.Use a definite integral to find how many cubic feet of ice have melted in the first 2 minutes.
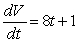 , where V is the volume of the ice in cubic feet, and t is the time in minutes.Use a definite integral to find how many cubic feet of ice have melted in the first 2 minutes.
, where V is the volume of the ice in cubic feet, and t is the time in minutes.Use a definite integral to find how many cubic feet of ice have melted in the first 2 minutes.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
34
A car is going 56 feet per second and the driver puts on the brakes, bringing the car to a stop in 4 seconds.Assume the deceleration of the car is constant while the brakes are on.How many feet does the car travel from the time the brakes are applied until it stops?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
35
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
36
A ball is dropped from a window 140 feet above the ground.Assume that its acceleration is a(t)= -32 ft/sec2 for t 0.Find the velocity of the ball as a function of time t.(All answers are in ft/sec.)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
37
On planet Janet the gravitational constant g is -11 feet per second per second: that is, for every second an object falls it picks up an extra 11 feet per second of velocity downward.A ball is thrown upward at time t = 0 at 44 feet per second.After how many seconds does the ball reach the peak of its flight?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
38
Find the exact area between the graphs of and for 0 x 5.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
39
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
40
A car is going 85 feet per second and the driver puts on the brakes, bringing the car to a stop in 5 seconds.Assume the deceleration of the car is constant while the brakes are on.Suppose a second car is traveling the same speed and the brakes are twice as strong (can stop the car twice as fast)as those in the first car.How far does the second car travel before it stops?
A)Half as far as the first car.
B)Twice as far as the first car.
C)The same distance as the first car.
D)Four times as far as the first car.
E)One-fourth as far as the first car.
A)Half as far as the first car.
B)Twice as far as the first car.
C)The same distance as the first car.
D)Four times as far as the first car.
E)One-fourth as far as the first car.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
41
Below are the graphs of (i) , and (ii) (not necessarily in that order). 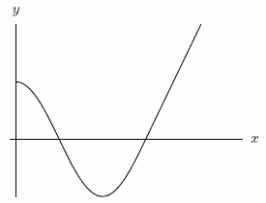
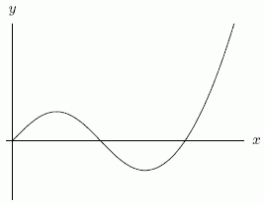 Which one is the graph of (ii)?
Which one is the graph of (ii)?
A)The first one.
B)The second one.

 Which one is the graph of (ii)?
Which one is the graph of (ii)?A)The first one.
B)The second one.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
42
The police observe that the skid marks made by a stopping car are 240 ft long.Assuming the car decelerated at a constant rate of 21 ft/ sec2, skidding all the way, how fast was the car going when the brakes were applied? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
43
Let 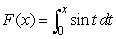 and
and 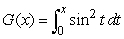 .If A, B, C, D, J, and K represent positive areas as shown in the graph, what combination of these areas represent G
.If A, B, C, D, J, and K represent positive areas as shown in the graph, what combination of these areas represent G 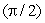 on the graph?
on the graph? 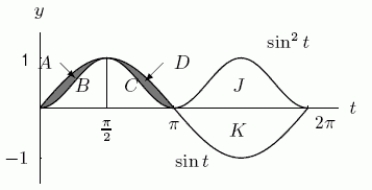
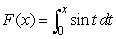 and
and 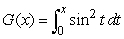 .If A, B, C, D, J, and K represent positive areas as shown in the graph, what combination of these areas represent G
.If A, B, C, D, J, and K represent positive areas as shown in the graph, what combination of these areas represent G 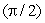 on the graph?
on the graph? 

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
44
A dog's bone is tossed in a yard traveling with a vertical velocity of 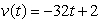 feet/sec.Determine the maximum height reached by the bone.
feet/sec.Determine the maximum height reached by the bone.
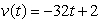 feet/sec.Determine the maximum height reached by the bone.
feet/sec.Determine the maximum height reached by the bone.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate .Some of the coefficients may not be reduced.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
46
Find the general solution of the differential equation 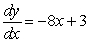 .
.
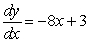 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
47
Assuming the 440 feet is accurate and you neglect air resistance, determine the accuracy of the following paragraph: MY JOURNEY BENEATH THE EARTH
Condensed from "A Wolverine is Eating My Leg"
Tim Cahill:
I am in Ellison's Cave, about to rappel down Incredible Pit, the second-deepest cave pit in the continental United States.The drop is 440 feet, about what you'd experience from the top of a 40-story building.If you took the shaft in a free fall, you'd accelerate to more than 100 miles an hour and then--about five seconds into the experience--you'd decelerate to zero.And die.
A)The time (about 5 seconds)is fairly accurate, but the speed (more than 100 mph)is not.
B)The speed (more than 100 mph)is fairly accurate, but the time (about 5 seconds)is not.
C)Both of the numbers are fairly accurate.
D)Neither of the numbers are fairly accurate
Condensed from "A Wolverine is Eating My Leg"
Tim Cahill:
I am in Ellison's Cave, about to rappel down Incredible Pit, the second-deepest cave pit in the continental United States.The drop is 440 feet, about what you'd experience from the top of a 40-story building.If you took the shaft in a free fall, you'd accelerate to more than 100 miles an hour and then--about five seconds into the experience--you'd decelerate to zero.And die.
A)The time (about 5 seconds)is fairly accurate, but the speed (more than 100 mph)is not.
B)The speed (more than 100 mph)is fairly accurate, but the time (about 5 seconds)is not.
C)Both of the numbers are fairly accurate.
D)Neither of the numbers are fairly accurate

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
49
On planet Janet the gravitational constant g is -10 feet per second per second: that is, for every second an object falls it picks up an extra 10 feet per second of velocity downward.A ball is thrown upward at time t = 0 at 25 feet per second.On planet Nanette, g is one-fourth as great as on Janet.What is the peak height of the ball on planet Nanette?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
50
A ball is thrown vertically upwards from the top of a 256-foot cliff with initial velocity of 96 feet per second.Find its maximum height (in ft).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
51
A function g is known to be linear on the interval from to 2 (inclusive)and also linear on the interval from 2 to (again inclusive).
Furthermore, g(1)= 2, g(2)= 0, g(4)= 8.Another function f satisfies f (0)= 0 and f ' = g.What is ?
Furthermore, g(1)= 2, g(2)= 0, g(4)= 8.Another function f satisfies f (0)= 0 and f ' = g.What is ?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
52
The function f(t)is graphed below and we define . 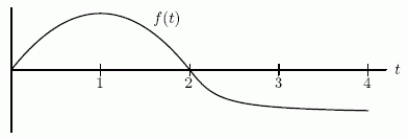 Is concave down for x =1/2?
Is concave down for x =1/2?
 Is concave down for x =1/2?
Is concave down for x =1/2? 
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
53
For 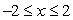 , define
, define 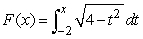 .What is the value of
.What is the value of 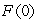 ? Round to 2 decimal places.
? Round to 2 decimal places.
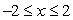 , define
, define 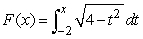 .What is the value of
.What is the value of 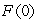 ? Round to 2 decimal places.
? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
54
For -1 x 1, define .What does F(1)represent geometrically?
A)The area of a quarter circle of radius 1.
B)The area of a circle of radius 1.
C)The area of a semicircle of radius 1.
D)None of the above
A)The area of a quarter circle of radius 1.
B)The area of a circle of radius 1.
C)The area of a semicircle of radius 1.
D)None of the above

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
55
Find the solution of the differential equation 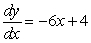 satisfying
satisfying 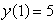 .
.
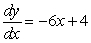 satisfying
satisfying 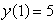 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
56
Below are the graphs of (i) , (ii) , and (iii) (not necessarily in that order). 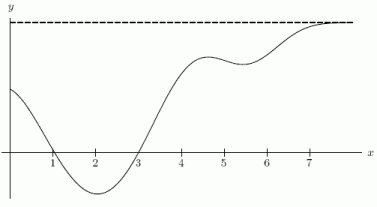
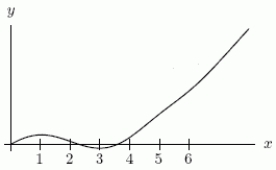
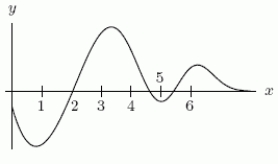 Which one is the graph of (iii)?
Which one is the graph of (iii)?
A)The first one.
B)The third one.
C)The second one.


 Which one is the graph of (iii)?
Which one is the graph of (iii)?A)The first one.
B)The third one.
C)The second one.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate 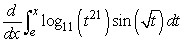 .
.
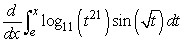 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
59
For , define .Find F'(x).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
60
Find the solution of the initial value problems when .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
61
For 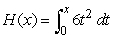 , find
, find 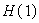 .
.
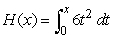 , find
, find 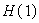 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate 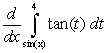 .
.
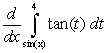 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
63
Find an antiderivative F(x)with F'(x)= f (x)and F(0)= 3 when .

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
64
The area between 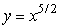 , the x-axis, and x = b is approximately 79.9.Find the value of b using the Fundamental Theorem.Round to 1 decimal place.
, the x-axis, and x = b is approximately 79.9.Find the value of b using the Fundamental Theorem.Round to 1 decimal place.
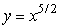 , the x-axis, and x = b is approximately 79.9.Find the value of b using the Fundamental Theorem.Round to 1 decimal place.
, the x-axis, and x = b is approximately 79.9.Find the value of b using the Fundamental Theorem.Round to 1 decimal place.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
65
A boat has constant deceleration.It was initially moving at 80 mph and stopped in a distance of 300 feet.The rate of deceleration is _____ ft/ sec2.(Note: 1 mph = 22/15 ft/ sec.)Round to 2 decimal places.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
66
A boulder is dropped from a cliff.A second boulder is dropped from a cliff that is half as high.How does the speed of the second boulder upon impact compare with that of the first?
A)Ths speed of the second is approximately 0.5 times the speed of the first.
B)Ths speed of the second is approximately 0.7 times the speed of the first.
C)Ths speed of the second is approximately 0.25 times the speed of the first.
D)Ths speed of the second is approximately 2 times the speed of the first.
E)Ths speed of the second is approximately the same as the speed of the first.
A)Ths speed of the second is approximately 0.5 times the speed of the first.
B)Ths speed of the second is approximately 0.7 times the speed of the first.
C)Ths speed of the second is approximately 0.25 times the speed of the first.
D)Ths speed of the second is approximately 2 times the speed of the first.
E)Ths speed of the second is approximately the same as the speed of the first.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
67
Use the Fundamental Theorem of Calculus to evaluate 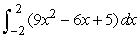 .
.
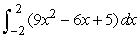 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate 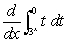 .
.
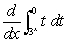 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
69
At time t = 0, a bowling ball rolls off a 250-meter ledge with velocity 30 meters/sec downward.Express its height, h(t), in meters above the ground as a function of time, t, in seconds.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
70
Find the area of the region between 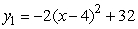 and
and 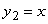 , accurate to 2 decimal places.
, accurate to 2 decimal places.
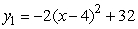 and
and 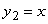 , accurate to 2 decimal places.
, accurate to 2 decimal places.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
71
On the moon the acceleration due to gravity is 5 feet/ sec2.A brick is dropped from the top of a tower on the moon and hits the ground in 16 seconds.How many feet high is the tower?

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
72
The general solution of the differential equation is .

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
73
A boulder is dropped from a 150-foot cliff.How fast is it going when it hits the ground? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
74
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
75
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
76
Write an expression for the function, f(x), with and .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
77
Suppose the acceleration due to gravity on Planet A is twice that of Planet B.A brick dropped from the top of a tower on Planet A takes 20 seconds to hit the ground.A brick dropped from the top of a tower on Planet B also takes 20 seconds to hit the ground.How does the height of the tower on Planet A compare with the height of the tower on Planet B?
A)The tower on Planet A is 4 times the height of the one on Planet B.
B)The tower on Planet A is twice the height of the one on Planet B.
C)The tower on Planet A is half the height of the one on Planet B.
D)The tower on Planet A is the same as the height of the one on Planet B.
A)The tower on Planet A is 4 times the height of the one on Planet B.
B)The tower on Planet A is twice the height of the one on Planet B.
C)The tower on Planet A is half the height of the one on Planet B.
D)The tower on Planet A is the same as the height of the one on Planet B.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate 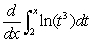 .
.
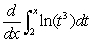 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate 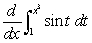 .
.
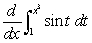 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
80
Find the value of G( /2)where G '(x)= 2 sin x cos x and G(0)= 1.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck


