Deck 4: Basic Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/171
Play
Full screen (f)
Deck 4: Basic Probability
1
Simple probability is also called
A)marginal probability.
B)joint probability.
C)conditional probability.
D)Bayes' theorem.
A)marginal probability.
B)joint probability.
C)conditional probability.
D)Bayes' theorem.
marginal probability.
2
If two events are mutually exclusive, what is the probability that both occur at the same time?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
0.
3
If event A and event B cannot occur at the same time, then events A and B are said to be
A)mutually exclusive.
B)independent.
C)collectively exhaustive.
D)None of the above.
A)mutually exclusive.
B)independent.
C)collectively exhaustive.
D)None of the above.
mutually exclusive.
4
If two events are collectively exhaustive, what is the probability that one or the other occurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
5
When using the general multiplication rule, P (A and B) is equal to
A)P(A|B)P(B).
B)P(A)P(B).
C)P(B)/P(A).
D)P(A)/P(B).
A)P(A|B)P(B).
B)P(A)P(B).
C)P(B)/P(A).
D)P(A)/P(B).

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
6
Selection of raffle tickets from a large bowl is an example of
A)simple probability.
B)sampling without replacement.
C)subjective probability.
D)None of the above.
A)simple probability.
B)sampling without replacement.
C)subjective probability.
D)None of the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
7
If the outcome of event A is not affected by event B, then events A and B are said to be
A)mutually exclusive.
B)independent.
C)collectively exhaustive.
D)None of the above.
A)mutually exclusive.
B)independent.
C)collectively exhaustive.
D)None of the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
8
If two events are mutually exclusive and collectively exhaustive, what is the probability that one or the other occurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
9
All the events in the sample space that are not part of the specified event are called
A)simple events.
B)joint events.
C)the sample space.
D)the complement of the event.
A)simple events.
B)joint events.
C)the sample space.
D)the complement of the event.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
10
A business venture can result in the following outcomes (with their corresponding chance of occurring in parentheses): Highly Successful (10%), Successful (25%), Break Even (25%), Disappointing (20%), and Highly Disappointing (?).If these are the only outcomes possible for the business venture, what is the chance that the business venture will be considered Highly Disappointing?
A)10%
B)15%
C)20%
D)25%
A)10%
B)15%
C)20%
D)25%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
11
If two events are mutually exclusive, what is the probability that one or the other occurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
12
If two equally likely events A and B are mutually exclusive, what is the probability that event Aoccurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
13
If events A and B are mutually exclusive and collectively exhaustive, what is the probability that event A occurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
14
If two equally likely events A and B are mutually exclusive and collectively exhaustive, what is the probability that event A occurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
15
If two events are independent, what is the probability that they both occur?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
16
If two events are mutually exclusive and collectively exhaustive, what is the probability that both occur?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
17
The collection of all possible events is called
A)a simple probability.
B)a sample space.
C)a joint probability.
D)the null set.
A)a simple probability.
B)a sample space.
C)a joint probability.
D)the null set.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
18
If two equally likely events A and B are collectively exhaustive, what is the probability that eventA occurs?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
19
If two events are collectively exhaustive, what is the probability that both occur at the same time?
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.
A)0.
B)0.50.
C)1.00.
D)Cannot be determined from the information given.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
20
If either event A or event B must occur, then events A and B are said to be
A)mutually exclusive.
B)independent.
C)collectively exhaustive.
D)None of the above.
A)mutually exclusive.
B)independent.
C)collectively exhaustive.
D)None of the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
21
The probability that house sales will increase in the next 6 months is estimated to be 0.25.The probability that the interest rates on housing loans will go up in the same period is estimated to be0.74.The probability that house sales or interest rates will go up during the next 6 months is estimated to be 0.89.The events increase in house sales and no increase in house sales in the next6 months are
A)independent.
B)mutually exclusive.
C)collectively exhaustive.
D)(b)and (c)
A)independent.
B)mutually exclusive.
C)collectively exhaustive.
D)(b)and (c)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
22
The employees of a company were surveyed on questions regarding their educational background(college degree or no college degree) and marital status (single or married).Of the 600 employees, 400 had college degrees, 100 were single, and 60 were single college graduates.The probability that an employee of the company is married and has a college degree is:
A)0.0667
B)0.567
C)0.667
D)0.833
A)0.0667
B)0.567
C)0.667
D)0.833

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
23
The probability that house sales will increase in the next 6 months is estimated to be 0.25.The probability that the interest rates on housing loans will go up in the same period is estimated to be0.74.The probability that house sales or interest rates will go up during the next 6 months is estimated to be 0.89.The probability that neither house sales nor interest rates will increase during the next 6 months is:
A)0.10
B)0.195
C)0.89
D)0.90
A)0.10
B)0.195
C)0.89
D)0.90

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
24
According to a survey of American households, the probability that the residents own 2 cars if annual household income is over $50,000 is 80%.Of the households surveyed, 60% had incomes over $50,000 and 70% had 2 cars.The probability that the residents of a household do not own 2 cars and have an income over $50,000 a year is:
A)0.12
B)0.18
C)0.22
D)0.48
A)0.12
B)0.18
C)0.22
D)0.48

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
25
A survey of banks revealed the following distribution for the interest rate being charged on a home loan (based on a 30-year mortgage with a 10% down payment) on a certain date in the past. If a bank is selected at random from this distribution, what is the chance that the interest rate charged on a home loan will exceed 3.49%?
A)0.06
B)0.41
C)0.59
D)1.00
A)0.06
B)0.41
C)0.59
D)1.00

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
26
A company has 2 machines that produce widgets.An older machine produces 23% defective widgets, while the new machine produces only 8% defective widgets.In addition, the new machine produces 3 times as many widgets as the older machine does.What is the probability that a randomly chosen widget produced by the company is defective?
A)0.078
B)0.1175
C)0.156
D)0.310
A)0.078
B)0.1175
C)0.156
D)0.310

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
27
The probability that house sales will increase in the next 6 months is estimated to be 0.25.The probability that the interest rates on housing loans will go up in the same period is estimated to be0.74.The probability that house sales or interest rates will go up during the next 6 months is estimated to be 0.89.The probability that both house sales and interest rates will increase during the next 6 months is:
A)0.10
B)0.185
C)0.705
D)0.90
A)0.10
B)0.185
C)0.705
D)0.90

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
28
The probability that house sales will increase in the next 6 months is estimated to be 0.25.The probability that the interest rates on housing loans will go up in the same period is estimated to be0.74.The probability that house sales or interest rates will go up during the next 6 months is estimated to be 0.89.The probability that house sales will increase but interest rates will not during the next 6 months is:
A)0.065
B)0.15
C)0.51
D)0.89
A)0.065
B)0.15
C)0.51
D)0.89

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
29
A company has 2 machines that produce widgets.An older machine produces 23% defective widgets, while the new machine produces only 8% defective widgets.In addition, the new machine produces 3 times as many widgets as the older machine does.Given that a widget was produced by the new machine, what is the probability it is not defective?
A)0.06
B)0.50
C)0.92
D)0.94
A)0.06
B)0.50
C)0.92
D)0.94

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
30
According to a survey of American households, the probability that the residents own 2 cars if annual household income is over $50,000 is 80%.Of the households surveyed, 60% had incomes over $50,000 and 70% had 2 cars.The probability that the residents do not own 2 cars if annual household income is not over $50,000 is:
A)0.12
B)0.18
C)0.45
D)0.70
A)0.12
B)0.18
C)0.45
D)0.70

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
31
According to a survey of American households, the probability that the residents own 2 cars if annual household income is over $50,000 is 80%.Of the households surveyed, 60% had incomes over $50,000 and 70% had 2 cars.The probability that the residents of a household own 2 cars and have an income over $50,000 a year is:
A)0.12
B)0.18
C)0.22
D)0.48
A)0.12
B)0.18
C)0.22
D)0.48

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
32
The probability that a new advertising campaign will increase sales is assessed as being 0.80.The probability that the cost of developing the new ad campaign can be kept within the originalbudget allocation is 0.40.If the two events are independent, the probability that neither the cost is kept within budget nor the campaign will increase sales is:
A)0.12
B)0.32
C)0.68
D)0.88
A)0.12
B)0.32
C)0.68
D)0.88

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
33
According to a survey of American households, the probability that the residents own 2 cars if annual household income is over $50,000 is 80%.Of the households surveyed, 60% had incomes over $50,000 and 70% had 2 cars.The probability that annual household income is over $50,000 if the residents of a household own 2 cars is:
A)0.42
B)0.48
C)0.50
D)0.69
A)0.42
B)0.48
C)0.50
D)0.69

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
34
The employees of a company were surveyed on questions regarding their educational background(college degree or no college degree) and marital status (single or married).Of the 600 employees, 400 had college degrees, 100 were single, and 60 were single college graduates.The probability that an employee of the company is single or has a college degree is:
A)0.10
B)0.25
C)0.667
D)0.733
A)0.10
B)0.25
C)0.667
D)0.733

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
35
The probability that a new advertising campaign will increase sales is assessed as being 0.80.The probability that the cost of developing the new ad campaign can be kept within the originalbudget allocation is 0.40.If the two events are independent, the probability that the cost is not kept within budget or the campaign will not increase sales is:
A)0.12
B)0.32
C)0.68
D)0.88
A)0.12
B)0.32
C)0.68
D)0.88

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
36
The probability that a new advertising campaign will increase sales is assessed as being 0.80.The probability that the cost of developing the new ad campaign can be kept within the originalbudget allocation is 0.40.If the two events are independent, the probability that the cost is kept within budget or the campaign will increase sales is:
A)0.20
B)0.32
C)0.68
D)0.88
A)0.20
B)0.32
C)0.68
D)0.88

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
37
According to a survey of American households, the probability that the residents own 2 cars if annual household income is over $50,000 is 80%.Of the households surveyed, 60% had incomes over $50,000 and 70% had 2 cars.The probability that annual household income is over $50,000 if the residents of a household do not own 2 cars is:
A)0.12
B)0.18
C)0.40
D)0.70
A)0.12
B)0.18
C)0.40
D)0.70

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
38
The probability that a new advertising campaign will increase sales is assessed as being 0.80.The probability that the cost of developing the new ad campaign can be kept within the originalbudget allocation is 0.40.If the two events are independent, the probability that the cost is kept within budget and the campaign will increase sales is:
A)0.20
B)0.32
C)0.40
D)0.88
A)0.20
B)0.32
C)0.40
D)0.88

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
39
The employees of a company were surveyed on questions regarding their educational background(college degree or no college degree) and marital status (single or married).Of the 600 employees, 400 had college degrees, 100 were single, and 60 were single college graduates.The probability that an employee of the company does not have a college degree is:
A)0.10
B)0.33
C)0.67
D)0.75
A)0.10
B)0.33
C)0.67
D)0.75

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
40
The probability that house sales will increase in the next 6 months is estimated to be 0.25.The probability that the interest rates on housing loans will go up in the same period is estimated to be0.74.The probability that house sales or interest rates will go up during the next 6 months is estimated to be 0.89.The events increase in house sales and increase in interest rates in the next 6 months are
A)independent.
B)mutually exclusive.
C)collectively exhaustive.
D)None of the above.
A)independent.
B)mutually exclusive.
C)collectively exhaustive.
D)None of the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
41
The collection of all the possible events is called a sample space.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
42
When A and B are mutually exclusive, P (A or B) can be found by adding P(A) andP(B).

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
43
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given alcohol was involved, what proportion of accidents involved a single vehicle?
A) 50 / 75 or 66.67%
B) 50 / 170 or 29.41%.
C) 120 / 170 or 70.59%
D) 120 / 400 or 30%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given alcohol was involved, what proportion of accidents involved a single vehicle?
A) 50 / 75 or 66.67%
B) 50 / 170 or 29.41%.
C) 120 / 170 or 70.59%
D) 120 / 400 or 30%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
44
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that multiple vehicles were involved, what proportion of accidents involved alcohol?
A) 120 / 170 or 70.59%
B) 120 / 230 or 52.17%
C) 120 / 325 or 36.92%
D) 120 / 400 or 30%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that multiple vehicles were involved, what proportion of accidents involved alcohol?
A) 120 / 170 or 70.59%
B) 120 / 230 or 52.17%
C) 120 / 325 or 36.92%
D) 120 / 400 or 30%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
45
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, what proportion of accidents involved alcohol or a single vehicle?
A) 25 / 400 or 6.25%
B) 50 / 400 or 12.5%
C) 195 / 400 or 48.75%
D) 245 / 400 or 61.25%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, what proportion of accidents involved alcohol or a single vehicle?
A) 25 / 400 or 6.25%
B) 50 / 400 or 12.5%
C) 195 / 400 or 48.75%
D) 245 / 400 or 61.25%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
46
SCENARIO 4-2
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, the events "Did Well on Midterm" and "Studying for Exam" are
A)not dependent.
B)not mutually exclusive.
C)collective exhaustive.
D)None of the above.
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, the events "Did Well on Midterm" and "Studying for Exam" are
A)not dependent.
B)not mutually exclusive.
C)collective exhaustive.
D)None of the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
47
SCENARIO 4-2
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, what is the probability that a randomly selected student did well on the midterm or went bar hopping the weekend before the midterm?
A) 30 / 200 or 15%
B) (80+30) / 200 or (30+80) / 200 or 55%
C) (30+70) / 200 or (70+30) / 200 or 50%
D) (80+30+70) / 200 or (110+100-30) / 200 or 90%
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, what is the probability that a randomly selected student did well on the midterm or went bar hopping the weekend before the midterm?
A) 30 / 200 or 15%
B) (80+30) / 200 or (30+80) / 200 or 55%
C) (30+70) / 200 or (70+30) / 200 or 50%
D) (80+30+70) / 200 or (110+100-30) / 200 or 90%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
48
If either A or B must occur they are called mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
49
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that alcohol was not involved, what proportion of the accidents were single vehicle?
A) 50 / 75 or 66.67%
B) 25 / 230 or 10.87%
C) 50 / 170 or 29.41%
D) 25 / 75 or 33.33%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that alcohol was not involved, what proportion of the accidents were single vehicle?
A) 50 / 75 or 66.67%
B) 25 / 230 or 10.87%
C) 50 / 170 or 29.41%
D) 25 / 75 or 33.33%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
50
SCENARIO 4-2
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, what is the probability that a randomly selected student who went bar hopping did well on the midterm?
A) 30 / 100 or 30%
B) 30 / 110 or 27.27%
C) 30 / 200 or 15%
D) (100 / 200)^{*}(110 / 200) or 27.50%
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, what is the probability that a randomly selected student who went bar hopping did well on the midterm?
A) 30 / 100 or 30%
B) 30 / 110 or 27.27%
C) 30 / 200 or 15%
D) (100 / 200)^{*}(110 / 200) or 27.50%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
51
SCENARIO 4-2
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, the events "Did Well on Midterm" and "Studying for Exam" are
A)dependent.
B)mutually exclusive.
C)collective exhaustive.
D)None of the above.
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, the events "Did Well on Midterm" and "Studying for Exam" are
A)dependent.
B)mutually exclusive.
C)collective exhaustive.
D)None of the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
52
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, what proportion of accidents involved more than one vehicle?
A)50/400 or 12.5%
B)75/400 or 18.75%
C)275/400 or 68.75%
D)325/400 or 81.25%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, what proportion of accidents involved more than one vehicle?
A)50/400 or 12.5%
B)75/400 or 18.75%
C)275/400 or 68.75%
D)325/400 or 81.25%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
53
A company has 2 machines that produce widgets.An older machine produces 23% defective widgets, while the new machine produces only 8% defective widgets.In addition, the new machine produces 3 times as many widgets as the older machine does.Given a randomly chosen widget was tested and found to be defective, what is the probability it was produced by the new machine?
A)0.08
B)0.15
C)0.489
D)0.511
A)0.08
B)0.15
C)0.489
D)0.511

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
54
If A and B cannot occur at the same time they are called mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
55
If either A or B must occur they are called collectively exhaustive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
56
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, what proportion of accidents involved alcohol and a single vehicle?
A) 25 / 400 or 6.25%
B) 50 / 400 or 12.5%
C) 195 / 400 or 48.75%
D) 245 / 400 or 61.25%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, what proportion of accidents involved alcohol and a single vehicle?
A) 25 / 400 or 6.25%
B) 50 / 400 or 12.5%
C) 195 / 400 or 48.75%
D) 245 / 400 or 61.25%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
57
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that alcohol was not involved, what proportion of the accidents were multiple vehicle?
A) 50 / 170 or 29.41%
B) 120 / 170 or 70.59%
C) 205 / 230 or 89.13%
D) 25 / 230 or 10.87%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that alcohol was not involved, what proportion of the accidents were multiple vehicle?
A) 50 / 170 or 29.41%
B) 120 / 170 or 70.59%
C) 205 / 230 or 89.13%
D) 25 / 230 or 10.87%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
58
SCENARIO 4-1
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that 3 vehicles were involved, what proportion of accidents involved alcohol?
A) 20 / 30 or 66.67%
B) 20 / 50 or 40%
C) 20 / 170 or 11.77%
D) 20 / 400 or 5%
Mothers Against Drunk Driving is a very visible group whose focus is to educate the public about the harm caused by drunk drivers.A study was recently done that emphasized the problem we all face with drinking and driving.Four hundred accidents that occurred on a Saturday night were analyzed.Two items noted were the number of vehicles involved and whether alcohol played a role in the accident.The numbers are shown below:
-Referring to Scenario 4-1, given that 3 vehicles were involved, what proportion of accidents involved alcohol?
A) 20 / 30 or 66.67%
B) 20 / 50 or 40%
C) 20 / 170 or 11.77%
D) 20 / 400 or 5%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
59
SCENARIO 4-2
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, what is the probability that a randomly selected student did well on the midterm and went bar hopping the weekend before the midterm?
A) 30 / 200 or 15%
B) (80+30) / 200 or 55%
C) (30+70) / 200 or 50%
D) (80+30+70) / 200 or 90%
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, what is the probability that a randomly selected student did well on the midterm and went bar hopping the weekend before the midterm?
A) 30 / 200 or 15%
B) (80+30) / 200 or 55%
C) (30+70) / 200 or 50%
D) (80+30+70) / 200 or 90%

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
60
SCENARIO 4-2
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, the events "Did Well on Midterm" and "Did Poorly on Midterm" are
A)dependent.
B)mutually exclusive.
C)collective exhaustive.
D)All the above.
An alcohol awareness task force at a Big-Ten university sampled 200 students after the midterm to ask them whether they went bar hopping the weekend before the midterm or spent the weekend studying, and whether they did well or poorly on the midterm.The following result was obtained.
-Referring to Scenario 4-2, the events "Did Well on Midterm" and "Did Poorly on Midterm" are
A)dependent.
B)mutually exclusive.
C)collective exhaustive.
D)All the above.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
61
If P (A and B) = 1, then A and B must be collectively exhaustive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
62
If P (A and B) = 1, then A and B must be mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
63
If , then A and B must be collectively exhaustive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
64
SCENARIO 4-3
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is a child or prefers hamburger is .
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is a child or prefers hamburger is .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
65
, then A and B must be collectively exhaustive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
66
Suppose A and B are mutually exclusive events where P(A) = 0.4 and P(B) = 0.5.Then P (A orB) = .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
67
If P(A) = 0.4 and P(B) = 0.6, then A and B must be mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
68
SCENARIO 4-3
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is an adult is.
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is an adult is.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
69
If P (A or B) = 1.0, then A and B must be mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
70
SCENARIO 4-3
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is an adult and prefers chicken is .
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is an adult and prefers chicken is .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
71
Suppose A and B are independent events where P(A) = 0.4 and P(B) = 0.5.Then P (A and B) =.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
72
Suppose A and B are events where P(A) = 0.4, P(B) = 0.5, and P (A and B) = 0.1. 


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
73
SCENARIO 4-3
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is a child and prefers chicken is .
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is a child and prefers chicken is .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
74
If , then A and B must be mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose A and B are independent events where P(A) = 0.4 and P(B) = 0.5.Then P (A or B) =.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
76
SCENARIO 4-3
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is an adult, or a child is .
A survey is taken among customers of a fast-food restaurant to determine preference for hamburger or chicken.Of 200 respondents selected, 75 were children and 125 were adults.120 preferred hamburger and 80 preferred chicken.55 of the children preferred hamburger.
Referring to Scenario 4-3, the probability that a randomly selected individual is an adult, or a child is .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
77
Suppose A and B are mutually exclusive events where P(A) = 0.4 and P(B) = 0.5.Then P (A andB) = .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose A and B are events where 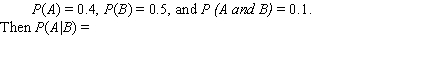 .
.
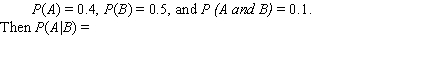 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose A and B are events where P(A) = 0.4, P(B) = 0.5, and P (A and B) = 0.1.Then P (A or B) = .

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
80
If P (A or B) = 1.0, then A and B must be collectively exhaustive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck


