Deck 10: Two-Sample Tests

Question 1

SCENARIO 10-1
Are Japanese managers more motivated than American managers? A randomly selected group of each were administered the Sarnoff Survey of Attitudes Toward Life (SSATL), which measures motivation for upward mobility.The SSATL scores are summarized below. $$\begin{array} { l l l } & \text { American } & \text { Japanese } \\\text { Sample Size } & 211 & 100 \\\text { Sample Mean SSATL Score } & 65.75 & 79.83 \\\text { Sample Std. Dev. } & 11.07 & 6.41\end{array}$$

-Referring to Scenario 10-1, what is the value of the test statistic?

A)-14.08
B)-11.8092
C)-1.9677
D)96.4471

Answer 1

-11.8092

Question 2

SCENARIO 10-1
Are Japanese managers more motivated than American managers? A randomly selected group of each were administered the Sarnoff Survey of Attitudes Toward Life (SSATL), which measures motivation for upward mobility.The SSATL scores are summarized below. $$\begin{array} { l l l } & \text { American } & \text { Japanese } \\\text { Sample Size } & 211 & 100 \\\text { Sample Mean SSATL Score } & 65.75 & 79.83 \\\text { Sample Std. Dev. } & 11.07 & 6.41\end{array}$$

-Referring to Scenario 10-1, find the p-value if we assume that the alternative hypothesis was a two-tail test.

A)Smaller than 0.01
B)Between 0.01 and 0.05
C)Between 0.05 and 0.10
D)Greater than 0.10

Answer 2

Smaller than 0.01

Question 3

In testing for differences between the means of two independent populations, the null hypothesis is:

A) $H _ { 0 } : \mu _ { 1 } - \mu _ { 2 } = 2$
B) $H _ { 0 } : \mu _ { 1 } - \mu _ { 2 } = 0 .$
C) $H _ { 0 } : \mu _ { 1 } - \mu _ { 2 } > 0$
D) $H _ { 0 } : \mu _ { 1 } - \mu _ { 2 } < 2$

Answer 3

$H _ { 0 } : \mu _ { 1 } - \mu _ { 2 } = 0 .$

Question 4

The sample size in each independent sample must be the same if we are to test for differences between the means of two independent populations.

Question 5

Given the following information, calculate sp2, the pooled sample variance that should be used in the pooled-variance t test.
$\begin{array} { l l } s _ { 1 } { } ^ { 2 } 4 & s _ { 2 } { } ^ { 2 } = 6 \\n _ { 1 } = 16 & m _ { 2 } = 25\end{array}$

A) $s _ { p } ^ { 2 } = 6.00$
B) $s _ { p } ^ { 2 } = 5.00$
C) $s _ { p } ^ { 2 } = 5.23$
D) $s _ { p } ^ { 2 } = 4.00$

Question 6

For all two-sample tests, the sample sizes must be equal in the two groups.

Question 7

The t test for the difference between the means of 2 independent populations assumes that the respective

A)sample sizes are equal.
B)sample variances are equal.
C)populations are approximately normal.
D)All the above.

Question 8

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, the researcher was attempting to show statistically that the female MBA graduates have a significantly lower mean starting salary than the male MBA graduates.From the analysis in Scenario 10-2, the correct test statistic is:

A)-6610
B)-1.3763
C)-1.7011
D)0.0898

Question 9

SCENARIO 10-1
Are Japanese managers more motivated than American managers? A randomly selected group of each were administered the Sarnoff Survey of Attitudes Toward Life (SSATL), which measures motivation for upward mobility.The SSATL scores are summarized below. $$\begin{array} { l l l } & \text { American } & \text { Japanese } \\\text { Sample Size } & 211 & 100 \\\text { Sample Mean SSATL Score } & 65.75 & 79.83 \\\text { Sample Std. Dev. } & 11.07 & 6.41\end{array}$$

-Referring to Scenario 10-1, give the null and alternative hypotheses to determine if the meanSSATL score of Japanese managers differs from the mean SSATL score of American managers.

A) $H _ { 0 } : \mu _ { A } - \mu _ { J } \geq 0 \text { versus } H _ { 1 } : \mu _ { A } - \mu _ { J } < 0$
B) $H _ { 0 } : \mu _ { A } - \mu _ { J } \leq 0 \text { versus } H _ { 1 } : \mu _ { A } - \mu _ { J } > 0$
C) $H _ { 0 } : \mu _ { A } - \mu _ { J } = 0 \text { versus } H _ { 1 } : \mu _ { A } - \mu _ { J } \neq 0$
D) $H _ { 0 } : \bar { X } _ { A } - \bar { X } _ { J } = 0 \text { versus } H _ { 1 } : \bar { X } _ { A } - \bar { X } _ { J } \neq 0$

Question 10

In testing for the differences between the means of two independent populations, you assume that the 2 populations each follow a distribution.

Question 11

When you test for differences between the means of two independent populations, you can only use a two-tail test.

Question 12

A statistics professor wanted to test whether the grades on a statistics test were the same for upper and lower classmen.The professor took a random sample of size 10 from each, conducted a test and found out that the variances were equal.For this situation, the professor should use a t test with related samples.

Question 13

In testing for the differences between the means of 2 independent populations where the variances in each population are unknown but assumed equal, the degrees of freedom are

A)n - 1.
B)n1 + n2 - 1.
C)n1 + n2 - 2.
D)n - 2.

Question 14

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, the researcher was attempting to show statistically that the female MBA graduates have a significantly lower mean starting salary than the male MBA graduates.The proper conclusion for this test is:

A)At the $\alpha$ = 0.10 level, there is sufficient evidence to indicate a difference in the mean starting salaries of male and female MBA graduates.
B)At the $\alpha$ = 0.10 level, there is sufficient evidence to indicate that females have a lower mean starting salary than male MBA graduates.
C)At the $\alpha$ = 0.10 level, there is sufficient evidence to indicate that females have a higher mean starting salary than male MBA graduates.
D)At the $\alpha$ = 0.10 level, there is insufficient evidence to indicate any difference in the mean starting salaries of male and female MBA graduates.

Question 15

SCENARIO 10-1
Are Japanese managers more motivated than American managers? A randomly selected group of each were administered the Sarnoff Survey of Attitudes Toward Life (SSATL), which measures motivation for upward mobility.The SSATL scores are summarized below. $$\begin{array} { l l l } & \text { American } & \text { Japanese } \\\text { Sample Size } & 211 & 100 \\\text { Sample Mean SSATL Score } & 65.75 & 79.83 \\\text { Sample Std. Dev. } & 11.07 & 6.41\end{array}$$

-Referring to Scenario 10-1, judging from the way the data were collected, which test would likely be most appropriate to employ?

A)Paired t test
B)Pooled-variance t test for the difference between two means
C)F test for the ratio of two variances
D)Z test for the difference between two proportions

Question 16

Given the following information, calculate the degrees of freedom that should be used in the pooled-variance t test.

$$\begin{array} { l l } s _ { 1 } ^ { 2 } = 4 & s _ { 2 } ^ { 2 } = 6 \\n _ { 1 } = 16 & n _ { 2 } = 25\end{array}$$

A) df = 41
B) df = 39
C) df = 16
D) df = 25

Question 17

When the sample sizes are equal, the pooled variance of the two groups is the average of the 2 sample variances.

Question 18

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, the researcher was attempting to show statistically that the female MBA graduates have a significantly lower mean starting salary than the male MBA graduates.Which of the following is an appropriate alternative hypothesis?

A) $H _ { 1 } : \mu _ { \text {females } } > \mu _ { \text {males } }$
B) $H _ { 1 } : \mu _ { \text {females } } < \mu _ { \text {males } }$
C) $H _ { 1 } : \mu _ { \text {females } } \neq \mu _ { \text {males } }$
D) $H _ { 1 } : \mu _ { \text {females } } = \mu _ { \text {males } }$

Question 19

A statistics professor wanted to test whether the grades on a statistics test were the same for upper and lower classmen.The professor took a random sample of size 10 from each, conducted a test and found out that the variances were equal.For this situation, the professor should use a t test with independent samples.

Question 20

If we are testing for the difference between the means of 2 independent populations presuming equal variances with samples of n1 = 20 and n2 = 20, the number of degrees of freedom is equal to

A)39.
B)38.
C)19.
D)18.

Question 21

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is the 95% confidence interval estimate for the difference in the two means?

Question 22

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, the researcher was attempting to show statistically that the female MBA graduates have a significantly lower mean starting salary than the male MBA graduates.What assumptions were necessary to conduct this hypothesis test?

A)Both populations of salaries (male and female)must have approximate normal distributions.
B)The population variances are approximately equal.
C)The samples were randomly and independently selected.
D)All of the above assumptions were necessary.

Question 23

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is a point estimate for the mean of the sampling distribution of the difference between the 2-sample means?

A)- 22
B)- 10
C)- 15
D)0

Question 24

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, suppose $\alpha$ = 0.10.Which of the following represents the correct conclusion?

A)There is not enough evidence that the mean amount of time families in Gotham have been living in their current homes is less than families in Metropolis.
B)There is enough evidence that the mean amount of time families in Gotham have been living in their current homes is less than families in Metropolis.
C)There is not enough evidence that the mean amount of time families in Gotham have been living in their current homes is not less than families in Metropolis.
D)There is enough evidence that the mean amount of time families in Gotham have been living in their current homes is not less than families in Metropolis.

Question 25

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, what is the 99% confidence interval estimate for the difference between two means?

Question 26

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is(are) the critical value(s) of the relevant hypothesis test if the level of significance is 0.01?

A) $t \cong Z = - 1.96$
B) $t \cong Z = \pm 1.96$
C) $t \cong Z = - 2.080$
D) $t \cong Z = - 2.33$

Question 27

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, suppose $\alpha$ = 0.01.Which of the following represents the result of the relevant hypothesis test?

A)The alternative hypothesis is rejected.
B)The null hypothesis is rejected.
C)The null hypothesis is not rejected.
D)Insufficient information exists on which to decide.

Question 28

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, which of the following represents the relevant hypotheses tested by the real estate company?

A) $H _ { 0 } : \mu _ { G } - \mu _ { M } \geq 0 \text { versus } H _ { 1 } : \mu _ { G } - \mu _ { M } < 0$
B) $H _ { 0 } : \mu _ { G } - \mu _ { M } \leq 0 \text { versus } H _ { 1 } : \mu _ { G } - \mu _ { M } > 0$
C) $H _ { 0 } : \mu _ { g } - \mu _ { M } = 0 \text { versus } H _ { 1 } : \mu _ { q } - \mu _ { M } \neq 0$
D) $H _ { 0 } : \bar { X } _ { G } - \bar { X } _ { M } \geq 0 \text { versus } H _ { 1 } : \bar { X } _ { G } - \bar { X } _ { M } < 0$

Question 29

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is the estimated standard error of the difference between the 2- sample means?

A)4.06
B)5.61
C)8.01
D)16.00

Question 30

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is the test statistic for the difference between sample means?

A)- 8.75
B)- 3.69
C)- 2.33
D)- 1.96

Question 31

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, what is the 90% confidence interval estimate for the difference between two means?

Question 32

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, suppose $\alpha$ = 0.05.Which of the following represents the correct conclusion?

A)There is not enough evidence that the mean amount of time families in Gotham have been living in their current homes is less than families in Metropolis.
B)There is enough evidence that the mean amount of time families in Gotham have been living in their current homes is less than families in Metropolis.
C)There is not enough evidence that the mean amount of time families in Gotham have been living in their current homes is not less than families in Metropolis.
D)There is enough evidence that the mean amount of time families in Gotham have been living in their current homes is not less than families in Metropolis.

Question 33

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is(are) the critical value(s) of the relevant hypothesis test if the level of significance is 0.05?

A) $t \cong Z = - 1.645$
B) $t \cong Z = \pm 1.96$
C) $t \cong Z = - 1.96$
D) $t \cong Z = - 2.080$

Question 34

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-4, the computed t statistic is .

Question 35

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, suppose $\alpha$ = 0.05.Which of the following represents the result of the relevant hypothesis test?

A)The alternative hypothesis is rejected.
B)The null hypothesis is rejected.
C)The null hypothesis is not rejected.
D)Insufficient information exists on which to decide.

Question 36

SCENARIO 10-2
A researcher randomly sampled 30 graduates of an MBA program and recorded data concerning their starting salaries.Of primary interest to the researcher was the effect of gender on starting salaries.
The result of the pooled-variance t-test of the mean salaries of the females (Population 1) and males
(Population 2) in the sample is given below. $\begin{array}{|l|r|}\hline \text { Hypothesized Difference } & 0 \\\hline \text { Level of Significance } & 0.05 \\\hline\text { Population 1 Sample }\\\hline \text { Sample Size } & 18 \\\hline \text { Sample Mean } & 99210 \\\hline \text { Sample Standard Deviation } & 13577 \\\text { Population 2 Sample } \\\hline \text { Sample Size } & 12 \\\hline \text { Sample Mean } & 105820 \\\hline \text { Sample Standard Deviation } & 11741 \\\hline\\\hline \text { Difference in Sample Means } & -6610 \\\hline t \text { Test Statistic } & -1.37631 \\\hline\\\hline {\text { Lower-Tail Test }} \\\hline \text { Lower Critical Value } & -1.70113 \\\hline \text { p-Value } & 0.089816 \\\hline\end{array}$

-Referring to Scenario 10-2, what is the 95% confidence interval estimate for the difference between two means?

Question 37

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-6, the pooled (i.e., combined) variance is .

Question 38

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, suppose $\alpha$ = 0.01.Which of the following represents the correct conclusion?

A)There is not enough evidence that the mean amount of time families in Gotham have been living in their current homes is less than families in Metropolis.
B)There is enough evidence that the mean amount of time families in Gotham have been living in their current homes is less than families in Metropolis.
C)There is not enough evidence that the mean amount of time families in Gotham have been living in their current homes is not less than families in Metropolis.
D)There is enough evidence that the mean amount of time families in Gotham have been living in their current homes is not less than families in Metropolis.

Question 39

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, what is the 99% confidence interval estimate for the difference in the two means?

Question 40

SCENARIO 10-3
A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis.Assume that the two population variances are equal.A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes.
Gotham:
$$\bar { X } _ { \mathrm { G } } = 35 \text { months, } \quad S _ { \mathrm { G } } { } ^ { 2 } = 900 \quad \text { Metropolis: } \quad \bar { X } _ { \mathrm { M } } = 50 \text { months, } \mathrm { S } _ { \mathrm { M } } { } ^ { 2 } = 1050$$

-Referring to Scenario 10-3, suppose $\alpha$ = 0.10.Which of the following represents the result of the relevant hypothesis test?

A)The alternative hypothesis is rejected.
B)The null hypothesis is rejected.
C)The null hypothesis is not rejected.
D)Insufficient information exists on which to decide.

Question 41

A researcher is curious about the effect of sleep on students' test performances.He chooses 60 students and gives each two tests: one given after two hours' sleep and one after eight hours' sleep.The test the researcher should use would be a related samples test.

Question 42

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.

-Referring to Scenario 10-4, the critical values for a two-tail test of the null hypothesis of no difference in the population means at the $\alpha$ = 0.05 level of significance are .

Question 43

In what type of test is the variable of interest the difference between the values of the observations rather than the observations themselves?

A)A test for the equality of variances from 2 independent populations.
B)A test for the difference between the means of 2 related populations.
C)A test for the difference between the means of 2 independent populations.
D)All of the above.

Question 44

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.

-Referring to Scenario 10-4, if you were interested in testing against the one-tail alternative that $\mu$ 1 $\gt$ $\mu$ 2 at the $\alpha$ = 0.01 level of significance, the null hypothesis would (be rejected/notbe rejected).

Question 45

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-4, the p-value for a two-tail test is _.

Question 46

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.

-Referring to Scenario 10-4, what is the 99% confidence interval estimate for the difference in the two means?

Question 47

When testing for differences between the means of 2 related populations, you can use either a one-tail or two-tail test.

Question 48

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-4, what is the 90% confidence interval estimate for the difference in the two means?

Question 49

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-4, there are degrees of freedom for this test.

Question 50

If we are testing for the difference between the means of 2 related populations with samples of n1= 20 and n2 = 20, the number of degrees of freedom is equal to

A)39.
B)38.
C)19.
D)18.

Question 51

In testing for the differences between the means of two related populations, thehypothesis is the hypothesis of "no differences."

Question 52

In testing for differences between the means of 2 related populations where the variance of the differences is unknown, the degrees of freedom are

A) $n - 1$
B) $n _ { 1 } + n _ { 2 } - 1.$
C) $n _ { 1 } + n _ { 2 } - 2.$
D) $n - 2.$

Question 53

Repeated measurements from the same individuals is an example of data collected from two related populations.

Question 54

In testing for differences between the means of two related populations, the null hypothesis is

A) $H _ { 0 } : \mu _ { D } = 2.$
B) $H _ { 0 } : \mu _ { D } = 0.$
C) $H _ { 0 } : \mu _ { D } < 0.$
D) $H _ { 0 } : \mu _ { D } > 0.$

Question 55

A Marine drill instructor recorded the time in which each of 11 recruits completed an obstacle course both before and after basic training.To test whether any improvement occurred, the instructor would use a t-distribution with 11 degrees of freedom.

Question 56

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.

-Referring to Scenario 10-4, a two-tail test of the null hypothesis of no difference would (be rejected/not be rejected) at the $\alpha$ = 0.05 level of significance.

Question 57

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-4, what is the 95% confidence interval estimate for the difference in the two means?

Question 58

In testing for the differences between the means of two related populations, you assume that the differences follow a distribution.

Question 59

The t test for the mean difference between 2 related populations assumes that the

A)population sizes are equal.
B)sample variances are equal.
C)population of differences is approximately normal, or sample sizes are large enough.
D)All of the above.

Question 60

SCENARIO 10-4
Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances.The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0.
Referring to Scenario 10-4, the p-value for a one-tail test (in the hypothesized direction) is.

Question 61

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, you must assume that the population of difference scores is normally distributed.

Question 62

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.
Referring to Scenario 10-6, the p-value for a two-tail is .

Question 63

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.

-Referring to Scenario 10-6, a one-tail test of the null hypothesis of no difference would (be rejected/not be rejected) at the $\alpha$ = 0.05 level of significance.

Question 64

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, the value of the sample mean difference is if the difference scores reflect the results of the exam after the course minus the results of the exam before the course.

A)0
B)50
C)68
D)400

Question 65

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.
Referring to Scenario 10-6, the t test should be -tail.

Question 66

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below.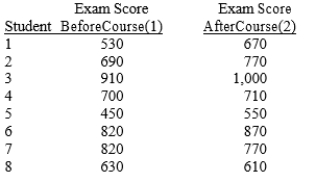
Referring to Scenario 10-5, the p-value of the test statistic is .

Question 67

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, what is the critical value for testing at the 5% level of significance whether the business school preparation course is effective in improving exam scores?

A)2.365
B)2.145
C)1.761
D)1.895

Question 68

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.
Referring to Scenario 10-6, the computed t statistic is .

Question 69

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.

-Referring to Scenario 10-6, what is the 95% confidence interval estimate for the mean difference in weight before and after the diet?

Question 70

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below.
Referring to Scenario 10-5, the calculated value of the test statistic is _.

Question 71

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, the value of the standard error of the difference scores is

A)65.027
B)60.828
C)22.991
D)14.696

Question 72

A Marine drill instructor recorded the time in which each of 11 recruits completed an obstacle course both before and after basic training.To test whether any improvement occurred, the instructor would use a t-distribution with 10 degrees of freedom.

Question 73

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.

-Referring to Scenario 10-6, the critical value for a one-tail test of the null hypothesis of no difference at the $\alpha$ = 0.05 level of significance is .

Question 74

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, at the 0.05 level of significance, the conclusion for this hypothesis test is that there is sufficient evidence that:

A)the business school preparation course does improve exam score.
B)the business school preparation course does not improve exam score.
C)the business school preparation course has no impact on exam score.
D)no conclusion can be drawn from the information given.

Question 75

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.
Referring to Scenario 10-6, there are degrees of freedom for this test.

Question 76

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, at the 0.05 level of significance, the decision for this hypothesis test would be:

A)reject the null hypothesis.
B)do not reject the null hypothesis.
C)reject the alternative hypothesis.
D)It cannot be determined from the information given.

Question 77

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, the number of degrees of freedom is

A)14.
B)13.
C)8.
D)7.

Question 78

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.
Referring to Scenario 10-6, the p-value for a one-tail test is _.

Question 79

SCENARIO 10-6
To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet.The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later.Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t-test for related samples can be used to determine if there was a significant decrease in the mean weight during this period.Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds.

-Referring to Scenario 10-6, if we were interested in testing against the two-tail alternative that $\mu$ D is not equal to zero at the $\alpha$ = 0.05 level of significance, the null hypothesis would (be rejected/not be rejected).

Question 80

SCENARIO 10-5
To test the effectiveness of a business school preparation course, 8 students took a general business test before and after the course.The results are given below. $$\begin{array} { l c c } \text { Student } & \begin{array} { c } \text { Exam Score } \\\text { BeforeCourse(1) }\end{array} & \begin{array} { c } \text { Exam Score } \\\text { AfterCourse(2) }\end{array} \\\hline 1 & 530 & 670 \\2 & 690 & 770 \\3 & 910 & 1,000 \\4 & 700 & 710 \\5 & 450 & 550 \\6 & 820 & 870 \\7 & 820 & 770 \\8 & 630 & 610\end{array}$$

-Referring to Scenario 10-5, in examining the differences between related samples we are essentially sampling from an underlying population of difference "scores."