Deck 13: Multiple Regression

Question 1

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, the p-value for GDP is

A)0.05
B)0.01
C)0.001
D)None of the above.

Answer 1

None of the above.

Question 2

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, what is the predicted consumption level for an economy withGDP equal to $4 billion and an aggregate price index of 150?

A)$1.39 billion
B)$2.89 billion
C)$4.75 billion
D)$9.45 billion

Answer 2

$2.89 billion

Question 3

In a multiple regression problem involving two independent variables, if b1 is computed to be+2.0, it means that

A)the relationship between X1 and Y is significant.
B)the estimated mean of Y increases by 2 units for each increase of 1 unit of X1, holding X2 constant.
C)the estimated mean of Y increases by 2 units for each increase of 1 unit of X1, without regard to X2.
D)the estimated mean of Y is 2 when X1 equals zero.

Answer 3

B

Question 4

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, what is the estimated mean consumption level for an economy with GDP equal to $4 billion and an aggregate price index of 150?

A)$1.39 billion
B)$2.89 billion
C)$4.75 billion
D)$9.45 billion

Question 5

SCENARIO 13-2
A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2).The professor randomly selects 6 workers and collects the following information: $$\begin{array} { c c r r } \text { Employee } & { Y ( \$ ) } & \underline { X } _ { 1 } & X _ { 2 } \\1 & 10 & 3 & 0 \\2 & 12 & 1 & 5 \\3 & 15 & 8 & 1 \\4 & 17 & 5 & 8 \\5 & 20 & 7 & 12 \\6 & 25 & 10 & 9\end{array}$$

-Referring to SCENARIO 13-2, an employee who took 12 economics courses scores 10 on the performance rating.What is her estimated expected wage rate?

A)10.90
B)12.20
C)24.87
D)25.70

Question 6

SCENARIO 13-2
A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2).The professor randomly selects 6 workers and collects the following information: $$\begin{array} { c c r r } \text { Employee } & { Y ( \$ ) } & \underline { X } _ { 1 } & X _ { 2 } \\1 & 10 & 3 & 0 \\2 & 12 & 1 & 5 \\3 & 15 & 8 & 1 \\4 & 17 & 5 & 8 \\5 & 20 & 7 & 12 \\6 & 25 & 10 & 9\end{array}$$

-Referring to SCENARIO 13-2, suppose an employee had never taken an economics course and managed to score a 5 on his performance rating.What is his estimated expected wage rate?

A)10.90
B)12.20
C)17.23
D)25.11

Question 7

SCENARIO 13-2
A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2).The professor randomly selects 6 workers and collects the following information: $$\begin{array} { c c r r } \text { Employee } & { Y ( \$ ) } & \underline { X } _ { 1 } & X _ { 2 } \\1 & 10 & 3 & 0 \\2 & 12 & 1 & 5 \\3 & 15 & 8 & 1 \\4 & 17 & 5 & 8 \\5 & 20 & 7 & 12 \\6 & 25 & 10 & 9\end{array}$$

-Referring to SCENARIO 13-2, for these data, what is the value for the regression constant, b0?

A)0.616
B)1.054
C)6.932
D)9.103

Question 8

The variation attributable to factors other than the relationship between the independent variables and the explained variable in a regression analysis is represented by

A)regression sum of squares.
B)error sum of squares.
C)total sum of squares.
D)regression mean squares.

Question 9

SCENARIO 13-2
A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2).The professor randomly selects 6 workers and collects the following information: $$\begin{array} { c c r r } \text { Employee } & { Y ( \$ ) } & \underline { X } _ { 1 } & X _ { 2 } \\1 & 10 & 3 & 0 \\2 & 12 & 1 & 5 \\3 & 15 & 8 & 1 \\4 & 17 & 5 & 8 \\5 & 20 & 7 & 12 \\6 & 25 & 10 & 9\end{array}$$

-Referring to SCENARIO 13-2, for these data, what is the estimated coefficient for performance rating, b1?

A)0.616
B)1.054
C)6.932
D)9.103

Question 10

In a multiple regression model, the value of the coefficient of multiple determination

A)has to fall between -1 and +1.
B)has to fall between 0 and +1.
C)has to fall between -1 and 0.
D)can fall between any pair of real numbers.

Question 11

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, the p-value for the aggregated price index is

A)0.05
B)0.01
C)0.001
D)None of the above.

Question 12

SCENARIO 13-1
A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X1) and how he/she scored on a business aptitude test (X2).A random sample of 8 employees provides the following: $$\begin{array} { c r r r } \text { Emplovee } & { Y } & { X _ { 1 } } & X _ { 2 } \\\hline 1 & 100 & 10 & 7 \\2 & 90 & 3 & 10 \\3 & 80 & 8 & 9 \\4 & 70 & 5 & 4 \\5 & 60 & 5 & 8 \\6 & 50 & 7 & 5 \\7 & 40 & 1 & 4 \\8 & 30 & 1 & 1\end{array}$$

-Referring to SCENARIO 13-1, if an employee who had been with the company 5 years scored a 9 on the aptitude test, what would his estimated expected sales be?

A)79.09
B)60.88
C)55.62
D)17.98

Question 13

In a multiple regression model, which of the following is correct regarding the value of the adjusted r 2 ?

A)It can be negative.
B)It has to be positive.
C)It has to be larger than the coefficient of multiple determination.
D)It can be larger than 1.

Question 14

SCENARIO 13-1
A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X1) and how he/she scored on a business aptitude test (X2).A random sample of 8 employees provides the following: $$\begin{array} { c r r r } \text { Emplovee } & { Y } & { X _ { 1 } } & X _ { 2 } \\\hline 1 & 100 & 10 & 7 \\2 & 90 & 3 & 10 \\3 & 80 & 8 & 9 \\4 & 70 & 5 & 4 \\5 & 60 & 5 & 8 \\6 & 50 & 7 & 5 \\7 & 40 & 1 & 4 \\8 & 30 & 1 & 1\end{array}$$

-Referring to SCENARIO 13-1, for these data, what is the estimated coefficient for the variable representing scores on the aptitude test, b2?

A)0.998
B)3.103
C)4.698
D)21.293

Question 15

SCENARIO 13-2
A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2).The professor randomly selects 6 workers and collects the following information: $$\begin{array} { c c r r } \text { Employee } & { Y ( \$ ) } & \underline { X } _ { 1 } & X _ { 2 } \\1 & 10 & 3 & 0 \\2 & 12 & 1 & 5 \\3 & 15 & 8 & 1 \\4 & 17 & 5 & 8 \\5 & 20 & 7 & 12 \\6 & 25 & 10 & 9\end{array}$$

-Referring to SCENARIO 13-2, for these data, what is the estimated coefficient for the number of economics courses taken, b2?

A)0.616
B)1.054
C)6.932
D)9.103

Question 16

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, the p-value for the regression model as a whole is

A)0.05
B)0.01
C)0.001
D)None of the above.

Question 17

SCENARIO 13-1
A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X1) and how he/she scored on a business aptitude test (X2).A random sample of 8 employees provides the following: $$\begin{array} { c r r r } \text { Emplovee } & { Y } & { X _ { 1 } } & X _ { 2 } \\\hline 1 & 100 & 10 & 7 \\2 & 90 & 3 & 10 \\3 & 80 & 8 & 9 \\4 & 70 & 5 & 4 \\5 & 60 & 5 & 8 \\6 & 50 & 7 & 5 \\7 & 40 & 1 & 4 \\8 & 30 & 1 & 1\end{array}$$

-Referring to SCENARIO 13-1, for these data, what is the estimated coefficient for the variable representing years an employee has been with the company, b1?

A)0.998
B)3.103
C)4.698
D)21.293

Question 18

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, when the economist used a simple linear regression model with consumption as the dependent variable and GDP as the independent variable, he obtained an r2 value of 0.971.What additional percentage of the total variation of consumption has been explained by including aggregate prices in the multiple regression?

A)98.2
B)11.1
C)2.8
D)1.1

Question 19

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, what is the estimated mean consumption level for an economy with GDP equal to $2 billion and an aggregate price index of 90?

A)$1.39 billion
B)$2.89 billion
C)$4.75 billion
D)$9.45 billion

Question 20

SCENARIO 13-1
A manager of a product sales group believes the number of sales made by an employee (Y) depends on how many years that employee has been with the company (X1) and how he/she scored on a business aptitude test (X2).A random sample of 8 employees provides the following: $$\begin{array} { c r r r } \text { Emplovee } & { Y } & { X _ { 1 } } & X _ { 2 } \\\hline 1 & 100 & 10 & 7 \\2 & 90 & 3 & 10 \\3 & 80 & 8 & 9 \\4 & 70 & 5 & 4 \\5 & 60 & 5 & 8 \\6 & 50 & 7 & 5 \\7 & 40 & 1 & 4 \\8 & 30 & 1 & 1\end{array}$$

-Referring to SCENARIO 13-1, for these data, what is the value for the regression constant, b0?

A)0.998
B)3.103
C)4.698
D)21.293

Question 21

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, one economy in the sample had an aggregate consumption level of $4 billion, a GDP of $6 billion, and an aggregate price level of 200.What is the residual for this data point?

A)$4.39 billion
B)$0.39 billion
C)- $0.39 billion
D)- $1.33 billion

Question 22

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, which of the following values for the level of significance is the smallest for which the regression model as a whole is significant?

A)0.0005
B)0.001
C)0.01
D)0.05

Question 23

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, to test whether aggregate price index has a positive impact on consumption, the p-value is

A)0.0001
B)0.4165
C)0.5835
D)0.8330

Question 24

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, to test whether gross domestic product has a positive impact on consumption, the p-value is

A)0.00005
B)0.0001
C)0.9999
D)0.99995

Question 25

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, to test for the significance of the coefficient on aggregate price index, the p-value is

A)0.0001
B)0.8330
C)0.8837
D)0.9999

Question 26

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, one individual in the sample had an annual income of $100,000 and a family size of 10.This individual owned a home with an area of 7,000 square feet (House =70.00).What is the residual (in hundreds of square feet) for this data point?

Question 27

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, what annual income (in thousands of dollars) would an individual with a family size of 4 need to attain a predicted 10,000 square foot home (House = 100)?

Question 28

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, which of the following values for the level of significance is the smallest for which each explanatory variable is significant individually?

A)0.001
B)0.010
C)0.025
D)0.050

Question 29

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, when the builder used a simple linear regression model with house size (House) as the dependent variable and family size (Size) as the independent variable, he obtained an r2 value of 1.25%.What additional percentage of the total variation in house size has been explained by including income in the multiple regression?

A)15.00%
B)70.64%
C)71.50%
D)73.62%

Question 30

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, which of the following values for the level of significance is the smallest for which at most one explanatory variable is significant individually?

A)0.001
B)0.010
C)0.025
D)0.050

Question 31

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, to test for the significance of the coefficient on gross domestic product, the p-value is

A)0.0001
B)0.8330
C)0.8837
D)0.9999

Question 32

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, what fraction of the variability in house size is explained by income and size of family?

A)17.56%
B)70.69%
C)71.89%
D)84.79%

Question 33

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, to test for the significance of the coefficient on aggregate price, the value of the relevant t-statistic is

A)2.365
B)0.143
C)- 0.219
D)- 1.960

Question 34

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, what is the predicted house size (in hundreds of square feet) for an individual earning an annual income of $40,000 and having a family size of 4?

Question 35

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, what annual income (in thousands of dollars) would an individual with a family size of 9 need to attain a predicted 5,000 square foot home (House = 50)?

Question 36

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, which of the following values for the level of significance is the smallest for which at least one explanatory variable is significant individually?

A)0.005
B)0.010
C)0.025
D)0.050

Question 37

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, which of the independent variables in the model are significant at the 5% level?

A)Income only
B)Size only
C)Income and Size
D)None

Question 38

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, one individual in the sample had an annual income of $40,000 and a family size of 1.This individual owned a home with an area of 1,000 square feet (House =10.00).What is the residual (in hundreds of square feet) for this data point?

Question 39

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, to test whether aggregate price index has a negative impact on consumption, the p-value is ?

A)0.0001
B)0.4165
C)0.8330
D)0.8837

Question 40

SCENARIO 13-3
An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. $\text { SUMMARY OUTPUT }$
$\begin{array}{ll}{\text { Regression Statistics }} \\\text { Multiple R } & 0.991 \\\text { R Square } & 0.982 \\\text { Adjusted R Square } & 0.976 \\\text { Standard Error } & 0.299 \\\text { Observations } & 10\end{array}$

ANOVA
$\begin{array}{lccccc} & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\\text { Regression } & 2 & 33.4163 & 16.7082 & 186.325 & 0.0001 \\\text { Residual } & 7 & 0.6277 & 0.0897 & & \\\text { Total } & 9 & 34.0440 & & &\end{array}$

$\begin{array}{lclcc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & -0.0861 & 0.5674 & -0.152 & 0.8837 \\\text { GDP } & 0.7654 & 0.0574 & 13.340 & 0.0001 \\\text { Price } & -0.0006 & 0.0028 & -0.219 & 0.8330\end{array}$

-Referring to SCENARIO 13-3, one economy in the sample had an aggregate consumption level of $3 billion, a GDP of $3.5 billion, and an aggregate price level of 125.What is the residual for this data point?

A)$2.52 billion
B)$0.48 billion
C)- $1.33 billion
D)- $2.52 billion

Question 41

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, what are the regression degrees of freedom that are missing from the output?

A)2
B)47
C)49
D)50

Question 42

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, the partial F test forH0: Variable X1 does not significantly improve the model after variable X2 has been includedH1: Variable X1 significantly improves the model after variable X2 has been included has and degrees of freedom.

Question 43

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, _% of the variation in the house size can be explained by the variation in the family size while holding the family income constant.

Question 44

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, what is the value of the calculated F test statistic that is missing from the output for testing whether the whole regression model is significant?

Question 45

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, the partial F test forH0: Variable X2 does not significantly improve the model after variable X1 has been includedH1: Variable X2 significantly improves the model after variable X1 has been included has and degrees of freedom.

Question 46

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what is the p-value for Wages?

A)0.01
B)0.05
C)0.0001
D)None of the above

Question 47

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, the value of the partial F test statistic is forH0: Variable X1 does not significantly improve the model after variable X2 has been includedH1: Variable X1 significantly improves the model after variable X2 has been included

Question 48

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, at the 0.01 level of significance, what conclusion should the builder draw regarding the inclusion of Size in the regression model?

A)Size is significant in explaining house size and should be included in the model because its p-value is less than 0.01.
B)Size is significant in explaining house size and should be included in the model because its p-value is more than 0.01.
C)Size is not significant in explaining house size and should not be included in the model because its p-value is less than 0.01.
D)Size is not significant in explaining house size and should not be included in the model because its p-value is more than 0.01.

Question 49

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, which of the independent variables in the model are significant at the 5% level?

A)Capital, Wages
B)Capital
C)Wages
D)None of the above

Question 50

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, suppose the builder wants to test whether the coefficient onIncome is significantly different from 0.What is the value of the relevant t-statistic?

A)-0.7630
B)3.2708
C)10.8668
D)60.0864

Question 51

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what fraction of the variability in sales is explained by spending on capital and wages?

A)27.0%
B)50.9%
C)68.9%
D)83.0%

Question 52

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, the value of the partial F test statistic is forH0: Variable X2 does not significantly improve the model after variable X1 has been includedH1: Variable X2 significantly improves the model after variable X1 has been included

Question 53

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, the observed value of the F-statistic is missing from the printout.What are the degrees of freedom for this F-statistic?

A)2 for the numerator, 47 for the denominator
B)2 for the numerator, 49 for the denominator
C)49 for the numerator, 47 for the denominator
D)47 for the numerator, 49 for the denominator

Question 54

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, at the 0.01 level of significance, what conclusion should the builder reach regarding the inclusion of Income in the regression model?

A)Income is significant in explaining house size and should be included in the model because its p-value is less than 0.01.
B)Income is significant in explaining house size and should be included in the model because its p-value is more than 0.01.
C)Income is not significant in explaining house size and should not be included in the model because its p-value is less than 0.01.
D)Income is not significant in explaining house size and should not be included in the model because its p-value is more than 0.01.

Question 55

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4 and allowing for a 1% probability of committing a type I error,what is the decision and conclusion for the test H: $\beta$ 1 $\beta$ 2=0 vs.H : At least one $\beta$ j $\neq$ 0, j- 1, 20 1 2 1 j?

A)Do not reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on house size.
B)Do not reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on house size.
C)Reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on house size.
D)Reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on house size.

Question 56

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, suppose the builder wants to test whether the coefficient on Size is significantly different from 0.What is the value of the relevant t-statistic?

A)-0.7630
B)3.2708
C)10.8668
D)60.0864

Question 57

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, when the microeconomist used a simple linear regression model with sales as the dependent variable and wages as the independent variable, she obtained an r2 value of 0.601.What additional percentage of the total variation of sales has been explained by including capital spending in the multiple regression?

A)60.1%
B)31.1%
C)22.9%
D)8.8%

Question 58

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8479 \\\text { R Square } & 0.7189 \\\text { Adjusted R Square } & 0.7069 \\\text { Standard Error } & 17.5571 \\\text { Observations } & 50 \\\hline\end{array}$
ANOVA
$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & &37043.3236 & 18521.6618 && 0.0000 \\\text { Residual } & &14487.7627 & 308.2503 & \\\text { Total } & 49 & 51531.0863\\\hline \end{array}$

$\begin{array}{lrrrr} & \text { Coefficients } & \text { Standard Error } & t \text { Stat } &{\text {-value }} \\\hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\\text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\\text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\end{array}$

$\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$

-Referring to SCENARIO 13-4, what are the residual degrees of freedom that are missing from the output?

A)2
B)47
C)49
D)50

Question 59

SCENARIO 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:
Referring to SCENARIO 13-4, _% of the variation in the house size can be explained by the variation in the family income while holding the family size constant.

Question 60

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what is the p-value for testing whether Wages have a positive impact on corporate sales?

A)0.01
B)0.05
C)0.0001
D)0.00005

Question 61

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, one company in the sample had sales of $21.439 billion (Sales =21,439).This company spent $300 million on capital and $700 million on wages.What is the residual (in millions of dollars) for this data point?

A)790.69
B)648.31
C)-648.31
D)-790.69

Question 62

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.5270 \\\text { R Square } & 0.2778 \\\text { Adjusted R Square } & 0.1928 \\\text { Standard Error } & 40.9107 \\\text { Observations } & 20 \\\hline\end{array}\\\text { ANOVA }\end{array}$$

$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\\text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\\text { Total } & 19 & 39395.6218 & &\\\hline \end{array}$
13-22 Multiple Regression $$\begin{array}{l}\begin{array} { l r r r r r r } \hline & \text { Coefficients } & { \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\\text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\\text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\\hline\end{array}\\\text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672\end{array}$$

-Referring to SCENARIO 13-6 and allowing for a 1% probability of committing a type I error,what is the decision and conclusion for the testH : $\beta$ 1-2= 0 vs.H : At least one $\beta$ j $\neq$ 0, j - 1, 20 1 2 1 j?

A)Do not reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on heating costs.
B)Do not reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on heating costs.
C)Reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on heating costs.
D)Reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on heating costs.

Question 63

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what is the p-value for testing whether Wages have a negative impact on corporate sales?

A)0.05
B)0.0001
C)0.00005
D)0.99995

Question 64

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, suppose the microeconomist wants to test whether the coefficient on Capital is significantly different from 0.What is the value of the relevant t-statistic?

A)0.609
B)2.617
C)4.804
D)25.432

Question 65

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model.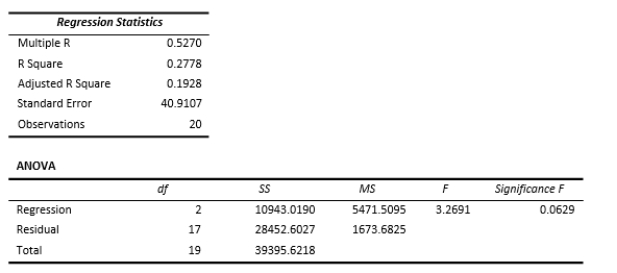 13-22 Multiple Regression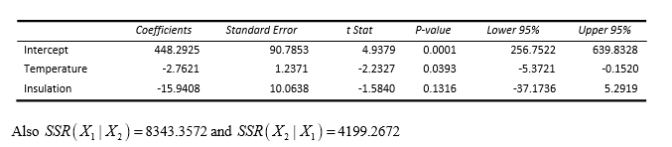
Referring to SCENARIO 13-6, the partial F test forH0: Variable X1 does not significantly improve the model after variable X2 has been includedH1: Variable X1 significantly improves the model after variable X2 has been included has and degrees of freedom.

Question 66

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what are the predicted sales (in millions of dollars) for a company spending $100 million on capital and $100 million on wages?

A)15,800.00
B)16,520.07
C)17,277.49
D)20,455.98

Question 67

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, at the 0.01 level of significance, what conclusion should the microeconomist reach regarding the inclusion of Capital in the regression model?

A)Capital is significant in explaining corporate sales and should be included in the model because its p-value is less than 0.01.
B)Capital is significant in explaining corporate sales and should be included in the model because its p-value is more than 0.01.
C)Capital is not significant in explaining corporate sales and should not be included in the model because its p-value is less than 0.01.
D)Capital is not significant in explaining corporate sales and should not be included in the model because its p-value is more than 0.01.

Question 68

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. 13-22 Multiple Regression
Referring to SCENARIO 13-6, the value of the partial F test statistic is forH0: Variable X1 does not significantly improve the model after variable X2 has been includedH1: Variable X1 significantly improves the model after variable X2 has been included

Question 69

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.5270 \\\text { R Square } & 0.2778 \\\text { Adjusted R Square } & 0.1928 \\\text { Standard Error } & 40.9107 \\\text { Observations } & 20 \\\hline\end{array}\\\text { ANOVA }\end{array}$$

$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\\text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\\text { Total } & 19 & 39395.6218 & &\\\hline \end{array}$
13-22 Multiple Regression $$\begin{array}{l}\begin{array} { l r r r r r r } \hline & \text { Coefficients } & { \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\\text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\\text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\\hline\end{array}\\\text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672\end{array}$$

-Referring to SCENARIO 13-6, what is the 95% confidence interval for the expected change in heating costs as a result of a 1 degree Fahrenheit change in the daily minimum outside temperature?

A)[256.7522, 639.8328]
B)[204.7854, 497.1733]
C)[-5.3721, -0.1520]
D)[-37.1736, 5.2919]

Question 70

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what is the p-value for testing whether Capital has a positive influence on corporate sales?

A)0.025
B)0.05
C)0.2743
D)0.5485

Question 71

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.5270 \\\text { R Square } & 0.2778 \\\text { Adjusted R Square } & 0.1928 \\\text { Standard Error } & 40.9107 \\\text { Observations } & 20 \\\hline\end{array}\\\text { ANOVA }\end{array}$$

$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\\text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\\text { Total } & 19 & 39395.6218 & &\\\hline \end{array}$
13-22 Multiple Regression $$\begin{array}{l}\begin{array} { l r r r r r r } \hline & \text { Coefficients } & { \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\\text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\\text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\\hline\end{array}\\\text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672\end{array}$$

-Referring to SCENARIO 13-6, what can we say about the regression model?

A)The model explains 17.12% of the variability of heating costs; after correcting for the degrees of freedom, the model explains 27.78% of the sample variability of heating costs.
B)The model explains 19.28% of the variability of heating costs; after correcting for the degrees of freedom, the model explains 27.78% of the sample variability of heating costs.
C)The model explains 27.78% of the variability of heating costs; after correcting for the degrees of freedom, the model explains 19.28% of the sample variability of heating costs.
D)The model explains 19.28% of the variability of heating costs; after correcting for the degrees of freedom, the model explains 17.12% of the sample variability of heating costs.

Question 72

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what is the p-value for testing whether Capital has a negative influence on corporate sales?

A)0.05
B)0.2743
C)0.5485
D)0.7258

Question 73

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, one company in the sample had sales of $20 billion (Sales =20,000).This company spent $300 million on capital and $700 million on wages.What is the residual (in millions of dollars) for this data point?

A)874.55
B)622.87
C)-790.69
D)-983.56

Question 74

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what is the p-value for Capital?

A)0.01
B)0.025
C)0.05
D)None of the above

Question 75

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, what are the predicted sales (in millions of dollars) for a company spending $500 million on capital and $200 million on wages?

A)15,800.00
B)16,520.07
C)17,277.49
D)20,455.98

Question 76

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, the observed value of the F-statistic is given on the printout as25.432.What are the degrees of freedom for this F-statistic?

A)25 for the numerator, 2 for the denominator
B)2 for the numerator, 23 for the denominator
C)23 for the numerator, 25 for the denominator
D)2 for the numerator, 25 for the denominator

Question 77

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.5270 \\\text { R Square } & 0.2778 \\\text { Adjusted R Square } & 0.1928 \\\text { Standard Error } & 40.9107 \\\text { Observations } & 20 \\\hline\end{array}\\\text { ANOVA }\end{array}$$

$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\\text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\\text { Total } & 19 & 39395.6218 & &\\\hline \end{array}$
13-22 Multiple Regression $$\begin{array}{l}\begin{array} { l r r r r r r } \hline & \text { Coefficients } & { \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\\text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\\text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\\hline\end{array}\\\text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672\end{array}$$

-Referring to SCENARIO 13-6, what is your decision and conclusion for the testH0 : $\beta$ 2 = 0 vs.H1 : $\beta$ 2 $\neq$ 0 at the $\alpha$ = 0.01 level of significance?

A)Do not reject H0 and conclude that the amount of insulation has a linear effect on heating costs.
B)Reject H0 and conclude that the amount of insulation does not have a linear effect on heating costs.
C)Reject H0 and conclude that the amount of insulation has a linear effect on heating costs.
D)Do not reject H0 and conclude that the amount of insulation does not have a linear effect on heating costs.

Question 78

SCENARIO 13-5
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.The Microsoft Excel output below shows results of this multiple regression. SUMMARY OUTPUT
Regression Statistics
$\begin{array} { l l } \text { Multiple R } & 0.830 \\ \text { R Square } & 0.689 \\ \text { Adjusted R Square } & 0.662 \\ \text { Standard Error } & 17501.643 \\ \text { Observations } & 26 \end{array}$
ANOVA
$\begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 15579777040 & 7789888520 & 25.432 & 0.0001 \\ \text { Residual } & 23 & 7045072780 & 306307512 & & \\ \text { Total } & 25 & 22624849820 & & & \end{array}$

$\begin{array}{lrrrc} & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\\text { Intercept } & 15800.0000 & 6038.2999 & 2.617 & 0.0154 \\\text { Capital } & 0.1245 & 0.2045 & 0.609 & 0.5485 \\\text { Wages } & 7.0762 & 1.4729 & 4.804 & 0.0001\end{array}$

-Referring to SCENARIO 13-5, which of the following values for $\alpha$ is the smallest for which the regression model as a whole is significant?

A)0.00005
B)0.001
C)0.01
D)0.05

Question 79

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. 13-22 Multiple Regression
Referring to SCENARIO 13-6, the value of the partial F test statistic is forH0: Variable X2 does not significantly improve the model after variable X1 has been includedH1: Variable X2 significantly improves the model after variable X1 has been included

Question 80

SCENARIO 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. $$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.5270 \\\text { R Square } & 0.2778 \\\text { Adjusted R Square } & 0.1928 \\\text { Standard Error } & 40.9107 \\\text { Observations } & 20 \\\hline\end{array}\\\text { ANOVA }\end{array}$$

$\begin{array} { l r c c c c }\hline & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\\text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\\text { Total } & 19 & 39395.6218 & &\\\hline \end{array}$
13-22 Multiple Regression $$\begin{array}{l}\begin{array} { l r r r r r r } \hline & \text { Coefficients } & { \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\\text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\\text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\\hline\end{array}\\\text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672\end{array}$$

-Referring to SCENARIO 13-6, the estimated value of the regression parameter $\beta$ 1 in means that

A)holding the effect of the amount of insulation constant, an estimated expected $1 increase in heating costs is associated with a decrease in the daily minimum outside temperature
By 2.76 degrees.
B)holding the effect of the amount of insulation constant, a 1 degree increase in the daily minimum outside temperature results in a decrease in heating costs by $2.76.
C)holding the effect of the amount of insulation constant, a 1 degree increase in the daily minimum outside temperature results in an estimated decrease in mean heating costs by $2.76.
D)holding the effect of the amount of insulation constant, a 1% increase in the daily minimum outside temperature results in an estimated decrease in mean heating costs by 2.76%.