Deck 10: The Conic Sections
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/64
Play
Full screen (f)
Deck 10: The Conic Sections
1
Find the standard form of the equation of the following conic section.
center
A)
B)
C)
D)
center
A)
B)
C)
D)
A
2
Find the value of the unknown coordinate so that the distance between the points is as given.
and ; distance is
A)
B)
C)
D)
and ; distance is
A)
B)
C)
D)
B
3
Give the center and radius of the circle. Then sketch its graph.
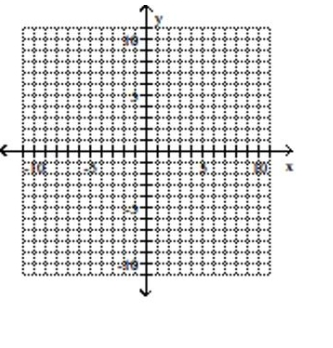 A) center
A) center
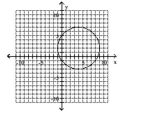
B) center
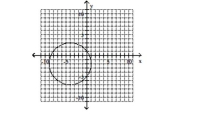
C) center
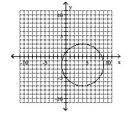
D) center
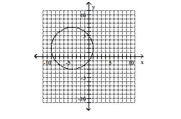
 A) center
A) center 
B) center

C) center

D) center

B
4
Find the standard form of the equation of the following conic section.
center
A)
B)
C)
D)
center
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
5
Give the center and radius of the circle. Then sketch its graph.
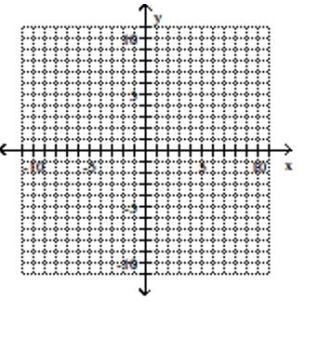 A) center
A) center
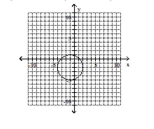
B) center
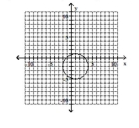
C) center
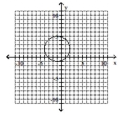
D) center
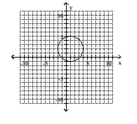
 A) center
A) center 
B) center

C) center

D) center


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
6
Find the standard form of the equation of the following conic section.
center
A)
B)
C)
D)
center
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
7
Find the distance between the pair of points. Give an exact answer.
(4, 4)and (-1, 16)
A)14 units
B)13 units
C)26 units
D)169 units
(4, 4)and (-1, 16)
A)14 units
B)13 units
C)26 units
D)169 units

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
8
Find the distance between the pair of points. Give an exact answer.
and
A) units
B) 99 units
C) 202 units
D) units
and
A) units
B) 99 units
C) 202 units
D) units

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
9
Give the center and radius of the circle. Then sketch its graph.
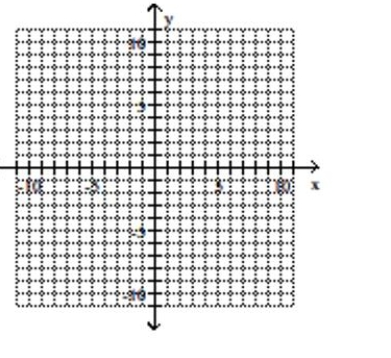
A) center

B) center
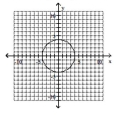
C) center

D) center

A) center

B) center

C) center

D) center


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
10
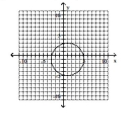
Give the center and radius of the circle. Then sketch its graph.
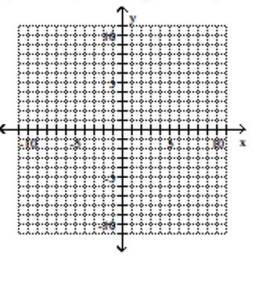 A) center B) center \(( 3,4 ) , \mathrm { r } = 4">( - 3 , - 4 ) , \mathrm { r } = 4\)<img src="https://storage.examlex.com/TB6914/11ecb33d_8774_ac61_a9b7_7d2e48059aeb_TB6914_00.jpg" alt=" Give the center and radius of the circle. Then sketch its graph. ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 16 A) center ( - 3 , - 4 ) , \mathrm { r } = 4\ ) B) center ( 3,4 ) , \mathrm { r } = 4 11 ecb33d_8d39_9252_a9b7_155027a344e9_TB6914_00 C) center ( - 3,4 ) , r = 4 D) center ( 3 , - 4 ) , r = 4 " class="answers-bank-image d-block" loading="lazy" >B) center \(( 3,4 ) , \mathrm { r } = 4 11
A) center B) center \(( 3,4 ) , \mathrm { r } = 4">( - 3 , - 4 ) , \mathrm { r } = 4\)<img src="https://storage.examlex.com/TB6914/11ecb33d_8774_ac61_a9b7_7d2e48059aeb_TB6914_00.jpg" alt=" Give the center and radius of the circle. Then sketch its graph. ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 16 A) center ( - 3 , - 4 ) , \mathrm { r } = 4\ ) B) center ( 3,4 ) , \mathrm { r } = 4 11 ecb33d_8d39_9252_a9b7_155027a344e9_TB6914_00 C) center ( - 3,4 ) , r = 4 D) center ( 3 , - 4 ) , r = 4 " class="answers-bank-image d-block" loading="lazy" >B) center \(( 3,4 ) , \mathrm { r } = 4 11
ecb33d_8d39_9252_a9b7_155027a344e9_TB6914_00
C) center
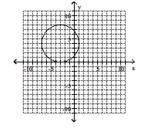
D) center
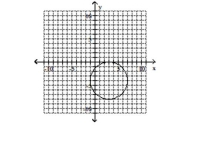
 A) center B) center \(( 3,4 ) , \mathrm { r } = 4">( - 3 , - 4 ) , \mathrm { r } = 4\)<img src="https://storage.examlex.com/TB6914/11ecb33d_8774_ac61_a9b7_7d2e48059aeb_TB6914_00.jpg" alt=" Give the center and radius of the circle. Then sketch its graph. ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 16 A) center ( - 3 , - 4 ) , \mathrm { r } = 4\ ) B) center ( 3,4 ) , \mathrm { r } = 4 11 ecb33d_8d39_9252_a9b7_155027a344e9_TB6914_00 C) center ( - 3,4 ) , r = 4 D) center ( 3 , - 4 ) , r = 4 " class="answers-bank-image d-block" loading="lazy" >B) center \(( 3,4 ) , \mathrm { r } = 4 11
A) center B) center \(( 3,4 ) , \mathrm { r } = 4">( - 3 , - 4 ) , \mathrm { r } = 4\)<img src="https://storage.examlex.com/TB6914/11ecb33d_8774_ac61_a9b7_7d2e48059aeb_TB6914_00.jpg" alt=" Give the center and radius of the circle. Then sketch its graph. ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 16 A) center ( - 3 , - 4 ) , \mathrm { r } = 4\ ) B) center ( 3,4 ) , \mathrm { r } = 4 11 ecb33d_8d39_9252_a9b7_155027a344e9_TB6914_00 C) center ( - 3,4 ) , r = 4 D) center ( 3 , - 4 ) , r = 4 " class="answers-bank-image d-block" loading="lazy" >B) center \(( 3,4 ) , \mathrm { r } = 4 11ecb33d_8d39_9252_a9b7_155027a344e9_TB6914_00
C) center

D) center


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
11
Find the distance between the pair of points. Give an exact answer.
and
A) 48 units
B) units
C) units
D) 8 units
and
A) 48 units
B) units
C) units
D) 8 units

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
12
Find the distance between the pair of points. Give an exact answer.
and
A) units
B) 2 units
C) 12 units
D) units
and
A) units
B) 2 units
C) 12 units
D) units

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
13
Find the standard form of the equation of the following conic section.
center
A)
B)
C)
D)
center
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
14
Find the value of the unknown coordinate so that the distance between the points is as given.
and ; distance is
A)
B)
C)
D)
and ; distance is
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
15
Find the value of the unknown coordinate so that the distance between the points is as given.
and ; distance is 10
A)
B)
C)
D)
and ; distance is 10
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
16
Find the distance between the pair of points. Round to the nearest thousandth.
(-4, -3.9)and (-9, 9.3)
A)18.3
B)14.115
C)199.24
D)14.077
(-4, -3.9)and (-9, 9.3)
A)18.3
B)14.115
C)199.24
D)14.077

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
17
Find the distance between the pair of points. Give an exact answer.
and
A) 45 units
B) units
C) units
D) 3 units
and
A) 45 units
B) units
C) units
D) 3 units

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
18
Find the value of the unknown coordinate so that the distance between the points is as given.
and ; distance is 13
A)
B)
C)
D)
and ; distance is 13
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
19
Find the standard form of the equation of the following conic section.
center
A)
B)
C)
D)
center
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
20
Find the distance between the pair of points. Round to the nearest thousandth.
and
A)
B) 4
C)
D)
and
A)
B) 4
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
21
Graph the parabola and label the vertex. Find the x-intercept.
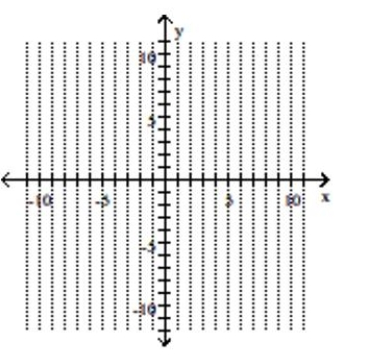 A) vertex -intercept
A) vertex -intercept
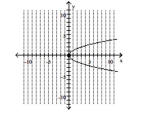
B) vertex -intercept
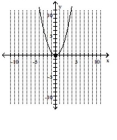
C) vertex -intercept
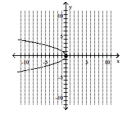
D) vertex -intercept
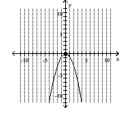
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
22
Rewrite the equation in standard form. Find the center and radius of the circle.
A)
center
B)
center
C)
center
D)
center
A)
center
B)
center
C)
center
D)
center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
23
Rewrite the equation in standard form. Find the center and radius of the circle.
A)
center
B)
center
C)
center
D)
center
A)
center
B)
center
C)
center
D)
center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
24
Give the center and radius of the circle. Then sketch its graph.
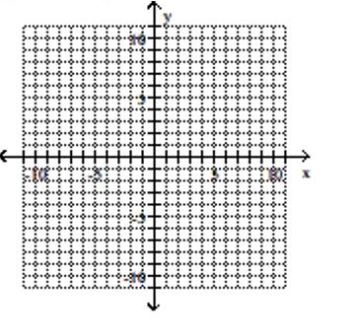 A) center
A) center
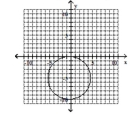
B) center
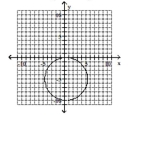
C) center
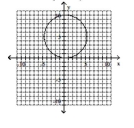
D) center
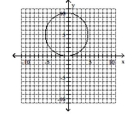
 A) center
A) center 
B) center

C) center

D) center


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
25
Use the following information to solve the problem. An airport is located at point O. A short-range radar tower is located
at point R. The maximum range at which the radar can detect a plane is 4 miles from point R.
Assume that R is 2 miles east of O and 7 miles north of O. In other words, R is located at the point (2, 7). An airplane is flying parallel to and 1 miles east of the north axis. (In other words, the plane is flying along the path
X = 1.)What is the greatest distance north of the airport at which the plane can still be detected by the radar
Tower at R? Round your answer to the nearest tenth of a mile.
A)10.9 miles
B)10 miles
C)3)1 miles
D)9)2 miles
at point R. The maximum range at which the radar can detect a plane is 4 miles from point R.
Assume that R is 2 miles east of O and 7 miles north of O. In other words, R is located at the point (2, 7). An airplane is flying parallel to and 1 miles east of the north axis. (In other words, the plane is flying along the path
X = 1.)What is the greatest distance north of the airport at which the plane can still be detected by the radar
Tower at R? Round your answer to the nearest tenth of a mile.
A)10.9 miles
B)10 miles
C)3)1 miles
D)9)2 miles

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
26
Graph the parabola and label the vertex. Find the y-intercept.
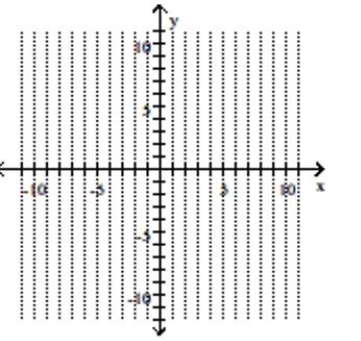 A) vertex -intercept
A) vertex -intercept
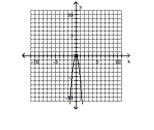
B) vertex , y-intercept
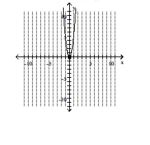
C) vertex -intercept
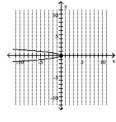
D) vertex , y-intercept
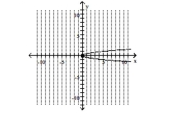
 A) vertex -intercept
A) vertex -intercept 
B) vertex , y-intercept

C) vertex -intercept

D) vertex , y-intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
27
Give the center and radius of the circle. Then sketch its graph.
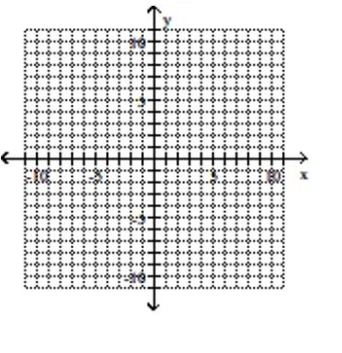 A) center
A) center
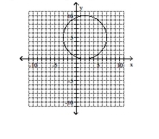
B) center
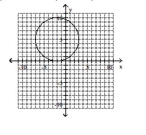
C) center
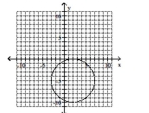
D) center
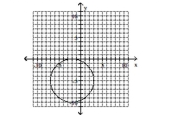
 A) center
A) center 
B) center

C) center

D) center


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
28
Graph the parabola and label the vertex. Find the x-intercept.
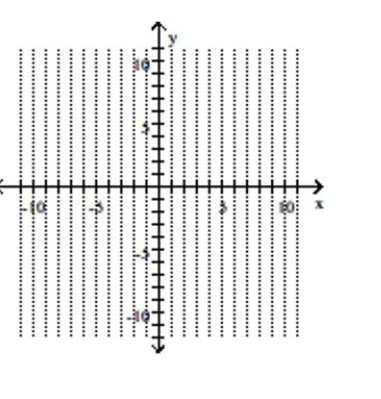 A) vertex -intercept
A) vertex -intercept
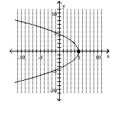
B) vertex -intercept
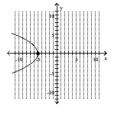
C) vertex -intercept
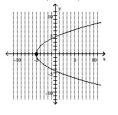
D) vertex -intercept
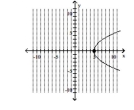
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
29
Rewrite the equation in standard form. Find the center and radius of the circle.
A)
center
B)
center
C)
center
D)
center
A)
center
B)
center
C)
center
D)
center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
30
Graph the parabola and label the vertex. Find the y-intercept.
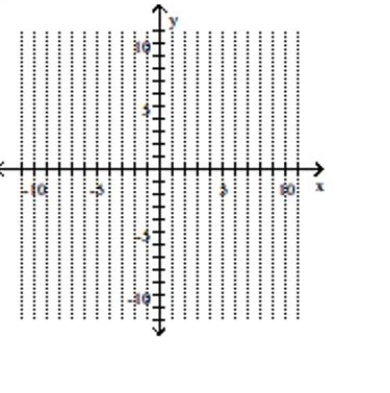 A) vertex -intercept
A) vertex -intercept
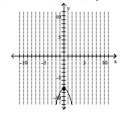
B) vertex -intercept
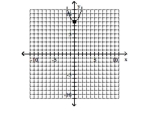
C) vertex -intercept
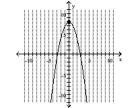
D) vertex -intercept
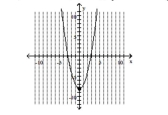
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
31
Rewrite the equation in standard form. Find the center and radius of the circle.
A)
center
B)
center
C)
center
D)
center
A)
center
B)
center
C)
center
D)
center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
32
Rewrite the equation in standard form. Find the center and radius of the circle.
A) ( x + 3 ) ^ { 2 } + ( y + 8 ) ^ { 2 } = 49 center \(( - 3 , - 8 ) , r = 49B)\(( x - 3 ) ^ { 2 } + ( y - 8 ) ^ { 2 } = 49center \(( 3,8 ) , { r } = 7C) \(( x - 8 ) ^ { 2 } + ( y - 3 ) ^ { 2 } = 49 center \(( 8,3 ) , r = 7D) \(( x - 3 ) ^ { 2 } + ( y - 8 ) ^ { 2 } = 49 center
A) ( x + 3 ) ^ { 2 } + ( y + 8 ) ^ { 2 } = 49 center \(( - 3 , - 8 ) , r = 49B)\(( x - 3 ) ^ { 2 } + ( y - 8 ) ^ { 2 } = 49center \(( 3,8 ) , { r } = 7C) \(( x - 8 ) ^ { 2 } + ( y - 3 ) ^ { 2 } = 49 center \(( 8,3 ) , r = 7D) \(( x - 3 ) ^ { 2 } + ( y - 8 ) ^ { 2 } = 49 center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
33
Rewrite the equation in standard form. Find the center and radius of the circle.
A) ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 81 center \(( - 3,4 ) , r = 9B) \(( x - 3 ) ^ { 2 } + ( y + 4 ) ^ { 2 } = 81 center \(( 3 , - 4 ) , r = 9C) \(( x - 4 ) ^ { 2 } + ( y + 3 ) ^ { 2 } = 81center \(( 4 , - 3 ) , \ { r } = 9
D) ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 81 center \(( - 3,4 ) , r = 81
A) ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 81 center \(( - 3,4 ) , r = 9B) \(( x - 3 ) ^ { 2 } + ( y + 4 ) ^ { 2 } = 81 center \(( 3 , - 4 ) , r = 9C) \(( x - 4 ) ^ { 2 } + ( y + 3 ) ^ { 2 } = 81center \(( 4 , - 3 ) , \ { r } = 9
D) ( x + 3 ) ^ { 2 } + ( y - 4 ) ^ { 2 } = 81 center \(( - 3,4 ) , r = 81

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
34
Graph the parabola and label the vertex. Find the y-intercept.
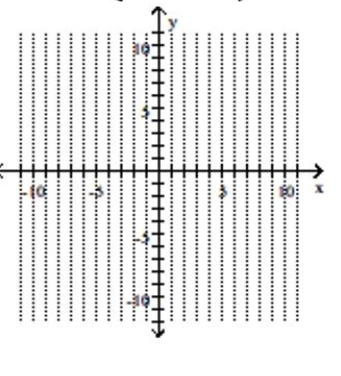 A) vertex -intercept
A) vertex -intercept
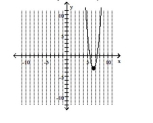
B) vertex , y-intercept
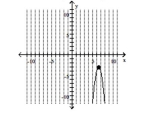
C) vertex -intercept
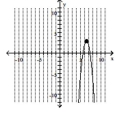
D) vertex , y-intercept
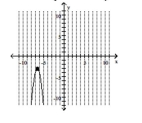
 A) vertex -intercept
A) vertex -intercept 
B) vertex , y-intercept

C) vertex -intercept

D) vertex , y-intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
35
Use the following information to solve the problem. An airport is located at point O. A short-range radar tower is located
at point R. The maximum range at which the radar can detect a plane is 4 miles from point R.
A Ferris wheel has a radius r of 25.8 feet. The height of the tower t is 49.7 feet. The distance d from the origin to the base is 43.9 feet. Find the standard form equation of the circle represented by the Ferris wheel.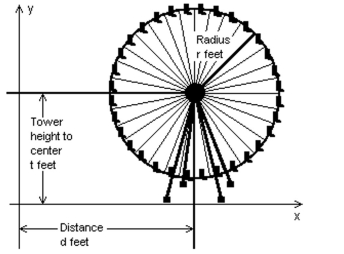
A)
B)
C)
D)
at point R. The maximum range at which the radar can detect a plane is 4 miles from point R.
A Ferris wheel has a radius r of 25.8 feet. The height of the tower t is 49.7 feet. The distance d from the origin to the base is 43.9 feet. Find the standard form equation of the circle represented by the Ferris wheel.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
36
Rewrite the equation in standard form. Find the center and radius of the circle.
A)
center
B)
center
C)
center
D)
center
A)
center
B)
center
C)
center
D)
center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
37
Graph the parabola and label the vertex. Find the y-intercept.
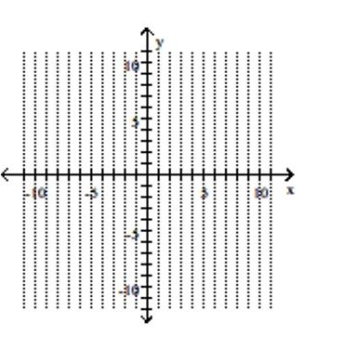 A) vertex -intercept
A) vertex -intercept
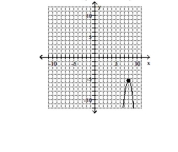
B) vertex -intercept
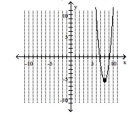
C) vertex -intercept
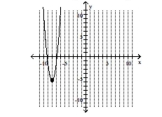
D) vertex -intercept
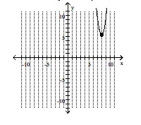
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
38
Use the following information to solve the problem. An airport is located at point O. A short-range radar tower is located
at point R. The maximum range at which the radar can detect a plane is 4 miles from point R.
Assume that R is 7 miles east of O and 11 miles north of O. In other words, R is located at the point (7, 11). An airplane is flying parallel to and 9 miles east of the north axis. (In other words, the plane is flying along the path
X = 9.)What is the shortest distance north of the airport at which the plane can still be detected by the radar
Tower at R? Round your answer to the nearest tenth of a mile.
A)24.8 miles
B)14.5 miles
C)7)5 miles
D)25.5 miles
at point R. The maximum range at which the radar can detect a plane is 4 miles from point R.
Assume that R is 7 miles east of O and 11 miles north of O. In other words, R is located at the point (7, 11). An airplane is flying parallel to and 9 miles east of the north axis. (In other words, the plane is flying along the path
X = 9.)What is the shortest distance north of the airport at which the plane can still be detected by the radar
Tower at R? Round your answer to the nearest tenth of a mile.
A)24.8 miles
B)14.5 miles
C)7)5 miles
D)25.5 miles

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
39
Rewrite the equation in standard form. Find the center and radius of the circle.
A)
center
B)
center
C)
center
D)
center
A)
center
B)
center
C)
center
D)
center

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
40
Graph the parabola and label the vertex. Find the y-intercept.
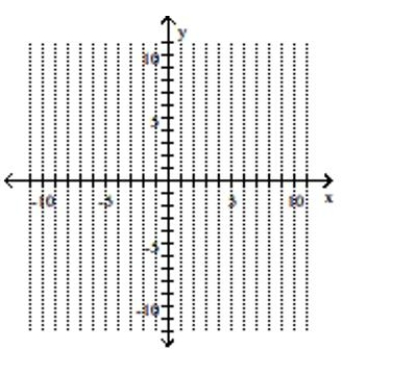 A) vertex (0, ), y-intercept
A) vertex (0, ), y-intercept

B) vertex -intercept
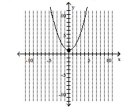
C) vertex , y-intercept
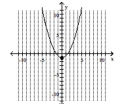
D) vertex , -intercept
1ecb33f_bda8_cb3c_a9b7_9b5b3a1737fa_TB6914_00
 A) vertex (0, ), y-intercept
A) vertex (0, ), y-intercept 
B) vertex -intercept

C) vertex , y-intercept

D) vertex , -intercept
1ecb33f_bda8_cb3c_a9b7_9b5b3a1737fa_TB6914_00

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
41
Rewrite the equation in standard form. Determine whether the parabola is horizontal or vertical, the direction it opens,
and the vertex.
A)
vertical, opens upward, vertex
B)
vertical, opens upward, vertex
C)
vertical, opens upward, vertex
D)
vertical, opens upward, vertex
and the vertex.
A)
vertical, opens upward, vertex
B)
vertical, opens upward, vertex
C)
vertical, opens upward, vertex
D)
vertical, opens upward, vertex

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
42
Rewrite the equation in standard form. Determine whether the parabola is horizontal or vertical, the direction it opens,
and the vertex.
A)
vertical, opens downward, vertex
B)
vertical, opens upward, vertex
C)
vertical, opens upward, vertex
D)
vertical, opens downward, vertex
and the vertex.
A)
vertical, opens downward, vertex
B)
vertical, opens upward, vertex
C)
vertical, opens upward, vertex
D)
vertical, opens downward, vertex

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
43
Graph the ellipse. Label the intercepts.
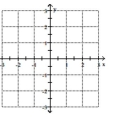
A)
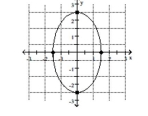
B)
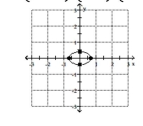
C)
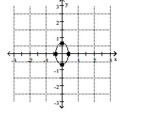
D)
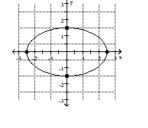

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
44
Rewrite the equation in standard form. Determine whether the parabola is horizontal or vertical, the direction it opens,
and the vertex.
A)
horizontal, opens to the right, vertex
B)
horizontal, opens to the right, vertex
C)
horizontal, opens to the left, vertex
D)
horizontal, opens to the left, vertex
and the vertex.
A)
horizontal, opens to the right, vertex
B)
horizontal, opens to the right, vertex
C)
horizontal, opens to the left, vertex
D)
horizontal, opens to the left, vertex

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
45
Graph the ellipse and label the center.
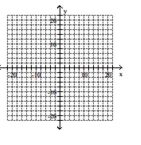
A)
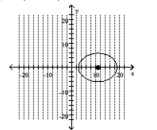
B)
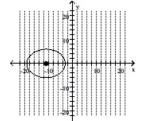
C) C
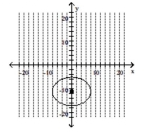
D)
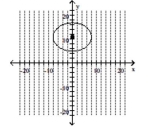

A)

B)

C) C

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
46
Graph the ellipse and label the center.
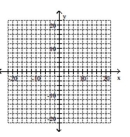
A)
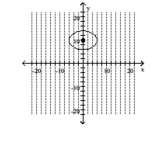
B)
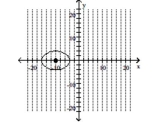
C)
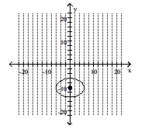
D)
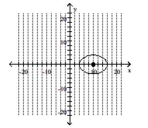

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
47
Graph the ellipse and label the center.
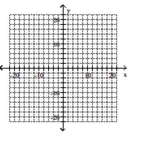
A)
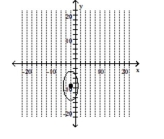
B)
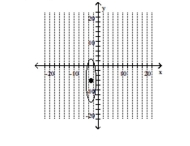
C)
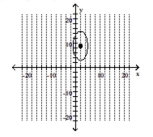
D)
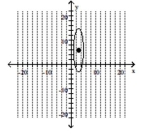

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
48
Graph the ellipse. Label the intercepts.
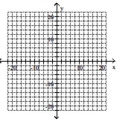
A)
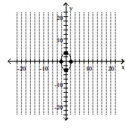
В)
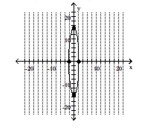
C)
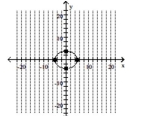
D)
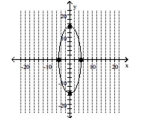

A)

В)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
49
Graph the parabola and label the vertex. Find the x-intercept.
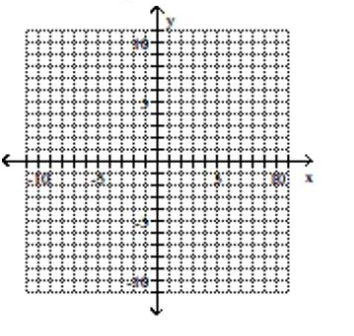 A) vertex -intercept
A) vertex -intercept
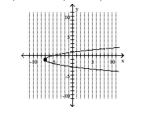
B) vertex -intercept
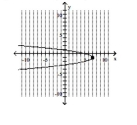
C) vertex -intercept
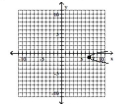
D) vertex -intercept
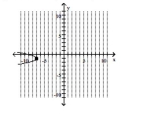
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
50
Graph the ellipse. Label the intercepts.
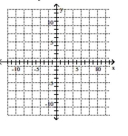
A)
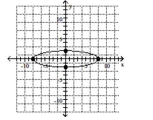
B)
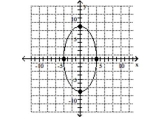
C)
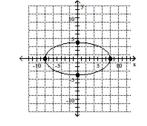
D)
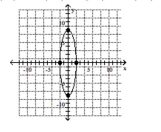

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
51
Graph the ellipse and label the center.
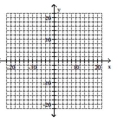
A)
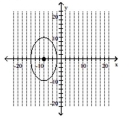
B)
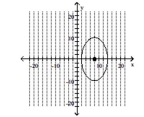
C)
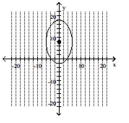
D)
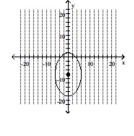

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
52
Graph the ellipse. Label the intercepts.
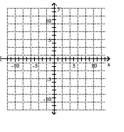
A)
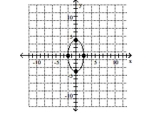
B)
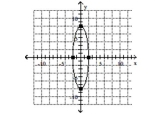
C)
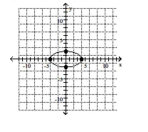
D)
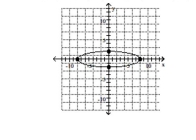

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
53
Graph the ellipse. Label the intercepts.
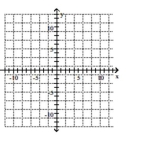
A)
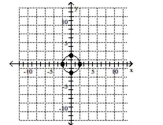
B)
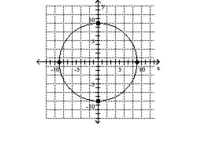
C)
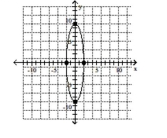
D)
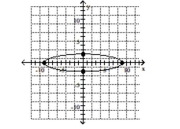

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
54
Solve.
Find an equation of the form that describes the outline of a satellite dish such that the bottom of the dish passes through , the diameter of the dish is 20 inches, and the depth of the dish is 7 inches
A)
B)
C)
D)
Find an equation of the form that describes the outline of a satellite dish such that the bottom of the dish passes through , the diameter of the dish is 20 inches, and the depth of the dish is 7 inches
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
55
Graph the ellipse. Label the intercepts.
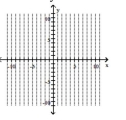
A)
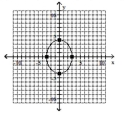
B)
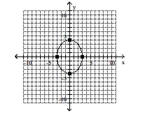
C)
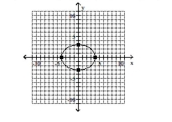
D)
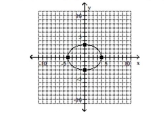

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
56
Determine the center of the ellipse.
A) (-5,-5)
B)(,5)
C) (,-5)
D) (-5,5)
A) (-5,-5)
B)(,5)
C) (,-5)
D) (-5,5)

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
57
Solve.
The effective yield from a grove of miniature pear trees is described by the equation , where is the number of pear trees per acre. What is the maximum effective yield? How many pear trees per acre should be planted to achieve the maximum yield?
A) Maximum yield
number of trees per acre planted
B) Maximum yield
number of trees per acre planted
C) Maximum yield
number of trees per acre planted
D) Maximum yield
number of trees per acre planted
The effective yield from a grove of miniature pear trees is described by the equation , where is the number of pear trees per acre. What is the maximum effective yield? How many pear trees per acre should be planted to achieve the maximum yield?
A) Maximum yield
number of trees per acre planted
B) Maximum yield
number of trees per acre planted
C) Maximum yield
number of trees per acre planted
D) Maximum yield
number of trees per acre planted

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
58
Graph the parabola and label the vertex. Find the x-intercept.
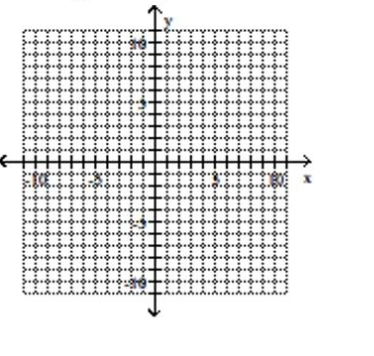 A) vertex -intercept
A) vertex -intercept
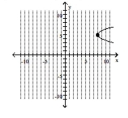
B) vertex -intercept
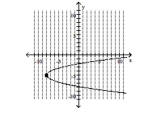
C) vertex -intercept
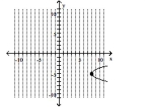
D) vertex -intercept
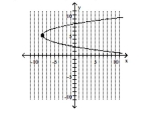
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
59
Graph the parabola and label the vertex. Find the x-intercept.
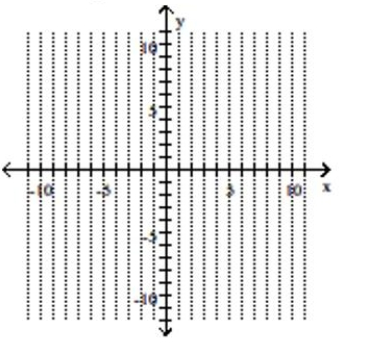 A) vertex -intercept
A) vertex -intercept
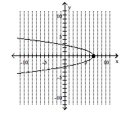
B) vertex -intercept
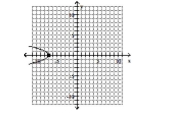
C) vertex -intercept
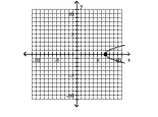
D) vertex -intercept
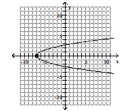
 A) vertex -intercept
A) vertex -intercept 
B) vertex -intercept

C) vertex -intercept

D) vertex -intercept


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
60
Solve.
A specialty watch company's monthly profit equation is
where is the number of watches manufactured. Find the maximum monthly profit and the number of watches must be produced each month to attain the maximum profit.
A) Maximum profit
number of watches produced
B) Maximum profit
number of watches produced
C) Maximum profit
number of watches produced
D) Maximum profit
number of watches produced
A specialty watch company's monthly profit equation is
where is the number of watches manufactured. Find the maximum monthly profit and the number of watches must be produced each month to attain the maximum profit.
A) Maximum profit
number of watches produced
B) Maximum profit
number of watches produced
C) Maximum profit
number of watches produced
D) Maximum profit
number of watches produced

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
61
Graph the ellipse and label the center.
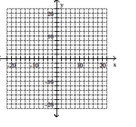
A)
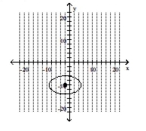
B)
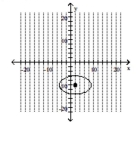
C)
D)
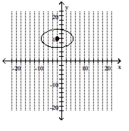

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
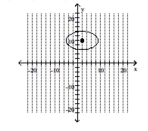
62
Graph the ellipse and label the center.
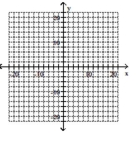
A)
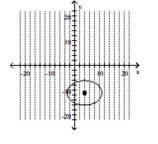
B)
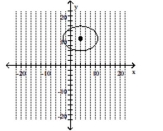
C)
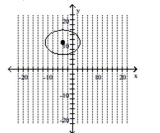
D)
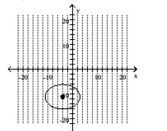

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
63
Graph the ellipse and label the center.

A)
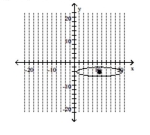
B)
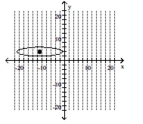
C)
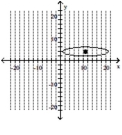
D)
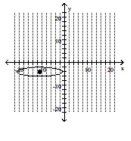

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
64
Graph the ellipse and label the center.

A)
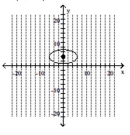
B)
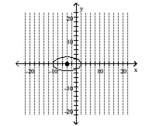
C)
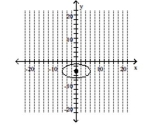
D)
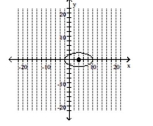

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck


