Deck 9: Quadratic Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 9: Quadratic Equations and Inequalities
1
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)
A
2
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)
C
3
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)
B
4
Solve the equation by completing the square. Express any complex numbers using i notation.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
Solve.
The formula D = 16t2 is used to approximate the distance in feet an object falls in t seconds. A package is dropped from an airplane that is 1600 feet above the ground. How many seconds elapse before it hits the
Ground?
A)10 seconds
B)25,600 seconds
C)100 seconds
D)20 seconds
The formula D = 16t2 is used to approximate the distance in feet an object falls in t seconds. A package is dropped from an airplane that is 1600 feet above the ground. How many seconds elapse before it hits the
Ground?
A)10 seconds
B)25,600 seconds
C)100 seconds
D)20 seconds

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
Solve.
The time a basketball player spends in the air is called the "hang time." The vertical leap L measured in feet is related to the hang time t measured in seconds by the equation L = 4t2. Sam Bucketmaster, a spectacular
Basketball player, often displayed a leap of 3.3 feet. Find the hang time for that leap. Round your answer to the
Nearest hundredth of a second, if necessary.
A)approximately 0.825 seconds
B)approximately 0.91 seconds
C)approximately 1.65 seconds
D)approximately 43.56 seconds
The time a basketball player spends in the air is called the "hang time." The vertical leap L measured in feet is related to the hang time t measured in seconds by the equation L = 4t2. Sam Bucketmaster, a spectacular
Basketball player, often displayed a leap of 3.3 feet. Find the hang time for that leap. Round your answer to the
Nearest hundredth of a second, if necessary.
A)approximately 0.825 seconds
B)approximately 0.91 seconds
C)approximately 1.65 seconds
D)approximately 43.56 seconds

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
Solve.
What is the value of x if the volume of the box is 729 cubic feet?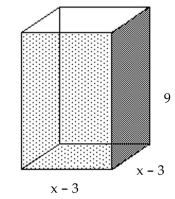
A)
B)
C)
D)
What is the value of x if the volume of the box is 729 cubic feet?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the equation by using the square root property. Express any complex numbers using i notation.
B)
C)
D)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the equation by completing the square. Express any complex numbers using i notation.



Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the equation by completing the square. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the equation by using the square root property. Express any complex numbers using i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) one rational solution
B) two rational solutions
C) two nonreal complex solutions
D) two irrational solutions
each of the following equations has. Do not solve the equation.
A) one rational solution
B) two rational solutions
C) two nonreal complex solutions
D) two irrational solutions

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two rational solutions
B) two irrational solutions
C) two nonreal complex solutions
D) one rational solution
each of the following equations has. Do not solve the equation.
A) two rational solutions
B) two irrational solutions
C) two nonreal complex solutions
D) one rational solution

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two irrational solutions
B) one rational solution
C) two nonreal complex solutions
D) two rational solutions
each of the following equations has. Do not solve the equation.
A) two irrational solutions
B) one rational solution
C) two nonreal complex solutions
D) two rational solutions

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
Write a quadratic equation having the given solutions.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two irrational solutions
B) two rational solutions
C) one rational solution
D) two nonreal complex solutions
each of the following equations has. Do not solve the equation.
A) two irrational solutions
B) two rational solutions
C) one rational solution
D) two nonreal complex solutions

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two nonreal complex solutions
B) two rational solutions
C) two irrational solutions
D) one rational solution
each of the following equations has. Do not solve the equation.
A) two nonreal complex solutions
B) two rational solutions
C) two irrational solutions
D) one rational solution

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
Write a quadratic equation having the given solutions.
9,10
A)
B)
C)
D)
9,10
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two nonreal complex solutions
B) one rational solution
C) two rational solutions
D) two irrational solutions
each of the following equations has. Do not solve the equation.
A) two nonreal complex solutions
B) one rational solution
C) two rational solutions
D) two irrational solutions

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two nonreal complex solutions
B) one rational solution
C) two rational solutions
D) two irrational solutions
each of the following equations has. Do not solve the equation.
A) two nonreal complex solutions
B) one rational solution
C) two rational solutions
D) two irrational solutions

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
Use the discriminant to find what type of solutions (two rational, two irrational, one rational, or two nonreal complex)
each of the following equations has. Do not solve the equation.
A) two irrational solutions
B) two nonreal complex solutions
C) one rational solution
D) two rational solutions
each of the following equations has. Do not solve the equation.
A) two irrational solutions
B) two nonreal complex solutions
C) one rational solution
D) two rational solutions

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
Write a quadratic equation having the given solutions.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Solve by the quadratic formula. Simplify answers. Use i notation for nonreal complex numbers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
Make an appropriate substitution in order to obtain a quadratic equation. Find all complex values for x.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
Solve. Express any nonreal complex numbers with i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
Solve. Express any nonreal complex numbers with i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
Solve for real roots.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
Solve for real roots.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
Solve.
A company that manufactures outdoor rocking chairs makes a daily profit according to the equation , where is measured in dollars and is the number of rocking chairs made per day. Find the number of rocking chairs that must be made each day to produce a zero profit for the company. Round your answer to the nearest whole number.
A) 19 rocking chairs or 24 rocking chairs per day
B) 1914 rocking chairs or 2386 rocking chairs per day
C) 24 rocking chairs per day
D) 44 rocking chairs or 49 rocking chairs per day
A company that manufactures outdoor rocking chairs makes a daily profit according to the equation , where is measured in dollars and is the number of rocking chairs made per day. Find the number of rocking chairs that must be made each day to produce a zero profit for the company. Round your answer to the nearest whole number.
A) 19 rocking chairs or 24 rocking chairs per day
B) 1914 rocking chairs or 2386 rocking chairs per day
C) 24 rocking chairs per day
D) 44 rocking chairs or 49 rocking chairs per day

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
Write a quadratic equation having the given solutions.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
Write a quadratic equation having the given solutions.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
Make an appropriate substitution in order to obtain a quadratic equation. Find all complex values for x.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
Solve for real roots.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
Find all valid real roots for the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
Find all valid real roots for the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
Solve. Express any nonreal complex numbers with i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
Write a quadratic equation having the given solutions.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
Solve for real roots.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
Solve for real roots.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
Find all valid real roots for the equation.
A) no real roots
B)
C)
D)
A) no real roots
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
Find all valid real roots for the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
Solve for real roots.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
Solve. Express any nonreal complex numbers with i notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
Make an appropriate substitution in order to obtain a quadratic equation. Find all complex values for x.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
Solve for the specified variable. Assume that all other variables are nonzero
for
A)
B)
C)
D)
for
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
Use the Pythagorean theorem to find the missing side(s).
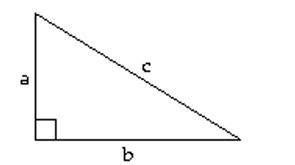
; find and
A)
B)
C)
D)

; find and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
Solve for the specified variable. Assume that all other variables are nonzero
for
A)
B)
C)
D)
for
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
Solve for the specified variable. Assume that all other variables are nonzero
A)
B)
D)
A)
B)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
Solve for the specified variable. Assume that all other variables are nonzero
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
Solve.
The area of a rectangular wall in a classroom is 105 square feet. Its length is 6 feet shorter than three times its width. Find the length and width of the wall of the classroom.
A)width = 7 ft; length = 25 ft
B)width = 7 ft; length = 27 ft
C)width = 7 ft; length = 13 ft
D)width = 7 ft; length = 15 ft
The area of a rectangular wall in a classroom is 105 square feet. Its length is 6 feet shorter than three times its width. Find the length and width of the wall of the classroom.
A)width = 7 ft; length = 25 ft
B)width = 7 ft; length = 27 ft
C)width = 7 ft; length = 13 ft
D)width = 7 ft; length = 15 ft

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
Solve for the specified variable. Assume that all other variables are nonzero
; for
A)
B)
C)
D)
; for
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
Solve for the specified variable. Assume that all other variables are nonzero
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
Solve for the specified variable. Assume that all other variables are nonzero
; for
A)
B)
C)
D)
; for
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
Solve for the specified variable. Assume that all other variables are nonzero
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
Solve.
A boat sailed a distance of 22 kilometers due south. It then banked to the left and sailed the second leg of the journey. Finally, it banked left again and sailed back to the starting point. The entire course was shaped like a
Right triangle with the 22-kilometer distance serving as the hypotenuse. The second leg of the journey was 5
Kilometers longer than the final leg. How long were the second and third legs of the journey? Round your
Answers to the nearest hundredth of a kilometer, if necessary.
A)The second leg was 18.26 kilometers. The third leg was 13.26 kilometers.
B)The second leg was 17.85 kilometers. The third leg was 12.85 kilometers.
C)The second leg was 20.35 kilometers. The third leg was 10.35 kilometers.
D)The second leg was 9.13 kilometers. The third leg was 6.63 kilometers.
A boat sailed a distance of 22 kilometers due south. It then banked to the left and sailed the second leg of the journey. Finally, it banked left again and sailed back to the starting point. The entire course was shaped like a
Right triangle with the 22-kilometer distance serving as the hypotenuse. The second leg of the journey was 5
Kilometers longer than the final leg. How long were the second and third legs of the journey? Round your
Answers to the nearest hundredth of a kilometer, if necessary.
A)The second leg was 18.26 kilometers. The third leg was 13.26 kilometers.
B)The second leg was 17.85 kilometers. The third leg was 12.85 kilometers.
C)The second leg was 20.35 kilometers. The third leg was 10.35 kilometers.
D)The second leg was 9.13 kilometers. The third leg was 6.63 kilometers.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
Solve for the specified variable. Assume that all other variables are nonzero
; for
A)
B)
C)
D)
; for
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
Use the Pythagorean theorem to find the missing side(s).

; find
A)
B) 57
C)
D)

; find
A)
B) 57
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
Make an appropriate substitution in order to obtain a quadratic equation. Find all complex values for x.
A)
B)
C) ,
D)
A)
B)
C) ,
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
Make an appropriate substitution in order to obtain a quadratic equation. Find all complex values for x.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
Solve.
A tour bus is traveling along a triangular path. The three straight lines form a right triangle. One leg of the triangle represents a distance of 144 miles. The other leg of the triangle is 96 miles shorter than the hypotenuse.
What is the length of the hypotenuse of this triangle? Of the other leg?
A)The hypotenuse is 159 miles long. The shorter leg is 62 miles long.
B)The hypotenuse is 155 miles long. The shorter leg is 58 miles long.
C)The hypotenuse is 156 miles long. The shorter leg is 60 miles long.
D)The hypotenuse is 158 miles long. The shorter leg is 59 miles long.
A tour bus is traveling along a triangular path. The three straight lines form a right triangle. One leg of the triangle represents a distance of 144 miles. The other leg of the triangle is 96 miles shorter than the hypotenuse.
What is the length of the hypotenuse of this triangle? Of the other leg?
A)The hypotenuse is 159 miles long. The shorter leg is 62 miles long.
B)The hypotenuse is 155 miles long. The shorter leg is 58 miles long.
C)The hypotenuse is 156 miles long. The shorter leg is 60 miles long.
D)The hypotenuse is 158 miles long. The shorter leg is 59 miles long.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
Solve. Find all valid real roots for the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
Solve for the specified variable. Assume that all other variables are nonzero
; for
A)
B)
C)
D)
; for
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
Solve.
The area of a triangular poster is 1480 square centimeters. Its altitude is 6 feet shorter than twice its base. Find the lengths of the altitude and base.
A)base = 40 cm; altitude = 37 cm
B)base = 20 cm; altitude = 74 cm
C)base = 40 cm; altitude = 74 cm
D)base = 80 cm; altitude = 18.5 cm
The area of a triangular poster is 1480 square centimeters. Its altitude is 6 feet shorter than twice its base. Find the lengths of the altitude and base.
A)base = 40 cm; altitude = 37 cm
B)base = 20 cm; altitude = 74 cm
C)base = 40 cm; altitude = 74 cm
D)base = 80 cm; altitude = 18.5 cm

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


