Deck 6: Normal Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/60
Play
Full screen (f)
Deck 6: Normal Probability Distributions
1
Find the probability that in 200 tosses of a fair die, we will obtain at most 30 fives. Use the normal distribution to approximate the desired probability.
A) 0.1871
B) 0.2946
C) 0.4936
D) 0.3229
A) 0.1871
B) 0.2946
C) 0.4936
D) 0.3229
B
2
For women aged 18-24, systolic blood pressures are normally distributed with a mean of 114.8 mm Hg and a standard deviation of 13.1 mm Hg. If 23 women aged 18-24 are randomly selected, find the probability that their mean systolic blood pressure is between 119 and 122 mm Hg.
A) 0.9341
B) 0.3343
C) 0.0577
D) 0.0833
A) 0.9341
B) 0.3343
C) 0.0577
D) 0.0833
0.0577
3
Estimate the probability of getting exactly 43 boys in 90 births. Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution.
A) 0.0764
B) 0.0729
C) 0.0159
D) 0.1628
A) 0.0764
B) 0.0729
C) 0.0159
D) 0.1628
A
4
The lengths of human pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. What is the probability that a pregnancy last at least 300 days?
A) 0.0166
B) 0.4834
C) 0.0179
D) 0.9834
A) 0.0166
B) 0.4834
C) 0.0179
D) 0.9834

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
5
The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability. The probability of exactly 44 green marbles
A) The area between 43.5 and 45.5
B) The area between 43.5 and 44
C) The area between 43.5 and 44.5
D) The area between 44 and 44.5
A) The area between 43.5 and 45.5
B) The area between 43.5 and 44
C) The area between 43.5 and 44.5
D) The area between 44 and 44.5

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
6
The continuity correction is used to compensate for the fact that a ___________distribution is used to approximate a ____________ distribution.
A) discrete; continuous
B) continuous; discrete
C) discrete; uniform
D) binomial; uniform
A) discrete; continuous
B) continuous; discrete
C) discrete; uniform
D) binomial; uniform

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
7
Find the area of the shaded region. The graph depicts the standard normal distribution with mean 0 and standard deviation 1. 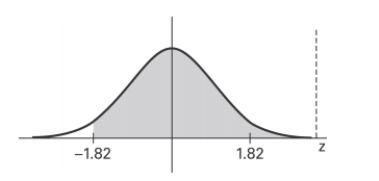
A) 0.4656
B) 0.9656
C) 0.0344
D) −0.0344

A) 0.4656
B) 0.9656
C) 0.0344
D) −0.0344

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
8
The distribution of certain test scores is a nonstandard normal distribution with a mean of 50 and a standard deviation of 6. What are the values of the mean and standard deviation after all test scores have been standardized by converting them to z-scores using zx=−()μ /σ?
A) The mean is 100 and the standard deviation is 10.
B) The mean is 0 and the standard deviation is 1.
C) The mean is 10 and the standard deviation is 100.
D) The mean is 1 and the standard deviation is 0.
A) The mean is 100 and the standard deviation is 10.
B) The mean is 0 and the standard deviation is 1.
C) The mean is 10 and the standard deviation is 100.
D) The mean is 1 and the standard deviation is 0.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
9
Assume that the weight loss for the first month of a diet program varies between 6 pounds and 12 pounds, and is spread evenly over the range of possibilities, so that there is a uniform distribution. Find the probability that the given range of pounds lost is between 8 pounds and 11 pounds.
A)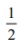
B)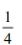
C)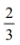
D)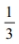
A)
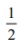
B)
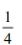
C)
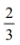
D)
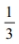

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
10
For the binomial distribution with n=24 and p=0.6 , state whether or not it is suitable to use the normal distribution as an approximation.
A) Normal approximation is suitable.
B) Normal approximation is not suitable.
A) Normal approximation is suitable.
B) Normal approximation is not suitable.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
11
Using the following uniform density curve, answer the question.
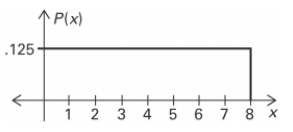
What is the probability that the random variable has a value greater than 5 ?
A) 0.325
B) 0.250
C) 0.375
D) 0.500

What is the probability that the random variable has a value greater than 5 ?
A) 0.325
B) 0.250
C) 0.375
D) 0.500

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
12
If a histogram of a sample of men's ages is skewed, what do you expect to see in the normal quantile plot?
A) Points are following a straight-line pattern.
B) Points are not following a straight-line pattern.
A) Points are following a straight-line pattern.
B) Points are not following a straight-line pattern.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
13
A bank's loan officer rates applicants for credit. The ratings are normally distributed with a mean of 200 and a standard deviation of 50 . Find 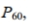 the score which separates the lower 60% from the top 40% .
the score which separates the lower 60% from the top 40% .
A) 187.5
B) 212.5
C) 207.8
D) 211.3
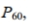 the score which separates the lower 60% from the top 40% .
the score which separates the lower 60% from the top 40% .A) 187.5
B) 212.5
C) 207.8
D) 211.3

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
14
Assume that z scores are normally distributed with a mean of 0 and a standard deviation of 1. If 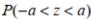 =0.4314 , find
=0.4314 , find 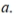
A) -0.18
B) 0.3328
C) 0.57
D) 1.49
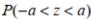 =0.4314 , find
=0.4314 , find 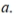
A) -0.18
B) 0.3328
C) 0.57
D) 1.49

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
15
If z is a standard normal variable, find the probability that z lies between −2.41 and 0
A) 0.5080
B) 0.4910
C) 0.0948
D) 0.4920
A) 0.5080
B) 0.4910
C) 0.0948
D) 0.4920

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
16
Scores on a test have a mean of 70 and 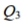 is 83 . The scores have a distribution that is approximately normal. Find
is 83 . The scores have a distribution that is approximately normal. Find 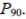 (You will need to first find the standard deviation.)
(You will need to first find the standard deviation.)
A) 92.9
B) 93.7
C) 95.6
D) 94.8
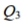 is 83 . The scores have a distribution that is approximately normal. Find
is 83 . The scores have a distribution that is approximately normal. Find 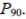 (You will need to first find the standard deviation.)
(You will need to first find the standard deviation.)A) 92.9
B) 93.7
C) 95.6
D) 94.8

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
17
A study of the amount of time it takes a mechanic to rebuild the transmission for a 2010 Chevrolet Colorado shows that the mean is 8.4 hours and the standard deviation is 1.8 hours. If 40 mechanics are randomly selected, find the probability that their mean rebuild time is less
Than 8.9 hours.
A) 0.9589
B) 0.4276
C) 0.9608
D) 0.9756
Than 8.9 hours.
A) 0.9589
B) 0.4276
C) 0.9608
D) 0.9756

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
18
If a sample size is < _____, the sample size must come from a population having a normal distribution in order to follow normal distribution calculations.
A) 30
B) 40
C) 50
D) 100
A) 30
B) 40
C) 50
D) 100

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
19
Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution. Estimate P(6) for n=18 and p=0.3 .
A) 0.1239
B) 0.1015
C) 0.8513
D) 0.1958
A) 0.1239
B) 0.1015
C) 0.8513
D) 0.1958

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
20
The heights of adult females are normally distributed. If you were to construct a histogram of 40 randomly selected women, what shape would the histogram of those heights have and what pattern would you expect in a normal quantile plot of these data?
A) The histogram would be approximately bell-shaped, and the normal quantile plot would have data points have follow a straight-line pattern.
B) The histogram would by approximately bell-shaped, and the normal quantile plot would have data points that would be bell-shaped.
C) The histogram would by non-symmetric, and the normal quantile plot would have data points that would be non-linear.
D) The histogram would by approximately bell-shaped, and the normal quantile plot would have data points that would be non-linear.
A) The histogram would be approximately bell-shaped, and the normal quantile plot would have data points have follow a straight-line pattern.
B) The histogram would by approximately bell-shaped, and the normal quantile plot would have data points that would be bell-shaped.
C) The histogram would by non-symmetric, and the normal quantile plot would have data points that would be non-linear.
D) The histogram would by approximately bell-shaped, and the normal quantile plot would have data points that would be non-linear.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
21
A baseball player has a batting average of 0.346, so the probability of a hit is 0.346. Assume that his hitting attempts are independent of each other. Assume that the batter gets up to bat 4 times in each game. Estimate the probability that in 50 consecutive games, there are at least
45 games in which the batter gets at least one hit. (Hint: first find the probability that in one
Game the batter gets at least one hit)
A) 0.0918
B) 0.0446
C) 0.0643
D) 0.8171
45 games in which the batter gets at least one hit. (Hint: first find the probability that in one
Game the batter gets at least one hit)
A) 0.0918
B) 0.0446
C) 0.0643
D) 0.8171

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
22
The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability. The probability of no more than 35 defective CDs
A) The area to the left of 35
B) The area to the left of 35.5
C) The area to the right of 35.5
D) The area to the left of 34.5
A) The area to the left of 35
B) The area to the left of 35.5
C) The area to the right of 35.5
D) The area to the left of 34.5

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
23
A coin is tossed 20 times. A person who claims to have extrasensory perception is asked to predict the outcome of each flip in advance. She predicts correctly on 14 tosses. What is the probability of being correct 14 or more times by guessing? Does this probability seem to
Verify her claim? Use the normal distribution to approximate the desired probability.
A) 0.4418, no
B) 0.4418, yes
C) 0.0582, no
D) 0.0582, yes
Verify her claim? Use the normal distribution to approximate the desired probability.
A) 0.4418, no
B) 0.4418, yes
C) 0.0582, no
D) 0.0582, yes

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
24
Scores on a test are normally distributed with a mean of 63.2 and a standard deviation of 11.7 . Find 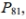 which separates the bottom 81 % from the top 19% .
which separates the bottom 81 % from the top 19% .
A) 0.291
B) 73.5
C) 0.88
D) 66.6
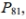 which separates the bottom 81 % from the top 19% .
which separates the bottom 81 % from the top 19% .A) 0.291
B) 73.5
C) 0.88
D) 66.6

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
25
The probability that a radish seed will germinate is 0.7. Estimate the probability that of 140 randomly selected seeds, exactly 100 will germinate.
A) 0.0679
B) 0.9331
C) 0.0669
D) 0.0769
A) 0.0679
B) 0.9331
C) 0.0669
D) 0.0769

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
26
In one region, the September energy consumption levels for single -family homes are found to be normally distributed with a mean of 1050 kWh and a standard deviation of 218 kWh. For a randomly selected home, find the probability that the September energy consumption level is
Between 1100 kWh and 1225 kWh.
A) 0.3791
B) 0.2881
C) 0.1971
D) 0.0910
Between 1100 kWh and 1225 kWh.
A) 0.3791
B) 0.2881
C) 0.1971
D) 0.0910

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
27
Assume that the red blood cell counts of women are normally distributed with a mean of 4.577 million cells per microliter and a standard deviation of 0.382 million cells per microliter. Find the value closest to the probability that a randomly selected woman has a red
Blood cell count above the normal range of 4.2 to 5.4 million cells per microliter.
A) 0.1611
B) 0.0409
C) 0.0158
D) 0.9842
Blood cell count above the normal range of 4.2 to 5.4 million cells per microliter.
A) 0.1611
B) 0.0409
C) 0.0158
D) 0.9842

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
28
Assume that the red blood cell counts of women are normally distributed with a mean of 4.577 million cells per microliter and a standard deviation of 0.382 million cells per microliter. Find the 80th percentile for the red blood cell counts of women.
A) 4.655 million cells per microliter
B) 4.898 million cells per microliter
C) 4.565 million cells per microliter
D) 4.878 million cells per microliter
A) 4.655 million cells per microliter
B) 4.898 million cells per microliter
C) 4.565 million cells per microliter
D) 4.878 million cells per microliter

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
29
The weights of college football players are normally distributed with a mean of 200 pounds and a standard deviation of 50 pounds. If a college football player is randomly selected, find the probability that he weighs between 170 and 220 pounds.
A) 0.1554
B) 0.3811
C) 0.2257
D) 0.0703
A) 0.1554
B) 0.3811
C) 0.2257
D) 0.0703

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
30
Which of the following is a biased estimator?
A) proportion
B) variance
C) mean
D) standard deviation
A) proportion
B) variance
C) mean
D) standard deviation

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
31
An unbiased estimator is a statistic that targets the value of the of the population parameter such that the sampling distribution of the statistic has a __________equal to the _________ of the corresponding parameter.
A) mean; mean
B) standard deviation; standard deviation
C) mean; standard deviation
D) range; range/4
A) mean; mean
B) standard deviation; standard deviation
C) mean; standard deviation
D) range; range/4

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
32
Assume that the red blood cell counts of women are normally distributed with a mean of 4.577 million cells per microliter and a standard deviation of 0.382 million cells per microliter. Approximately what percentage of women have red blood cell counts in the
Normal range from 4.2 to 5.4 million cells per microliter?
A) 82.31%
B) 17.69%
C) 4.09%
D) 16.11%
Normal range from 4.2 to 5.4 million cells per microliter?
A) 82.31%
B) 17.69%
C) 4.09%
D) 16.11%

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
33
Estimate the indicated probability by using the normal distribution as an approximation to the binomial distribution. Two percent of hair dryers produced in a certain plant are defective. Estimate the probability that of 10,000 randomly selected hair dryers, at least 219
Are defective.
A) 0.0823
B) 0.9066
C) 0.0869
D) 0.0934
Are defective.
A) 0.0823
B) 0.9066
C) 0.0869
D) 0.0934

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
34
Find the area of the shaded region. The graph depicts the standard normal distribution with mean 0 and standard deviation 1. 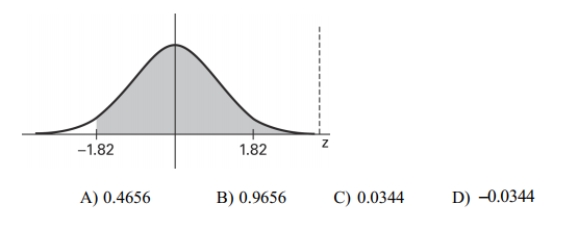


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
35
The Precision Scientific Instrument Company manufactures thermometers that are supposed to give readings of 0°C at the freezing point of water. Tests on a large sample of these thermometers reveal that at the freezing point of water, some give readings below 0°C
(denoted by negative numbers)and some give readings above 0°C (denoted by positive
Numbers). Assume that the mean reading is 0°C and the standard deviation of the readings is
1)00°C. Also assume that the frequency distribution of errors closely resembles the normal
Distribution. A thermometer is randomly selected and tested. A quality control analyst wants
To examine thermometers that give readings in the bottom 4%. Find the temperature reading
That separates the bottom 4% from the others.
A) −°1.75
B) −°1.63
C) −°1.48
D) −°1.89
(denoted by negative numbers)and some give readings above 0°C (denoted by positive
Numbers). Assume that the mean reading is 0°C and the standard deviation of the readings is
1)00°C. Also assume that the frequency distribution of errors closely resembles the normal
Distribution. A thermometer is randomly selected and tested. A quality control analyst wants
To examine thermometers that give readings in the bottom 4%. Find the temperature reading
That separates the bottom 4% from the others.
A) −°1.75
B) −°1.63
C) −°1.48
D) −°1.89

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
36
A bank's loan officer rates applicants for credit. The ratings are normally distributed with a mean of 200 and a standard deviation of 50. If an applicant is randomly selected, find the probability of a rating that is between 200 and 275.
A) 0.4332
B) 0.9332
C) 0.0668
D) 0.5
A) 0.4332
B) 0.9332
C) 0.0668
D) 0.5

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
37
Find the indicated z score. The graph depicts the standard normal distribution with mean 0 and standard deviation 1. Shaded area is 0.4483. 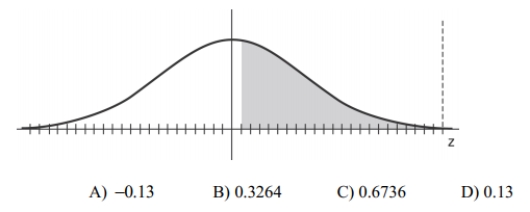


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
38
If z is a standard normal variable, find the probability: 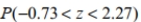
A) 0.7557
B) 1.54
C) 0.4884
D) 0.2211
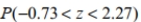
A) 0.7557
B) 1.54
C) 0.4884
D) 0.2211

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
39
If z is a standard normal variable, find 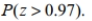
A) 0.1922
B) 0.1660
C) 0.8340
D) 0.1685
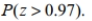
A) 0.1922
B) 0.1660
C) 0.8340
D) 0.1685

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
40
In a population of 210 women, the heights of the women are normally distributed with a mean of 64.4 inches and a standard deviation of 2.9 inches. If 36 women are selected at random, find the mean 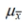 and standard deviation
and standard deviation 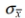 of the population of sample means. Assume that the sampling is done without replacement and use a finite population correction factor.
of the population of sample means. Assume that the sampling is done without replacement and use a finite population correction factor.
A) 64.4 inches, 2.07 inches
B) 58.8 inches, 2.65 inches
C) 64.4 inches, 2.9 inches
D) 64.4 inches, 0.44 inches
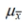 and standard deviation
and standard deviation 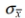 of the population of sample means. Assume that the sampling is done without replacement and use a finite population correction factor.
of the population of sample means. Assume that the sampling is done without replacement and use a finite population correction factor.A) 64.4 inches, 2.07 inches
B) 58.8 inches, 2.65 inches
C) 64.4 inches, 2.9 inches
D) 64.4 inches, 0.44 inches

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
41
Three randomly selected households are surveyed as a pilot project for a larger survey to be conducted later. The numbers of people in the households are 2, 3, and 8. Consider the
values of 2, 3, and 8 to be a population. Assume that samples of size n = 2 are randomly
selected with replacement from the population of 2, 3, and 8. The nine different samples are
as follows:
(2, 2), (2, 3), (2, 8), (3, 2), (3, 3), (3, 8), (8, 2), (8, 3), and (8, 8).
(i)Find the range of each of the nine samples, then summarize the sampling distribution of the
ranges in the format of a table representing the probability distribution. (ii)Compare the
population range to the mean of the sample ranges. (iii)Do the sample ranges target the value
of the population range? In general, do ranges make good estimators of population ranges?
Why or why not?
values of 2, 3, and 8 to be a population. Assume that samples of size n = 2 are randomly
selected with replacement from the population of 2, 3, and 8. The nine different samples are
as follows:
(2, 2), (2, 3), (2, 8), (3, 2), (3, 3), (3, 8), (8, 2), (8, 3), and (8, 8).
(i)Find the range of each of the nine samples, then summarize the sampling distribution of the
ranges in the format of a table representing the probability distribution. (ii)Compare the
population range to the mean of the sample ranges. (iii)Do the sample ranges target the value
of the population range? In general, do ranges make good estimators of population ranges?
Why or why not?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
42
The number of books sold over the course of the four-day book fair were 194, 197, 247, and 76. Assume that samples of size 2 are randomly selected with replacement from this
population of four values. List the different possible samples, and find the mean of each of
them.
population of four values. List the different possible samples, and find the mean of each of
them.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
43
A normal quartile plot is given below for a sample of scores on an aptitude test. Use the plot to assess the normality of scores on this test. Explain your reasoning. 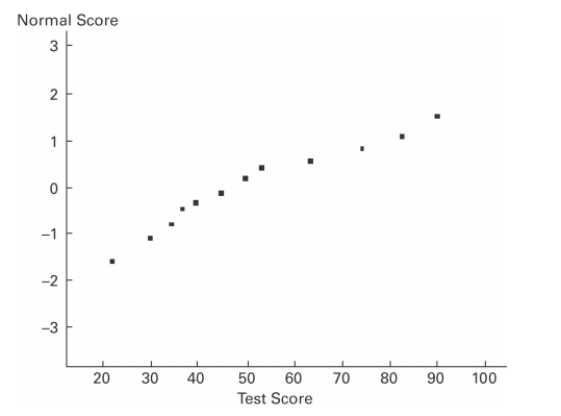


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
44
After constructing a new manufacturing machine, five prototype integrated circuit chips are produced and it is found that two are defective and three are acceptable. Assume that two of
the chips are randomly selected with replacement from this population. After identifying the
25 possible samples, find the proportion of defects in each of them, using a table to describe
the sampling distribution of the proportions of the defects.
the chips are randomly selected with replacement from this population. After identifying the
25 possible samples, find the proportion of defects in each of them, using a table to describe
the sampling distribution of the proportions of the defects.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
45
Define a density curve and describe the two properties that it must satisfy. Show a density curve for a uniform distribution. Make sure that your graph satisfies both properties.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
46
A normal quartile plot is given below for the lifetimes (in hours)of a sample of batteries of a particular brand. Use the plot to assess the normality of the lifetimes of these batteries.
Explain your reasoning.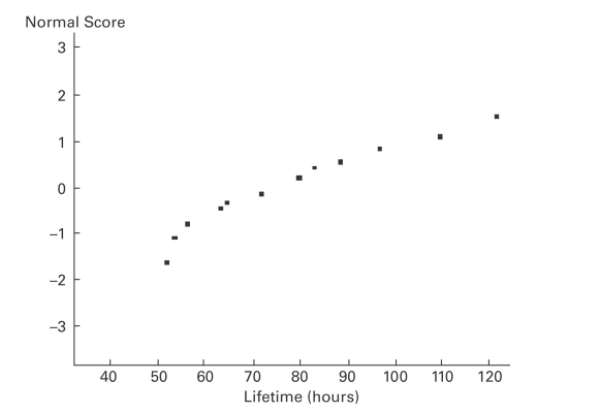
Explain your reasoning.


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
47
The population of current statistics students has ages with mean 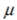 and standard deviation
and standard deviation 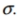 Samples of statistics are randomly selected so that there are exactly 40 students in each sample. For each sample, the mean age is computed. What does the central limit theorem tell us about the distribution of those mean ages?
Samples of statistics are randomly selected so that there are exactly 40 students in each sample. For each sample, the mean age is computed. What does the central limit theorem tell us about the distribution of those mean ages?
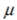 and standard deviation
and standard deviation 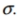 Samples of statistics are randomly selected so that there are exactly 40 students in each sample. For each sample, the mean age is computed. What does the central limit theorem tell us about the distribution of those mean ages?
Samples of statistics are randomly selected so that there are exactly 40 students in each sample. For each sample, the mean age is computed. What does the central limit theorem tell us about the distribution of those mean ages?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
48
Three randomly selected households are surveyed as a pilot project for a larger survey to be conducted later. The numbers of people in the households are 5, 7, and 9. Consider the
values of 5, 7, and 9 to be a population. Assume that samples of size n = 2 are randomly
selected with replacement from the population of 5, 7, and 9. The nine different samples are
as follows: (5, 5), (5, 7), (5, 9), (7, 5), (7, 7), (7, 9), (9, 5), (9, 7), and (9, 9). (i)Find the mean
of each of the nine samples, then summarize the sampling distribution of the means in the
format of a table representing the probability distribution. (ii)Compare the population mean
to the mean of the sample means. (iii)Do the sample means target the value of the
population mean? In general, do means make good estimators of population means? Why or
why not?
values of 5, 7, and 9 to be a population. Assume that samples of size n = 2 are randomly
selected with replacement from the population of 5, 7, and 9. The nine different samples are
as follows: (5, 5), (5, 7), (5, 9), (7, 5), (7, 7), (7, 9), (9, 5), (9, 7), and (9, 9). (i)Find the mean
of each of the nine samples, then summarize the sampling distribution of the means in the
format of a table representing the probability distribution. (ii)Compare the population mean
to the mean of the sample means. (iii)Do the sample means target the value of the
population mean? In general, do means make good estimators of population means? Why or
why not?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
49
You will use a normal distribution to approximate a binomial distribution. Complete the following table for a distribution in which 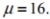
It might be helpful to make a diagram to help you determine the continuity factor for each entry.

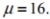
It might be helpful to make a diagram to help you determine the continuity factor for each entry.


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose that you wish to find 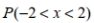 for a continuous uniform distribution having a minimum of -3 and a maximum of 3 . If you incorrectly assume that the distribution is normal instead of uniform, will your answer be too big, too small, or will you still obtain the correct answer? Explain your thinking.
for a continuous uniform distribution having a minimum of -3 and a maximum of 3 . If you incorrectly assume that the distribution is normal instead of uniform, will your answer be too big, too small, or will you still obtain the correct answer? Explain your thinking.
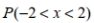 for a continuous uniform distribution having a minimum of -3 and a maximum of 3 . If you incorrectly assume that the distribution is normal instead of uniform, will your answer be too big, too small, or will you still obtain the correct answer? Explain your thinking.
for a continuous uniform distribution having a minimum of -3 and a maximum of 3 . If you incorrectly assume that the distribution is normal instead of uniform, will your answer be too big, too small, or will you still obtain the correct answer? Explain your thinking.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
51
Describe what an unbiased estimator is and give an example of an unbiased estimator and a biased estimator.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
52
SAT verbal scores are normally distributed with a mean of 430 and a standard deviation of 120 (based on data from the College Board ATP). (a)If a single student is randomly selected,
find the probability that the sample mean is above 500. (b)If a sample of 35 students are
selected randomly, find the probability that the sample mean is above 500. These two
problems appear to be very similar. Which problem requires the application of the central
limit theorem, and in what way does the solution process differ between the two problems?
find the probability that the sample mean is above 500. (b)If a sample of 35 students are
selected randomly, find the probability that the sample mean is above 500. These two
problems appear to be very similar. Which problem requires the application of the central
limit theorem, and in what way does the solution process differ between the two problems?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
53
A normal quartile plot is given below for the weekly incomes (in dollars)of a sample of engineers in one town. Describe what each x value represents and what each y value
represents. Use the plot to assess the normality of the incomes of engineers in this town.
Explain your reasoning.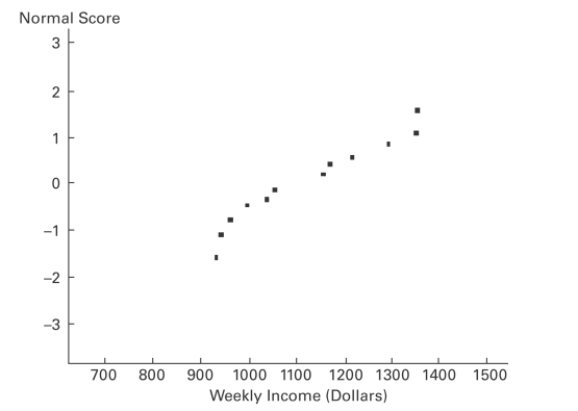
represents. Use the plot to assess the normality of the incomes of engineers in this town.
Explain your reasoning.


Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
54
In a recent year, the U.S. Mint in Denver manufactured 270 million quarters. Assume that on each day of production, a sample of 50 quarters is randomly selected and the mean weight is
obtained. Given that the population of quarters has a mean weight of 5.67 g, what do you
know about the mean of the sample means? What do you know about the shape of the
distribution of the sample means?
obtained. Given that the population of quarters has a mean weight of 5.67 g, what do you
know about the mean of the sample means? What do you know about the shape of the
distribution of the sample means?

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
55
Explain how a nonstandard normal distribution differs from the standard normal distribution. Describe the process for finding probabilities for nonstandard normal
distributions.
distributions.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
56
Identify three important criteria to determine if the use of a normal distribution is justified

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
57
State the central limit theorem. Describe the sampling distribution for a population that is uniform and for a population that is normal.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
58
Define the central limit theorem and its relationship to the sampling distribution of sample means. Define how you can approximate a normal distribution from an original population
that is not normally distributed
that is not normally distributed

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
59
Heights of adult females are normally distributed. Samples of height of adult females, each of size n=3 , are randomly collected and the sample means are found. Is it correct to conclude that the sample means cannot be treated as a normal distribution because the sample size is so small? Explain.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
60
Lengths of pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. (a)Find the probability of a pregnancy lasting more than 250 days.
(b)Find the probability of a pregnancy lasting more than 280 days. Draw the diagram for
each and discuss the part of the solution that would be different for finding the requested
probabilities.
(b)Find the probability of a pregnancy lasting more than 280 days. Draw the diagram for
each and discuss the part of the solution that would be different for finding the requested
probabilities.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck


