Deck 9: Optimization Online Only
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/55
Play
Full screen (f)
Deck 9: Optimization Online Only
1
Find all saddle points for the matrix game.


D
2
Find all saddle points for the matrix game.


A
3
Write the payoff matrix for the game.
In the traditional Japanese childrenʹs game janken (or ʺstone, scissors, paperʺ), at a given signal, each of two players shows either no fingers (stone), two fingers (scissors), or all five fingers
(paper). Stone beats scissors, scissors beats paper, and paper beats stone. In the case of a tie, there
Is no payoff. In the case of a win, the winner collects 50 yen.
In the traditional Japanese childrenʹs game janken (or ʺstone, scissors, paperʺ), at a given signal, each of two players shows either no fingers (stone), two fingers (scissors), or all five fingers
(paper). Stone beats scissors, scissors beats paper, and paper beats stone. In the case of a tie, there
Is no payoff. In the case of a win, the winner collects 50 yen.

B
4
Find all saddle points for the matrix game.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
5
Find the value of the strategy.
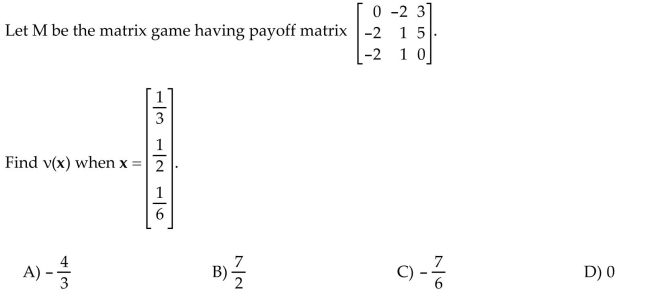
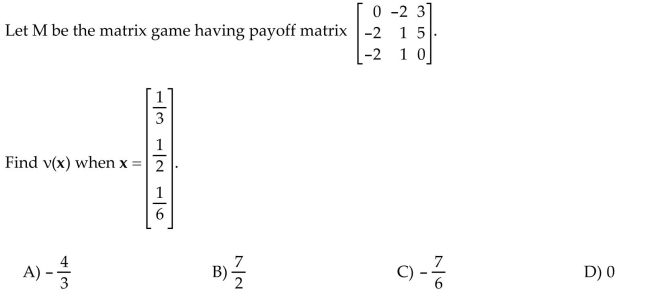

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
6
Find the value of the strategy.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
7
Find the value of the strategy.
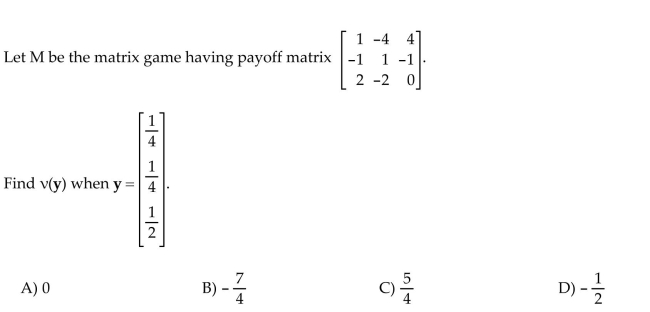
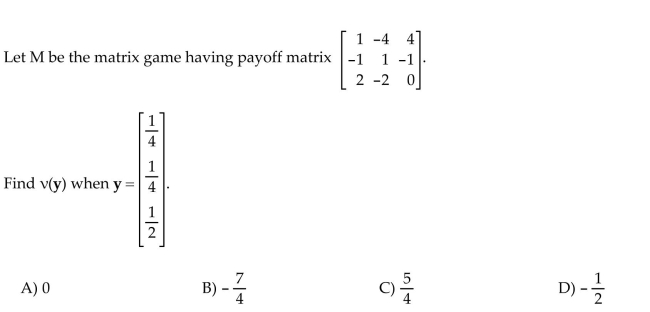

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
8
Write the payoff matrix for the game.
Player R has two cards: a red 2 and a black 7. Player C has three cards: a red 5, a black 6, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of
The two numbers. If the cards are of different colors, R receives the sum of the two numbers.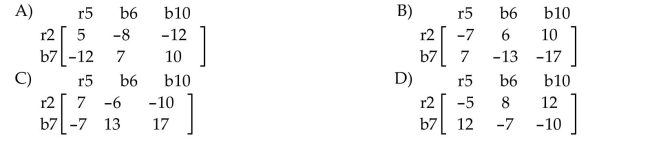
Player R has two cards: a red 2 and a black 7. Player C has three cards: a red 5, a black 6, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of
The two numbers. If the cards are of different colors, R receives the sum of the two numbers.
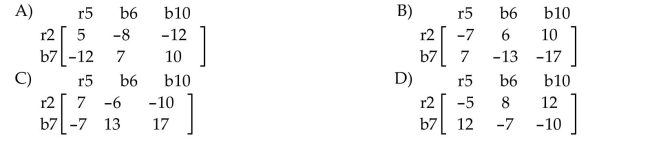

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
9
Find the expected payoff.
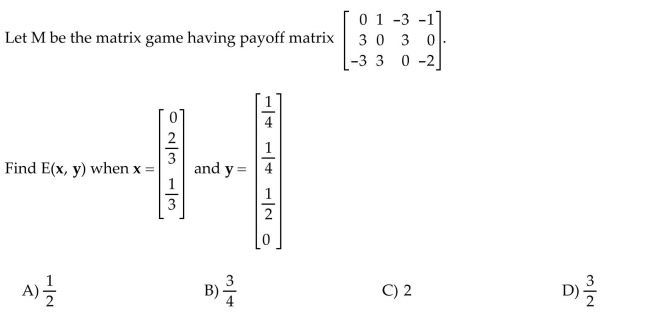


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
10
Find the expected payoff.
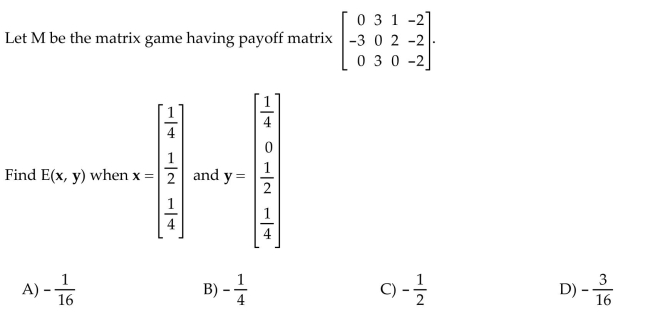


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
11
Write the payoff matrix for the game.
Players R and C each show 1, 2, or 3 fingers. If the total number N of fingers shown is even, then R pays N dollars to C. If N is odd, C pays N dollars to R.
Players R and C each show 1, 2, or 3 fingers. If the total number N of fingers shown is even, then R pays N dollars to C. If N is odd, C pays N dollars to R.


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
12
Find the expected payoff.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
13
Write the payoff matrix for the game.
Each player has a supply of nickels, dimes, and quarters. At a given signal, both players display one coin. If the displayed coins are not the same, then the player showing the higher valued coin
Gets to keep both. If they are both nickels or dimes, then player R keeps both; but if they are both
Quarters, then player C keeps both.
Each player has a supply of nickels, dimes, and quarters. At a given signal, both players display one coin. If the displayed coins are not the same, then the player showing the higher valued coin
Gets to keep both. If they are both nickels or dimes, then player R keeps both; but if they are both
Quarters, then player C keeps both.


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
14
Find all saddle points for the matrix game.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
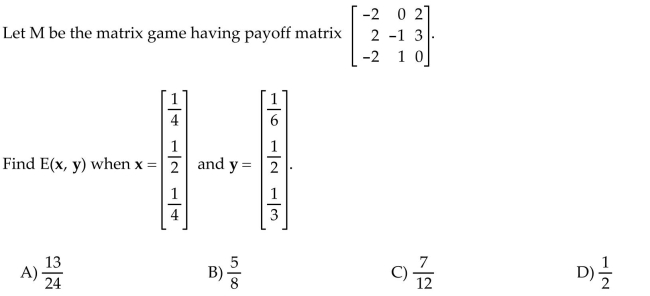
15
Find the expected payoff.


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
16
Write the payoff matrix for the game.
Each player has a supply of pennies, nickels, and dimes. At a given signal, both players display one coin. If the total number of cents N is even, then R pays N cents to C. If N is odd, then C pays
N cents to R.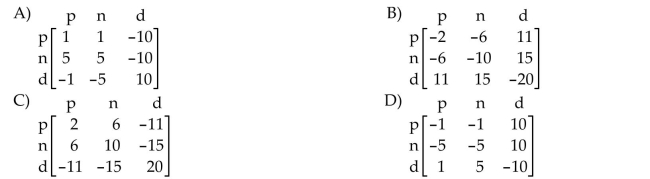
Each player has a supply of pennies, nickels, and dimes. At a given signal, both players display one coin. If the total number of cents N is even, then R pays N cents to C. If N is odd, then C pays
N cents to R.
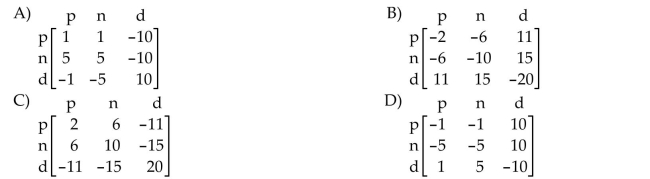

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
17
Find all saddle points for the matrix game.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
18
Find all saddle points for the matrix game.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
19
Find the value of the strategy.
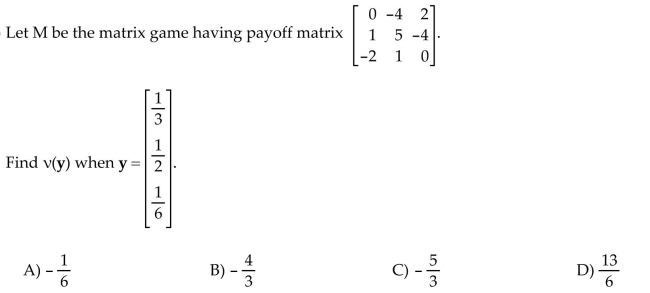
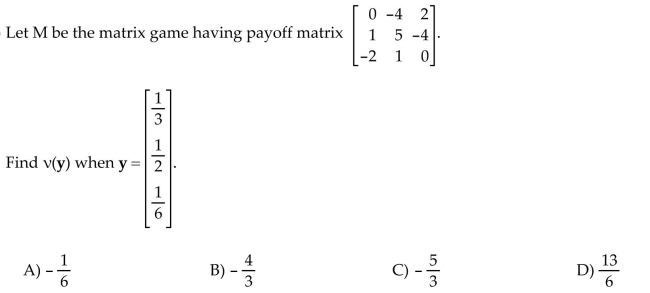

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
20
Find all saddle points for the matrix game.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the problem.
Player R has two cards: a red 2 and a black 8. Player C has three cards: a red 3, a black 5, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of
The two numbers. If the cards are of different colors, R receives the sum of the two numbers. The
Payoff matrix is :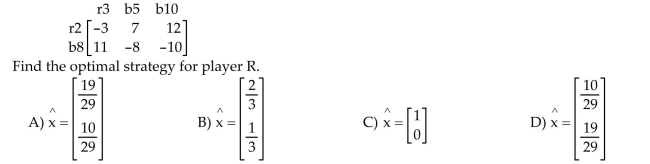
Player R has two cards: a red 2 and a black 8. Player C has three cards: a red 3, a black 5, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of
The two numbers. If the cards are of different colors, R receives the sum of the two numbers. The
Payoff matrix is :
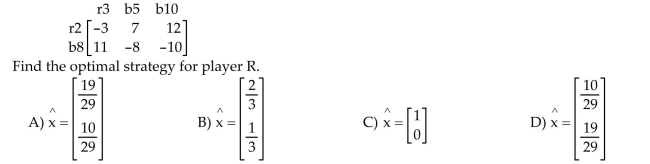

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
23
Find the value of the matrix game.
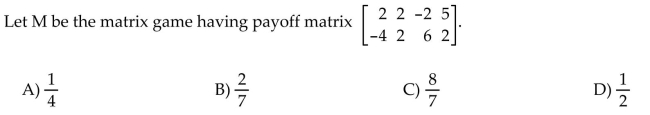
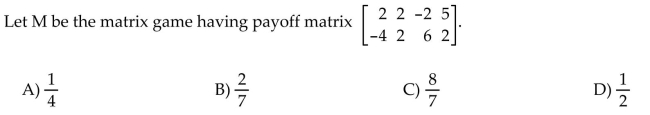

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
24
Find the value of the matrix game.
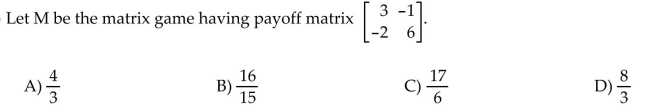
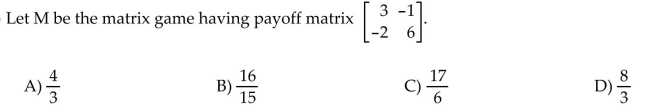

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the problem.
Each player has a supply of nickels, dimes, and quarters. At a given signal, both players display one coin. If the displayed coins are not the same, then the player showing the higher valued coin
Gets to keep both. If they are both nickels or dimes, then player R keeps both; but if they are both
Quarters, then player C keeps both. Find the optimal strategy for player C.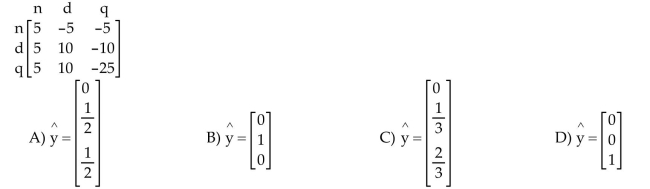
Each player has a supply of nickels, dimes, and quarters. At a given signal, both players display one coin. If the displayed coins are not the same, then the player showing the higher valued coin
Gets to keep both. If they are both nickels or dimes, then player R keeps both; but if they are both
Quarters, then player C keeps both. Find the optimal strategy for player C.
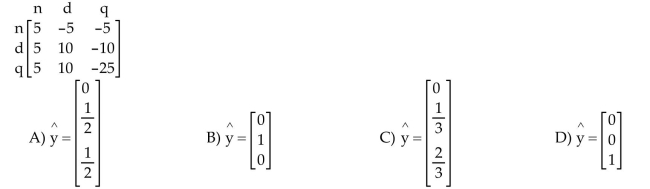

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
26
Find the optimal row or column strategy of the matrix game.
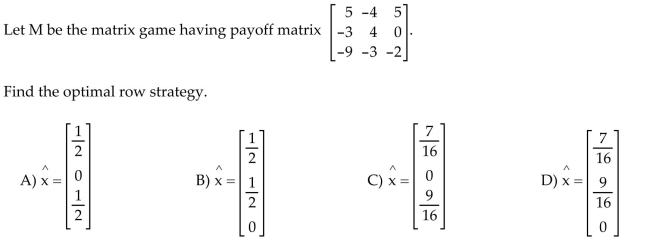
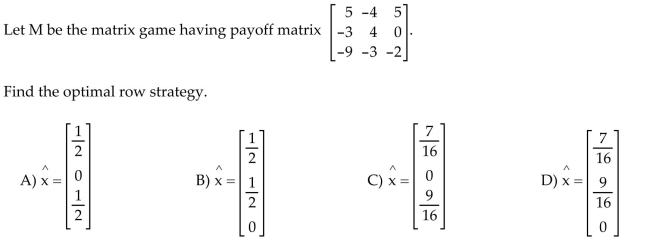

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
27
Find the value of the matrix game.
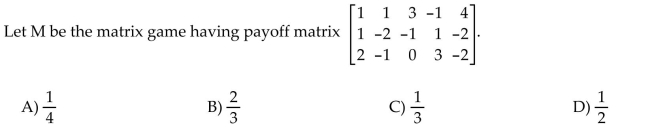
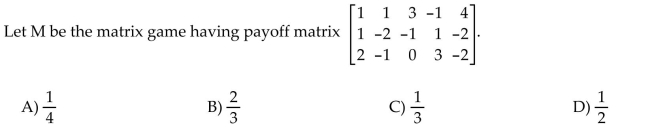

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
28
Find the optimal row or column strategy of the matrix game.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
29
Find the optimal row or column strategy of the matrix game.
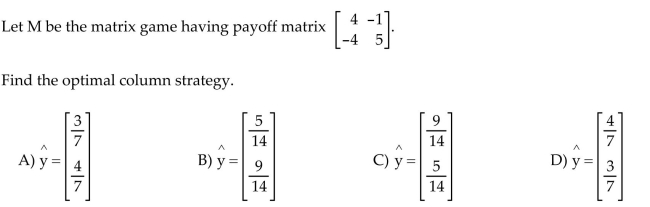
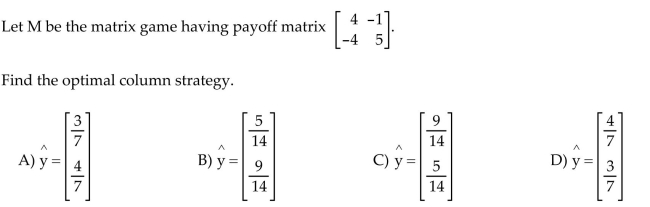

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
Player R has two cards: a red 2 and a black 8. Player C has three cards: a red 3, a black 5, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of
The two numbers. If the cards are of different colors, R receives the sum of the two numbers. The
Payoff matrix is :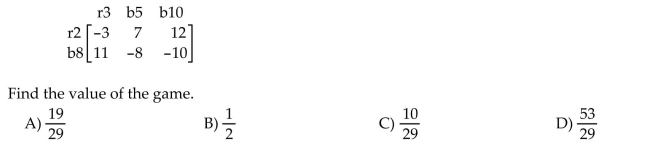
Player R has two cards: a red 2 and a black 8. Player C has three cards: a red 3, a black 5, and a black 10. They each show one of their cards. If the cards are the same color, C receives the larger of
The two numbers. If the cards are of different colors, R receives the sum of the two numbers. The
Payoff matrix is :
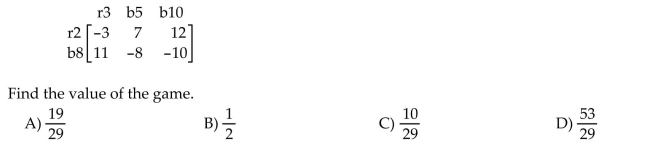

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
32
Find the optimal row or column strategy of the matrix game.
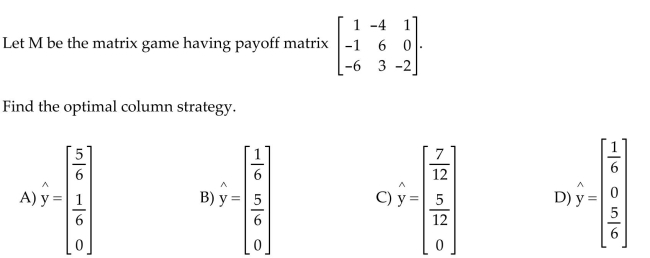
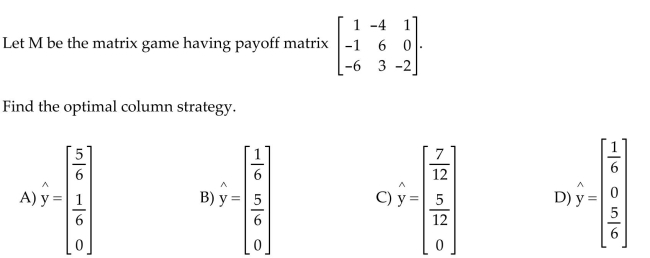

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
33
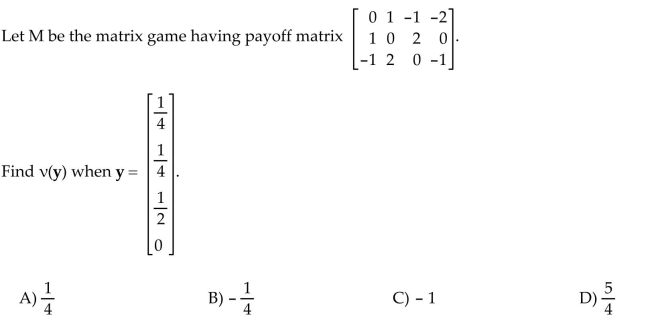
Find the value of the strategy.
 )
)
 )
)
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
34
Find the optimal row or column strategy of the matrix game.
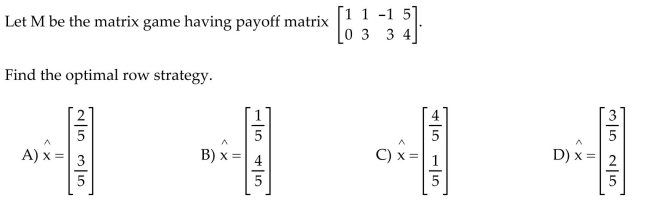
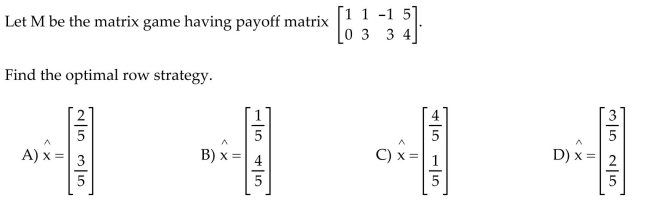

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
35
Find the optimal row or column strategy of the matrix game.
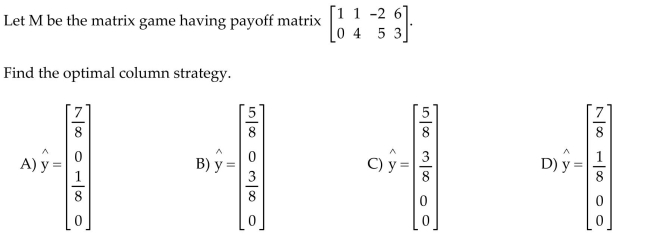


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
36
Find the value of the strategy.
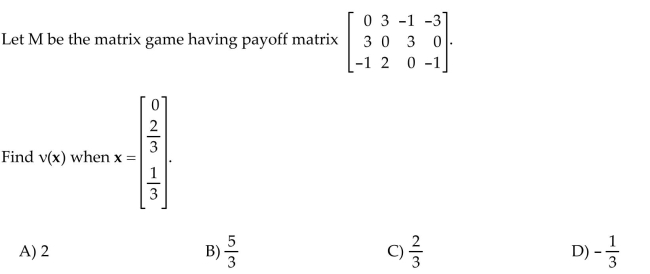
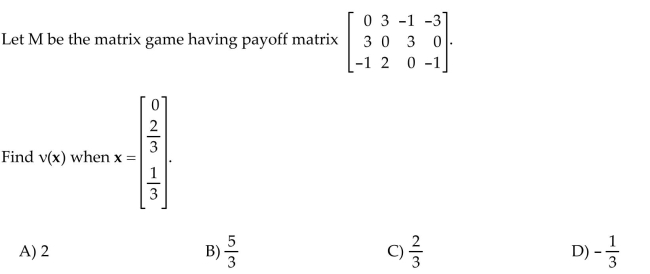

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
37
Find the optimal row or column strategy of the matrix game.
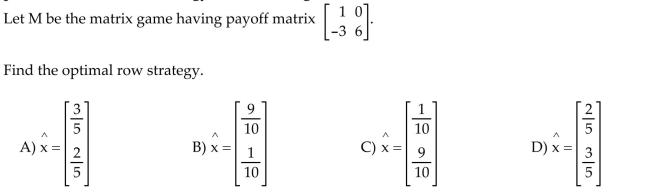
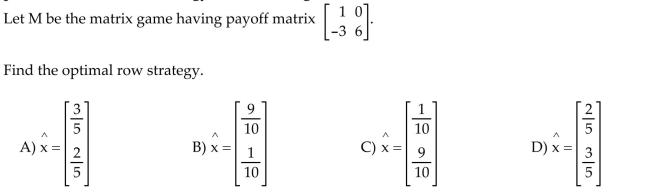

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
38
Find the optimal row or column strategy of the matrix game.
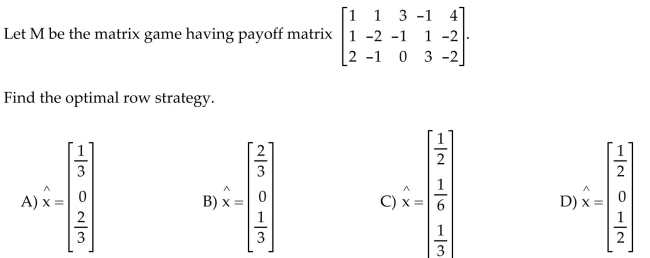
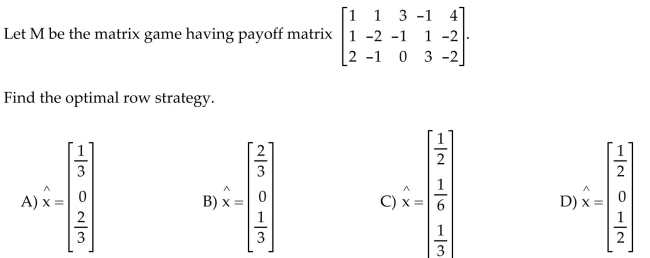

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
40
Find the value of the matrix game.
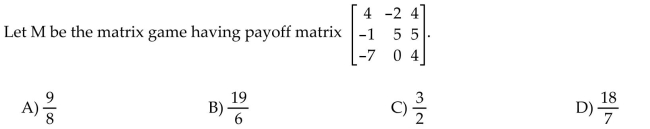
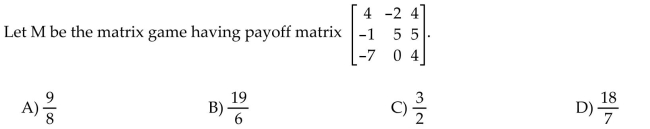

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
If the payoff matrix of a matrix game contains a saddle point, what is the optimal strategy for the column player?
A)Always choose the column with the largest maximum.
B)Always choose the column with the smallest maximum.
C)Always choose the column with the smallest minimum.
D)Always choose the column with the largest minimum.
If the payoff matrix of a matrix game contains a saddle point, what is the optimal strategy for the column player?
A)Always choose the column with the largest maximum.
B)Always choose the column with the smallest maximum.
C)Always choose the column with the smallest minimum.
D)Always choose the column with the largest minimum.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the statement is true or false.
In a matrix game, the value ν(y)of a particular strategy y to player C is equal to the minimum of
the inner product of y with each of the rows of the payoff matrix A.
In a matrix game, the value ν(y)of a particular strategy y to player C is equal to the minimum of
the inner product of y with each of the rows of the payoff matrix A.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
In a matrix game with payoff matrix A, how can you find the value ν(x)of a strategy x to row player R?
A)ν(x)is the minimum of the inner product of x with each of the columns of A.
B)ν(x)is the maximum of the inner product of x with each of the columns of A.
C)ν(x)is the maximum of the inner product of x with each of the rows of A.
D)ν(x)is the minimum of the inner product of x with each of the rows of A.
In a matrix game with payoff matrix A, how can you find the value ν(x)of a strategy x to row player R?
A)ν(x)is the minimum of the inner product of x with each of the columns of A.
B)ν(x)is the maximum of the inner product of x with each of the columns of A.
C)ν(x)is the maximum of the inner product of x with each of the rows of A.
D)ν(x)is the minimum of the inner product of x with each of the rows of A.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
44
Determine whether the statement is true or false.
In a matrix game, if row s is dominant to some other row in payoff matrix A, then row s will not be
used in some optimal strategy for row player R.
In a matrix game, if row s is dominant to some other row in payoff matrix A, then row s will not be
used in some optimal strategy for row player R.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
Anne and Michael are playing a game in which each player has a choice of two colors: green or blue. The payoff matrix with Anne as the row player is given below:
Anne and Michael are playing a game in which each player has a choice of two colors: green or blue. The payoff matrix with Anne as the row player is given below:


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
46
Determine whether the statement is true or false.
The value νC of a matrix game to player C is the maximum of the values of the various possible
strategies for C.
The value νC of a matrix game to player C is the maximum of the values of the various possible
strategies for C.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
If the payoff matrix of a matrix game contains a saddle point, what is the optimal strategy for the 45) row player?
A)Always choose the row with the largest maximum.
B)Always choose the row with the smallest minimum.
C)Always choose the row with the smallest maximum.
D)Always choose the row with the largest minimum.
If the payoff matrix of a matrix game contains a saddle point, what is the optimal strategy for the 45) row player?
A)Always choose the row with the largest maximum.
B)Always choose the row with the smallest minimum.
C)Always choose the row with the smallest maximum.
D)Always choose the row with the largest minimum.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
In a matrix game with payoff matrix A, how can you find the value ν(y)of a strategy y to player C?
A)ν(y)is the maximum of the inner product of y with each of the columns of A.
B)ν(y)is the minimum of the inner product of y with each of the columns of A.
C)ν(y)is the maximum of the inner product of y with each of the rows of A.
D)ν(y)is the minimum of the inner product of y with each of the rows of A.
In a matrix game with payoff matrix A, how can you find the value ν(y)of a strategy y to player C?
A)ν(y)is the maximum of the inner product of y with each of the columns of A.
B)ν(y)is the minimum of the inner product of y with each of the columns of A.
C)ν(y)is the maximum of the inner product of y with each of the rows of A.
D)ν(y)is the minimum of the inner product of y with each of the rows of A.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
52
Determine whether the statement is true or false.
If the payoff matrix of a matrix game contains a saddle point, the optimal strategy for each player
will be a pure strategy.
If the payoff matrix of a matrix game contains a saddle point, the optimal strategy for each player
will be a pure strategy.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
In certain situations, a matrix game can be reduced to a smaller game by deleting certain rows and/or columns from the payoff matrix. The optimal strategy for the reduced game will then
Determine the optimal strategy for the original game. In what circumstances may a row or column
Be deleted from the payoff matrix?
A)A row may be deleted if it is recessive to some other row and a column may be deleted if it is recessive to some other column.
B)A row may be deleted if it is dominant to some other row and a column may be deleted if it is recessive to some other column.
C)A row may be deleted if it is dominant to some other row and a column may be deleted if it is dominant to some other column.
D)A row may be deleted if it is recessive to some other row and a column may be deleted if it is dominant to some other column.
In certain situations, a matrix game can be reduced to a smaller game by deleting certain rows and/or columns from the payoff matrix. The optimal strategy for the reduced game will then
Determine the optimal strategy for the original game. In what circumstances may a row or column
Be deleted from the payoff matrix?
A)A row may be deleted if it is recessive to some other row and a column may be deleted if it is recessive to some other column.
B)A row may be deleted if it is dominant to some other row and a column may be deleted if it is recessive to some other column.
C)A row may be deleted if it is dominant to some other row and a column may be deleted if it is dominant to some other column.
D)A row may be deleted if it is recessive to some other row and a column may be deleted if it is dominant to some other column.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
54
Determine whether the statement is true or false.
If the payoff matrix of a matrix game contains a saddle point, the optimal strategy for the row
player will be to always choose the row with the largest minimum while the optimal strategy for
the column player will be to always choose the column with the smallest maximum.
If the payoff matrix of a matrix game contains a saddle point, the optimal strategy for the row
player will be to always choose the row with the largest minimum while the optimal strategy for
the column player will be to always choose the column with the smallest maximum.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck


