Deck 5: Induction and Recursion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/53
Play
Full screen (f)
Deck 5: Induction and Recursion
1
Prove that 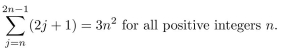
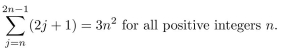
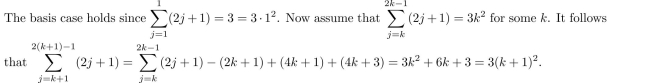
2
Use the Principle of Mathematical Induction to prove that 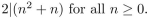
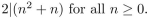
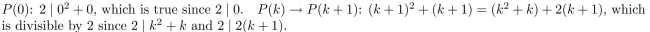
3
Use the Principle of Mathematical Induction to prove that 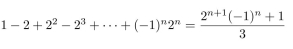 for all positive integers n .
for all positive integers n .
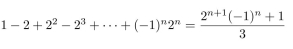 for all positive integers n .
for all positive integers n .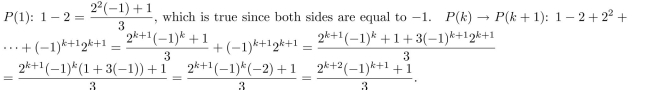
4
Use the Principle of Mathematical Induction to prove that 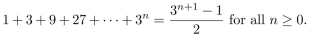
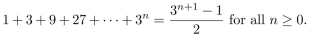

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose you wish to prove that the following is true for all positive integers n by using the Principle of Mathematical Induction: 1+3+5+...+(2 n-1)=n2 .
(a) Write P(1)
(b) Write P(72)
(c) Write P(73)
(d) Use P(72) to prove P(73)
(e) Write P(k)
(f) Write P(k+1)
(g) Use the Principle of Mathematical Induction to prove that P(n) is true for all positive integers n
(a) Write P(1)
(b) Write P(72)
(c) Write P(73)
(d) Use P(72) to prove P(73)
(e) Write P(k)
(f) Write P(k+1)
(g) Use the Principle of Mathematical Induction to prove that P(n) is true for all positive integers n

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
6
Use the Principle of Mathematical Induction to prove that 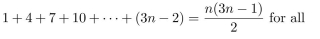 n ≥ 1.
n ≥ 1.
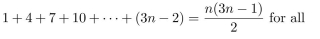 n ≥ 1.
n ≥ 1.
Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose you wish to use the Principle of Mathematical Induction to prove that 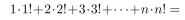
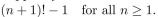
(a) Write P(1)
(b) Write P(5)
(c) Write P(k)
(d) Write P(k+1)
(e) Use the Principle of Mathematical Induction to prove that P(n) is true for all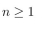
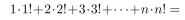
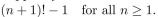
(a) Write P(1)
(b) Write P(5)
(c) Write P(k)
(d) Write P(k+1)
(e) Use the Principle of Mathematical Induction to prove that P(n) is true for all
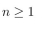

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
8
Use the Principle of Mathematical Induction to prove that 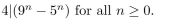
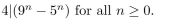

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
9
A T -omino is a tile pictured at the right. Prove that every 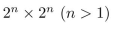 chessboard can be tiled with T-ominoes.
chessboard can be tiled with T-ominoes.
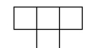
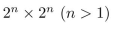 chessboard can be tiled with T-ominoes.
chessboard can be tiled with T-ominoes.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose that the only paper money consists of 3-dollar bills and 10-dollar bills. Show that any dollar amount
greater than 17 dollars could be made from a combination of these bills.
greater than 17 dollars could be made from a combination of these bills.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
11
Use the Principle of Mathematical Induction to prove that 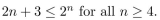
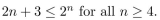

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
12
Use mathematical induction to prove that every integer amount of postage of six cents or more can be formed
using 3-cent and 4-cent stamps.
using 3-cent and 4-cent stamps.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
13
Use the Principle of Mathematical Induction to prove that 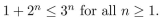
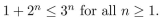

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
14
Use mathematical induction to show that n lines in the plane passing through the same point divide the plane
into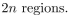
into
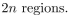

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
15
Use the Principle of Mathematical Induction to prove that 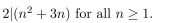
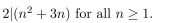

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
16
Floor borders one foot wide and of varying lengths are to be covered with nonoverlapping tiles that are available in two sizes: 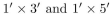 sizes. Assuming that the supply of each size is infinite, prove that every
sizes. Assuming that the supply of each size is infinite, prove that every 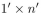 border (n > 7) can be covered with these tiles.
border (n > 7) can be covered with these tiles.
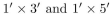 sizes. Assuming that the supply of each size is infinite, prove that every
sizes. Assuming that the supply of each size is infinite, prove that every 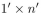 border (n > 7) can be covered with these tiles.
border (n > 7) can be covered with these tiles.
Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
17
Use the Principle of Mathematical Induction to prove that 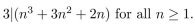
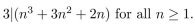

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
18
Use the Principle of Mathematical Induction to prove that 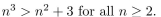
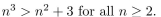

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
19
Let 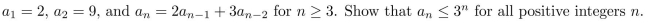
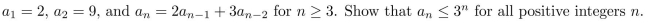

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
20
Use the Principle of Mathematical Induction to prove that any integer amount of postage from 18 cents on
up can be made from an infinite supply of 4-cent and 7-cent stamps.
up can be made from an infinite supply of 4-cent and 7-cent stamps.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
21
In questions give a recursive definition with initial condition(s).
The sequence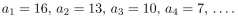
The sequence
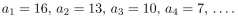

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
22
In questions give a recursive definition with initial condition(s).
The set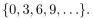
The set
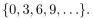

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
23
In questions give a recursive definition with initial condition(s).
The function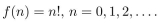
The function
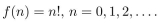

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
24
give a recursive definition (with initial condition(s)) of 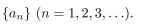
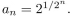
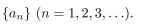
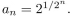

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
25
Prove that 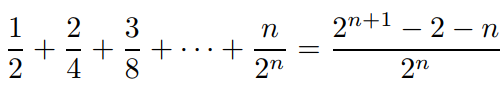 for all
for all 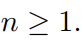
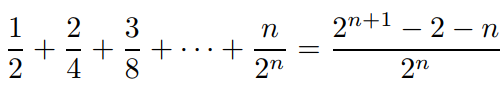 for all
for all 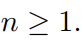

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
26
In questions give a recursive definition with initial condition(s).
The function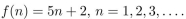
The function
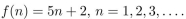

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
27
give a recursive definition (with initial condition(s)) of 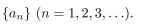
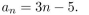
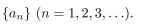
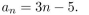

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
28
In questions give a recursive definition with initial condition(s) of the set S.
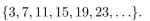
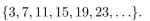

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
29
give a recursive definition (with initial condition(s)) of 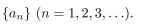
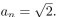
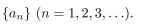
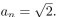

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
30
give a recursive definition (with initial condition(s)) of 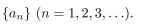
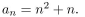
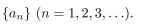
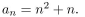

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
31
In questions give a recursive definition with initial condition(s).
The Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, . . . .
The Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, . . . .

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
32
give a recursive definition (with initial condition(s)) of 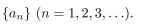
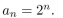
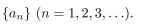
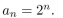

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
33
Use the Principle of Mathematical Induction to prove that 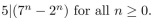
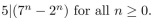

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
34
In questions give a recursive definition with initial condition(s).
The set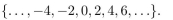
The set
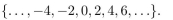

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
35
Prove that all distributive law 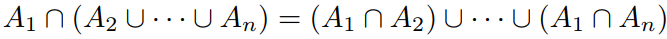 is true for all
is true for all 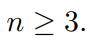
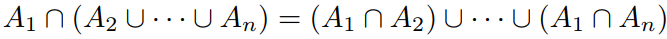 is true for all
is true for all 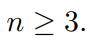

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
36
give a recursive definition (with initial condition(s)) of 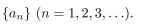
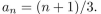
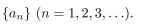
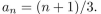

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
37
In questions give a recursive definition with initial condition(s).
The function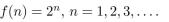
The function
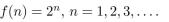

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
38
In questions give a recursive definition with initial condition(s).
The set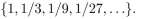
The set
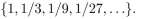

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
39
Find the error in the following proof of this "theorem":
"Theorem: Every positive integer equals the next largest positive integer."
"Proof: Let P(n) be the proposition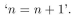
To show that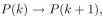 assume that P(k) is true for some k , so that k=k+1 . Add 1 to both sides of this equation to obtain k+1=k+2 , which is P(k+1) . Therefore
assume that P(k) is true for some k , so that k=k+1 . Add 1 to both sides of this equation to obtain k+1=k+2 , which is P(k+1) . Therefore 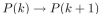 is true. Hence P(n) is true for all positive integers n . "
is true. Hence P(n) is true for all positive integers n . "
"Theorem: Every positive integer equals the next largest positive integer."
"Proof: Let P(n) be the proposition
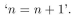
To show that
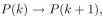 assume that P(k) is true for some k , so that k=k+1 . Add 1 to both sides of this equation to obtain k+1=k+2 , which is P(k+1) . Therefore
assume that P(k) is true for some k , so that k=k+1 . Add 1 to both sides of this equation to obtain k+1=k+2 , which is P(k+1) . Therefore 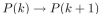 is true. Hence P(n) is true for all positive integers n . "
is true. Hence P(n) is true for all positive integers n . " 
Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
40
In questions give a recursive definition with initial condition(s).
The set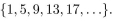
The set
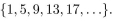

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
41
In questions give a recursive definition with initial condition(s) of the set S.
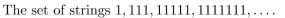
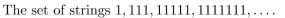

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
42
In questions give a recursive definition with initial condition(s) of the set S.
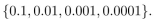
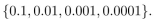

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
43
Find f(2) and f(3) if 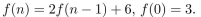

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
44
Describe a recursive algorithm for computing 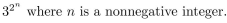

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the following program segment: 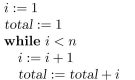
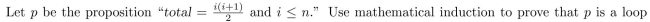 invariant.
invariant.
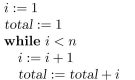
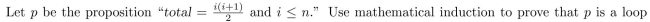 invariant.
invariant.
Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
46
Give a recursive algorithm for computing 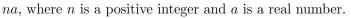
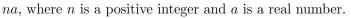

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
47
Verify that the following program segment is correct with respect to the initial assertion T and the final
assertion (x ≤ y ∧ max = y) ∨ (x > y ∧ max = x):
if x ≤ y then
max := y
else
max := x
assertion (x ≤ y ∧ max = y) ∨ (x > y ∧ max = x):
if x ≤ y then
max := y
else
max := x

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
48
In questions give a recursive definition with initial condition(s) of the set S.
All positive integer multiples of 5.
All positive integer multiples of 5.

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
49
Verify that the program segment 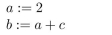 is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
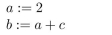 is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
50
Find f(2) and f(3) if f(n)=f(n-1) / f(n-2), f(0)=2, f(1)=5 .

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
51
Find f(2) and f(3) if 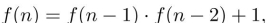 f(0)=1, f(1)=4
f(0)=1, f(1)=4
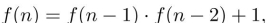 f(0)=1, f(1)=4
f(0)=1, f(1)=4 
Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose 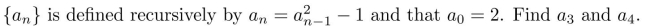
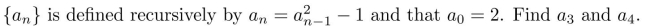

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck
53
In questions give a recursive definition with initial condition(s) of the set S.
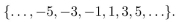
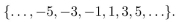

Unlock Deck
Unlock for access to all 53 flashcards in this deck.
Unlock Deck
k this deck


