Deck 10: Graphs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/127
Play
Full screen (f)
Deck 10: Graphs
1
In questions fill in the blanks.1113:1156
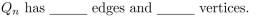
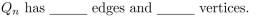
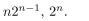
2
Many supermarkets use loyalty or discount cards to keep track of who buys which items. How can graphs
be used to model this relationship? Should the edges be directed or undirected? Should multiple edges be
allowed? Should loops be allowed? Does this graph have any special properties?
be used to model this relationship? Should the edges be directed or undirected? Should multiple edges be
allowed? Should loops be allowed? Does this graph have any special properties?
Use vertices to represent the customers and the items stocked. An edge connecting a customer u to an item
v is drawn if u buys v. Multiple edges are allowed, since customers can buy several items of the same kind.
Note that the graph is bipartite.
v is drawn if u buys v. Multiple edges are allowed, since customers can buy several items of the same kind.
Note that the graph is bipartite.
3
Construct a call graph for five friends Alice, Bob, Charlie, Diane and Evan, if there were three calls from Alice
to Bob, two calls from Alice to Diane, five calls from Alice to Evan, one call from Bob to Alice, three calls
from Charlie to Alice, one call from Charlie to Evan, one call from Diane to Charlie, and one call from Evan
to Diane.
to Bob, two calls from Alice to Diane, five calls from Alice to Evan, one call from Bob to Alice, three calls
from Charlie to Alice, one call from Charlie to Evan, one call from Diane to Charlie, and one call from Evan
to Diane.
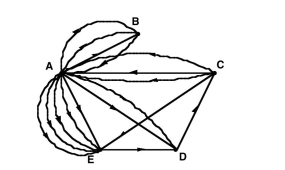
4
In questions fill in the blanks.1113:1156
The length of the longest simple circuit in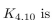 .
.
The length of the longest simple circuit in
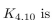 .
.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
5
for each graph give an ordered pair description (vertex set and edge set) and an adjacency
matrix, and draw a picture of the graph.
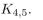
matrix, and draw a picture of the graph.
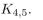

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
6
In questions fill in the blanks.1113:1156
The adjacency matrix for
The adjacency matrix for


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
7
In questions fill in the blanks.1113:1156
The length of the longest simple circuit in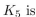 .
.
The length of the longest simple circuit in
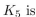 .
.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
8
In the group stage of the 2011 women's soccer world cup the USA beat North Korea, Sweden beat Columbia,
the USA beat Columbia, Sweden beat North Korea, Sweden beat the USA, and the game between Columbia
and North Korea ended in a tie. Model this outcome using a directed segment from A to B if A beat B, and
an undirected segment if the game ended in a tie.
the USA beat Columbia, Sweden beat North Korea, Sweden beat the USA, and the game between Columbia
and North Korea ended in a tie. Model this outcome using a directed segment from A to B if A beat B, and
an undirected segment if the game ended in a tie.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
9
for each graph give an ordered pair description (vertex set and edge set) and an adjacency
matrix, and draw a picture of the graph.
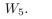
matrix, and draw a picture of the graph.
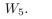

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
10
for each graph give an ordered pair description (vertex set and edge set) and an adjacency
matrix, and draw a picture of the graph.
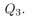
matrix, and draw a picture of the graph.
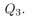

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
11
In questions fill in the blanks.1113:1156
List all positive integers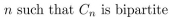 .
.
List all positive integers
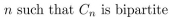 .
.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
12
During the construction of a home there are certain tasks that have to be completed before another one can
commence, e.g., the roof has to be installed before the work on electrical wiring or plumbing can begin. How
can a graph be used to model the different tasks during the construction? Should the edges be directed or
undirected? Looking at the graph model, how can we find tasks that can be done at any time and how can
we find tasks that do not have to be completed before other tasks can begin?
commence, e.g., the roof has to be installed before the work on electrical wiring or plumbing can begin. How
can a graph be used to model the different tasks during the construction? Should the edges be directed or
undirected? Looking at the graph model, how can we find tasks that can be done at any time and how can
we find tasks that do not have to be completed before other tasks can begin?

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
13
In questions fill in the blanks.1113:1156
The adjacency matrix for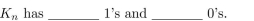
The adjacency matrix for
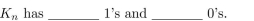

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
14
In questions fill in the blanks.1113:1156
 .
.
 .
.
Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
15
In questions fill in the blanks.1113:1156
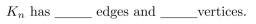
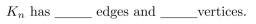

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
16
for each graph give an ordered pair description (vertex set and edge set) and an adjacency
matrix, and draw a picture of the graph.
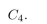
matrix, and draw a picture of the graph.
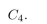

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
17
Explain how graphs can be used to model the spread of a contagious disease. Should the edges be directed or
undirected? Should multiple edges be allowed? Should loops be allowed?
undirected? Should multiple edges be allowed? Should loops be allowed?

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
18
In questions fill in the blanks.1113:1156
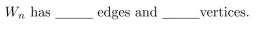
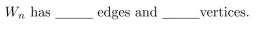

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
19
In questions fill in the blanks.1113:1156
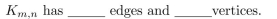
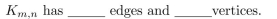

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
20
for each graph give an ordered pair description (vertex set and edge set) and an adjacency
matrix, and draw a picture of the graph.
K6.
matrix, and draw a picture of the graph.
K6.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
21
In questions fill in the blanks.1113:1156
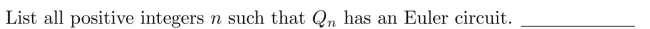
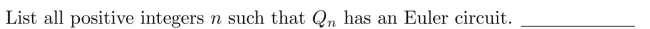

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
22
In questions fill in the blanks.1113:1156
There are non-isomorphic simple digraphs with 3 vertices and 2 edges.
There are non-isomorphic simple digraphs with 3 vertices and 2 edges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
23
In questions fill in the blanks.1113:1156
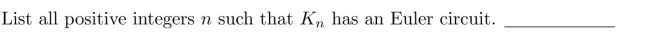
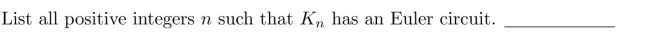

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
24
In questions fill in the blanks.1113:1156
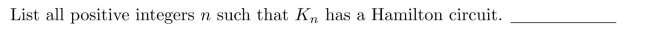
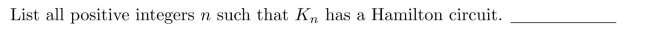

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
25
In questions fill in the blanks.1113:1156
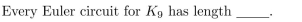
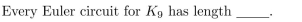

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
26
In questions fill in the blanks.1113:1156
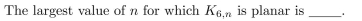
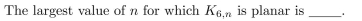

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
27
In questions fill in the blanks.1113:1156
List all positive integers n such that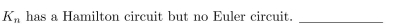
List all positive integers n such that
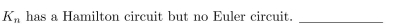

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
28
In questions fill in the blanks.1113:1156
The adjacency matrix for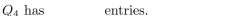
The adjacency matrix for
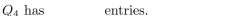

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
29
In questions fill in the blanks.1113:1156
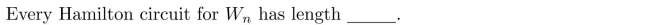
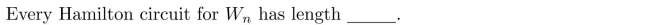

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
30
In questions fill in the blanks.1113:1156
The incidence matrix for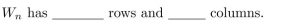
The incidence matrix for
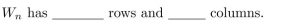

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
31
In questions fill in the blanks.1113:1156
There are non-isomorphic simple graphs with 3 vertices.
There are non-isomorphic simple graphs with 3 vertices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
32
In questions fill in the blanks.1113:1156
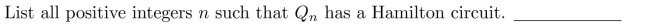
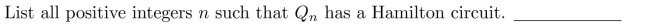

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
33
In questions fill in the blanks.1113:1156
The incidence matrix for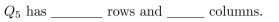
The incidence matrix for
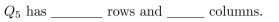

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
34
In questions fill in the blanks.1113:1156
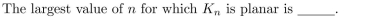
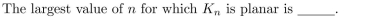

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
35
In questions fill in the blanks.1113:1156
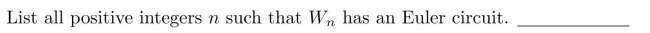
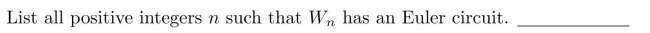

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
36
In questions fill in the blanks.1113:1156
There are 0's and 1's in the adjacency matrix for Cn.
There are 0's and 1's in the adjacency matrix for Cn.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
37
In questions fill in the blanks.1113:1156
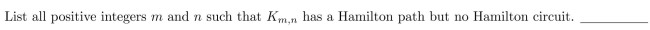
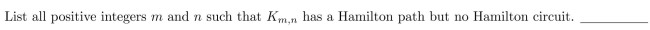

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
38
In questions fill in the blanks.1113:1156
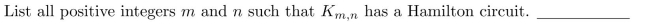
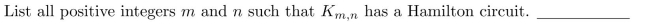

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
39
In questions fill in the blanks.1113:1156
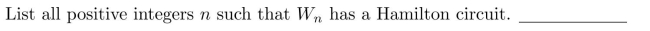
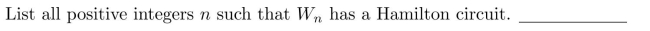

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
40
In questions fill in the blanks.1113:1156
There are non-isomorphic simple undirected graphs with 5 vertices and 3 edges.
There are non-isomorphic simple undirected graphs with 5 vertices and 3 edges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
41
In questions fill in the blanks.1113:1156
Determine whether the graph is strongly connected, and if not, whether it is weakly connected.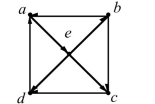
Determine whether the graph is strongly connected, and if not, whether it is weakly connected.


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the graph is strongly connected, and if not, whether it is weakly connected. 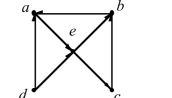


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
43
In questions fill in the blanks.1113:1156
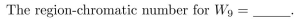
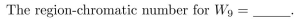

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
44
In questions fill in the blanks.1113:1156
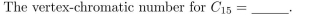
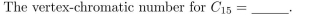

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
45
Find the strongly connected components of the graph. 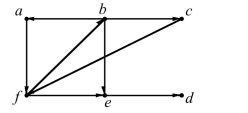


Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
46
In questions fill in the blanks.1113:1156
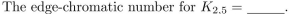
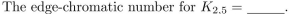

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
47
In questions fill in the blanks.1113:1156
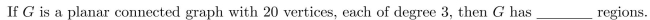
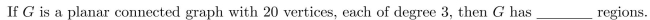

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
48

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
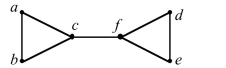
49
In questions fill in the blanks.1113:1156
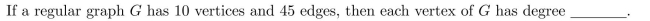
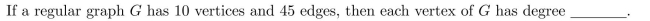

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
50
In questions fill in the blanks.1113:1156
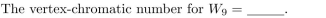
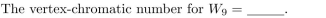

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
51
In questions fill in the blanks.1113:1156
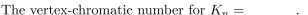
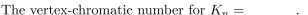

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
52
In questions fill in the blanks.1113:1156
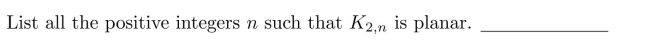
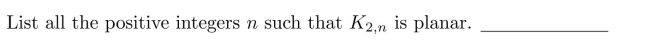

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
53
In questions either give an example or prove that there are none.
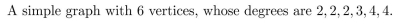
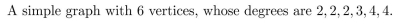

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
54
In questions fill in the blanks.1113:1156
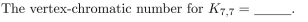
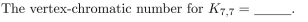

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
55
Find the strongly connected components of the graph. 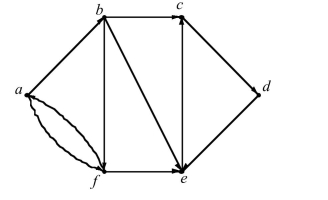

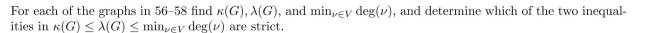

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
56
In questions fill in the blanks.1113:1156
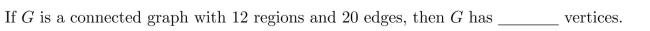
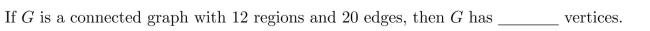

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
57
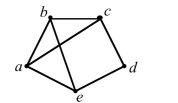

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
58
In questions fill in the blanks.1113:1156
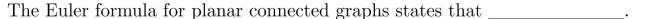
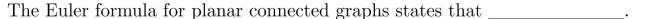

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
59
In questions either give an example or prove that there are none.
A simple graph with 8 vertices, whose degrees are 0, 1, 2, 3, 4, 5, 6, 7.
A simple graph with 8 vertices, whose degrees are 0, 1, 2, 3, 4, 5, 6, 7.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
60
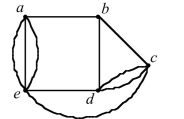

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
61
In questions either give an example or prove that there are none.
A graph with 9 vertices with edge-chromatic number equal to 2.
A graph with 9 vertices with edge-chromatic number equal to 2.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
62
In questions either give an example or prove that there are none.
A graph with 6 vertices that has an Euler circuit but no Hamilton circuit.
A graph with 6 vertices that has an Euler circuit but no Hamilton circuit.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
63
In questions either give an example or prove that there are none.
A connected simple planar graph with 5 regions and 8 vertices, each of degree 3.
A connected simple planar graph with 5 regions and 8 vertices, each of degree 3.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
64
In questions either give an example or prove that there are none.
A simple digraph with indegrees 1, 1, 1 and outdegrees 1, 1, 1.
A simple digraph with indegrees 1, 1, 1 and outdegrees 1, 1, 1.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
65
In questions either give an example or prove that there are none.
A simple digraph with indegrees 0, 1, 2 and outdegrees 0, 1, 2.
A simple digraph with indegrees 0, 1, 2 and outdegrees 0, 1, 2.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
66
In questions either give an example or prove that there are none.
A simple digraph with indegrees 0, 1, 1, 2 and outdegrees 0, 1, 1, 1.
A simple digraph with indegrees 0, 1, 1, 2 and outdegrees 0, 1, 1, 1.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
67
In questions either give an example or prove that there are none.
A graph with 7 vertices that has a Hamilton circuit but no Euler circuit.
A graph with 7 vertices that has a Hamilton circuit but no Euler circuit.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
68
In questions either give an example or prove that there are none.
A graph with a Hamilton path but no Hamilton circuit.
A graph with a Hamilton path but no Hamilton circuit.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
69
In questions either give an example or prove that there are none.
A simple graph with 6 vertices and 16 edges.
A simple graph with 6 vertices and 16 edges.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
70
In questions either give an example or prove that there are none.
A graph with region-chromatic number equal to 6.
A graph with region-chromatic number equal to 6.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
71
In questions either give an example or prove that there are none.
A simple digraph with indegrees 0, 1, 2, 2 and outdegrees 0, 1, 1, 3.
A simple digraph with indegrees 0, 1, 2, 2 and outdegrees 0, 1, 1, 3.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
72
In questions either give an example or prove that there are none.
A simple graph with degrees 1, 2, 2, 3.
A simple graph with degrees 1, 2, 2, 3.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
73
In questions either give an example or prove that there are none.
A simple graph with degrees 1, 1, 2, 4.
A simple graph with degrees 1, 1, 2, 4.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
74
In questions either give an example or prove that there are none.
A simple digraph with indegrees: 0, 1, 2, 2, 3, 4 and outdegrees: 1, 1, 2, 2, 3, 4.
A simple digraph with indegrees: 0, 1, 2, 2, 3, 4 and outdegrees: 1, 1, 2, 2, 3, 4.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
75
In questions either give an example or prove that there are none.
A graph with a Hamilton circuit but no Hamilton path.
A graph with a Hamilton circuit but no Hamilton path.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
76
In questions either give an example or prove that there are none.
A planar graph with 10 vertices.
A planar graph with 10 vertices.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
77
In questions either give an example or prove that there are none.
A graph with 4 vertices that is not planar.
A graph with 4 vertices that is not planar.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
78
In questions either give an example or prove that there are none.
A graph with vertex-chromatic number equal to 6.
A graph with vertex-chromatic number equal to 6.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
79
In questions either give an example or prove that there are none.
A simple graph with degrees 2, 3, 4, 4, 4.
A simple graph with degrees 2, 3, 4, 4, 4.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck
80
In questions either give an example or prove that there are none.
A simple digraph with indegrees 0, 1, 2, 4, 5 and outdegrees 0, 3, 3, 3, 3.
A simple digraph with indegrees 0, 1, 2, 4, 5 and outdegrees 0, 3, 3, 3, 3.

Unlock Deck
Unlock for access to all 127 flashcards in this deck.
Unlock Deck
k this deck


