Deck 8: Sequences, Series, Induction, and Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/270
Play
Full screen (f)
Deck 8: Sequences, Series, Induction, and Probability
1
An sequence is a sequence in which consecutive terms alternate in sign.
alternating
2
The nth term of a sequence is given. Find the indicated term.
A) 73
B) 576
C) 108
D) 21
A) 73
B) 576
C) 108
D) 21
A
3
Given , the variable i is called the of . The value 1 is called the
limit of summation. The value n is called the upper of summation.
limit of summation. The value n is called the upper of summation.
index; summation; lower; limit
4
Choose the one alternative that best completes the statement or answers the question.
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
В)
C)
D)
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
5
For the expression 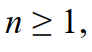 represents the product of the first n positive integers
represents the product of the first n positive integers
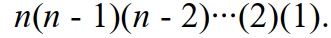 , For n = 0 we have 0!=
, For n = 0 we have 0!=
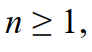 represents the product of the first n positive integers
represents the product of the first n positive integers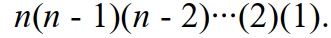 , For n = 0 we have 0!=
, For n = 0 we have 0!= 
Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
6
Choose the one alternative that best completes the statement or answers the question.
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
7
Write the first five terms of the sequence defined recursively.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
8
Write the first five terms of the sequence defined recursively.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate the expression.
A) 24
B) 1
C) 126
D) 362,736
A) 24
B) 1
C) 126
D) 362,736

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
10
Choose the one alternative that best completes the statement or answers the question.
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
11
The nth term of a sequence is given. Find the indicated term.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
12
One property of summation indicates that

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
13
A formula defines the nth term of a sequence as a function of one or more terms
preceding it.
preceding it.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
14
Choose the one alternative that best completes the statement or answers the question.
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
15
Choose the one alternative that best completes the statement or answers the question.
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
В)
C)
D)
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
16
Given an infinite sequence , … the sum of the terms of the sequence is called an
infinite . The notation is called the nth of the sequence and is
called a finite series.
infinite . The notation is called the nth of the sequence and is
called a finite series.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
17
Choose the one alternative that best completes the statement or answers the question.
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)
The nth term of a sequence is given. Write the first four terms of the sequence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
18
Write the first five terms of the sequence defined recursively.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
19
An infinite is a function whose domain is the set of positive integers. A
sequence is a function whose domain is the set of the first n positive integers.
sequence is a function whose domain is the set of the first n positive integers.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
20
The expression is called the term or general term of a sequence.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
21
The nth term of a sequence is given. Find the indicated term.
A)
B)
C) 2
D)
A)
B)
C) 2
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
22
Find the sum.
A) 35
B) 50
C) 59
D) 74
A) 35
B) 50
C) 59
D) 74

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
23
Find the sum.
A) 110
B) 36
C) 48
D) 120
A) 110
B) 36
C) 48
D) 120

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
24
Find the sum.
A) 1,035
в) 7
C) 315
D) 308
A) 1,035
в) 7
C) 315
D) 308

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
25
Find the nth term of a sequence whose first four terms are given.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
27
Find the nth term of a sequence whose first four terms are given.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
28
Find the nth term of a sequence whose first four terms are given.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
29
Find the sum.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
30
Find the sum.
A)
B) 540
C)
D) 1,764
A)
B) 540
C)
D) 1,764

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
31
The nth term of a sequence is given. Find the indicated term.
A) 8064
B)
C) 145,152
D)
A) 8064
B)
C) 145,152
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
32
Find the nth term of a sequence whose first four terms are given.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
33
Find the sum.
A)
B) 84
C) 12
D)
A)
B) 84
C) 12
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
34
Find the sum.
A)
B) 45
C)
D)
A)
B) 45
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate the expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
36
Write the sum using summation notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
37
Find the nth term of a sequence whose first four terms are given.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
38
Find the sum.
A) 21
B) 54
C) 27
D) 33
A) 21
B) 54
C) 27
D) 33

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
39
Write the sum using summation notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
40
Find the sum.
A) 130
B) 250
C) 70
D) 1,200
A) 130
B) 250
C) 70
D) 1,200

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
41
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The difference between consecutive terms in an arithmetic sequence is called the
, and is denoted by d.
Provide the missing information.
The difference between consecutive terms in an arithmetic sequence is called the
, and is denoted by d.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
42
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
An arithmetic sequence is a linear function whose domain is the set of integers.
Provide the missing information.
An arithmetic sequence is a linear function whose domain is the set of integers.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
43
Write the sum using summation notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
44
Choose the one alternative that best completes the statement or answers the question.
Solve the problem.
In a business meeting, every person at the meeting shakes every other person's hand exactly one time. The total number of handshakes for n people at the meeting is given by Evaluate and interpret its meaning in the context of this problem.
A) 132; If 12 people are present at the meeting there will be 132 handshakes.
B) 66; If 12 people are present at the meeting there will be 66 handshakes.
C) 11; The 12th person shakes performs 11 handshakes.
D) 78; If 12 people are present at the meeting there will be 78 handshakes.
Solve the problem.
In a business meeting, every person at the meeting shakes every other person's hand exactly one time. The total number of handshakes for n people at the meeting is given by Evaluate and interpret its meaning in the context of this problem.
A) 132; If 12 people are present at the meeting there will be 132 handshakes.
B) 66; If 12 people are present at the meeting there will be 66 handshakes.
C) 11; The 12th person shakes performs 11 handshakes.
D) 78; If 12 people are present at the meeting there will be 78 handshakes.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
45
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
An sequence is a sequence in which each term after the first differs from its predecessor
by a fixed constant.
Provide the missing information.
An sequence is a sequence in which each term after the first differs from its predecessor
by a fixed constant.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
46
Choose the one alternative that best completes the statement or answers the question.
Determine whether the sequence is arithmetic. If so, find the common difference.
4, -16, 64, -256, . . .
A) not arithmetic
B) arithmetic; d = -4
C) arithmetic; d = 4
D) arithmetic; d = -2
Determine whether the sequence is arithmetic. If so, find the common difference.
4, -16, 64, -256, . . .
A) not arithmetic
B) arithmetic; d = -4
C) arithmetic; d = 4
D) arithmetic; d = -2

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
47
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
Given an arithmetic sequence with first term , and common difference d, the nth term is
represented by the formula .
Provide the missing information.
Given an arithmetic sequence with first term , and common difference d, the nth term is
represented by the formula .

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
48
Write the first four terms of an arithmetic sequence, , based on the given information about the
sequence.
A)
B)
C)
D)
sequence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
49
Write the sum using summation notation.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
50
Choose the one alternative that best completes the statement or answers the question.
Determine whether the sequence is arithmetic. If so, find the common difference.
A) arithmetic;
B) not arithmetic
C) arithmetic;
D) arithmetic;
Determine whether the sequence is arithmetic. If so, find the common difference.
A) arithmetic;
B) not arithmetic
C) arithmetic;
D) arithmetic;

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
51
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
Given an arithmetic sequence with first term a1 and nth term an, the nth partial sum is given by the
formula
Provide the missing information.
Given an arithmetic sequence with first term a1 and nth term an, the nth partial sum is given by the
formula


Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
52
Write the sum using summation notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
53
Write the first four terms of the arithmetic sequence with the given first term and common difference.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the problem.
Expenses for a company for year 1 are . Every year thereafter, expenses increase by plus of the cost of the prior year. Let represent the original cost for year 1 ; that is .
Use a recursive formula to find the cost in terms of for each subsequent year, .
A)
B)
C)
D)
Expenses for a company for year 1 are . Every year thereafter, expenses increase by plus of the cost of the prior year. Let represent the original cost for year 1 ; that is .
Use a recursive formula to find the cost in terms of for each subsequent year, .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
55
Write the sum using summation notation.
A)
B)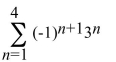
C)
D)
A)
B)
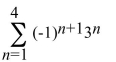
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
56
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The sum of the first n terms of a sequence is called the nth sum and is denoted by
Provide the missing information.
The sum of the first n terms of a sequence is called the nth sum and is denoted by

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
57
Rewrite the series as an equivalent series with the new index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
58
Write the sum using summation notation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
59
Use the provided sums to evaluate the given expression.
and evaluate
A) 118,080
B) 22,960
C) 111,520
D) 203,360
and evaluate
A) 118,080
B) 22,960
C) 111,520
D) 203,360

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
60
Write the first four terms of an arithmetic sequence, , based on the given information about the
sequence.
Write the first five terms of the arithmetic sequence.
A)
B)
C)
D)
sequence.
Write the first five terms of the arithmetic sequence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
A student studying to be a veterinarian's assistant keeps track of a kitten's weight each week for a 5-week period after birth. a. Write an expression for the nth term of the sequence representing the kitten's weight, n weeks after birth.
B) If the weight of the kitten continues to increase linearly for 3 months, predict the kitten's weight 10 weeks
After birth. A) a.
b.
B) a.
b.
C) a.
b.
D) a.
b.
A student studying to be a veterinarian's assistant keeps track of a kitten's weight each week for a 5-week period after birth. a. Write an expression for the nth term of the sequence representing the kitten's weight, n weeks after birth.
B) If the weight of the kitten continues to increase linearly for 3 months, predict the kitten's weight 10 weeks
After birth. A) a.
b.
B) a.
b.
C) a.
b.
D) a.
b.

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
62
Find the indicated term of the arithmetic sequence based on the given information.
Find
A)
B)
C)
D)
Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
63
Write a nonrecursive formula for the nth term of the arithmetic sequence {an} based on the given
information.
A)
B)
C)
D)
information.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
64
Find the number of terms of the finite arithmetic sequence.
A) 48
В) 50
C) 51
D) 49
A) 48
В) 50
C) 51
D) 49

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
65
Find the indicated term of the arithmetic sequence based on the given information.
and Find
A)
B)
C)
D)
and Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
66
Find the indicated term.
Find
A)
B)
C)
D)
Find
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
67
Write a recursive formula to define the sequence.
A) and for
B) and for
C) and for
D) and for
A) and for
B) and for
C) and for
D) and for

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
68
Find the indicated term of the arithmetic sequence based on the given information.
and Find
A) 631
B) 671
C) 625
D) 637
and Find
A) 631
B) 671
C) 625
D) 637

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
69
Find the indicated term of the arithmetic sequence based on the given information.
and Find .
A)
B)
C)
D)
and Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
A physical activity class requires students to jog around an indoor track. For the first week of class the students jog 300 m around the track each day. Each week thereafter, the students increase the
Distance jogged by 125 m. Write the nth term of a sequence defining the number of meters jogged
Each day by the students in the nth week of class. A)
В)
C)
D)
A physical activity class requires students to jog around an indoor track. For the first week of class the students jog 300 m around the track each day. Each week thereafter, the students increase the
Distance jogged by 125 m. Write the nth term of a sequence defining the number of meters jogged
Each day by the students in the nth week of class. A)
В)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
71
Write a recursive formula to define the sequence.
A) and for
B) and for
C) and for
D) and for
A) and for
B) and for
C) and for
D) and for

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
72
Write a nonrecursive formula for the nth term of the arithmetic sequence {an} based on the given
information.
A)
B)
C)
D)
information.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
73
Find the number of terms of the finite arithmetic sequence.
A) 58
B) 59
C) 60
D) 57
A) 58
B) 59
C) 60
D) 57

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
74
Find the sum.
Find the sum of the first 36 terms of the sequence.
A) 4,572
B) 9,144
C) 4,446
D) 9,108
Find the sum of the first 36 terms of the sequence.
A) 4,572
B) 9,144
C) 4,446
D) 9,108

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
75
From the given terms of the arithmetic sequence, find a1 and d.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
76
Find the indicated term of the arithmetic sequence based on the given information.
and Find
A) 13
B) 19
C) 25
D) 15
and Find
A) 13
B) 19
C) 25
D) 15

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
77
Find the indicated term of the arithmetic sequence based on the given information.
; Find .
A) 113
B) 104
C) 110
D) 107
; Find .
A) 113
B) 104
C) 110
D) 107

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
78
Find the sum.
A)
В)
C)
D) 387
A)
В)
C)
D) 387

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
79
Find the indicated term of the arithmetic sequence based on the given information.
and Find
A)
В)
C)
D)
and Find
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck
80
Find the indicated term.
Find
A) 133
B) 182
C)
D) 142
Find
A) 133
B) 182
C)
D) 142

Unlock Deck
Unlock for access to all 270 flashcards in this deck.
Unlock Deck
k this deck


