Deck 5: Systems of Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/215
Play
Full screen (f)
Deck 5: Systems of Equations and Inequalities
1
Solve the system of equations by using the addition method.


C
2
Solve the system of equations by using the substitution method.


C
3
Choose the one alternative that best completes the statement or answers the question.
Determine whether the ordered pair is a solution of the system.
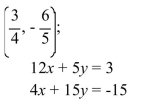
A) Yes
B) No
Determine whether the ordered pair is a solution of the system.
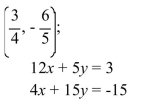
A) Yes
B) No
A
4
A system of linear equations in two variables may have infinitely many solutions. In such a case, the
equations are said to be .
equations are said to be .

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the system by substitution.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
6
Choose the one alternative that best completes the statement or answers the question.
Determine whether the ordered pair is a solution of the system.
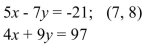
A) No
B) Yes
Determine whether the ordered pair is a solution of the system.
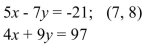
A) No
B) Yes

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system of equations by using the substitution method.
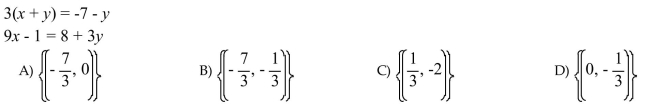
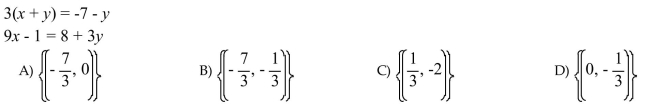

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the system of equations by using the addition method.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
9
Determine which point is the solution to the given system.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
10
Choose the one alternative that best completes the statement or answers the question.
Determine whether the ordered pair is a solution of the system.
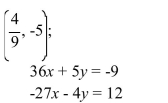
A) Yes
B) No
Determine whether the ordered pair is a solution of the system.
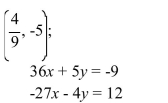
A) Yes
B) No

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system by substitution.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
12
Choose the one alternative that best completes the statement or answers the question.
Determine whether the ordered pair is a solution of the system.
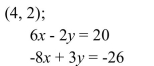
A) Yes
B) No
Determine whether the ordered pair is a solution of the system.
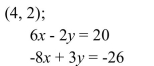
A) Yes
B) No

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system by substitution.
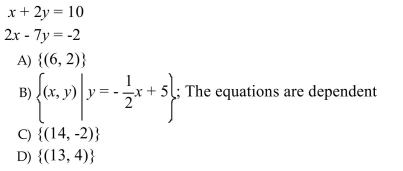
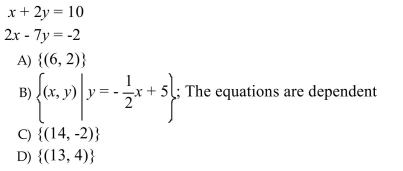

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
14
Two or more linear equations taken together is called a of linear equations.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system by substitution.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
16
A system of equations is given in which each question is written in slope-intercept form. Determine the
number of solutions. If the system does not have one unique solution, state whether the system is
inconsistent or whether the equations are dependent.
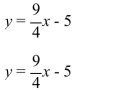
A) One solution
B) Infinitely many solutions; The equations are dependent.
C) No solution; The system is inconsistent.
number of solutions. If the system does not have one unique solution, state whether the system is
inconsistent or whether the equations are dependent.
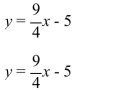
A) One solution
B) Infinitely many solutions; The equations are dependent.
C) No solution; The system is inconsistent.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
17
A system of equations that has no solution is called an system.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
18
A system of linear equations in two variables may have no solution. In such a case, the equations
represent lines.
represent lines.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
19
Two algebraic methods to solve a system of linear equations in two variables are the
method and the method.
method and the method.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
20
A to a system of equations in two variables is an ordered pair that is a solution to
each individual equation in the system.
each individual equation in the system.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.
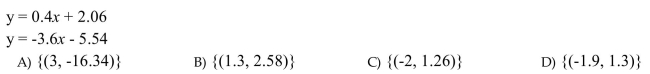
system is inconsistent or whether the equations are dependent.
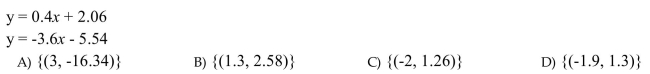

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the system of equations by using the addition method.
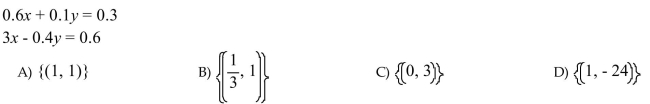
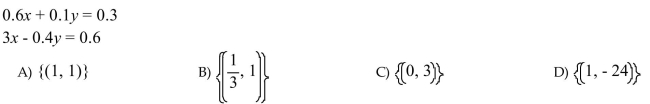

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the problem.
A fishing boat travels 36 mi with the current in 2 hr. It travels 42 mi against the current in 3 hr. Find the speed of the boat in still water.
A) The boat travels 2 mph in still water.
B) The boat travels 14 mph in still water.
C) The boat travels 18 mph in still water.
D) The boat travels 16 mph in still water.
A fishing boat travels 36 mi with the current in 2 hr. It travels 42 mi against the current in 3 hr. Find the speed of the boat in still water.
A) The boat travels 2 mph in still water.
B) The boat travels 14 mph in still water.
C) The boat travels 18 mph in still water.
D) The boat travels 16 mph in still water.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.
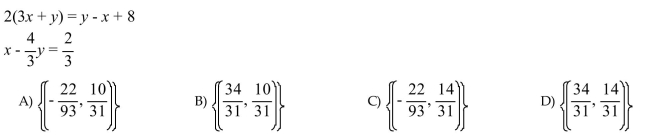
system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the problem.
The average weekly salary of two employees is $1,200. One makes $200 more than the other. Find their salaries.
A) One makes $700 and the other makes $900.
B) One makes $500 and the other makes $700.
C) One makes $1,100 and the other makes $1,300.
D) One makes $1,300 and the other makes $1,500.
The average weekly salary of two employees is $1,200. One makes $200 more than the other. Find their salaries.
A) One makes $700 and the other makes $900.
B) One makes $500 and the other makes $700.
C) One makes $1,100 and the other makes $1,300.
D) One makes $1,300 and the other makes $1,500.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the problem.
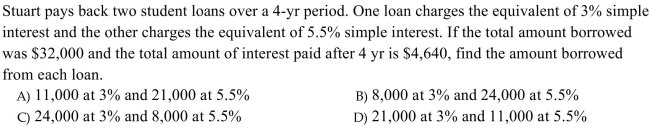
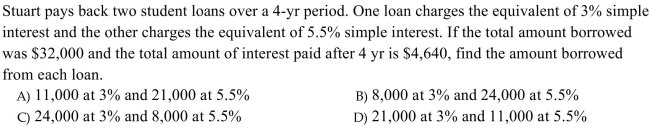

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.
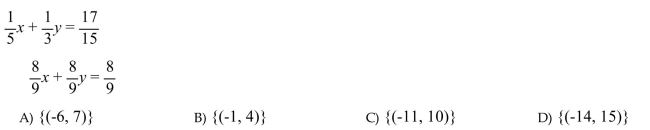
system is inconsistent or whether the equations are dependent.
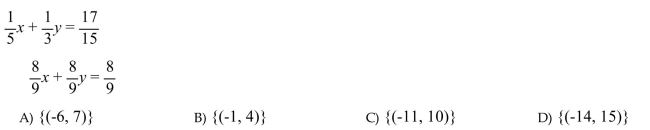

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the system of equations by using the addition method.
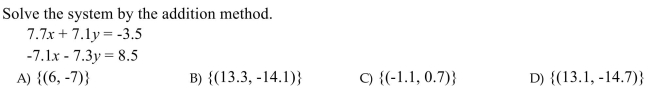
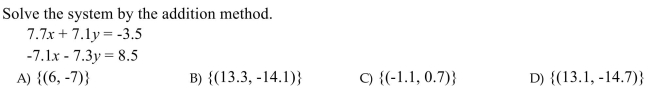

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the problem.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.
Camille and Sasha each make an ice cream sundae. Camille gets 2 scoops of Cherry ice cream and 1 scoop of Mint Chocolate Chunk ice cream for a total of 46 g of fat. Sasha has 3 scoops of Cherry ice
Cream and 2 scoop of Mint Chocolate Chunk ice cream for a total of 77 g of fat. How many grams
Of fat does 1 scoop of each type of ice cream have?
A) Cherry has 17 g of fat and Mint Chocolate Chunk has 14 g of fat.
B) Cherry has 14 g of fat and Mint Chocolate Chunk has 17 g of fat.
C) Cherry has 15 g of fat and Mint Chocolate Chunk has 16 g of fat.
D) Cherry has 16 g of fat and Mint Chocolate Chunk has 15 g of fat.
Camille and Sasha each make an ice cream sundae. Camille gets 2 scoops of Cherry ice cream and 1 scoop of Mint Chocolate Chunk ice cream for a total of 46 g of fat. Sasha has 3 scoops of Cherry ice
Cream and 2 scoop of Mint Chocolate Chunk ice cream for a total of 77 g of fat. How many grams
Of fat does 1 scoop of each type of ice cream have?
A) Cherry has 17 g of fat and Mint Chocolate Chunk has 14 g of fat.
B) Cherry has 14 g of fat and Mint Chocolate Chunk has 17 g of fat.
C) Cherry has 15 g of fat and Mint Chocolate Chunk has 16 g of fat.
D) Cherry has 16 g of fat and Mint Chocolate Chunk has 15 g of fat.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.
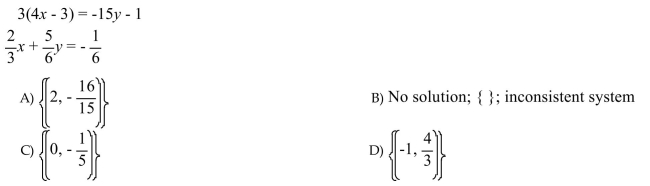
system is inconsistent or whether the equations are dependent.
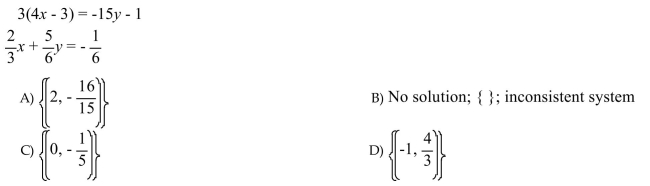

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
In an open market, the price of an item is dependent on the demand by consumers and the supply offered by producers. Competition between buyers and sellers steers the price toward an equilibrium price--that is,
The price where supply equals demand. The number of items offered and sold at the equilibrium price is the
Equilibrium quantity.
In an open market, the price of an item is dependent on the demand by consumers and the supply offered by producers. Competition between buyers and sellers steers the price toward an equilibrium price--that is,
The price where supply equals demand. The number of items offered and sold at the equilibrium price is the
Equilibrium quantity.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the system by using any method. If a system does not have one unique solution, state whether the
system is inconsistent or whether the equations are dependent.

system is inconsistent or whether the equations are dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
41
Find the measure of angles x and y.
(The figure is not necessarily drawn to scale.)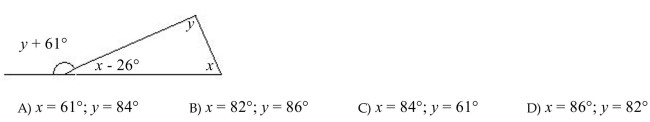
(The figure is not necessarily drawn to scale.)
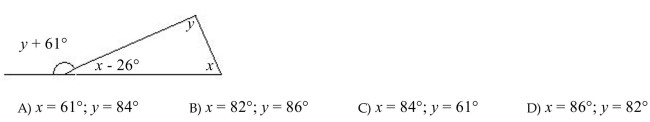

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem.
Nail polish remover is essentially a mixture of water and a chemical called acetone. How much pure acetone must be combined with a solution that is 28% acetone to make 24 oz of a 58% solution?
A) 14 oz
B) 12 oz
C) 10 oz
D) 17 oz
Nail polish remover is essentially a mixture of water and a chemical called acetone. How much pure acetone must be combined with a solution that is 28% acetone to make 24 oz of a 58% solution?
A) 14 oz
B) 12 oz
C) 10 oz
D) 17 oz

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
Find the area of the triangle bounded by the lines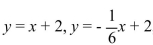 , and the x-axis.
, and the x-axis.
A) 4 square units
B) 2 square units
C) 28 square units
D) 14 square units
Find the area of the triangle bounded by the lines
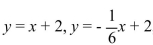 , and the x-axis.
, and the x-axis.A) 4 square units
B) 2 square units
C) 28 square units
D) 14 square units

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
To reach a sales meeting, Carrie traveled by plane for 2 hours and by car for an additional 2 hours. The plane travels 54 mph faster than the car. If the total distance traveled is 308 miles, what are the
Speeds of the plane and the car? (Assume that the plane and the car travel at constant rates.)
A) plane: 109 mph; car: 45 mph
B) plane: 104 mph; car: 50 mph
C) plane: 99 mph; car: 55 mph
D) plane: 94 mph; car: 40 mph
To reach a sales meeting, Carrie traveled by plane for 2 hours and by car for an additional 2 hours. The plane travels 54 mph faster than the car. If the total distance traveled is 308 miles, what are the
Speeds of the plane and the car? (Assume that the plane and the car travel at constant rates.)
A) plane: 109 mph; car: 45 mph
B) plane: 104 mph; car: 50 mph
C) plane: 99 mph; car: 55 mph
D) plane: 94 mph; car: 40 mph

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
46
Determine if the ordered triple is a solution to the system of equations.
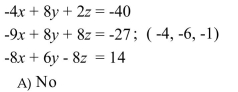
B) Yes
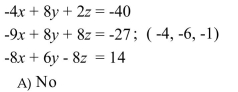
B) Yes

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
47
Use the substitution 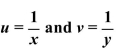 to rewrite the equations in the system in terms of the variables u and
to rewrite the equations in the system in terms of the variables u and
v. Solve the system in terms of u and v. Then back substitute to determine the solution set to the original
system in terms of x and y.
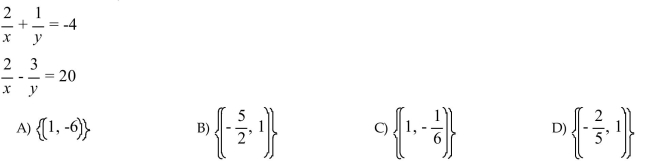
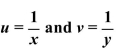 to rewrite the equations in the system in terms of the variables u and
to rewrite the equations in the system in terms of the variables u andv. Solve the system in terms of u and v. Then back substitute to determine the solution set to the original
system in terms of x and y.
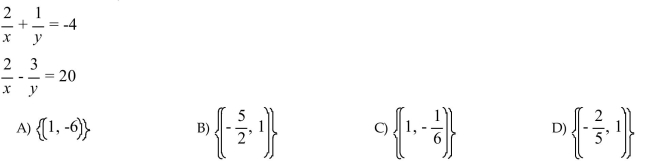

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
48
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
An equation of the form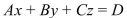 (where A, B, and C are not all zero) is called a
(where A, B, and C are not all zero) is called a
equation in three variables.
Provide the missing information.
An equation of the form
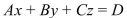 (where A, B, and C are not all zero) is called a
(where A, B, and C are not all zero) is called aequation in three variables.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
Two angles are supplementary. The measure of one angle is 68° more than 3 times the measure of the other angle. Find the measure of each angle.
A) 62° and 118°
B) 107° and 253°
C) 28° and 152°
D) 73° and 287°
Two angles are supplementary. The measure of one angle is 68° more than 3 times the measure of the other angle. Find the measure of each angle.
A) 62° and 118°
B) 107° and 253°
C) 28° and 152°
D) 73° and 287°

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
50
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
A solution to a system of linear equations in three variables is an ordered that satisfies
each equation in the system. Graphically, this is the point of of three planes.
Provide the missing information.
A solution to a system of linear equations in three variables is an ordered that satisfies
each equation in the system. Graphically, this is the point of of three planes.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.
A vendor at a carnival sells cotton candy and caramel apples for $2.00 each. The vendor is charged $60 to set up his booth. Furthermore, the vendor's average cost for each product he produces is
Approximately $0.80.
A) Write a linear cost function representing the cost C(x) (in $) to produce x products.
B) Write a linear revenue function representing the revenue R(x) (in $) for selling x products.
C) Determine the number of products to be produced and sold for the vendor to break even.
A vendor at a carnival sells cotton candy and caramel apples for $2.00 each. The vendor is charged $60 to set up his booth. Furthermore, the vendor's average cost for each product he produces is
Approximately $0.80.
A) Write a linear cost function representing the cost C(x) (in $) to produce x products.
B) Write a linear revenue function representing the revenue R(x) (in $) for selling x products.
C) Determine the number of products to be produced and sold for the vendor to break even.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the system by substitution.
9x - 5y = 16 y = - 12 x + 6
A) 2023, 12823
B) { }
C) {(-4, -4)}
D) {(4, 4)}
9x - 5y = 16 y = - 12 x + 6
A) 2023, 12823
B) { }
C) {(-4, -4)}
D) {(4, 4)}

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
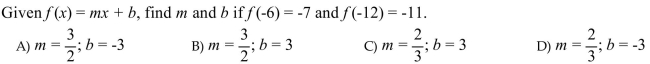
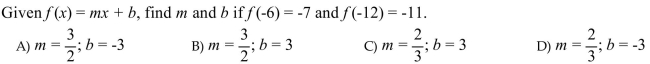

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the problem.
A helicopter flies 168 miles against the wind in 2 hours; with the wind, it can fly 252 miles in the same amount of time. Find the speed of the helicopter in still air.
A) 21 miles per hour
B) 63 miles per hour
C) 105 miles per hour
D) 84 miles per hour
A helicopter flies 168 miles against the wind in 2 hours; with the wind, it can fly 252 miles in the same amount of time. Find the speed of the helicopter in still air.
A) 21 miles per hour
B) 63 miles per hour
C) 105 miles per hour
D) 84 miles per hour

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.
The points shown in the graph represent the per capita consumption of chicken and beef in a country x years after the year 2000.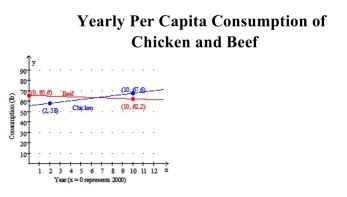 a. Use the given data points to write a linear function that approximates per capita consumption of
a. Use the given data points to write a linear function that approximates per capita consumption of
Chicken C(x) (in lb) at a time x years since the year 2000.
B) Use the given data points to write a linear function that approximates per capita consumption of
Beef B(x) (in lb) at a time x years since the year 2000.
C) Approximate the solution to the system of linear equations defined by the functions from parts (a)
And (b). Round to 1 decimal place. Interpret the meaning of the solution to the system.
The points shown in the graph represent the per capita consumption of chicken and beef in a country x years after the year 2000.
 a. Use the given data points to write a linear function that approximates per capita consumption of
a. Use the given data points to write a linear function that approximates per capita consumption ofChicken C(x) (in lb) at a time x years since the year 2000.
B) Use the given data points to write a linear function that approximates per capita consumption of
Beef B(x) (in lb) at a time x years since the year 2000.
C) Approximate the solution to the system of linear equations defined by the functions from parts (a)
And (b). Round to 1 decimal place. Interpret the meaning of the solution to the system.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
56
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
A solution to a linear equation in three variables is an ordered (x, y, z) that satisfies
the equation.
Provide the missing information.
A solution to a linear equation in three variables is an ordered (x, y, z) that satisfies
the equation.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the problem.
Abram and Fred leave opposite ends of a bike trail 8.5 miles apart and travel toward each other. Abram is traveling 3 mph faster than Fred. Find each of their speeds if they meet after 30 minutes.
A) Abram: 17 mph; Fred: 20 mph
B) Abram: 10 mph; Fred: 7 mph
C) Abram: 7 mph; Fred: 10 mph
D) Abram: 20 mph; Fred: 17 mph
Abram and Fred leave opposite ends of a bike trail 8.5 miles apart and travel toward each other. Abram is traveling 3 mph faster than Fred. Find each of their speeds if they meet after 30 minutes.
A) Abram: 17 mph; Fred: 20 mph
B) Abram: 10 mph; Fred: 7 mph
C) Abram: 7 mph; Fred: 10 mph
D) Abram: 20 mph; Fred: 17 mph

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
58
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
The graph of a linear equation in two variables is a line in a two-dimensional coordinate system.
The graph of a linear equation in three variables is a in a three-dimensional
coordinate system.
Provide the missing information.
The graph of a linear equation in two variables is a line in a two-dimensional coordinate system.
The graph of a linear equation in three variables is a in a three-dimensional
coordinate system.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
One angle measures 27° more than 2 times another. If the two angles are complementary, find the measures of the angles.
A) 26°; 64°
B) 23°; 67°
C) 21°; 69°
D) 31°; 59°
One angle measures 27° more than 2 times another. If the two angles are complementary, find the measures of the angles.
A) 26°; 64°
B) 23°; 67°
C) 21°; 69°
D) 31°; 59°

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
60
Choose the one alternative that best completes the statement or answers the question.
Find three ordered triples that are solutions to the linear equation in three variables.

Find three ordered triples that are solutions to the linear equation in three variables.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
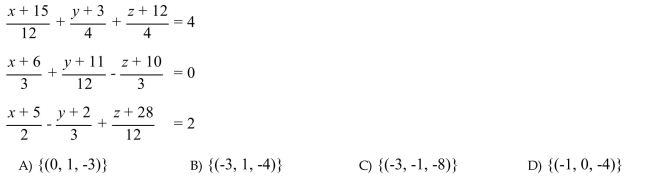
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
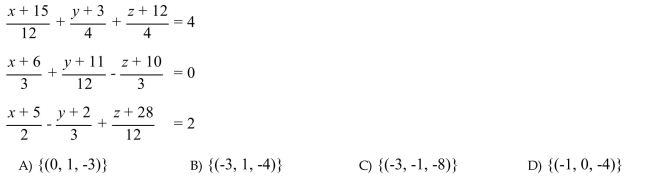

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
A theater charges $50 per ticket for seats in section A, $40 per ticket for seats in section B, and $20 per ticket for seats in section C. For one play, 9,500 tickets were sold for a total of $335,000 in
Revenue. If 500 more tickets in section B were sold than the other two sections combined, how many
Tickets in each section were sold?
A) 3,000 tickets in section A, 5,000 tickets in section B, and 1,500 tickets in section C were sold.
B) 3,000 tickets in section A, 3,500 tickets in section B, and 1,500 tickets in section C were sold.
C) 1,500 tickets in section A, 3,500 tickets in section B, and 3,000 tickets in section C were sold.
D) 1,500 tickets in section A, 5,000 tickets in section B, and 3,000 tickets in section C were sold.
A theater charges $50 per ticket for seats in section A, $40 per ticket for seats in section B, and $20 per ticket for seats in section C. For one play, 9,500 tickets were sold for a total of $335,000 in
Revenue. If 500 more tickets in section B were sold than the other two sections combined, how many
Tickets in each section were sold?
A) 3,000 tickets in section A, 5,000 tickets in section B, and 1,500 tickets in section C were sold.
B) 3,000 tickets in section A, 3,500 tickets in section B, and 1,500 tickets in section C were sold.
C) 1,500 tickets in section A, 3,500 tickets in section B, and 3,000 tickets in section C were sold.
D) 1,500 tickets in section A, 5,000 tickets in section B, and 3,000 tickets in section C were sold.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
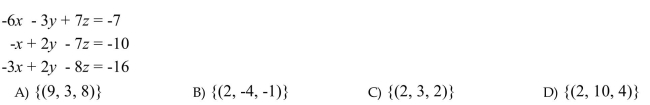
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
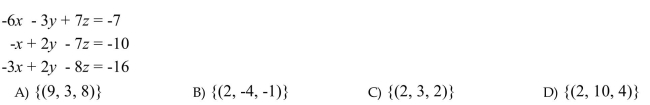

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the problem.
A basketball player scored 33 points in one game. In basketball, some baskets are worth 3 points, some are worth 2 points, and free-throws are worth 1 point. He scored four more 2-point baskets
Than he did 3-point baskets. The number of free throws equaled the sum of the number of 2-point
And 3-point shots made. How many free-throws did he make?
A) He made 3 free-throws.
B) He made 7 free-throws.
C) He made 13 free-throws.
D) He made 10 free-throws.
A basketball player scored 33 points in one game. In basketball, some baskets are worth 3 points, some are worth 2 points, and free-throws are worth 1 point. He scored four more 2-point baskets
Than he did 3-point baskets. The number of free throws equaled the sum of the number of 2-point
And 3-point shots made. How many free-throws did he make?
A) He made 3 free-throws.
B) He made 7 free-throws.
C) He made 13 free-throws.
D) He made 10 free-throws.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
71
Identify the ordered triple that is a solution to the system.
-2x - 4y - 6z = 16
-8x - 7y + 7z = -2 4x - 3y - 7z = -8
A) (-5, 9, -7)
B) (-11, 3, -1)
C) (-5, 3, -3)
D) All three points are solutions to the system.
-2x - 4y - 6z = 16
-8x - 7y + 7z = -2 4x - 3y - 7z = -8
A) (-5, 9, -7)
B) (-11, 3, -1)
C) (-5, 3, -3)
D) All three points are solutions to the system.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
72
Identify the system for which the ordered triple is a solution.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
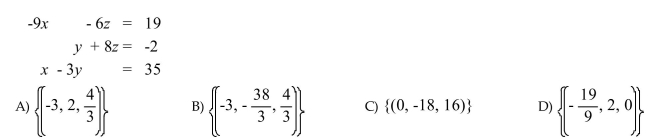
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
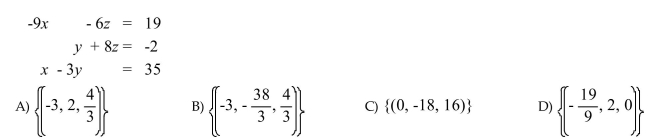

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
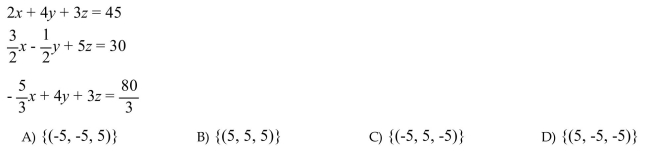
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
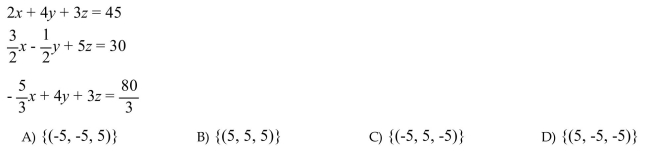

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
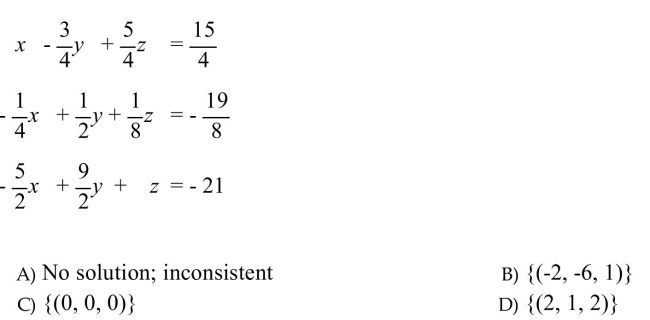
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
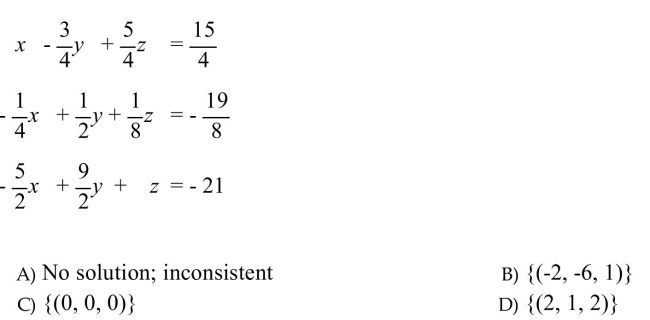

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
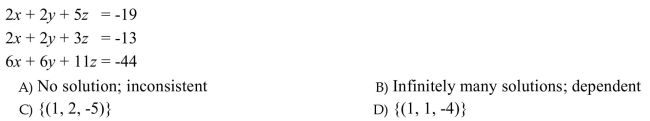
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.
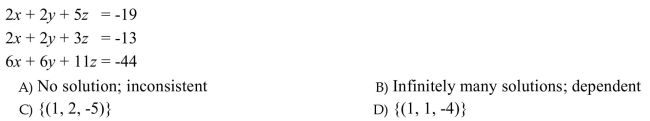

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the problem.
Josie invested $13,000 in three different mutual funds. A fund containing large cap stocks made 5.7% return in 1 yr. A real estate fund lost 12.6% in 1 yr, and a bond fund made 3.5% in 1 yr. The
Amount invested in the large cap stock fund was twice the amount invested in the real estate fund. If
Josie had a net return of $162.50 across all investments, how much did she invest in the large cap
Fund?
A) She invested $8,000 in the large cap fund.
B) She invested $5,000 in the large cap fund.
C) She invested $5,500 in the large cap fund.
D) She invested $2,500 in the large cap fund.
Josie invested $13,000 in three different mutual funds. A fund containing large cap stocks made 5.7% return in 1 yr. A real estate fund lost 12.6% in 1 yr, and a bond fund made 3.5% in 1 yr. The
Amount invested in the large cap stock fund was twice the amount invested in the real estate fund. If
Josie had a net return of $162.50 across all investments, how much did she invest in the large cap
Fund?
A) She invested $8,000 in the large cap fund.
B) She invested $5,000 in the large cap fund.
C) She invested $5,500 in the large cap fund.
D) She invested $2,500 in the large cap fund.

Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the
number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.

number of solutions to the system, and determine whether the system is inconsistent, or the equations are
dependent.


Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the system. If there is more than one solution, write the general solution.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the system. If there is more than one solution, write the general solution.



Unlock Deck
Unlock for access to all 215 flashcards in this deck.
Unlock Deck
k this deck


