Deck 14: Voting and Apportionment
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/71
Play
Full screen (f)
Deck 14: Voting and Apportionment
1
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
A second election is then held resulting in the following preference table:
If the plurality with elimination method is used to determine the winner, is the montonicity
Criterion satisfied?
A) Yes
B) No
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

A second election is then held resulting in the following preference table:

If the plurality with elimination method is used to determine the winner, is the montonicity
Criterion satisfied?
A) Yes
B) No
A
2
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table: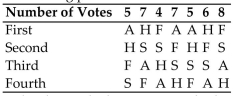
If the plurality with elimination method is used to determine the winner, is the head-to-head
Criterion satisfied?
A) Yes
B) No
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table:

If the plurality with elimination method is used to determine the winner, is the head-to-head
Criterion satisfied?
A) Yes
B) No
A
3
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
If the Borda count method is used to determine the winner, is the head-to-head criterion satisfied?
A) Yes
B) No
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

If the Borda count method is used to determine the winner, is the head-to-head criterion satisfied?
A) Yes
B) No
A
4
Make a preference table for the given voting situation.
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
Determine the winner using the Borda count method and if the winner received a majority of first
Place votes.
A) Jones; No
B) Smith; Yes
C) Jones; Yes
D) Smith; No
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

Determine the winner using the Borda count method and if the winner received a majority of first
Place votes.
A) Jones; No
B) Smith; Yes
C) Jones; Yes
D) Smith; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
5
Make a preference table for the given voting situation.
-Ten voters are asked to rank 4 brands of cell phones: A, B, C, and D. The ten voters turn in the Following ballots showing their preferences in order:
Make a preference table for these ballots.
A)
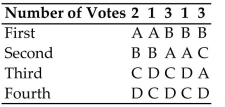
B)
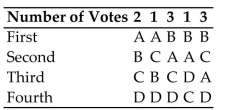
C)

D)
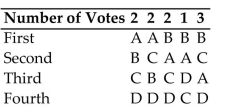
-Ten voters are asked to rank 4 brands of cell phones: A, B, C, and D. The ten voters turn in the Following ballots showing their preferences in order:
Make a preference table for these ballots.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
6
An order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul.
A condominium association is holding an election for president of the board of directors. Each
Member ranks the candidates from first to third. The preference table below shows the results of
The ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).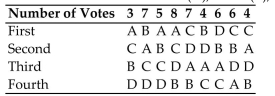
Determine the winner using the Borda count method and if the winner received a majority of first
Place votes.
A) Cleary; No
B) Abbott; No
C) Blake; No
D) Downs; No
A condominium association is holding an election for president of the board of directors. Each
Member ranks the candidates from first to third. The preference table below shows the results of
The ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).

Determine the winner using the Borda count method and if the winner received a majority of first
Place votes.
A) Cleary; No
B) Abbott; No
C) Blake; No
D) Downs; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
7
Make a preference table for the given voting situation.
Eight voters are asked to rank 4 brands of ice cream: A, B, C, and D. The eight voters turn in the
Following ballots showing their preferences in order:
Eight voters are asked to rank 4 brands of ice cream: A, B, C, and D. The eight voters turn in the
Following ballots showing their preferences in order:


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
8
Make a preference table for the given voting situation.
-Eight voters are asked to rank 3 brands of automobiles: A, B, and C. The eight voters turn in the Following ballots showing their preferences in order:
Make a preference table for these ballots.
A)
B)

C)

D)

-Eight voters are asked to rank 3 brands of automobiles: A, B, and C. The eight voters turn in the Following ballots showing their preferences in order:
Make a preference table for these ballots.
A)
B)

C)

D)


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
9
Make a preference table for the given voting situation.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.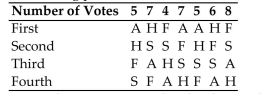
Determine the winner using the plurality method and if the winner received a majority of first
Place votes.
A) Alaska; Yes
B) Hawaii; Yes
C) Hawaii; No
D) Alaska; No
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.

Determine the winner using the plurality method and if the winner received a majority of first
Place votes.
A) Alaska; Yes
B) Hawaii; Yes
C) Hawaii; No
D) Alaska; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
10
An order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.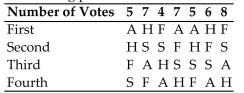
Determine the winner using the plurality with elimination method and if the winner received a
Majority of first place votes.
A) Alaska; Yes
B) Hawaii; Yes
C) Hawaii; No
D) Alaska; No
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.

Determine the winner using the plurality with elimination method and if the winner received a
Majority of first place votes.
A) Alaska; Yes
B) Hawaii; Yes
C) Hawaii; No
D) Alaska; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
11
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
If the Borda count method is used to determine the winner, is the majority criterion satisfied?
A) Yes
B) No
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

If the Borda count method is used to determine the winner, is the majority criterion satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
12
An order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul.
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
Determine the winner using the pairwise comparison method and if the winner received a
Majority of first place votes.
A) Smith; Yes
B) Jones; Yes
C) Smith; No
D) Jones; No
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

Determine the winner using the pairwise comparison method and if the winner received a
Majority of first place votes.
A) Smith; Yes
B) Jones; Yes
C) Smith; No
D) Jones; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
13
Make a preference table for the given voting situation.
-Ten voters are asked to rank 3 brands of shoes: A, B, and C. The ten voters turn in the following Ballots showing their preferences in order:
Make a preference table for these ballots.
A)
B)

C)

D)

-Ten voters are asked to rank 3 brands of shoes: A, B, and C. The ten voters turn in the following Ballots showing their preferences in order:
Make a preference table for these ballots.
A)
B)

C)

D)


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
14
An order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.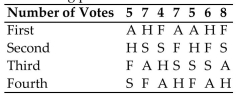
Determine the winner using the pairwise comparison method.
A) Florida & Hawaii (tie)
B) Alaska & Florida (tie)
C) Alaska
D) Alaska & Hawaii (tie)
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.

Determine the winner using the pairwise comparison method.
A) Florida & Hawaii (tie)
B) Alaska & Florida (tie)
C) Alaska
D) Alaska & Hawaii (tie)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
15
Make a preference table for the given voting situation.
A condominium association is holding an election for president of the board of directors. Each
Member ranks the candidates from first to third. The preference table below shows the results of
The ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).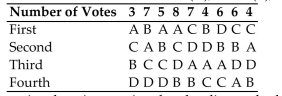
Determine the winner using the plurality method and if the winner received a majority of first
Place votes.
A) Cleary; Yes
B) Abbott; Yes
C) Abbott; No
D) Cleary; No
A condominium association is holding an election for president of the board of directors. Each
Member ranks the candidates from first to third. The preference table below shows the results of
The ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).

Determine the winner using the plurality method and if the winner received a majority of first
Place votes.
A) Cleary; Yes
B) Abbott; Yes
C) Abbott; No
D) Cleary; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
16
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table: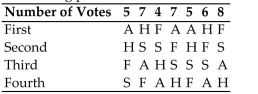
If the Borda count method is used to determine the winner, is the majority criterion satisfied?
A) Yes
B) No
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table:

If the Borda count method is used to determine the winner, is the majority criterion satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
17
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
If the plurality method is used to determine the winner, is the head-to-head criterion satisfied?
A) Yes
B) No
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

If the plurality method is used to determine the winner, is the head-to-head criterion satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
18
Make a preference table for the given voting situation.
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
Determine the winner using the plurality method and if the winner received a majority of first
Place votes.
A) Clark; No
B) Jones; No
C) Clark; Yes
D) Smith; Yes
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

Determine the winner using the plurality method and if the winner received a majority of first
Place votes.
A) Clark; No
B) Jones; No
C) Clark; Yes
D) Smith; Yes

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
19
An order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.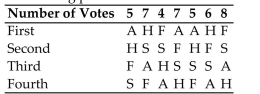
Determine the winner using the Borda count method and if the winner received a majority of first
Place votes.
A) San Antonio; No
B) Florida; No
C) Alaska; No
D) Hawaii; No
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table.

Determine the winner using the Borda count method and if the winner received a majority of first
Place votes.
A) San Antonio; No
B) Florida; No
C) Alaska; No
D) Hawaii; No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
20
An order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul.
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
Determine the winner using the plurality with elimination method and if the winner received a
Majority of first place votes.
A) Smith; No
B) Jones; Yes
C) Jones; No
D) Smith, Yes
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

Determine the winner using the plurality with elimination method and if the winner received a
Majority of first place votes.
A) Smith; No
B) Jones; Yes
C) Jones; No
D) Smith, Yes

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
21
Find the standard divisor for the given situation. Round your answer to two decimals.
A school district receives a grant to purchase 50 new computers to be apportioned among the 6
Schools in the district based on the student population of each school. The student populations are
Given in the following table.
Find the standard quota for school A.
A) 11.56
B) 12.62
C) 13.16
D) 10.01
A school district receives a grant to purchase 50 new computers to be apportioned among the 6
Schools in the district based on the student population of each school. The student populations are
Given in the following table.

Find the standard quota for school A.
A) 11.56
B) 12.62
C) 13.16
D) 10.01

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
22
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A),
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table: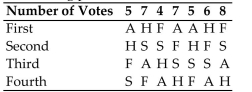
If the four voters who voted F, S, H, A, in that order, change their votes to H, S, A, F, and if the
Plurality with elimination method is used to determine the winner, is the monotonicity criterion
Satisfied?
A) Yes
B) No
Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according
To the following preference table:

If the four voters who voted F, S, H, A, in that order, change their votes to H, S, A, F, and if the
Plurality with elimination method is used to determine the winner, is the monotonicity criterion
Satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
23
Find the standard divisor for the given situation. Round your answer to two decimals.
A university has 25 scholarships to be apportioned among the engineering students based on the
Enrollment in each department. There are three departments - Mechanical Engineering (M),
Electrical Engineering (E), and Civil Engineering (C). The number of students in each department
Is given in the following table.
A) 27.32
B) 28.44
C) 31.88
D) 29.72
A university has 25 scholarships to be apportioned among the engineering students based on the
Enrollment in each department. There are three departments - Mechanical Engineering (M),
Electrical Engineering (E), and Civil Engineering (C). The number of students in each department
Is given in the following table.

A) 27.32
B) 28.44
C) 31.88
D) 29.72

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
24
Find the standard divisor for the given situation. Round your answer to two decimals.
The faculty senate of a university has 45 senators to be apportioned among its four colleges based
On the number of faculty in each college. The colleges are Liberal Arts (L), Sciences (S), Business
(B), and Engineering (E). The number of faculty in each college is shown in the following table.
A) 27.18
B) 21.76
C) 24.76
D) 30.42
The faculty senate of a university has 45 senators to be apportioned among its four colleges based
On the number of faculty in each college. The colleges are Liberal Arts (L), Sciences (S), Business
(B), and Engineering (E). The number of faculty in each college is shown in the following table.

A) 27.18
B) 21.76
C) 24.76
D) 30.42

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
25
Find the standard divisor for the given situation. Round your answer to two decimals.
A small country consists of seven states; there are 156 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Find the modified quota for state F using the divisor 92.
A) 27.29
B) 26.44
C) 27.93
D) 28.16
A small country consists of seven states; there are 156 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Find the modified quota for state F using the divisor 92.
A) 27.29
B) 26.44
C) 27.93
D) 28.16

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
26
Find the standard divisor for the given situation. Round your answer to two decimals.
The faculty senate of a university has 40 senators to be apportioned among its four colleges based
On the number of faculty in each college. The colleges are Liberal Arts (L), Sciences (S), Business
(B), and Engineering (E). The number of faculty in each college is shown in the following table.
Find the standard quota for the College of Sciences.
A) 11.61
B) 12.75
C) 14.5
D) 10.37
The faculty senate of a university has 40 senators to be apportioned among its four colleges based
On the number of faculty in each college. The colleges are Liberal Arts (L), Sciences (S), Business
(B), and Engineering (E). The number of faculty in each college is shown in the following table.

Find the standard quota for the College of Sciences.
A) 11.61
B) 12.75
C) 14.5
D) 10.37

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
27
A condominium association is holding an election for president of the board of directors. Each
Member ranks the candidates from first to third. The preference table below shows the results of
The ballots with candidates Abbott (A), Blake (B), Cleary (C), and Downs (D).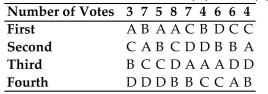
If the plurality method if used to determine the winner and Downs drops out, is the irrelevant
Alternatives criterion satisfied?
A) Yes
B) No
Member ranks the candidates from first to third. The preference table below shows the results of
The ballots with candidates Abbott (A), Blake (B), Cleary (C), and Downs (D).

If the plurality method if used to determine the winner and Downs drops out, is the irrelevant
Alternatives criterion satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
28
Find the standard divisor for the given situation. Round your answer to two decimals.
A small country consists of seven states; there are 158 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
A) 76.87
B) 84.65
C) 75.52
D) 92.77
A small country consists of seven states; there are 158 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

A) 76.87
B) 84.65
C) 75.52
D) 92.77

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
29
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
If the plurality method is used to determine the winner and Clark drops out, is the irrelevant
Alternatives criterion satisfied?
A) Yes
B) No
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

If the plurality method is used to determine the winner and Clark drops out, is the irrelevant
Alternatives criterion satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
30
Find the standard divisor for the given situation. Round your answer to two decimals.
A university has 22 scholarships to be apportioned among the engineering students based on the
Enrollment in each department. There are three departments - Mechanical Engineering (M),
Electrical Engineering (E), and Civil Engineering (C). The number of students in each department
Is given in the following table.
Find the standard quota for the Mechanical Engineering Department.
A) 6.9
B) 7.51
C) 7.21
D) 6.43
A university has 22 scholarships to be apportioned among the engineering students based on the
Enrollment in each department. There are three departments - Mechanical Engineering (M),
Electrical Engineering (E), and Civil Engineering (C). The number of students in each department
Is given in the following table.

Find the standard quota for the Mechanical Engineering Department.
A) 6.9
B) 7.51
C) 7.21
D) 6.43

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
31
Find the standard divisor for the given situation. Round your answer to two decimals.
A small country consists of seven states; there are 157 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Find the standard quota for state C.
A) 35.86
B) 31.99
C) 35.22
D) 29.19
A small country consists of seven states; there are 157 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Find the standard quota for state C.
A) 35.86
B) 31.99
C) 35.22
D) 29.19

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
32
Find the standard divisor for the given situation. Round your answer to two decimals.
A small city has 48 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.
A) 534.65
B) 566.5
C) 432.31
D) 636.98
A small city has 48 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.

A) 534.65
B) 566.5
C) 432.31
D) 636.98

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
33
Find the standard divisor for the given situation. Round your answer to two decimals.
A small country consists of 7 provinces with the following populations: There are 320 federal judges to be apportioned according to the population of each province.
There are 320 federal judges to be apportioned according to the population of each province.
Find the standard quota for province G.
A) 53.29
B) 58.14
C) 67.74
D) 45.54
A small country consists of 7 provinces with the following populations:
 There are 320 federal judges to be apportioned according to the population of each province.
There are 320 federal judges to be apportioned according to the population of each province.Find the standard quota for province G.
A) 53.29
B) 58.14
C) 67.74
D) 45.54

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
34
Find the standard divisor for the given situation. Round your answer to two decimals.
A school district receives a grant to purchase 66 new computers to be apportioned among the 6
Schools in the district based on the student population of each school. The student populations are
Given in the following table.
A) 18.08
B) 20.58
C) 18.85
D) 23.77
A school district receives a grant to purchase 66 new computers to be apportioned among the 6
Schools in the district based on the student population of each school. The student populations are
Given in the following table.

A) 18.08
B) 20.58
C) 18.85
D) 23.77

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
35
Find the standard divisor for the given situation. Round your answer to two decimals.
A school district receives a grant to purchase 55 new computers to be apportioned among the 6
Schools in the district based on the student population of each school. The student populations are
Given in the following table.
Find the modified quota for school B using the divisor 28.5.
A) 7.52
B) 7.55
C) 7.40
D) 7.63
A school district receives a grant to purchase 55 new computers to be apportioned among the 6
Schools in the district based on the student population of each school. The student populations are
Given in the following table.

Find the modified quota for school B using the divisor 28.5.
A) 7.52
B) 7.55
C) 7.40
D) 7.63

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
36
The Mathematics Department is holding an election for department chair. Each member ranks the
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
If the Borda count method is used to determine the winner and Clark drops out, is the irrelevant
Alternatives criterion satisfied?
A) Yes
B) No
Candidates from first to third. The preference table below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).

If the Borda count method is used to determine the winner and Clark drops out, is the irrelevant
Alternatives criterion satisfied?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
37
Find the standard divisor for the given situation. Round your answer to two decimals.
A small city has 46 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.
Find the modified quota for the Sixth Precinct using the divisor 513.
A) 7.98
B) 8.03
C) 7.79
D) 7.85
A small city has 46 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.

Find the modified quota for the Sixth Precinct using the divisor 513.
A) 7.98
B) 8.03
C) 7.79
D) 7.85

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
38
Find the standard divisor for the given situation. Round your answer to two decimals.
A small city has 45 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.
Find the standard quota for the Third Precinct.
A) 6.76
B) 4.59
C) 5.47
D) 5.16
A small city has 45 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.

Find the standard quota for the Third Precinct.
A) 6.76
B) 4.59
C) 5.47
D) 5.16

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
39
Find the standard divisor for the given situation. Round your answer to two decimals.
A university has 27 scholarships to be apportioned among the engineering students based on the
Enrollment in each department. There are three departments - Mechanical Engineering (M),
Electrical Engineering (E), and Civil Engineering (C). The number of students in each department
Is given in the following table.
Find the modified quota for the Civil Engineering Department using the divisor 27.
A) 5.67
B) 5.47
C) 5.52
D) 5.72
A university has 27 scholarships to be apportioned among the engineering students based on the
Enrollment in each department. There are three departments - Mechanical Engineering (M),
Electrical Engineering (E), and Civil Engineering (C). The number of students in each department
Is given in the following table.

Find the modified quota for the Civil Engineering Department using the divisor 27.
A) 5.67
B) 5.47
C) 5.52
D) 5.72

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
40
Find the standard divisor for the given situation. Round your answer to two decimals.
A small country consists of 7 provinces with the following populations: There are 200 federal judges to be apportioned according to the population of each province.
There are 200 federal judges to be apportioned according to the population of each province.
A) 960.59
B) 755.6
C) 880.38
D) 1123.98
A small country consists of 7 provinces with the following populations:
 There are 200 federal judges to be apportioned according to the population of each province.
There are 200 federal judges to be apportioned according to the population of each province.A) 960.59
B) 755.6
C) 880.38
D) 1123.98

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
41
Find the standard divisor for the given situation. Round your answer to two decimals.
A small country consists of 7 provinces with the following populations: There are 340 federal judges to be apportioned according to the population of each province.
There are 340 federal judges to be apportioned according to the population of each province.
Find the modified quota for province G using the divisor 600.
A) 52.28
B) 53.85
C) 51.97
D) 53.32
A small country consists of 7 provinces with the following populations:
 There are 340 federal judges to be apportioned according to the population of each province.
There are 340 federal judges to be apportioned according to the population of each province.Find the modified quota for province G using the divisor 600.
A) 52.28
B) 53.85
C) 51.97
D) 53.32

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the specified paradox occurs.
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Does the Alabama paradox occur using Hamiltonʹs method if the number of seats is increased
From 160 to 161?
A) Yes
B) No
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Does the Alabama paradox occur using Hamiltonʹs method if the number of seats is increased
From 160 to 161?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
43
Find the apportionment asked for.
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Find the apportionment for state D using Jeffersonʹs method.
A) 26
B) 23
C) 25
D) 24
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Find the apportionment for state D using Jeffersonʹs method.
A) 26
B) 23
C) 25
D) 24

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
44
Find the apportionment asked for.
A small country consists of 7 provinces with the following populations: There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. Find
The apportionment for province G using Adamsʹ method.
A) 54
B) 55
C) 53
D) 56
A small country consists of 7 provinces with the following populations:
 There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. FindThe apportionment for province G using Adamsʹ method.
A) 54
B) 55
C) 53
D) 56

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
45
Find the apportionment asked for.
A small city has 50 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.
Find the apportionment for the Seventh Precinct using Websterʹs method.
A) 6
B) 7
C) 5
D) 4
A small city has 50 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.

Find the apportionment for the Seventh Precinct using Websterʹs method.
A) 6
B) 7
C) 5
D) 4

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
46
Determine whether the specified paradox occurs.
In a small country consisting of 5 provinces, 300 federal judges are apportioned according to the
Population of each province. The population of each province is shown for the years 1995 and
2000.
Does the population paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No
In a small country consisting of 5 provinces, 300 federal judges are apportioned according to the
Population of each province. The population of each province is shown for the years 1995 and
2000.

Does the population paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
47
Find the standard divisor for the given situation. Round your answer to two decimals.
The faculty senate of a university has 60 senators to be apportioned among its four colleges based
On the number of faculty in each college. The colleges are Liberal Arts (L), Sciences (S), Business
(B), and Engineering (E). The number of faculty in each college is shown in the following table.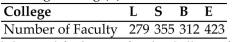
Find the modified quota for the College of Engineering using the divisor 27.
A) 15.27
B) 15.11
C) 15.43
D) 15.67
The faculty senate of a university has 60 senators to be apportioned among its four colleges based
On the number of faculty in each college. The colleges are Liberal Arts (L), Sciences (S), Business
(B), and Engineering (E). The number of faculty in each college is shown in the following table.
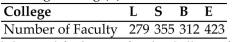
Find the modified quota for the College of Engineering using the divisor 27.
A) 15.27
B) 15.11
C) 15.43
D) 15.67

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
48
Find the apportionment asked for.
A small city has 50 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.
Find the apportionment for the Seventh Precinct using Adamsʹ method.
A) 5
B) 4
C) 7
D) 6
A small city has 50 police officers to be apportioned among 8 precincts based on the population of
Each precinct. The populations are given in the following table.

Find the apportionment for the Seventh Precinct using Adamsʹ method.
A) 5
B) 4
C) 7
D) 6

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
49
Determine whether the specified paradox occurs.
A country with two states has 16 seats in the legislature. The population of each state is given by: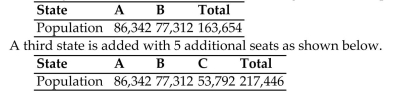 Does the new-states paradox occur using Hamiltonʹs method of apportionment?
Does the new-states paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No
A country with two states has 16 seats in the legislature. The population of each state is given by:
 Does the new-states paradox occur using Hamiltonʹs method of apportionment?
Does the new-states paradox occur using Hamiltonʹs method of apportionment?A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
50
Determine whether the specified paradox occurs.
A city has 204 police officers to be apportioned among 4 precincts based on the population of each
Precinct. The populations are given in the following table.
Does the Alabama paradox occur using Hamiltonʹs method if the number of police officers is
Increased from 204 to 205?
A) Yes
B) No
A city has 204 police officers to be apportioned among 4 precincts based on the population of each
Precinct. The populations are given in the following table.

Does the Alabama paradox occur using Hamiltonʹs method if the number of police officers is
Increased from 204 to 205?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the specified paradox occurs.
A small country consists of 7 provinces with the following populations: There are 300 federal judges to be apportioned according to the population of each province. Does
There are 300 federal judges to be apportioned according to the population of each province. Does
The Alabama paradox occur using Hamiltonʹs method if the number of judges is increased from
300 to 301?
A) Yes
B) No
A small country consists of 7 provinces with the following populations:
 There are 300 federal judges to be apportioned according to the population of each province. Does
There are 300 federal judges to be apportioned according to the population of each province. DoesThe Alabama paradox occur using Hamiltonʹs method if the number of judges is increased from
300 to 301?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
52
Find the apportionment asked for.
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Find the apportionment for state D using Adamsʹ method.
A) 24
B) 26
C) 25
D) 23
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Find the apportionment for state D using Adamsʹ method.
A) 24
B) 26
C) 25
D) 23

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
53
Find the apportionment asked for.
A small country consists of 7 provinces with the following populations: There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. Find
The apportionment for province G using Jeffersonʹs method.
A) 55
B) 56
C) 54
D) 53
A small country consists of 7 provinces with the following populations:
 There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. FindThe apportionment for province G using Jeffersonʹs method.
A) 55
B) 56
C) 54
D) 53

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
54
Find the apportionment asked for.
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Find the apportionment for state D using Hamiltonʹs method.
A) 25
B) 26
C) 23
D) 24
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Find the apportionment for state D using Hamiltonʹs method.
A) 25
B) 26
C) 23
D) 24

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
55
Determine whether the specified paradox occurs.
A town has 13 police officers to be apportioned among 3 precincts based on the population of each
Precinct. The populations for the years 1998 and 1999 are given in the following table.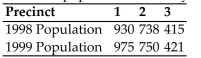
Does the population paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No
A town has 13 police officers to be apportioned among 3 precincts based on the population of each
Precinct. The populations for the years 1998 and 1999 are given in the following table.

Does the population paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
56
Find the apportionment asked for.
A small country consists of 7 provinces with the following populations: There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. Find
The apportionment for province G using Hamiltonʹs method.
A) 56
B) 54
C) 55
D) 53
A small country consists of 7 provinces with the following populations:
 There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. FindThe apportionment for province G using Hamiltonʹs method.
A) 56
B) 54
C) 55
D) 53

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
57
Determine whether the specified paradox occurs.
A country with two states has 16 seats in the legislature. The population of each state (in
Thousands) is given by:
Does the new-states paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No
A country with two states has 16 seats in the legislature. The population of each state (in
Thousands) is given by:

Does the new-states paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
58
Determine whether the specified paradox occurs.
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown below for the years
1990 and 1995.
Does the population paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown below for the years
1990 and 1995.

Does the population paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
59
Find the apportionment asked for.
A small country consists of 7 provinces with the following populations: There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. Find
The apportionment for province G using Websterʹs method.
A) 56
B) 53
C) 54
D) 55
A small country consists of 7 provinces with the following populations:
 There are 300 federal judges to be apportioned according to the population of each province. Find
There are 300 federal judges to be apportioned according to the population of each province. FindThe apportionment for province G using Websterʹs method.
A) 56
B) 53
C) 54
D) 55

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
60
Find the apportionment asked for.
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.
Find the apportionment for state D using Websterʹs method.
A) 23
B) 24
C) 25
D) 26
A small country consists of seven states; there are 160 seats in the legislature that need to be
Apportioned among the seven states; and the population of each state is shown in the table.

Find the apportionment for state D using Websterʹs method.
A) 23
B) 24
C) 25
D) 26

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
Which voting method may violate the majority criterion?
A) plurality
B) plurality with elimination
C) Borda count
D) pairwise comparison
Which voting method may violate the majority criterion?
A) plurality
B) plurality with elimination
C) Borda count
D) pairwise comparison

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.
Which fairness criterion is always satisfied by the plurality with elimination method?
A) monotonicity criterion
B) majority criterion
C) irrelevant alternatives criterion
D) head-to-head criterion
Which fairness criterion is always satisfied by the plurality with elimination method?
A) monotonicity criterion
B) majority criterion
C) irrelevant alternatives criterion
D) head-to-head criterion

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the problem.
Which apportionment paradox may be produced by the Adamsʹ method but not the Webster
Method?
A) Alabama
B) population
C) new-states
D) none of these
Which apportionment paradox may be produced by the Adamsʹ method but not the Webster
Method?
A) Alabama
B) population
C) new-states
D) none of these

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
Which apportionment method may produce the new-states paradox?
A) Webster
B) Jefferson
C) Hamilton
D) Adams
Which apportionment method may produce the new-states paradox?
A) Webster
B) Jefferson
C) Hamilton
D) Adams

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
Which apportionment method never violates the quota rule?
A) Adams
B) Webster
C) Jefferson
D) Hamilton
Which apportionment method never violates the quota rule?
A) Adams
B) Webster
C) Jefferson
D) Hamilton

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
Which apportionment method may produce the Alabama paradox?
A) Webster
B) Jefferson
C) Hamilton
D) Adams
Which apportionment method may produce the Alabama paradox?
A) Webster
B) Jefferson
C) Hamilton
D) Adams

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the problem.
Which apportionment method may produce the population paradox?
A) Jefferson
B) Webster
C) Adams
D) Hamilton
Which apportionment method may produce the population paradox?
A) Jefferson
B) Webster
C) Adams
D) Hamilton

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
68
Determine whether the specified paradox occurs.
A country with two states has 75 seats in the legislature. The population of each state (in
Thousands) is given by: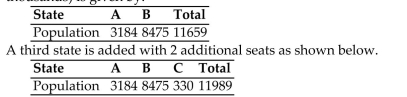
Does the new-states paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No
A country with two states has 75 seats in the legislature. The population of each state (in
Thousands) is given by:

Does the new-states paradox occur using Hamiltonʹs method of apportionment?
A) Yes
B) No

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the problem.
Which fairness criterion may be violated by any of the voting methods?
A) monotonicity criterion
B) head-to-head criterion
C) majority criterion
D) irrelevant alternatives criterion
Which fairness criterion may be violated by any of the voting methods?
A) monotonicity criterion
B) head-to-head criterion
C) majority criterion
D) irrelevant alternatives criterion

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
Which voting method may violate the monotonicity criterion?
A) plurality with elimination
B) Borda count
C) plurality
D) pairwise comparison
Which voting method may violate the monotonicity criterion?
A) plurality with elimination
B) Borda count
C) plurality
D) pairwise comparison

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
Which voting method always satisfies the head-to-head criterion?
A) plurality with elimination
B) Borda count
C) pairwise comparison
D) plurality
Which voting method always satisfies the head-to-head criterion?
A) plurality with elimination
B) Borda count
C) pairwise comparison
D) plurality

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck


