Deck 5: Exponents and Polynomials
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/122
Play
Full screen (f)
Deck 5: Exponents and Polynomials
1
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Trinomial, degree 6
B) Binomial, degree 7
C) Trinomial, degree 7
D) Trinomial, degree 8
A) Trinomial, degree 6
B) Binomial, degree 7
C) Trinomial, degree 7
D) Trinomial, degree 8
Trinomial, degree 6
2
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Binomial, degree 19
B) Binomial, degree 9
C) Monomial, degree 19
D) Monomial, degree 9
A) Binomial, degree 19
B) Binomial, degree 9
C) Monomial, degree 19
D) Monomial, degree 9
Monomial, degree 9
3
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
8
A) Monomial, degree 0
B) Monomial, degree 1
C) Monomial, degree 8
D) Binomial, degree 0
8
A) Monomial, degree 0
B) Monomial, degree 1
C) Monomial, degree 8
D) Binomial, degree 0
Monomial, degree 0
4
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Binomial, degree 0
B) Monomial, degree -16
C) Binomial, degree 2
D) Binomial, degree 1
A) Binomial, degree 0
B) Monomial, degree -16
C) Binomial, degree 2
D) Binomial, degree 1

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
5
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Binomial, degree -13
B) Binomial, degree 0
C) Monomial, degree 2
D) Monomial, degree -13
A) Binomial, degree -13
B) Binomial, degree 0
C) Monomial, degree 2
D) Monomial, degree -13

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
6
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Trinomial, degree 3
B) Trinomial, degree 5
C) Trinomial, degree 6
D) Binomial, degree 3
A) Trinomial, degree 3
B) Trinomial, degree 5
C) Trinomial, degree 6
D) Binomial, degree 3

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
7
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Binomial, degree 9
B) Trinomial, degree 9
C) Trinomial, degree 4
D) Binomial, degree 3
A) Binomial, degree 9
B) Trinomial, degree 9
C) Trinomial, degree 4
D) Binomial, degree 3

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
8
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
-14x
A) Monomial, degree 1
B) Monomial, degree 0
C) Monomial, degree -14
D) Binomial, degree 0
-14x
A) Monomial, degree 1
B) Monomial, degree 0
C) Monomial, degree -14
D) Binomial, degree 0

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
9
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
10
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
11
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
12
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
13
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
14
Identify the polynomial as a monomial, binomial, or trinomial. Give the degree of the polynomial.
A) Monomial, degree -8
B) Binomial, degree 0
C) Binomial, degree 7
D) Binomial, degree 6
A) Monomial, degree -8
B) Binomial, degree 0
C) Binomial, degree 7
D) Binomial, degree 6

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
15
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
16
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
17
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
18
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
19
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
20
Add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
21
Perform the indicated operations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
22
Use a vertical format to subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
23
Use a vertical format to subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
24
Subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
25
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
26
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
27
Subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
28
Use a vertical format to subtract the polynomials.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
29
Subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
30
Use a vertical format to add the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
31
Perform the indicated operations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
32
Use a vertical format to add the polynomials.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
33
Subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
34
Use a vertical format to subtract the polynomials.
-
A) \end{tabular}
B)
C)
D)
-
A) \end{tabular}
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
35
Use a vertical format to subtract the polynomials.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
36
Subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
37
Perform the indicated operations.
The bar graph shows the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and for women, W, who have
Completed x years of education. Find a mathematical model for M - W and use it to calculate the difference in the median annual income between
Men and women with 10 years of education. Does the model underestimate or overestimate the actual
Difference?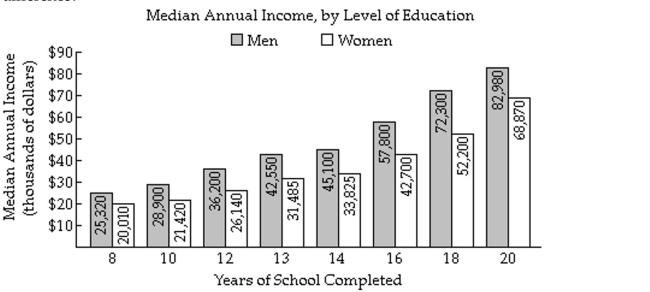
A) $16,433; overestimates
B) $4987; underestimates
C) $6213; underestimates
D) $9653; overestimates
The bar graph shows the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and for women, W, who have
Completed x years of education. Find a mathematical model for M - W and use it to calculate the difference in the median annual income between
Men and women with 10 years of education. Does the model underestimate or overestimate the actual
Difference?

A) $16,433; overestimates
B) $4987; underestimates
C) $6213; underestimates
D) $9653; overestimates

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
38
Subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
39
Perform the indicated operations.
Subtract -6 - 2x7 + 5x8 - 9x6 + 9x from the sum of -4x6 + 9x + 9 and 9x8 + 4x7.
A) 4x8 + 6x7 + 5x6 + 15
B) 14x8 + 2x7 - 13x6 + 15
C) 14x8 + 2x7 - 13x6 + 3
D) 4x8 + 2x7 - 13x6 + 3
Subtract -6 - 2x7 + 5x8 - 9x6 + 9x from the sum of -4x6 + 9x + 9 and 9x8 + 4x7.
A) 4x8 + 6x7 + 5x6 + 15
B) 14x8 + 2x7 - 13x6 + 15
C) 14x8 + 2x7 - 13x6 + 3
D) 4x8 + 2x7 - 13x6 + 3

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
40
Use a vertical format to subtract the polynomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
41
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
42
Graph the equation. Find seven solutions in your table of values for the equation by using integers for x, starting with -3
and ending with 3.
-
A)
B)
C)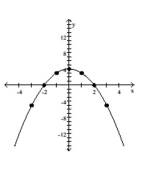
D)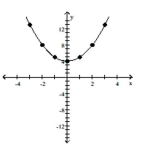
and ending with 3.
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
43
Simplify the expression using the products-to-powers rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
44
Multiply the expression using the product rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
45
Multiply the expression using the product rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
46
Graph the equation. Find seven solutions in your table of values for the equation by using integers for x, starting with -3
and ending with 3.
A census was taken to determine the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and
For women, W, who have completed x years of education. Shown in a rectangular coordinate system are the
Graphs of the polynomial models. Identify the median annual income for a man with 10 years of education as a
Point on the appropriate graph.
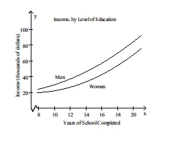
A) (10, 41,240)
B) (10, 58,431)
C) (10, 29,846)
D) (10, 22,161)
and ending with 3.
A census was taken to determine the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and
For women, W, who have completed x years of education. Shown in a rectangular coordinate system are the
Graphs of the polynomial models. Identify the median annual income for a man with 10 years of education as a
Point on the appropriate graph.

A) (10, 41,240)
B) (10, 58,431)
C) (10, 29,846)
D) (10, 22,161)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
47
Multiply the expression using the product rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
48
Simplify the expression using the products-to-powers rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
49
Simplify the expression using the power rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
50
Perform the indicated operations.
The bar graph shows the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and for women, W, who have
Completed x years of education. Find a mathematical model for M - W and use it to calculate the difference in the median annual income between
Men and women with 8 years of education. Does the model underestimate or overestimate the actual
Difference?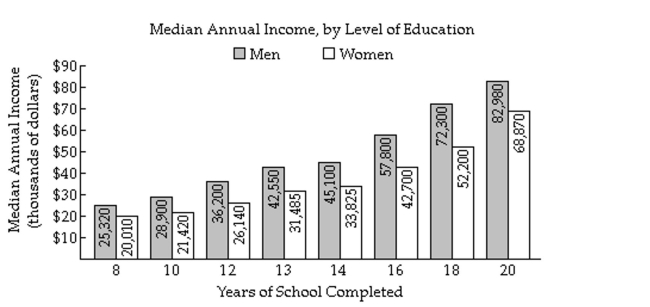
A) $4533; underestimates
B) $1325; underestimates
C) $14,019; overestimates
D) $5843; overestimates
The bar graph shows the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and for women, W, who have
Completed x years of education. Find a mathematical model for M - W and use it to calculate the difference in the median annual income between
Men and women with 8 years of education. Does the model underestimate or overestimate the actual
Difference?

A) $4533; underestimates
B) $1325; underestimates
C) $14,019; overestimates
D) $5843; overestimates

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
51
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
52
Multiply the expression using the product rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
53
Simplify the expression using the products-to-powers rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
54
Graph the equation. Find seven solutions in your table of values for the equation by using integers for x, starting with -3
and ending with 3.
-
A)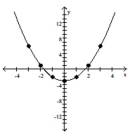
B)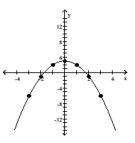
C)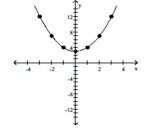
D)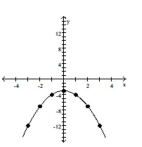
and ending with 3.
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
55
Graph the equation. Find seven solutions in your table of values for the equation by using integers for x, starting with -3
and ending with 3.
A census was taken to determine the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and
For women, W, who have completed x years of education. Shown in a rectangular coordinate system are the
Graphs of the polynomial models. Identify the median annual income for a woman with 13 years of education as
A point on the appropriate graph.
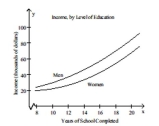
A) (13, 41,504)
B) (13, 56,696)
C) (13, 29,874)
D) (13, 78,234)
and ending with 3.
A census was taken to determine the median annual income for residents of a selected region of the United States, by level of education. The given polynomial models describe the median annual income for men, M, and
For women, W, who have completed x years of education. Shown in a rectangular coordinate system are the
Graphs of the polynomial models. Identify the median annual income for a woman with 13 years of education as
A point on the appropriate graph.

A) (13, 41,504)
B) (13, 56,696)
C) (13, 29,874)
D) (13, 78,234)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
56
Simplify the expression using the power rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
57
Graph the equation. Find seven solutions in your table of values for the equation by using integers for x, starting with -3
and ending with 3.
-
A)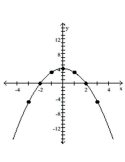
B)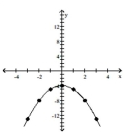
C)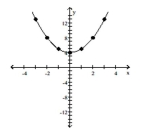
D)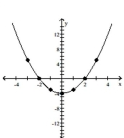
and ending with 3.
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
58
Simplify the expression using the products-to-powers rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
59
Simplify the expression using the products-to-powers rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
60
Simplify the expression using the power rule.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
61
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
62
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
63
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
Find the area of a triangle with a base of 7x inches and a height of (10x + 4) inches.
A) sq. in.
B) sq. in.
C) sq. in.
D) sq. in.
Find the area of a triangle with a base of 7x inches and a height of (10x + 4) inches.
A) sq. in.
B) sq. in.
C) sq. in.
D) sq. in.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
65
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
66
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
67
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
68
Multiply the monomials.
A)
B)
C) - \frac { 1 } { 20 } x ^ { 63 }\)
D)
A)
B)
C) - \frac { 1 } { 20 } x ^ { 63 }\)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
69
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
70
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
71
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
72
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
73
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
74
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
75
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
76
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
77
Multiply the monomials.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
78
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
79
Find the product.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the problem.
Write an expression for the area of the larger rectangle below in two different ways.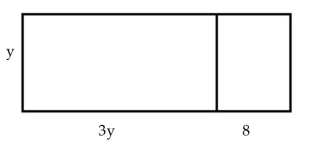
A)
B) ;
C) ;
D)
Write an expression for the area of the larger rectangle below in two different ways.

A)
B) ;
C) ;
D)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck


