Deck 5: Inverse, Exponential, and Logarithmic Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/472
Play
Full screen (f)
Deck 5: Inverse, Exponential, and Logarithmic Functions
1
Determine whether or not the function is one-to-one.
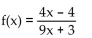
A) Yes
B) No
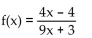
A) Yes
B) No
A
2
Determine whether or not the function is one-to-one.
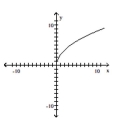
A) No
B) Yes

A) No
B) Yes
B
3
Determine whether or not the function is one-to-one.
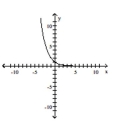
A) No
B) Yes

A) No
B) Yes
B
4
Decide whether the given functions are inverses.

A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether or not the function is one-to-one.
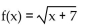
A) Yes
B) No
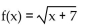
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether or not the function is one-to-one.
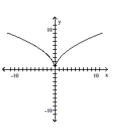
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether or not the function is one-to-one.
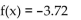
A) No
B) Yes
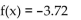
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
8
Determine whether or not the function is one-to-one.
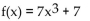
A) Yes
B) No
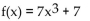
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
9
Determine whether or not the function is one-to-one.
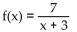
A) No
B) Yes
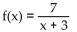
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether or not the function is one-to-one.
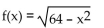
A)No
B) Yes
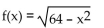
A)No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether or not the function is one-to-one.
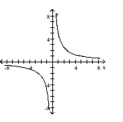
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether or not the function is one-to-one.
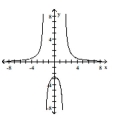
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
13
Decide whether the given functions are inverses.

A) Yes
B) No

A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether or not the function is one-to-one.
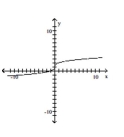
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
15
Determine whether or not the function is one-to-one.
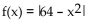
A) Yes
B) No
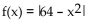
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
16
Determine whether or not the function is one-to-one.
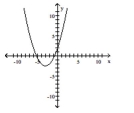
A) Yes
B) No

A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
17
Determine whether or not the function is one-to-one.
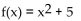
A) No
B) Yes
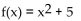
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether or not the function is one-to-one.
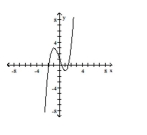
A) Yes
B) No

A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
19
Determine whether or not the function is one-to-one.
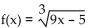
A) Yes
B) No
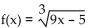
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
20
Determine whether or not the function is one-to-one.
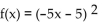
A) Yes
B) No
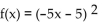
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
21
Decide whether the given functions are inverses.
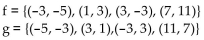
A) No
B) Yes
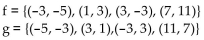
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
22
Decide whether the pair of functions graphed are inverses.
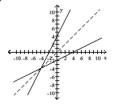
A) Yes
B) No

A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
23
Decide whether the given functions are inverses.
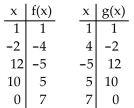
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
24
Use the definition of inverses to determine whether f and g are inverses.
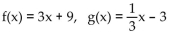
A) Yes
B) No
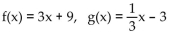
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
25
Use the definition of inverses to determine whether f and g are inverses.
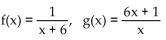
A) No
B) Yes
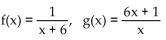
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
26
Use the definition of inverses to determine whether f and g are inverses.
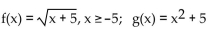
A) No
B) Yes
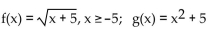
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
27
Decide whether the given functions are inverses.
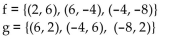
A) No
B) Yes
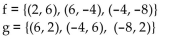
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
28
Use the definition of inverses to determine whether f and g are inverses.
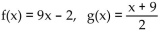
A) Yes
B) No
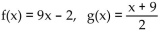
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
29
Decide whether the given functions are inverses.

A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
30
Decide whether the given functions are inverses.
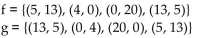
A) Yes
B) No
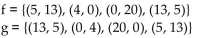
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
31
Decide whether the pair of functions graphed are inverses.
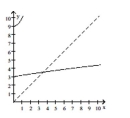
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
32
Use the definition of inverses to determine whether f and g are inverses.
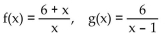
A) Yes
B) No
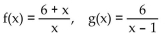
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
33
Decide whether the pair of functions graphed are inverses.
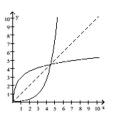
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
34
Use the definition of inverses to determine whether f and g are inverses.
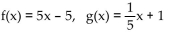
A) Yes
B) No
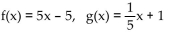
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
35
Decide whether the pair of functions graphed are inverses.
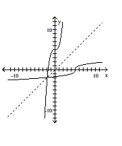
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
36
Decide whether the pair of functions graphed are inverses.
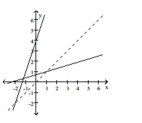
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
37
Use the definition of inverses to determine whether f and g are inverses.
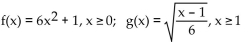
A) No
B) Yes
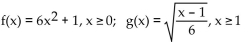
A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
38
Decide whether the given functions are inverses.

A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
39
Use the definition of inverses to determine whether f and g are inverses.
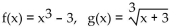
A) Yes
B) No
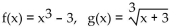
A) Yes
B) No

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
40
Decide whether the given functions are inverses.
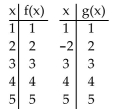
A) No
B) Yes

A) No
B) Yes

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
41
An everyday activity is described. Keeping in mind that an inverse operation "undoes" what an operation does, describe
each inverse activity.
waking up
A) closing the eyes
B) falling asleep
C) getting up
D) going to bed
each inverse activity.
waking up
A) closing the eyes
B) falling asleep
C) getting up
D) going to bed

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
42
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
43
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
44
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
45
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
46
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
47
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
48
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
49
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
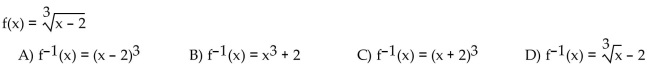
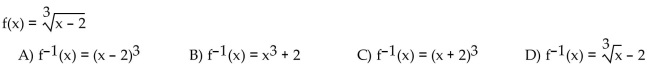

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
50
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
51
An everyday activity is described. Keeping in mind that an inverse operation "undoes" what an operation does, describe
each inverse activity.
opening a door
A) closing the door
B) locking the door
C) opening the window
D) going out of the door
each inverse activity.
opening a door
A) closing the door
B) locking the door
C) opening the window
D) going out of the door

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
52
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
{(-2, 4), (2, -4), (8, -2), (-8, 2)}
A) not one-to-one
B) {(4, -2), (-4, 2), (-2, -8), (2, 8)}
C) {(4, -2), (-4, 2), (8, -2), (2, -8)}
D) {(4, -2), (-4, 2), (-2, 8), (2, -8)}
{(-2, 4), (2, -4), (8, -2), (-8, 2)}
A) not one-to-one
B) {(4, -2), (-4, 2), (-2, -8), (2, 8)}
C) {(4, -2), (-4, 2), (8, -2), (2, -8)}
D) {(4, -2), (-4, 2), (-2, 8), (2, -8)}

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
53
An everyday activity is described. Keeping in mind that an inverse operation "undoes" what an operation does, describe
each inverse activity.
setting a clock forward by one hour
A) moving your schedule backward by one hour
B) leaving the clock as it is
C) setting the clock forward by two hours
D) setting the clock backward by one hour
each inverse activity.
setting a clock forward by one hour
A) moving your schedule backward by one hour
B) leaving the clock as it is
C) setting the clock forward by two hours
D) setting the clock backward by one hour

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
54
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
{(3, -5), (5, -3), (9, 2), (-9, -2)} 49)
A) {(-2, 9), (9, 5), (-5, 3), (2, -9)}
B) {(-5, 3), (-3, 5), (2, 9), (-2, -9)}
C) not one-to-one
D) {(-2, 9), (-3, 5), (-5, 5), (2, -9)}
{(3, -5), (5, -3), (9, 2), (-9, -2)} 49)
A) {(-2, 9), (9, 5), (-5, 3), (2, -9)}
B) {(-5, 3), (-3, 5), (2, 9), (-2, -9)}
C) not one-to-one
D) {(-2, 9), (-3, 5), (-5, 5), (2, -9)}

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
55
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
{(6, -7), (11, -6), (9, -5), (7, -4)}
A) {(7, 6), (6, 11), (-5, 9), (-4, 7)}
B) {(6, -7), (11, -6), (9, -5), (7, -4)}
C) {(-7, 6), (-6, 11), (-5, 9), (-4, 7)}
D) not one-to-one
{(6, -7), (11, -6), (9, -5), (7, -4)}
A) {(7, 6), (6, 11), (-5, 9), (-4, 7)}
B) {(6, -7), (11, -6), (9, -5), (7, -4)}
C) {(-7, 6), (-6, 11), (-5, 9), (-4, 7)}
D) not one-to-one

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
56
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
{(-3, -4), (-2, -4), (-1, 3), (0, 8)}
A) {(-4, -3), (8, 3), (-1, -2)}
B) {(-4, -3), (-2, 3), (-1, 8)}
C) {(-3, 8), (-3, 3), (-1, -2)}
D) not one-to-one
{(-3, -4), (-2, -4), (-1, 3), (0, 8)}
A) {(-4, -3), (8, 3), (-1, -2)}
B) {(-4, -3), (-2, 3), (-1, 8)}
C) {(-3, 8), (-3, 3), (-1, -2)}
D) not one-to-one

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
57
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
{(13, -6), (-5, 5), (6, -20)}
A) not one-to-one
B) {(13, 5), (13, -5), (-20, 6)}
C) {(-6, 13), (5, -5), (-20, 6)}
D) {(-6, 13), (6, -5), (-20, 5)}
{(13, -6), (-5, 5), (6, -20)}
A) not one-to-one
B) {(13, 5), (13, -5), (-20, 6)}
C) {(-6, 13), (5, -5), (-20, 6)}
D) {(-6, 13), (6, -5), (-20, 5)}

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
58
Use a graphing calculator to graph the function using the given viewing window. Use the graph to decide if the function
is one-to-one. If the function is one-to-one, give the equation of the inverse function.
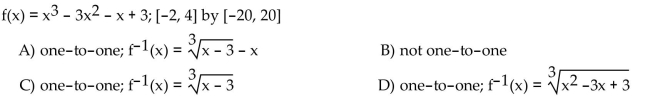
is one-to-one. If the function is one-to-one, give the equation of the inverse function.
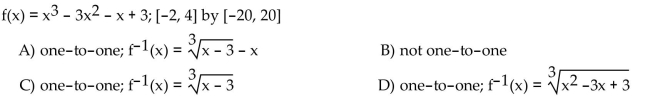

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
59
If the function is one-to-one, find its inverse. If not, write "not one-to-one."
{(4, 5), (7, 5), (1, 4)}
A) not one-to-one
B) {(4, 5), (5, 7), (4, 1)}
C) {(5, 4), (1, 7), (4, 5)}
D) {(5, 4), (5, 7), (4, 1)}
{(4, 5), (7, 5), (1, 4)}
A) not one-to-one
B) {(4, 5), (5, 7), (4, 1)}
C) {(5, 4), (1, 7), (4, 5)}
D) {(5, 4), (5, 7), (4, 1)}

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
60
If the function is one-to-one, find its inverse. If not, write "not one-to-one."



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
61
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
62
For the function as defined that is one-to-one, graph f and  on the same axes.
on the same axes.
 on the same axes.
on the same axes.

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
63
Use a graphing calculator to graph the function using the given viewing window. Use the graph to decide if the function
is one-to-one. If the function is one-to-one, give the equation of the inverse function.

is one-to-one. If the function is one-to-one, give the equation of the inverse function.


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
64
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
65
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
66
For the function as defined that is one-to-one, graph f and 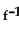 on the same axes.
on the same axes.
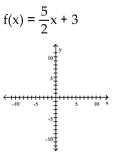
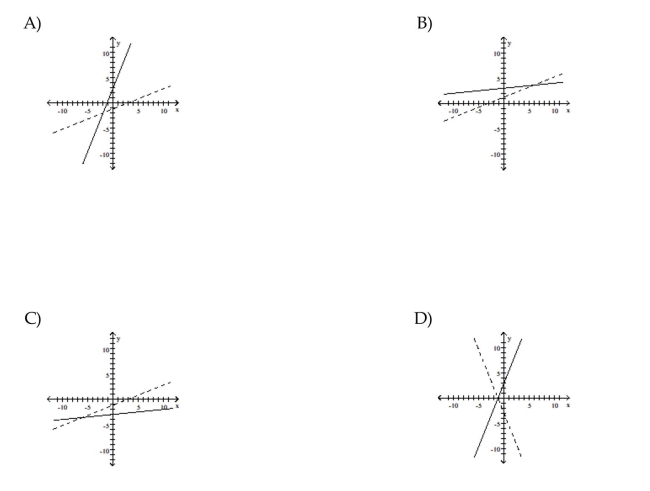
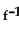 on the same axes.
on the same axes.


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
67
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
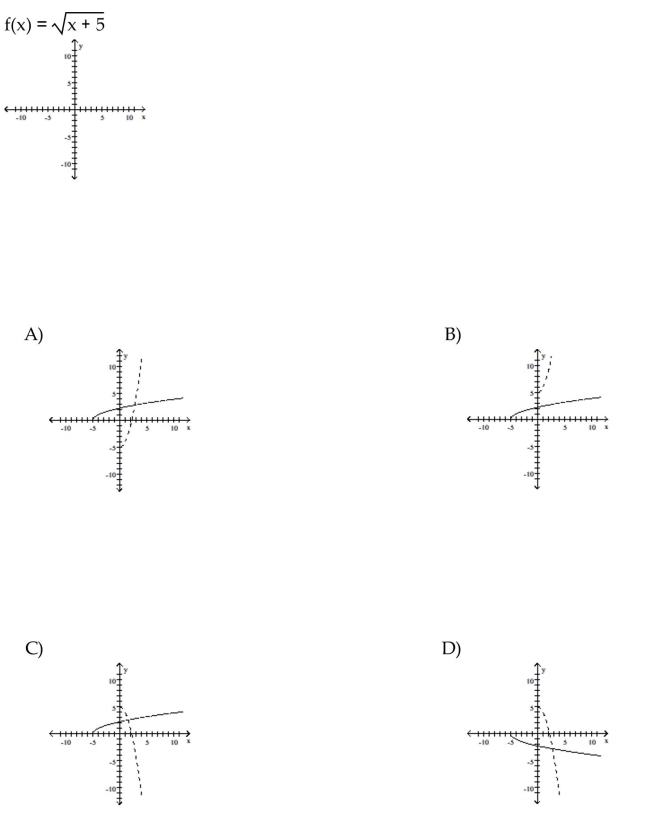
68
Use the graph of f to sketch a graph of the inverse of f using a dashed curve.
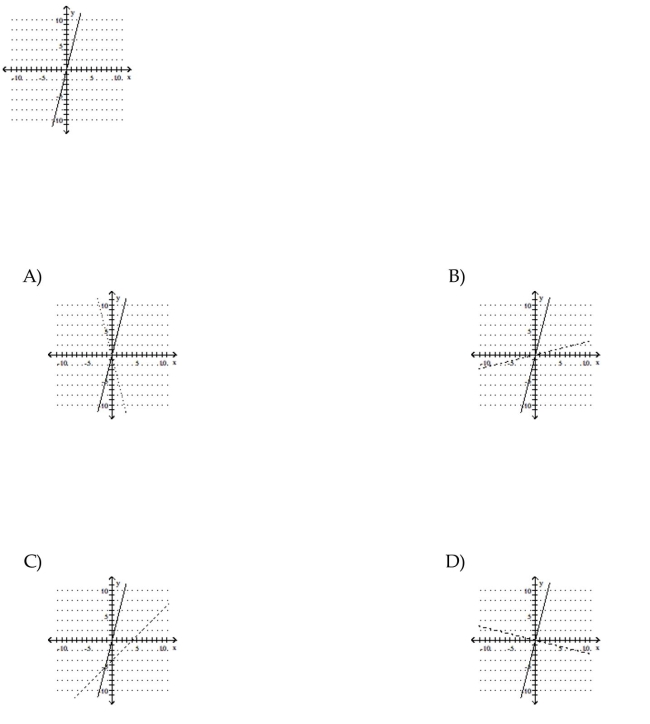


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
69
Use a graphing calculator to graph the function using the given viewing window. Use the graph to decide if the function
is one-to-one. If the function is one-to-one, give the equation of the inverse function.

is one-to-one. If the function is one-to-one, give the equation of the inverse function.


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
70
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
71
Find the domain and range of the inverse of the given function.
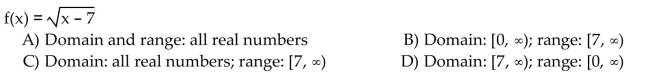
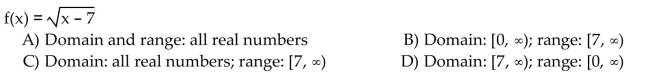

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
72
For the function as defined that is one-to-one, graph f and 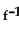 on the same axes.
on the same axes.
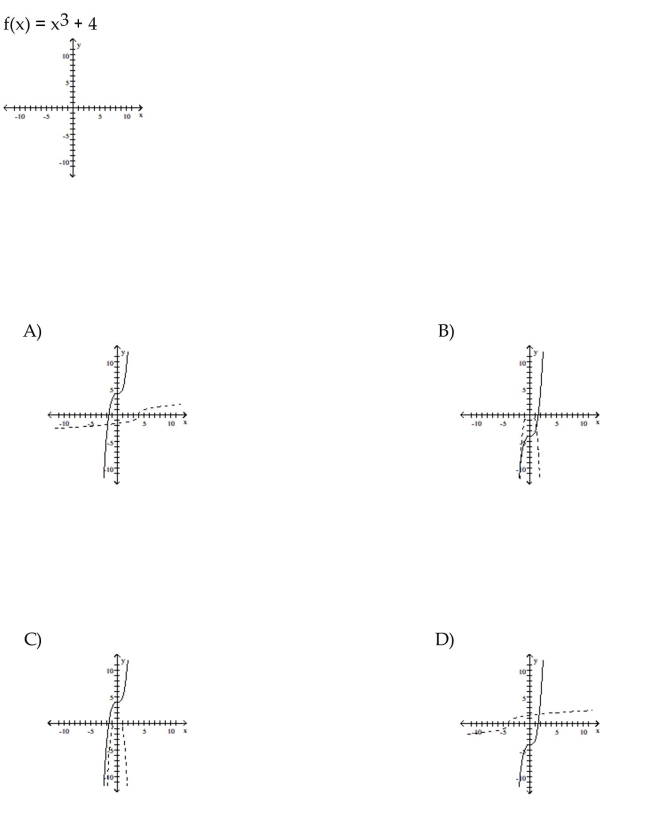
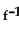 on the same axes.
on the same axes.

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
73
Use the graph of f to sketch a graph of the inverse of f using a dashed curve.
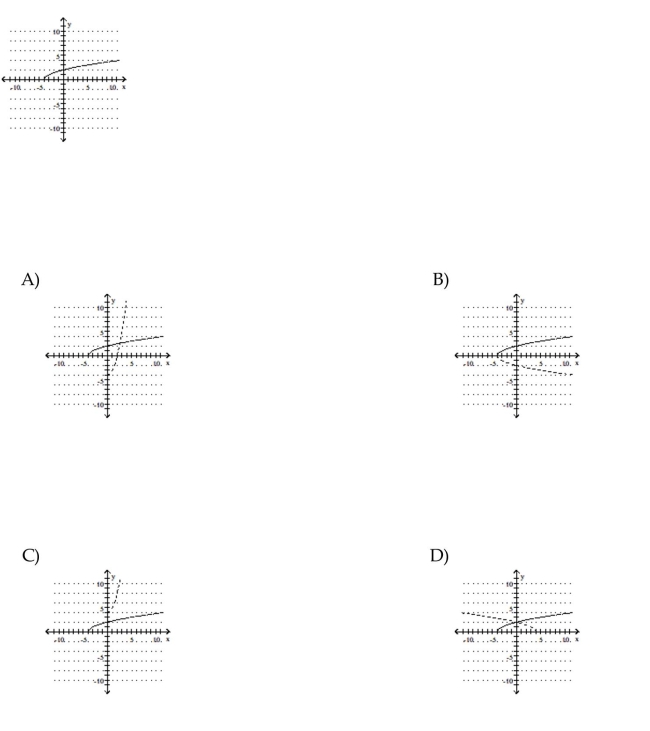


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
74
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
75
Use a graphing calculator to graph the function using the given viewing window. Use the graph to decide if the function
is one-to-one. If the function is one-to-one, give the equation of the inverse function.

is one-to-one. If the function is one-to-one, give the equation of the inverse function.


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
76
For the function as defined that is one-to-one, graph f and 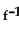 on the same axes.
on the same axes.
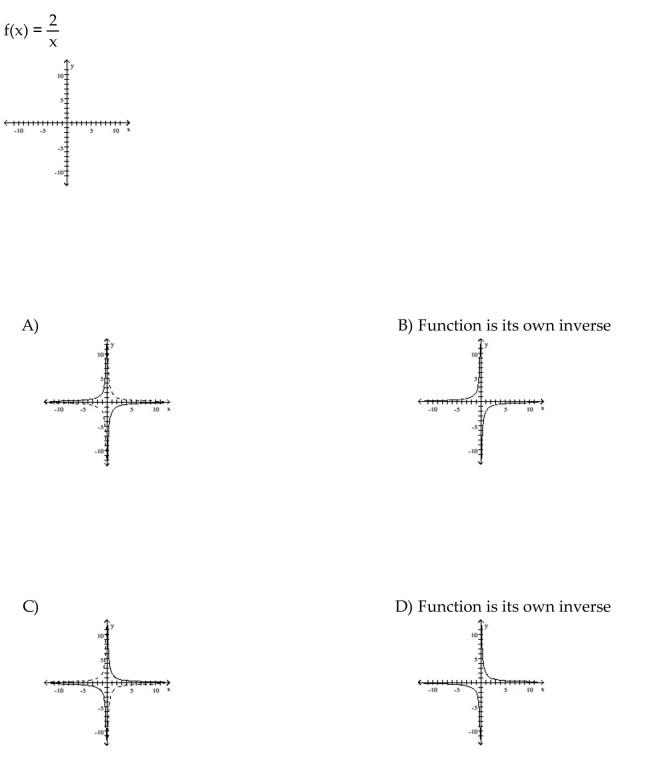
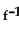 on the same axes.
on the same axes.

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
77
For the function as defined that is one-to-one, graph f and 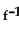 on the same axes.
on the same axes.
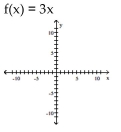
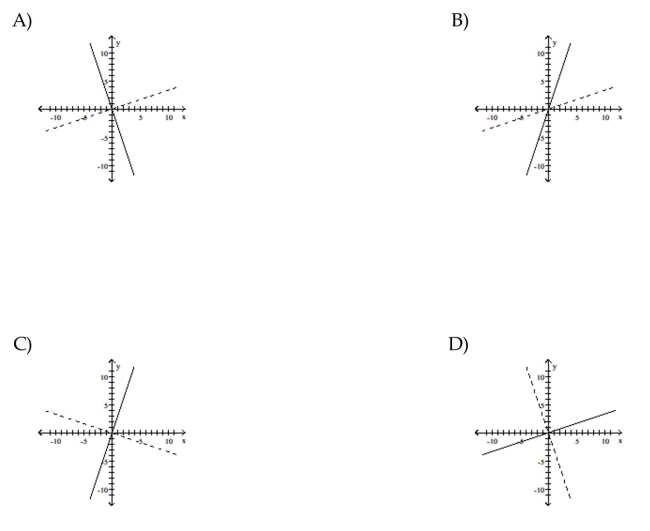
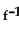 on the same axes.
on the same axes.


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
78
For the function as defined that is one-to-one, graph f and 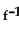 on the same axes.
on the same axes.
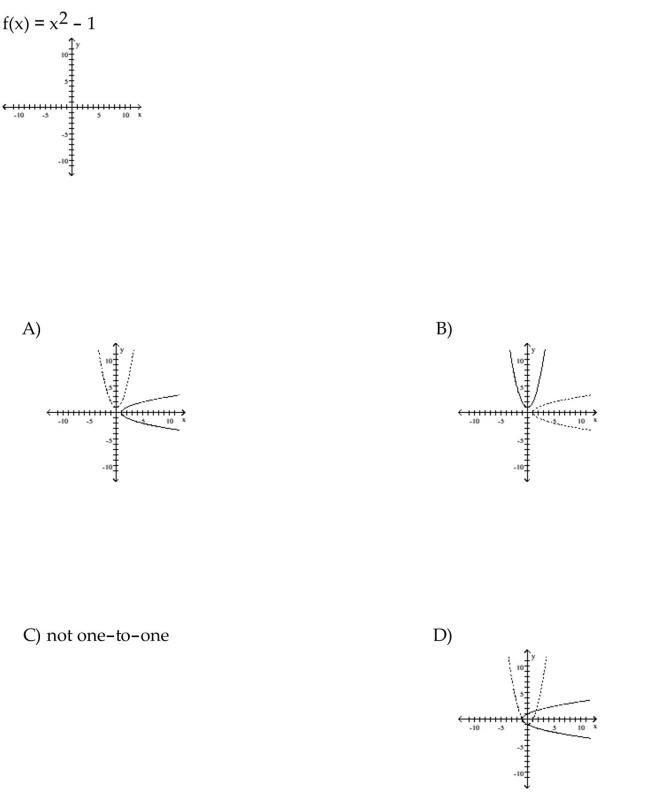
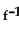 on the same axes.
on the same axes.

Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
79
Find the domain and range of the inverse of the given function.



Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck
80
Use the graph of f to sketch a graph of the inverse of f using a dashed curve.
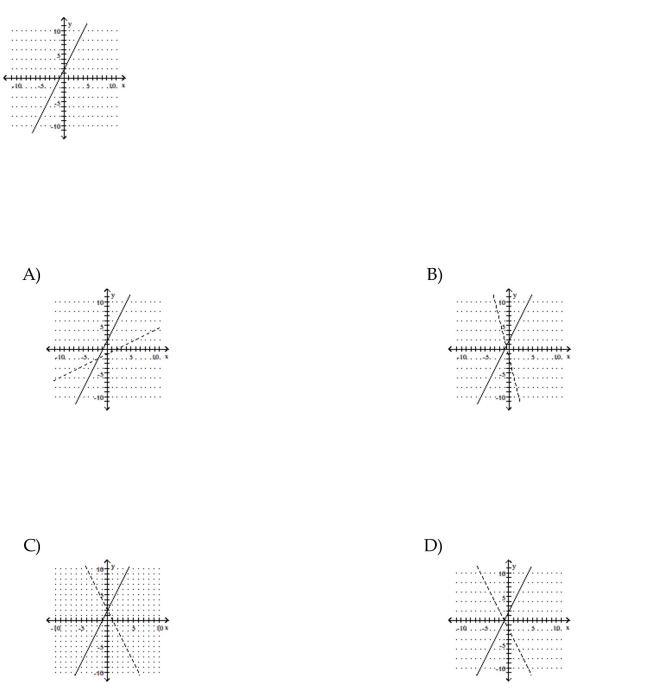


Unlock Deck
Unlock for access to all 472 flashcards in this deck.
Unlock Deck
k this deck


