Deck 8: Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/102
Play
Full screen (f)
Deck 8: Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses
1
University administrators are trying to decide where to build a new parking garage on campus. The state legislature has budgeted just enough money for one parking structure on campus. The administrators have determined that the parking garage will be built either by the college of engineering or by the college of business. To help make the final decision, the university has
Randomly and independently asked students from each of the two colleges to estimate how long they usually take to find a parking spot on campus (in minutes). Suppose that the sample sizes selected by the university for the two samples were both ne = nb= 15. What critical value should be used by the university in the calculations for the 95% confidence interval for µe - µb? Assume that the university used the pooled estimate of the population variances in the calculation of the
Confidence interval.
A)
B)
C)
D)
E)
Randomly and independently asked students from each of the two colleges to estimate how long they usually take to find a parking spot on campus (in minutes). Suppose that the sample sizes selected by the university for the two samples were both ne = nb= 15. What critical value should be used by the university in the calculations for the 95% confidence interval for µe - µb? Assume that the university used the pooled estimate of the population variances in the calculation of the
Confidence interval.
A)
B)
C)
D)
E)
2
A marketing study was conducted to compare the mean age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female purchasers of the product. It was desired to test to determine if the mean age of all female purchasers exceeds the mean age of all male purchasers. The sample data is shown here:
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Use the pooled estimate of the population standard deviation to calculate the value of the test statistic to use in this test of hypothesis.
A)
B)
C)
D)
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Use the pooled estimate of the population standard deviation to calculate the value of the test statistic to use in this test of hypothesis.
A)
B)
C)
D)
3
Consider the following set of salary data: 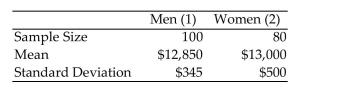 What assumptions are necessary to perform a test for the difference in population means?
What assumptions are necessary to perform a test for the difference in population means?
A) Both of the target populations have approximately normal distributions.
B) The population variances of salaries for men and women are equal.
C) The two samples were independently selected from the populations of men and women.
D) All of the above are necessary.
 What assumptions are necessary to perform a test for the difference in population means?
What assumptions are necessary to perform a test for the difference in population means?A) Both of the target populations have approximately normal distributions.
B) The population variances of salaries for men and women are equal.
C) The two samples were independently selected from the populations of men and women.
D) All of the above are necessary.
C
4
A marketing study was conducted to compare the mean age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female purchasers of the product. It was desired to test to determine if the mean age of all female purchasers exceeds the mean age of all male purchasers. The sample data is shown here:
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Find the rejection region to state the correct conclusion when testing at alpha .
A) Reject if
B) Reject if
C) Reject if
D) Reject if
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Find the rejection region to state the correct conclusion when testing at alpha .
A) Reject if
B) Reject if
C) Reject if
D) Reject if

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
5
An inventor has developed a new spray coating that is designed to improve the wear of bicycle tires. To test the new coating, the inventor randomly selects one of the two tires on each of 50 bicycles to be coated with the new spray. The bicycle is then driven for 100 miles and the amount of the depth of the tread left on the two bicycle tires is measured (in millimeters). It is desired to determine whether the new spray coating improves the wear of the bicycle tires. The data and summary information is shown below:
Use the summary data to construct a 90% confidence interval for the difference between the means.
A)
B)
C)
D)
Use the summary data to construct a 90% confidence interval for the difference between the means.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
6
In a controlled laboratory environment, a random sample of 10 adults and a random sample of 10 children were tested by a psychologist to determine the room temperature that each person finds most comfortable. The data are summarized below:
If the psychologist wished to test the hypothesis that children prefer warmer room temperatures than adults, which set of hypotheses would he use?
A) vs.
B) vs.
C) vs.
D) vs.
If the psychologist wished to test the hypothesis that children prefer warmer room temperatures than adults, which set of hypotheses would he use?
A) vs.
B) vs.
C) vs.
D) vs.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
7
A marketing study was conducted to compare the mean age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female purchasers of the product. What type of analysis should be used to compare the mean age of male and female purchasers?
A) An independent samples comparison of population proportions.
B) A paired difference comparison of population means.
C) An independent samples comparison of population means.
D) A test of a single population mean.
A) An independent samples comparison of population proportions.
B) A paired difference comparison of population means.
C) An independent samples comparison of population means.
D) A test of a single population mean.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
8
Data was collected from CEOs of companies within both the low-tech industry and the consumer products industry. The following printout compares the mean return-to-pay ratios between CEOs in the low-tech industry with CEOs in the consumer products industry.
Using the printout, which of the following assumptions is not necessary for the test to be valid?
A) The population variances are equal.
B) The samples were randomly and independently selected.
C) The population means are equal.
D) Both populations have approximately normal distributions.
Using the printout, which of the following assumptions is not necessary for the test to be valid?
A) The population variances are equal.
B) The samples were randomly and independently selected.
C) The population means are equal.
D) Both populations have approximately normal distributions.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
9
Salary data were collected from CEOs in the consumer products industry and CEOs in the telecommunication industry. The data were analyzed using a software package in order to compare mean salaries of CEOs in the two industries.
What of the following assumptions is necessary to perform the test described above?
A) The means of the two populations of salaries are equal.
B) The population of salaries for each of the two industries has an approximately normal distribution.
C) The standard deviations of the two populations of salaries are both large.
D) None. The Central Limit Theorem takes care of all assumptions
What of the following assumptions is necessary to perform the test described above?
A) The means of the two populations of salaries are equal.
B) The population of salaries for each of the two industries has an approximately normal distribution.
C) The standard deviations of the two populations of salaries are both large.
D) None. The Central Limit Theorem takes care of all assumptions

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
10
We are interested in comparing the average supermarket prices of two leading colas. Our sample was taken by randomly selecting eight supermarkets and recording the price of a six-pack of each brand of cola at each supermarket. The data are shown in the following table:
If the problem above represented a paired difference, what assumptions are needed for a confidence interval for the mean difference to be valid?
A) The population variances are equal.
B) The population of paired differences has an approximately normal distribution.
C) The samples were independently selected from each population.
D) All of the above are needed.
If the problem above represented a paired difference, what assumptions are needed for a confidence interval for the mean difference to be valid?
A) The population variances are equal.
B) The population of paired differences has an approximately normal distribution.
C) The samples were independently selected from each population.
D) All of the above are needed.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
11
When blood levels are low at an area hospital, a call goes out to local residents to give blood. The blood center is interested in determining which sex - males or females - is more likely to respond.
Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes of the male and female responses. Find the rejection region that would be used if it is desired to test to
Determine if a difference exists between the proportion of the females and males who responds to the call to donate blood.
A) Reject if or .
B) Reject if .
C) Reject if .
D) Reject if or .
Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes of the male and female responses. Find the rejection region that would be used if it is desired to test to
Determine if a difference exists between the proportion of the females and males who responds to the call to donate blood.
A) Reject if or .
B) Reject if .
C) Reject if .
D) Reject if or .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
12
We sampled 100 men and 100 women and asked: "Do you think the environment is a major concern?" Of those sampled, 67 women and 53 men responded that they believed it is. For the confidence interval procedure to work properly, what additional assumptions must be satisfied?
A) Both populations have approximate normal distributions.
B) Both samples were randomly and independently selected from their respective populations.
C) The population variances are equal.
D) All of the above are necessary.
A) Both populations have approximate normal distributions.
B) Both samples were randomly and independently selected from their respective populations.
C) The population variances are equal.
D) All of the above are necessary.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
13
A researcher is investigating which of two newly developed automobile engine oils is better at prolonging the life of an engine. Since there are a variety of automobile engines, 20 different engine types were randomly selected and were tested using each of the two engine oils. The number of
Hours of continuous use before engine breakdown was recorded for each engine oil. Based on the information provided, what type of analysis will yield the most useful information?
A) Matched pairs comparison of population proportions.
B) Independent samples comparison of population proportions.
C) Independent samples comparison of population means.
D) Matched pairs comparison of population means.
Hours of continuous use before engine breakdown was recorded for each engine oil. Based on the information provided, what type of analysis will yield the most useful information?
A) Matched pairs comparison of population proportions.
B) Independent samples comparison of population proportions.
C) Independent samples comparison of population means.
D) Matched pairs comparison of population means.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
14
When blood levels are low at an area hospital, a call goes out to local residents to give blood. The blood center is interested in determining which sex - males or females - is more likely to respond.
Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes between the male and female responses. What type of analysis should be used?
A) An independent samples comparison of population means.
B) A paired difference comparison of population means.
C) An independent samples comparison of population proportions.
D) A test of a single population proportion.
Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes between the male and female responses. What type of analysis should be used?
A) An independent samples comparison of population means.
B) A paired difference comparison of population means.
C) An independent samples comparison of population proportions.
D) A test of a single population proportion.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
15
Given 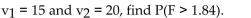
A) 0.05
B) 0.025
C) 0.10
D) 0.01
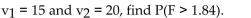
A) 0.05
B) 0.025
C) 0.10
D) 0.01

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
16
A marketing study was conducted to compare the mean age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female purchasers of the product. It was desired to test to determine if the mean age of all female purchasers exceeds the mean age of all male purchasers. The sample data is shown here:
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Which of the following assumptions must be true in order for the pooled test of hypothesis to be valid?
I. Both the male and female populations of ages must possess approximately normal probability distributions.
II. Both the male and female populations of ages must possess population variances that are equal.
III. Both samples of ages must have been randomly and independently selected from their respective populations.
A) I only
B) III only
C) II only
D) I, II, and III
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Which of the following assumptions must be true in order for the pooled test of hypothesis to be valid?
I. Both the male and female populations of ages must possess approximately normal probability distributions.
II. Both the male and female populations of ages must possess population variances that are equal.
III. Both samples of ages must have been randomly and independently selected from their respective populations.
A) I only
B) III only
C) II only
D) I, II, and III

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
17
A marketing study was conducted to compare the variation in the age of male and female purchasers of a certain product. Random and independent samples were selected for both male andfemale purchasers of the product. The sample data is shown here:
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Calculate the test statistics that should be used to determine if the variation in the female ages exceeds the variation in the male ages.
A)
B)
C)
D)
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Calculate the test statistics that should be used to determine if the variation in the female ages exceeds the variation in the male ages.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
18
A certain manufacturer is interested in evaluating two alternative manufacturing plans consisting of different machine layouts. Because of union rules, hours of operation vary greatly for this particular manufacturer from one day to the next. Twenty-eight random working days were selected and each plan was monitored and the number of items produced each day was recorded.
Some of the collected data is shown below: What assumptions are necessary for the above test to be valid?
A) None of these listed, since the Central Limit Theorem can be applied.
B) Both populations must be approximately normally distributed.
C) The population variances must be approximately equal.
D) The population of paired differences must be approximately normally distributed.
Some of the collected data is shown below: What assumptions are necessary for the above test to be valid?
A) None of these listed, since the Central Limit Theorem can be applied.
B) Both populations must be approximately normally distributed.
C) The population variances must be approximately equal.
D) The population of paired differences must be approximately normally distributed.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
19
The owners of an industrial plant want to determine which of two types of fuel (gas or electricity) will produce more useful energy at a lower cost. The cost is measured by plant investment per delivered quad ($ invested /quadrillion BTUs). The smaller this number, the less the industrial plant pays for delivered energy. Suppose we wish to determine if there is a difference in the average investment/quad between using electricity and using gas. Our null and alternative hypotheses would be:
A) vs.
B) vs.
C) vs.
D) vs.
A) vs.
B) vs.
C) vs.
D) vs.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
20
An inventor has developed a new spray coating that is designed to improve the wear of bicycle tires. To test the new coating, the inventor randomly selects one of the two tires on each of 50 bicycles to be coated with the new spray. The bicycle is then driven for 100 miles and the amount of the depth of the tread left on the two bicycle tires is measured (in millimeters). It is desired to determine whether the new spray coating improves the wear of the bicycle tires. The data and summary information is shown below:
Use the summary data to calculate the test statistic to determine if the new spray coating improves the mean wear of the bicycle tires.
A)
B)
C)
D)
Use the summary data to calculate the test statistic to determine if the new spray coating improves the mean wear of the bicycle tires.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
21
A marketing study was conducted to compare the variation in the age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female purchasers of the product. The sample data is shown here:
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Identify the rejection region to that should be used to determine if the variation in the female ages exceeds the variation in the male ages when testing at .
A)
B)
C) F >
D)
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Identify the rejection region to that should be used to determine if the variation in the female ages exceeds the variation in the male ages when testing at .
A)
B)
C) F >
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
22
An inventor has developed a new spray coating that is designed to improve the wear of bicycle tires. To test the new coating, the inventor randomly selects one of the two tires on each of 50 bicycles to be coated with the new spray. The bicycle is then driven for 100 miles and the amount of the depth of the tread left on the two bicycle tires is measured (in millimeters). It is desired to determine whether the new spray coating improves the wear of the bicycle tires. The data and summary information is shown below:
Identify the correct null and alternative hypothesis for testing whether the new spray coating improves the mean wear of the bicycle tires (which would result in a larger amount of tread left on the tire).
A) vs.
B) vs.
C) vs.
Identify the correct null and alternative hypothesis for testing whether the new spray coating improves the mean wear of the bicycle tires (which would result in a larger amount of tread left on the tire).
A) vs.
B) vs.
C) vs.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
23
A new type of band has been developed for children who have to wear braces. The new bands are designed to be more comfortable, look better, and provide more rapid progress in realigning teeth. An experiment was conducted to compare the mean wearing time necessary to correct a specific type of misalignment between the old braces and the new bands. One hundred children were randomly assigned, 50 to each group. A summary of the data is shown in the table.
How many patients would need to be sampled to estimate the difference in means to within 26 days with probability 99%?
How many patients would need to be sampled to estimate the difference in means to within 26 days with probability 99%?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
24
Which supermarket has the lowest prices in town? All claim to be cheaper, but an independent agency recently was asked to investigate this question. The agency randomly selected 100 items common to each of two supermarkets (labeled A and B) and recorded the prices charged by each supermarket. The summary results are provided below:
Assuming a matched pairs design, which of the following assumptions is necessary for a confidence interval for the mean difference to be valid?
A) None of these assumptions are necessary.
B) The samples are randomly and independently selected.
C) The population variances must be equal.
D) The population of paired differences has an approximate normal distribution.
Assuming a matched pairs design, which of the following assumptions is necessary for a confidence interval for the mean difference to be valid?
A) None of these assumptions are necessary.
B) The samples are randomly and independently selected.
C) The population variances must be equal.
D) The population of paired differences has an approximate normal distribution.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
25
A researcher is investigating which of two newly developed automobile engine oils is better at prolonging the life of an engine. Since there are a variety of automobile engines, 20 different engine types were randomly selected and were tested using each of the two engine oils. The number of
Hours of continuous use before engine breakdown was recorded for each engine oil. Suppose the following 95% confidence interval for was calculated: (100, 2500). Which of the following inferences is correct?
A) We are 95% confident that no significant differences exists in the mean number of hours of continuous use before breakdown of engines using oils A and B.
B) We are 95% confident that the mean number of hours of continuous use of an engine using oil A is between 100 and 2500 hours.
C) We are 95% confident that an engine using oil A has a higher mean number of hours of continuous use before breakdown than does an engine using oil B.
D) We are 95% confident that an engine using oil B has a higher mean number of hours of continuous use before breakdown than does an engine using oil A.
Hours of continuous use before engine breakdown was recorded for each engine oil. Suppose the following 95% confidence interval for was calculated: (100, 2500). Which of the following inferences is correct?
A) We are 95% confident that no significant differences exists in the mean number of hours of continuous use before breakdown of engines using oils A and B.
B) We are 95% confident that the mean number of hours of continuous use of an engine using oil A is between 100 and 2500 hours.
C) We are 95% confident that an engine using oil A has a higher mean number of hours of continuous use before breakdown than does an engine using oil B.
D) We are 95% confident that an engine using oil B has a higher mean number of hours of continuous use before breakdown than does an engine using oil A.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
26


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
27
Independent random samples from normal populations produced the results shown below.
Sample 1: 5.8, 5.1, 3.9, 4.5, 5.4
Sample 2: 4.4, 6.1, 5.2, 5.7
a. Calculate the pooled estimator of .
b. Test using .
c. Find a confidence interval for .
Sample 1: 5.8, 5.1, 3.9, 4.5, 5.4
Sample 2: 4.4, 6.1, 5.2, 5.7
a. Calculate the pooled estimator of .
b. Test using .
c. Find a confidence interval for .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
28
A certain manufacturer is interested in evaluating two alternative manufacturing plans consisting of different machine layouts. Because of union rules, hours of operation vary greatly for this particular manufacturer from one day to the next. Twenty-eight random working days were selected and each plan was monitored and the number of items produced each day was recorded. some of the collected data is shown below:
What type of analysis will best allow the manufacturer to determine which plan is more effective?
A) An independent samples comparison of population means.
B) An independent samples comparison of population proportions.
C) A paired difference comparison of population means.
D) A test of a single population proportion.
What type of analysis will best allow the manufacturer to determine which plan is more effective?
A) An independent samples comparison of population means.
B) An independent samples comparison of population proportions.
C) A paired difference comparison of population means.
D) A test of a single population proportion.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
29
Independent random samples selected from two normal populations produced the following sample means and standard deviations.
Find and interpret the confidence interval for .
Find and interpret the confidence interval for .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
30
A marketing study was conducted to compare the mean age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female purchasers of the product. It was desired to test to determine if the mean age of all female purchasers exceeds the mean age of all male purchasers. The sample data is shown here:
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Suppose the test statistic was calculated to be the value, . Use the rejection region to state the correct conclusion when testing at alpha .
A) We accept .
B) We fail to reject .
C) We reject .
Female: sample mean sample standard deviation
Male: sample mean sample standard deviation
Suppose the test statistic was calculated to be the value, . Use the rejection region to state the correct conclusion when testing at alpha .
A) We accept .
B) We fail to reject .
C) We reject .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
31
Suppose it desired to compare two physical education training programs for preadolescent girls. A total of 122 girls are randomly selected, with 61 assigned to each program. After three 6-week periods on the program, each girl is given a fitness test that yields a score between 0 and 100. The means and variances of the scores for the two groups are shown in the table.
Test to determine if the variances of the two programs differ. Use
Test to determine if the variances of the two programs differ. Use

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
32
Independent random samples, each containing 500 observations were selected from two binomial populations. The samples from populations 1 and 2 produced 210 and 320 successes, respectively

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose you want to estimate the difference between two population means correct to within 2.5 with probability 0.95. If prior information suggests that the population variances are both equal to the value 20, and you want to select independent random samples of equal size from the populations, how large should the sample sizes be?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
34
When blood levels are low at an area hospital, a call goes out to local residents to give blood. The blood center is interested in determining which sex - males or females - is more likely to respond.
Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes of the male and female responses. Suppose 45 of the females and 60 of the males responded that they were able to give blood. Find the test statistic that would be used if it is desired to test to determine if a difference exists between the proportion of the females and males who responds to the call to donate blood.
A)
B)
C)
D)
Random, independent samples of 60 females and 100 males were each asked if they would be willing to give blood when called by a local hospital. A success is defined as a person who responds to the call and donates blood. The goal is to compare the percentage of the successes of the male and female responses. Suppose 45 of the females and 60 of the males responded that they were able to give blood. Find the test statistic that would be used if it is desired to test to determine if a difference exists between the proportion of the females and males who responds to the call to donate blood.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
35
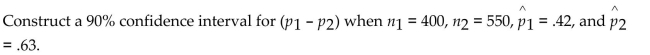

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
36
A new weight-reducing technique, consisting of a liquid protein diet, is currently undergoing tests by the Food and Drug Administration (FDA) before its introduction into the market. The weights of a random sample of five people are recorded before they are introduced to the liquid protein diet. The five individuals are then instructed to follow the liquid protein diet for 3 weeks. At the end of this period, their weights (in pounds) are again recorded. The results are listed in the table. Let be the true mean weight of individuals before starting the diet and let be the true mean weight of individuals after 3 weeks on the diet.
Summary information is as follows: .
Test to determine if the diet is effective at reducing weight. Use .
Summary information is as follows: .
Test to determine if the diet is effective at reducing weight. Use .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
37
In a controlled laboratory environment, a random sample of 10 adults and a random sample of 10 children were tested by a psychologist to determine the room temperature that each person finds most comfortable. The data are summarized below:
Suppose that the psychologist decides to construct a 99% confidence interval for the difference in mean comfortable room temperatures instead of proceeding with a test of hypothesis. The 99% confidence interval turns out to be (-2.9, 3.1). Select the correct statement.
A) It can be concluded at the 99% confidence level that the true mean comfortable room temperature for children exceeds that for adults.
B) It can be concluded at the 99% confidence level that the true mean room temperature for adults exceeds that for children.
C) It can be concluded at the 99% confidence level that the true mean comfortable room temperature is between -2.9 and 3.1.
D) It cannot be concluded at the 99% confidence level that there is actually a difference between the true mean comfortable room temperatures for the two groups.
Suppose that the psychologist decides to construct a 99% confidence interval for the difference in mean comfortable room temperatures instead of proceeding with a test of hypothesis. The 99% confidence interval turns out to be (-2.9, 3.1). Select the correct statement.
A) It can be concluded at the 99% confidence level that the true mean comfortable room temperature for children exceeds that for adults.
B) It can be concluded at the 99% confidence level that the true mean room temperature for adults exceeds that for children.
C) It can be concluded at the 99% confidence level that the true mean comfortable room temperature is between -2.9 and 3.1.
D) It cannot be concluded at the 99% confidence level that there is actually a difference between the true mean comfortable room temperatures for the two groups.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
38
In order to compare the means of two populations, independent random samples of 225 observations are selected from each population with the following results.
Test the null hypothesis against the alternative hypothesis using . Give the significance level, and interpret the result.
Test the null hypothesis against the alternative hypothesis using . Give the significance level, and interpret the result.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
39
University administrators are trying to decide where to build a new parking garage on campus. The state legislature has budgeted just enough money for one parking structure on campus. The administrators have determined that the parking garage will be built either by the college of engineering or by the college of business. To help make the final decision, the university has
Randomly and independently asked students from each of the two colleges to estimate how long they usually take to find a parking spot on campus (in minutes). Based on their sample, the following 95% confidence interval (for µe - µb) was created - (4.20, 10.20). What conclusion can the university make about the population mean parking times based on this confidence interval?
A) They are 95% confident that the mean parking time of all business students is less than the mean parking time of all engineering students.
B) They are 95% confident that the mean parking time of all business students exceeds the mean parking time of all engineering students.
C) They are 95% confident that the mean parking time of all business students equals the mean parking time of all engineering students.
Randomly and independently asked students from each of the two colleges to estimate how long they usually take to find a parking spot on campus (in minutes). Based on their sample, the following 95% confidence interval (for µe - µb) was created - (4.20, 10.20). What conclusion can the university make about the population mean parking times based on this confidence interval?
A) They are 95% confident that the mean parking time of all business students is less than the mean parking time of all engineering students.
B) They are 95% confident that the mean parking time of all business students exceeds the mean parking time of all engineering students.
C) They are 95% confident that the mean parking time of all business students equals the mean parking time of all engineering students.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
40


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
41
A paired difference experiment has 15 pairs of observations. What is the rejection region for testing .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether the sample sizes are large enough to conclude that the sampling distributions are approximately normal.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
43
Independent random samples selected from two normal populations produced the following sample means and standard deviations.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
44
A government housing agency is comparing home ownership rates among several immigrant groups. In a sample of 235 families who emigrated to the U.S. from Eastern europe five years ago, 165 now own homes. In a sample of 195 families who emigrated to the U.S. from Pacific islands five years ago, 125 now own homes. Write a 95% confidence interval for the difference in home ownership rates between the two groups. Based on the confidence interval, can you conclude that there is a significant difference in home
ownership rates in the two groups of immigrants?
ownership rates in the two groups of immigrants?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
45


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
46
Two surgical procedures are widely used to treat a certain type of cancer. To compare the success rates of the two procedures, random samples of surgical patients were obtained and the numbers of patients who showed no recurrence of the disease after a 1-year period were recorded. The data are shown in the table.
How large a sample would be necessary in order to estimate the difference in the true success rates to within .10 with 95% reliability?
How large a sample would be necessary in order to estimate the difference in the true success rates to within .10 with 95% reliability?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
47
In order to compare the means of two populations, independent random samples of 144 observations are selected from each population with the following results.
Use a 95\% confidence interval to estimate the difference between the population means . Interpret the confidence interval.
Use a 95\% confidence interval to estimate the difference between the population means . Interpret the confidence interval.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
48
A paired difference experiment yielded the following results.
Test against , where , using .
Test against , where , using .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
49
In an exit poll, 42 of 75 men sampled supported a ballot initiative to raise the local sales tax to build a new football stadium. In the same poll, 41 of 85 women sampled supported the initiative. Find and interpret the p-value for the test of hypothesis that the proportions of men and women who support the initiative are different.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
50
One indication of how strong the real estate market is performing is the proportion of properties that sell in less than 30 days after being listed. Of the condominiums in a Florida beach community that sold in the first six months of 2006, 75 of the 115 sampled had been on the market less than 30 days. For the first six months of 2007, 25 of the 85 sampled had been on the market less than 30 days. Test the hypothesis that the proportion of condominiums that sold within 30 days decreased from 2006 to 2007. Use

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
51
The data for a random sample of five paired observations are shown below. 


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
52
A new weight-reducing technique, consisting of a liquid protein diet, is currently undergoing tests by the Food and Drug Administration (FDA) before its introduction into the market. The weights of a random sample of five people are recorded before they are introduced to the liquid protein diet. The five individuals are then instructed to follow the liquid protein diet for 3 weeks. At the end of this period, their weights (in pounds) are again recorded. The results are listed in the table. Let µ1 be the true mean weight of
individuals before starting the diet and let µ2 be the true mean weight of individuals after 3 weeks on the diet.
Calculate a 90% confidence interval for the difference between the mean weights before and after the diet is used.
individuals before starting the diet and let µ2 be the true mean weight of individuals after 3 weeks on the diet.
Calculate a 90% confidence interval for the difference between the mean weights before and after the diet is used.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
53
A paired difference experiment has 75 pairs of observations. What is the rejection region for testing

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
54
A paired difference experiment produced the following results.
Perform the appropriate test to determine whether there is sufficient evidence to conclude that using .
Perform the appropriate test to determine whether there is sufficient evidence to conclude that using .

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
55
Determine whether the sample sizes are large enough to conclude that the sampling distributions are approximately normal.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
56
 Comment on the validity of the results.
Comment on the validity of the results.
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
57
The data for a random sample of six paired observations are shown below. 


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
58


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
59
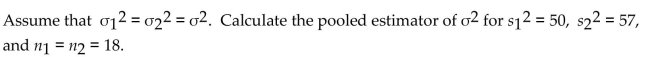

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
60
Independent random samples of 100 observations each are chosen from two normal populations with the following means and standard deviations.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
61
The FDA is comparing the mean caffeine contents of two brands of cola. Independent random samples of 6-oz. cans of each brand were selected and the caffeine content of each can determined. the study provided the following summary information.
How many cans of each soda would need to be sampled in order to estimate the difference in the mean caffeine content to within . 5 with reliability?
A)
B)
C)
D)
How many cans of each soda would need to be sampled in order to estimate the difference in the mean caffeine content to within . 5 with reliability?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
62
Which of the following represents the difference in two population proportions?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
63
Which supermarket has the lowest prices in town? All claim to be cheaper, but an independent agency recently was asked to investigate this question. The agency randomly selected 100 items common to each of two supermarkets (labeled A and B) and recorded the prices charged by each supermarket. The summary results are provided below:
Assuming the data represent a matched pairs design, calculate the confidence interval for comparing mean prices using a 95% confidence level.
A).
B).
C).10
D) .10
Assuming the data represent a matched pairs design, calculate the confidence interval for comparing mean prices using a 95% confidence level.
A).
B).
C).10
D) .10

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
64
The FDA is comparing the mean caffeine contents of two brands of cola. Independent random samples of 6-oz. cans of each brand were selected and the caffeine content of each can determined.
The study provided the following summary information.
The study provided the following summary information.


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
65
The sample standard deviation of differences sd is equal to the difference of the sample standard deviations s1 - s2

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
66
Specify the appropriate rejection region for testing in the given situation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
67
A paired difference experiment yielded pairs of observations. For the given case, what is the rejection region for testing against Ha: ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
68
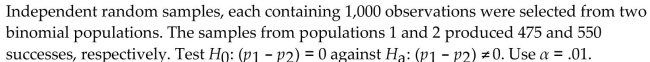

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
69
Which of the following represents the difference in two population means?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
70
A consumer protection agency is comparing the work of two electrical contractors. The agency plans to inspect residences in which each of these contractors has done the wiring in order toestimate the difference in the proportions of residences that are electrically deficient. Suppose the proportions of residences with deficient work are expected to be about .1 for both contractors. How many homes should be sampled in order to estimate the difference in proportions using a 90% confidence interval of width .1?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
71
Using paired differences removes sources of variation that tend to inflate 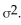

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
72
An experiment has been conducted at a university to compare the mean number of study hours expended per week by student athletes with the mean number of hours expended by non athletes. A random sample of 55 athletes produced a mean equal to 20.6 hours studied per week and a standard deviation equal to 5.8 hours. A second random sample of 200 non athletes produced a mean equal to 23.5 hours per week and a standard deviation equal to 4.6 hours. How many students would need to be sampled in order to estimate the difference in means to within 1.5 hours with probability 95%?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
73
A paired difference experiment yielded pairs of observations. For the given case, what is the rejection region for testing against Ha: ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
74


Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
75
Which of the following represents the ratio of variances?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
76
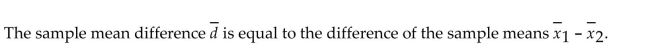

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
77
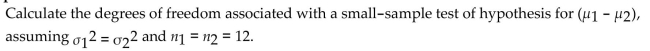
A) 11
B) 23
C) 12
D) 25

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the following set of salary data: 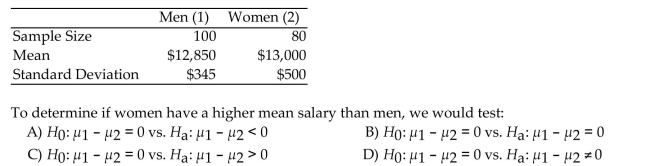
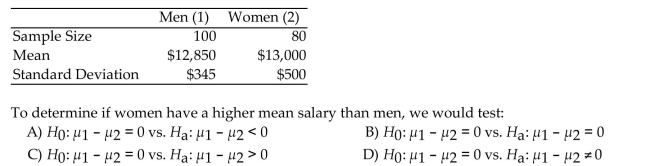

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
79
Data was collected from CEOs of companies within both the low-tech industry and the consumer products industry. The following printout compares the mean return-to-pay ratios between CEOs in the low tech industry with CEOs in the consumer products industry.
HYPOTHESIS: MEAN X = MEAN
industry1
industry3
SAMPLE MEAN OF
SAMPLE VARIANCE OF
SAMPLE SIZE OF
SAMPLE MEAN OF
SAMPLE VARIANCE OF
SAMPLE SIZE OF
MEAN X - MEAN Y
SD. ERROR
If we conclude that the mean return-to-pay ratios of the consumer products and low tech CEOs are
Equal when, in fact, a difference really does exist between the means, we would be making a__________.
A) Type I error
B) correct decision
C) Type II error
D) Type III error
HYPOTHESIS: MEAN X = MEAN
industry1
industry3
SAMPLE MEAN OF
SAMPLE VARIANCE OF
SAMPLE SIZE OF
SAMPLE MEAN OF
SAMPLE VARIANCE OF
SAMPLE SIZE OF
MEAN X - MEAN Y
SD. ERROR
If we conclude that the mean return-to-pay ratios of the consumer products and low tech CEOs are
Equal when, in fact, a difference really does exist between the means, we would be making a__________.
A) Type I error
B) correct decision
C) Type II error
D) Type III error

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
80
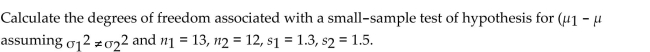
A) 23
B) 11
C) 25
D) 12

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck


