Deck 15: Nonparametric Statistics Available on CD
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 15: Nonparametric Statistics Available on CD
1
Independent random samples from two populations are shown below.
Sample A: 11, 15, 18, 21
Sample B: 9, 12, 15, 17, 20, 23
Calculate the rank sum for each sample. Which would be used as the test statistic in a Wilcoxon rank sum test?
Sample A: 11, 15, 18, 21
Sample B: 9, 12, 15, 17, 20, 23
Calculate the rank sum for each sample. Which would be used as the test statistic in a Wilcoxon rank sum test?
Population A:
Population B:
The test statistic is since it corresponds to the smaller sample.
Population B:
The test statistic is since it corresponds to the smaller sample.
2
The median household income of a community is reported to be $62,000. A random sample of six households in the community yielded the following incomes.
Does the sample provide sufficient evidence to refute the reported median household income? Perform a sign test using .
Does the sample provide sufficient evidence to refute the reported median household income? Perform a sign test using .
versus -value ; Since the -value is not less than , we do not reject the null hypothesis. There is insufficient evidence to refute the reported median income of .
3
A technician is interested in comparing the time it takes to assemble a certain computer component using three different machines. Workers are randomly selected and randomly assigned to one of the machines. The assembly times (in minutes) are shown in the table.
Use the Kruskal-Wallis H-test to test whether the distributions of assembly times differ for the three different machines. Be sure to specify the null and alternative hypotheses. Use
Use the Kruskal-Wallis H-test to test whether the distributions of assembly times differ for the three different machines. Be sure to specify the null and alternative hypotheses. Use
: The distributions of assembly times are the same for the three different machines
: At least two of the three machines have assembly time distributions that differ in location
Critical value ; test statistic ; reject
There is enough evidence to conclude that at least two of the three machines have assembly time distributions that differ in location.
: At least two of the three machines have assembly time distributions that differ in location
Critical value ; test statistic ; reject
There is enough evidence to conclude that at least two of the three machines have assembly time distributions that differ in location.
4
A pharmaceutical company wishes to test a new drug with the expectation of lowering cholesterol levels. Ten subjects are randomly selected and their cholesterol levels are recorded. The results are listed below. The subjects were placed on the drug for a period of 6 months, after which their cholesterol levels were tested again. The results are listed below. (All units are milligrams per deciliter.) Use the Wilcoxon signed rank test to test the company's claim that the drug lowers cholesterol level

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
Independent random samples from two populations are shown below.
Sample A: 35, 38, 42, 43, 45, 47, 49, 58
Sample B: 36, 41, 44, 53, 57
Calculate the rank sum for each sample. Which would be used as the test statistic in a Wilcoxon rank sum test?
Sample A: 35, 38, 42, 43, 45, 47, 49, 58
Sample B: 36, 41, 44, 53, 57
Calculate the rank sum for each sample. Which would be used as the test statistic in a Wilcoxon rank sum test?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
A physician claims that a person's diastolic blood pressure can be lowered, if, instead of taking a drug, the person listens to a relaxation tape each evening. Ten subjects are randomly selected. Their blood pressures, measured in millimeters of mercury, are listed below. The 10 patients are given the tapes and told to listen to them each evening for one month. At the end of the month, their blood pressures are taken again. The data are listed below. Use the Wilcoxon signed rank test to test the physician's claim. Use ? = 0.05.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
Specify the rejection region for the Wilcoxon rank sum test in the following situation.
: Two probability distributions, 1 and 2 , are identical
: Probability distribution of population 1 is shifted to the right of the probability distribution for population 2
: Two probability distributions, 1 and 2 , are identical
: Probability distribution of population 1 is shifted to the right of the probability distribution for population 2

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
The final exam scores of 10 randomly selected statistics students and the number of hours they studied for the exam are given below. Calculate Spearman's rank correlation coefficient. Can you conclude that there is a correlation between the scores on the test and the times spent studying?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
Fading of wood is a problem with wooden decks on boats. Three varnishes used to retard this aging process were tested to see whether there were any differences among them.
Samples of 10 different types of wood were treated with each of the three varnishes and the amount of fading was measured after three months of exposure to the sun. The data are listed below. Is there evidence of a difference in the probability distributions of the amounts of fading for the three different types of varnish? Apply the Friedman Fr-test to the data. Be sure to specify the null and alternative hypotheses.
Samples of 10 different types of wood were treated with each of the three varnishes and the amount of fading was measured after three months of exposure to the sun. The data are listed below. Is there evidence of a difference in the probability distributions of the amounts of fading for the three different types of varnish? Apply the Friedman Fr-test to the data. Be sure to specify the null and alternative hypotheses.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
A government agency claims that the median hourly wages for workers at fast food restaurants in the western U.S. is $6.35. In a random sample of 100 workers, 68 were paid less than $6.35, 10 were paid $6.35, and the rest more than $6.35. Test the government's claim.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
A medical researcher wishes to try three different techniques to lower blood pressure of patients with high blood pressure. The subjects are randomly selected and assigned to one of three groups. Group 1 is given medication, Group 2 is assigned an exercise program and Group 3 is assigned a dietary regimen. At the end of six weeks, the reduction in each subject's blood pressure is recorded. The results (in ) are shown in the table. Use the Kruskal-Wallis H-test to test whether the distributions of the blood pressure reductions differ among the three groups. Be sure to specify the null and alternative hypotheses. Use .

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
A convenience store owner believes that the median number of lottery tickets sold per day is 54. The lottery company believes the median number is smaller. A random sample of 20 days yields the following data. Test the lottery company's claim. Use ? = 0.05.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
Six patients were each given four different pain killers and asked to rate each pain killer's effectiveness in reducing pain on a scale of 1 to 10. A Friedman test was performed on the results. A printout is shown below.
Friedman Test: Response versus Treatment blocked by Patient
Grand median Is there evidence that at least two of the treatment probability distributions differ in location? Explain.
Friedman Test: Response versus Treatment blocked by Patient
Grand median Is there evidence that at least two of the treatment probability distributions differ in location? Explain.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
A researcher wants to know if the time spent in prison for a particular type of crime is the same for men and women. A random sample of men and women were each asked to give the length of sentence received. The data, in months, are listed below. Use the Wilcoxon rank sum procedure to test the claim that there is no difference in the sentences received by men and the sentences received by women. Use ? = 0.05.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
A weight-lifting coach claims that a weight-lifter can increase strength by taking vitamin E. To test the theory, the coach randomly selects 9 athletes and gives them a strength test using a bench press. Thirty days later, after regular training supplemented by vitamin E, they are given the same test again. The weights pressed (in pounds) before and after the vitamin E regimen are shown below. Use the Wilcoxon signed rank test to test the claim that the vitamin E supplement is effective in increasing the athletes' strength. Use ? = 0.05.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
Nine students took the SAT test. Later, they took a test preparation course and retook the SAT. Their original scores and new scores are shown below. Use the Wilcoxon signed rank test to test the claim that the test preparation had an effect on their scores.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
The drama department at a college asked professors and students in the drama department to rank 8 actors according to their performance. The data are listed below. A 10 is the highest ranking and a 1 the lowest ranking. Calculate Spearman's rank correlation coefficient. Test the claim of no correlation between the rankings. Be sure to specify the null and alternative hypotheses

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
Specify the rejection region for the Wilcoxon signed rank test in the following situation.
: Two probability distributions, 1 and 2, are identical
: Probability distribution of population 1 is shifted to the right of the probability distribution for population 2
: Two probability distributions, 1 and 2, are identical
: Probability distribution of population 1 is shifted to the right of the probability distribution for population 2

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
A consumer protection organization claims that a new car model gets less than 25 miles per gallon of gas. Ten cars are tested. The results are given below. Test the organization's claim.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
The table below lists the verbal and math SAT scores of 10 students selected at random.
Calculate Spearman's rank correlation coefficient. Test the hypothesis of no correlation between verbal and math SAT scores. Be sure to specify the null and alternative hypotheses. Use
Calculate Spearman's rank correlation coefficient. Test the hypothesis of no correlation between verbal and math SAT scores. Be sure to specify the null and alternative hypotheses. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
The temperatures on randomly chosen days during a summer class and the number of absences from class on those days are listed below. Calculate Spearman's rank correlation coefficient. Can you conclude that there is a correlation between the temperature and the number absent? Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
What are rank statistics (or rank tests)?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
A local school district is concerned about the number of school days missed by its teachers due to illness. A random sample of 10 teachers is selected. An incentive program is offered in an attempt to reduce absences. The number of days of absence in the year before the incentive program and in the year after the incentive program are shown below for each teacher. Use the Wilcoxon signed rank test to test the claim that the incentive program is effective in reducing absences. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
A researcher wishes to determine whether physical exercise is effective in helping people to lose weight. 20 people were randomly selected to participate in an exercise program for 30 days. Use the Wilcoxon signed rank test to test the claim that exercise has an effect on weight. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
Four different types of fertilizers are used on raspberry plants. The number of raspberries on each of 24 randomly selected plants is given below. Use the Kruskal-Wallis H-test to test whether the distributions of the numbers of raspberries differ among the four groups.
Be sure to specify the null and alternative hypotheses. Use
Be sure to specify the null and alternative hypotheses. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
Specify the rejection region for the Wilcoxon rank sum test in the following situation.
: Two probability distributions, 1 and 2 , are identical
: Probability distribution of population 1 is shifted to the right or left of the probability distribution for population 2
: Two probability distributions, 1 and 2 , are identical
: Probability distribution of population 1 is shifted to the right or left of the probability distribution for population 2

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
Calculate or use a table to find the binomial probability P(x 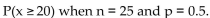 Also use the normal approximation to calculate the probability.
Also use the normal approximation to calculate the probability.
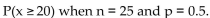 Also use the normal approximation to calculate the probability.
Also use the normal approximation to calculate the probability.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
A researcher wishes to determine whether there is a difference in the average age of elementary school, high school, and community college teachers. Teachers are randomly selected. Their ages are recorded below. Use the Kruskal-Wallis H-test to test whether the distributions of the ages of teachers differ among the three types of school. Be sure to specify the null and alternative hypotheses.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
Test the hypothesis that the median age of statistics teachers is 56 years. A random sample of 60 statistics teachers found 25 above 56 years and 35 below 56 years.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
The ages and systolic blood pressures (measured in millimeters of mercury) of 9 randomly selected adults are given below. Calculate Spearman's rank correlation coefficient. Can you conclude that there is a correlation between age and blood pressure? Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose you have used a randomized block design to compare the effects of four different energy drinks on running speeds. Eight athletes were randomly selected. Each Monday each athlete was assigned an energy drink and their time to run four miles was recorded.
The results (in seconds) are shown below. Is there evidence of a difference in the probability distributions of the running times among the four different drinks? Apply the Friedman Fr-test to the data. Be sure to specify the null and alternative hypotheses. Use
The results (in seconds) are shown below. Is there evidence of a difference in the probability distributions of the running times among the four different drinks? Apply the Friedman Fr-test to the data. Be sure to specify the null and alternative hypotheses. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
Verbal SAT scores for students randomly selected from two different schools are listed below. Use the Wilcoxon rank sum procedure to test the claim that there is no difference in the scores from the two schools. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
The number of absences and the final grades of 9 randomly selected students from a statistics class are given below. Calculate Spearman's rank correlation coefficient. Can you conclude that there is a correlation between the final grade and the number of absences?
Use
Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
What is referred to as nonparametrics?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
Specify the rejection region for the Wilcoxon signed rank test in the following situation.
: Two probability distributions, 1 and 2, are identical
: Probability distribution of population 1 is shifted to the right or left of the probability
: Two probability distributions, 1 and 2, are identical
: Probability distribution of population 1 is shifted to the right or left of the probability

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose you have used a randomized block design to compare the efficacy of three different doses of an experimental drug. You used seven patients in your study. The data are listed below. Do the data indicate that a particular dosage is more effective than other dosages? Apply the Friedman Fr-test to the data. Be sure to specify the null and alternative
hypotheses. Use
hypotheses. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
A realtor wishes to compare the square footage of houses of similar prices in 4 different cities. The data are listed below. Use the Kruskal-Wallis H-test to test whether the square-footage distributions differ for the four different cities. Be sure to specify the null and alternative hypotheses. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
The grade point averages of students participating in different sports at a college are to be compared. The GPAs of students randomly selected from three different groups are listed below. Use the Kruskal-Wallis H-test to test whether the distributions of GPAs differ among the three groups. Be sure to specify the null and alternative hypotheses. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
The Wilcoxon rank sum test is recommended for comparing discrete distributions.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
For a sign test to be valid, a large sample must be selected from a population which is approximately normally distributed.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
The Wilcoxon rank sum test is used to test the hypothesis that the probability distributions associated with two populations are equivalent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
The sign test provides inferences about the population median rather than the population mean.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
Independent random samples from two populations are shown in the table.
Use the Wilcoxon rank sum test to determine whether the data provide sufficient evidence to indicate a shift in the locations of the probability distributions of the sampled populations. Use
Use the Wilcoxon rank sum test to determine whether the data provide sufficient evidence to indicate a shift in the locations of the probability distributions of the sampled populations. Use

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
When applying the Wilcoxon signed rank test, the number of ties should be small relative to the number of observations to ensure the validity of the test.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
The Wilcoxon signed rank test for large samples can be used when n ≥ 10.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
What are distribution-free tests?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose you want to compare two treatments, A and B. In particular, you wish to determine whether the distribution for population B is shifted to the right of the distribution for population A. You plan to use the Wilcoxon rank sum test.
a. Specify the null and alternative hypotheses you would test.
b. Suppose you obtained the following independent random samples of observations on experimental units subjected to the two treatments. Conduct the test of hypotheses described above, using
Sample A: 1.2, 1.5, 2.3, 3.2, 3.7, 4.1
Sample B: 2.5, 2.8, 3.6, 4.2, 4.5
a. Specify the null and alternative hypotheses you would test.
b. Suppose you obtained the following independent random samples of observations on experimental units subjected to the two treatments. Conduct the test of hypotheses described above, using
Sample A: 1.2, 1.5, 2.3, 3.2, 3.7, 4.1
Sample B: 2.5, 2.8, 3.6, 4.2, 4.5

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


